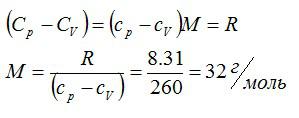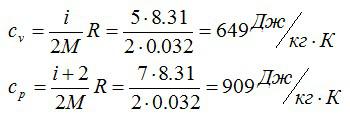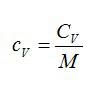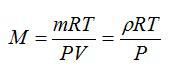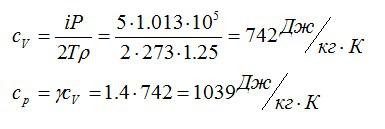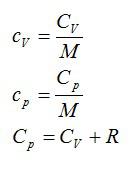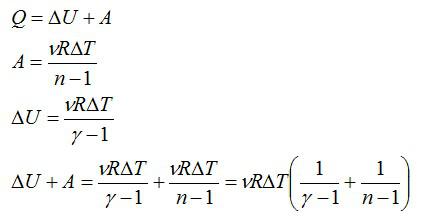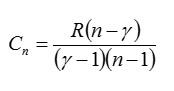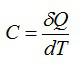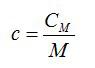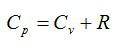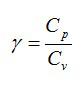From Wikipedia, the free encyclopedia
| Gas | Temp. [°C] | γ |
|---|---|---|
| H2 | −181 | 1.597 |
| −76 | 1.453 | |
| 20 | 1.410 | |
| 100 | 1.404 | |
| 400 | 1.387 | |
| 1000 | 1.358 | |
| 2000 | 1.318 | |
| He | 20 | 1.660 |
| Ar | −180 | 1.760 |
| 20 | 1.670 | |
| O2 | −181 | 1.450 |
| −76 | 1.415 | |
| 20 | 1.400 | |
| 100 | 1.399 | |
| 200 | 1.397 | |
| 400 | 1.394 | |
| N2 | −181 | 1.470 |
| Cl2 | 20 | 1.340 |
| Ne | 19 | 1.640 |
| Xe | 19 | 1.660 |
| Kr | 19 | 1.680 |
| Hg | 360 | 1.670 |
| H2O | 20 | 1.330 |
| 100 | 1.324 | |
| 200 | 1.310 | |
| CO2 | 0 | 1.310 |
| 20 | 1.300 | |
| 100 | 1.281 | |
| 400 | 1.235 | |
| 1000 | 1.195 | |
| CO | 20 | 1.400 |
| NO | 20 | 1.400 |
| N2O | 20 | 1.310 |
| CH4 | −115 | 1.410 |
| −74 | 1.350 | |
| 20 | 1.320 | |
| NH3 | 15 | 1.310 |
| SO2 | 15 | 1.290 |
| C2H6 | 15 | 1.220 |
| C3H8 | 16 | 1.130 |
| Dry air | -15 | 1.404 |
| 0 | 1.403 | |
| 20 | 1.400 | |
| 100 | 1.401 | |
| 200 | 1.398 | |
| 400 | 1.393 | |
| 1000 | 1.365 |
In thermal physics and thermodynamics, the heat capacity ratio, also known as the adiabatic index, the ratio of specific heats, or Laplace’s coefficient, is the ratio of the heat capacity at constant pressure (CP) to heat capacity at constant volume (CV). It is sometimes also known as the isentropic expansion factor and is denoted by γ (gamma) for an ideal gas[note 1] or κ (kappa), the isentropic exponent for a real gas. The symbol γ is used by aerospace and chemical engineers.
where C is the heat capacity, 
The heat capacity ratio is important for its applications in thermodynamical reversible processes, especially involving ideal gases; the speed of sound depends on this factor.
To understand this relation, consider the following thought experiment. A closed pneumatic cylinder contains air. The piston is locked. The pressure inside is equal to atmospheric pressure. This cylinder is heated to a certain target temperature. Since the piston cannot move, the volume is constant. The temperature and pressure will rise. When the target temperature is reached, the heating is stopped. The amount of energy added equals CV ΔT, with ΔT representing the change in temperature. The piston is now freed and moves outwards, stopping as the pressure inside the chamber reaches atmospheric pressure. We assume the expansion occurs without exchange of heat (adiabatic expansion). Doing this work, air inside the cylinder will cool to below the target temperature. To return to the target temperature (still with a free piston), the air must be heated, but is no longer under constant volume, since the piston is free to move as the gas is reheated. This extra heat amounts to about 40% more than the previous amount added. In this example, the amount of heat added with a locked piston is proportional to CV, whereas the total amount of heat added is proportional to CP. Therefore, the heat capacity ratio in this example is 1.4.
Another way of understanding the difference between CP and CV is that CP applies if work is done to the system, which causes a change in volume (such as by moving a piston so as to compress the contents of a cylinder), or if work is done by the system, which changes its temperature (such as heating the gas in a cylinder to cause a piston to move). CV applies only if 
Ideal-gas relations[edit]
For an ideal gas, the molar heat capacity is at most a function of temperature, since the internal energy is solely a function of temperature for a closed system, i.e., 
Mayer’s relation allows us to deduce the value of CV from the more easily measured (and more commonly tabulated) value of CP:
This relation may be used to show the heat capacities may be expressed in terms of the heat capacity ratio (γ) and the gas constant (R):
Relation with degrees of freedom[edit]
The classical equipartition theorem predicts that the heat capacity ratio (γ) for an ideal gas can be related to the thermally accessible degrees of freedom (f) of a molecule by
Thus we observe that for a monatomic gas, with 3 translational degrees of freedom per atom:
As an example of this behavior, at 273 K (0 °C) the noble gases He, Ne, and Ar all have nearly the same value of γ, equal to 1.664.
For a diatomic gas, often 5 degrees of freedom are assumed to contribute at room temperature since each molecule has 3 translational and 2 rotational degrees of freedom, and the single vibrational degree of freedom is often not included since vibrations are often not thermally active except at high temperatures, as predicted by quantum statistical mechanics. Thus we have
For example, terrestrial air is primarily made up of diatomic gases (around 78% nitrogen, N2, and 21% oxygen, O2), and at standard conditions it can be considered to be an ideal gas. The above value of 1.4 is highly consistent with the measured adiabatic indices for dry air within a temperature range of 0–200 °C, exhibiting a deviation of only 0.2% (see tabulation above).
For a linear triatomic molecule such as CO2, there are only 5 degrees of freedom (3 translations and 2 rotations), assuming vibrational modes are not excited. However, as mass increases and the frequency of vibrational modes decreases, vibrational degrees of freedom start to enter into the equation at far lower temperatures than is typically the case for diatomic molecules. For example, it requires a far larger temperature to excite the single vibrational mode for H2, for which one quantum of vibration is a fairly large amount of energy, than for the bending or stretching vibrations of CO2.
For a non-linear triatomic gas, such as water vapor, which has 3 translational and 3 rotational degrees of freedom, this model predicts
Real-gas relations[edit]
As noted above, as temperature increases, higher-energy vibrational states become accessible to molecular gases, thus increasing the number of degrees of freedom and lowering γ. Conversely, as the temperature is lowered, rotational degrees of freedom may become unequally partitioned as well. As a result, both CP and CV increase with increasing temperature.
Despite this, if the density is fairly low and intermolecular forces are negligible, the two heat capacities may still continue to differ from each other by a fixed constant (as above, CP = CV + nR), which reflects the relatively constant PV difference in work done during expansion for constant pressure vs. constant volume conditions. Thus, the ratio of the two values, γ, decreases with increasing temperature.
However, when the gas density is sufficiently high and intermolecular forces are important, thermodynamic expressions may sometimes be used to accurately describe the relationship between the two heat capacities, as explained below. Unfortunately the situation can become considerably more complex if the temperature is sufficiently high for molecules to dissociate or carry out other chemical reactions, in which case thermodynamic expressions arising from simple equations of state may not be adequate.
Thermodynamic expressions[edit]
Values based on approximations (particularly CP − CV = nR) are in many cases not sufficiently accurate for practical engineering calculations, such as flow rates through pipes and valves at moderate to high pressures. An experimental value should be used rather than one based on this approximation, where possible. A rigorous value for the ratio CP/CV can also be calculated by determining CV from the residual properties expressed as
Values for CP are readily available and recorded, but values for CV need to be determined via relations such as these. See relations between specific heats for the derivation of the thermodynamic relations between the heat capacities.
The above definition is the approach used to develop rigorous expressions from equations of state (such as Peng–Robinson), which match experimental values so closely that there is little need to develop a database of ratios or CV values. Values can also be determined through finite-difference approximation.
Adiabatic process[edit]
This ratio gives the important relation for an isentropic (quasistatic, reversible, adiabatic process) process of a simple compressible calorically-perfect ideal gas:
is constant
Using the ideal gas law, 
is constant
is constant
where P is the pressure of the gas, V is the volume, and T is the thermodynamic temperature.
In gas dynamics we are interested in the local relations between pressure, density and temperature, rather than considering a fixed quantity of gas. By considering the density 

Since for constant entropy, 


For an imperfect or non-ideal gas, Chandrasekhar[3] defined three different adiabatic indices so that the adiabatic relations can be written in the same form as above; these are used in the theory of stellar structure:
All of these are equal to 
See also[edit]
- Relations between heat capacities
- Heat capacity
- Specific heat capacity
- Speed of sound
- Thermodynamic equations
- Thermodynamics
- Volumetric heat capacity
References[edit]
- ^ White, Frank M. (October 1998). Fluid Mechanics (4th ed.). New York: McGraw Hill. ISBN 978-0-07-228192-7.
- ^ Lange, Norbert A. (1967). Lange’s Handbook of Chemistry (10th ed.). New York: McGraw Hill. p. 1524. ISBN 978-0-07-036261-1.
- ^ Chandrasekhar, S. (1939). An Introduction to the Study of Stellar Structure. Chicago: University of Chicago Press. p. 56. ISBN 978-0-486-60413-8.
Notes[edit]
- ^ γ first appeared in an article by the French mathematician, engineer, and physicist Siméon Denis Poisson:
- Poisson (1808). «Mémoire sur la théorie du son» [Memoir on the theory of sound]. Journal de l’École Polytechnique (in French). 7 (14): 319–392. On p. 332, Poisson defines γ merely as a small deviation from equilibrium which causes small variations of the equilibrium value of the density ρ.
In Poisson’s article of 1823 –
- Poisson (1823). «Sur la vitesse du son» [On the speed of sound]. Annales de chimie et de physique. 2nd series (in French). 23: 5–16.
γ was expressed as a function of density D (p.
or of pressure P (p. 9).
Meanwhile, in 1816 the French mathematician and physicist Pierre-Simon Laplace had found that the speed of sound depends on the ratio of the specific heats.- Laplace (1816). «Sur la vitesse du son dans l’air et dans l’eau» [On the speed of sound in air and in water]. Annales de chimie et de physique. 2nd series (in French). 3: 238–241.
However, he didn’t denote the ratio as γ.
In 1825, Laplace stated that the speed of sound is proportional to the square root of the ratio of the specific heats:- Laplace, P.S. (1825). Traité de mecanique celeste [Treatise on celestial mechanics] (in French). Vol. 5. Paris, France: Bachelier. pp. 127–137. On p. 127, Laplace defines the symbols for the specific heats, and on p. 137 (at the bottom of the page), Laplace presents the equation for the speed of sound in a perfect gas.
In 1851, the Scottish mechanical engineer William Rankine showed that the speed of sound is proportional to the square root of Poisson’s γ:
- Rankine, William John Macquorn (1851). «On Laplace’s Theory of Sound«. Philosophical Magazine. 4th series. 1 (3): 225–227.
It follows that Poisson’s γ is the ratio of the specific heats — although Rankine didn’t state that explicitly.
- See also: Krehl, Peter O. K. (2009). History of Shock Waves, Explosions and Impact: A Chronological and Biographical Reference. Berlin and Heidelberg, Germany: Springer Verlag. p. 276. ISBN 9783540304210.
Определение отношения теплоемкостей
Газов (Ср / сv) способом дезорма и клемана
Цель работы: определить отношение теплоемкостей (Ср/сv) для воздуха.
Приборы
и принадлежности:
стеклянные баллоны, U-образный
водяной манометр, ручной насос.
Краткое теоретическое введение
Теплоемкостью
называется количество теплоты, которое
необходимо сообщить телу для изменения
его температуры на 1 К.
Теплоемкость,
отнесенная к единице массы вещества,
называется удельной теплоемкостью, а
отношение к молю – молярной, или мольной
теплоемкостью.
По определению
теплоемкость
.
(1)
Газ,
получая (или отдавая) тепло, изменяет
свой объем и совершает работу, а также
изменяет свою внутреннюю энергию.
По первому началу
термодинамики
dQ
= dU
+ dA,
(2)
dQ
– теплота, переданная газу; dU
– изменение
внутренней энергии газа; dA
– работа,
совершаемая газом.
Элементарная
работа, совершаемая газом при изменении
его объема, определяется
dA
= РdV, (3)
Р
– давление
газа; dV
– изменение объема.
Теплоемкость
газа найдем, используя уравнения (1) и
(2).
,
(4)
или
.
(4, а)
Так
как давление Р
зависит от объема V
по-разному в зависимости от процесса,
то теплоемкость для различных процессов
будет неодинакова.
При
изохорном процессе V
=
const,
dV = 0 (dA
= 0), а поэтому теплоемкость газа,
сохраняющего неизменным объем,
.
(5)
При
изобарном процессе остается неизменным
давление газа, т.е. Р
= const. Величину
PdV
найдем, используя уравнение
Менделеева–Клапейрона
PV
= RT.
Продифференцируем уравнение (6) для случая
P = const
(6)
PdV
= RdT.
(7)
Таким
образом, теплоемкость газа при постоянном
давлении определяется из уравнения (4,
а)
.
(8)
Из
уравнения (8) видно, что всегда СР
>
СV.
Непосредственное определение теплоемкостей
довольно затруднительно, особенно СV.
Однако во многих задачах определяют
отношение теплоемкости при постоянном
давлении (СР)
к теплоемкости при постоянном объеме
(СV)
.
(9)
Величина
этого отношения одинакова как для
молярных, так и для удельных теплоемкостей,
так как
,
где
– молярные теплоемкости, а
– удельные теплоемкости газа при
постоянном давлении и объеме,
соответственно,
– молярная масса газа.
Отношение
удельных теплоемкостей газов играет
очень большую роль при адиабатических
процессах и при процессах, близких к
ним.
Величиной
определяется, например, скорость
распространения звука в газах, от нее
зависит течение газов по трубам со
звуковыми скоростями и достижения
сверхзвуковых скоростей в расширяющихся
трубах.
Адиабатический
процесс – это процесс, протекающий без
теплообмена с окружающей средой. Можно
с достаточным приближением рассматривать
всякое быстрое изменение объема как
процесс адиабатный и чем быстрее он
происходит, тем ближе к адиабатному.
Применим первое
начало термодинамики к адиабатному
процессу
dQ
=
0,
dA + dU
= 0 или
dA = dU,
т.е. при адиабатном
процессе работа совершается газом,
только за счет изменения внутренней
энергии.
Выразим
dU
из уравнения (5), тогда работа газа при
адиабатном расширении будет иметь вид
dA
= CV
dT.
(10)
Используя
уравнения (5), (7), (8) и (9), можно получить
связь между давлением и объемом при
адиабатном процессе
PV
=const (уравнение
Пуассона), (11)
где
= СР/CV
–
показатель адиабаты.
Показатель
адиабаты для одноатомного, двухатомного
и многоатомного газа будет разным.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Перевод термодинамической системы (например, порции идеального газа) из состояния `1` в состояние `2` можно осуществить разными способами. На рис. 12 показаны графики двух возможных процессов (`1-«а»-2` и `1-«в»-2`), позволяющих осуществить такой перевод. Изменение внутренней энергии системы в том и в другом случае одинаково (оно определяется положениями точек `1` и `2` на -диаграмме), а работа, совершённая системой над окружающими телами, различна (площадь фигур под графиками процессов `1-«а»-2` и `1-«в»-2` разная, площадь под графиком процесса `1-«в»-2` больше).
Следовательно, и количество теплоты, затраченное на перевод системы из состояния `1` в `2` ( $$ Q=Delta U+{A}^{text{‘}}$$ ), будет разным.
Теплоёмкостью $$ C$$ термодинамической системы (тела) называют отношение бесконечно малого количества теплоты $$ Delta Q$$, переданного системе, к изменению $$ Delta T$$ его температуры, вызванного этим количеством теплоты.
$$ C={displaystyle frac{Delta Q}{Delta T}}$$ — теплоёмкость тела (системы).
Единицей измерения этой величины будет $$ left[Cright]={displaystyle frac{1mathrm{Дж}}{mathrm{К}}}$$.
Численное значение теплоёмкости тела показывает, какое количество теплоты потребуется для изменения температуры всего тела на `1` градус по шкале Цельсия (Кельвина).
При расчётах чаще пользуются удельной теплоёмкостью (теплоёмкостью `1` кг вещества).
называют отношение теплоёмкости тела (системы) к массе этого тела (системы):
| $$ {c}_{mathrm{уд}}={displaystyle frac{C}{m}}={displaystyle frac{Delta Q}{m· Delta T}}$$ — удельная теплоёмкость тела (системы). | (1) |
Единицей измерения этой величины будет $$ left[cright]={displaystyle frac{1mathrm{Дж}}{mathrm{кг}·mathrm{К}}}$$.
называют отношение теплоёмкости тела (системы) к количеству вещества в этом теле (системе):
| $$ {c}_{mathrm{мол}}={displaystyle frac{C}{nu }}={displaystyle frac{Delta Q}{ Delta T·nu }}$$ — молярная теплоёмкость тела (системы). | (2) |
Единицей измерения этой величины будет $$ left[{c}_{mathrm{мол}}right]={displaystyle frac{1mathrm{Дж}}{mathrm{моль}·mathrm{К}}}$$.
Получим соотношение между удельной и молярной теплоёмкостями:
| $$ {c}_{mathrm{мол}}={displaystyle frac{Q}{ Delta T·frac{m}{M}}}={displaystyle frac{Q·M}{ Delta T·m}}={c}_{mathrm{уд}}·M$$ — соотношение между молярной и удельной теплоёмкостями | (3) |
Теперь найдём молярную теплоёмкость идеального газа при изобарном и при изохорном процессах.
При изобарном процессе присутствуют и $$ Delta U$$, и $$ {A}^{text{‘}}$$, следовательно:
$$ {c}_{p}={displaystyle frac{Q}{nu · Delta T}}={displaystyle frac{Delta U+Atext{‘}}{nu · Delta T}}={displaystyle frac{Delta U}{nu Delta T}}+{displaystyle frac{Atext{‘}}{nu Delta T}}={displaystyle frac{frac{i}{2}nu R Delta T}{nu Delta T}}+{displaystyle frac{nu R Delta T}{nu Delta T}}={displaystyle frac{iR}{2}}+R=R{displaystyle frac{i+2}{2}}$$,
$${c}_{p}=R{displaystyle frac{i+2}{2}}$$ — молярная теплоёмкость газа при изобарном процессе.
При изохорном процессе работа не совершается, $$ {A}^{text{‘}}=0$$, следовательно:
$$ {c}_{V}={displaystyle frac{Q}{nu Delta T}}={displaystyle frac{Delta U+{A}^{text{‘}}}{nu Delta T}}={displaystyle frac{Delta U}{nu Delta T}}={displaystyle frac{frac{i}{2}nu R Delta T}{nu Delta T}}={displaystyle frac{iR}{2}}$$
$$ {c}_{V}=R{displaystyle frac{i}{2}}$$ — молярная теплоёмкость газа при изохорном процессе.
Соотношение между $$ {c}_{V}$$ и $$ {c}_{р}$$ можно записать в двух формах:
1) $$ {c}_{p}={c}_{V}+R$$ — закон Майера, и
2) $$ gamma ={displaystyle frac{{c}_{p}}{{c}_{V}}}$$ — коэффициент Пуассона.
Т. к. мы уже знаем, чему равно число степеней свободы у разных молекул, то можем вычислить и значения $$ {с}_{р}$$ и $$ gamma $$:
|
формула |
Одноатомные `(i = 3)` |
Двухатомные `(i = 5)` |
|||
| `c_p` |
`R((i+2)/2)` |
`5/2 R` |
`20,775 «Дж»/(«моль»*»К»)` | `7/2 R` | `29,085 «Дж»/(«моль»*»К»)` |
|
`gamma` |
`(i+2)/i` |
`5/3` |
`1,66667` |
`7/5` |
`1,4` |
Воздух представляет собой смесь газов, преимущественно двухатомных азота и кислорода, потому для него эксперименты дают значение $$ gamma approx mathrm{1,4}$$.
Для твёрдых тел теплоёмкости $$ {с}_{р}$$ и $$ {c}_{V}$$ будут почти одинаковыми. Это можно показать следующим образом. По определению $$ C={displaystyle frac{Delta Q}{ Delta T}}$$, но $$ Delta Q= Delta U+pDelta V$$, тогда
$$ {C}_{p}={displaystyle frac{Delta U+pDelta V}{ Delta T}}={displaystyle frac{Delta U}{ Delta T}}+{displaystyle frac{pDelta V}{ Delta T}}={C}_{V}+{displaystyle frac{pDelta V}{ Delta T}}$$.
При нагревании твёрдых или жидких тел изменение объёма составляет около $$ {10}^{-6}$$ первоначального объёма, поэтому вторым слагаемым можно пренебречь по сравнению с первым, что и позволяет говорить о равенстве $$ {c}_{p}={c}_{V}$$.
Для газов $$ frac{ Delta V}{V}$$ на два порядка больше, чем для твёрдых или жидких тел, потому пренебрегать вторым слагаемым нельзя, более того, оно будет составлять заметную долю теплоёмкости $$ {c}_{p}$$.
Решение задач дело полезное, но не всегда интересное. Чтобы вы справлялись с решением задач по теме «Теплоемкость идеального газа» быстрее, приведем здесь несколько примеров и вопросов с объяснениями.
Подписывайтесь на наш телеграм-канал, чтобы получать полезную и интересную рассылку.
Задачи по теме «Теплоемкость идеального газа» с решениями
Повторение и практика – залог успеха в любом деле. И решение задач не исключение. Поэтому не забываем держать под рукой памятку по задачам и полезные формулы
Задача №1. Определить удельную теплоемкость идеального газа
Условие
Определить молярную массу M двухатомного газа и его удельные теплоемкости, если известно, что разность cр — cv удельных теплоемкостей этого газа равна 260 Дж/(кг*К)
Решение
По определению:
Значит, газ из задачи – кислород. Если кто не понял, как это определяется, учитесь пользоваться таблицей Менделеева.
Считаем удельные теплоемкости:
Ответ: 32 г/моль; 649 Дж/кг*К; 909 Дж/кг*К.
Задача №2. Удельная теплоемкость
Условие
Плотность некоторого газа при нормальных условиях ρ = 1,25 кг/м3. Отношение удельных теплоемкостей γ = 1,4. Определить удельные теплоемкости cv и сp этого газа.
Решение
Исходя из отношения удельных теплоемкостей, можно сделать вывод, что газ – двухатомный, i=5. При постоянном объеме удельная теплоемкость равна:
Молярную массу можно найти из уравнения Клапейрона-Менделеева:
Отсюда:
Ответ: 742 Дж/кг*К; 1039 Дж/кг*К.
Задача №3. Молярная теплоемкость
Условие
Вычислить молярные теплоемкости газа, зная, что его молярная масса М = 4∙10 3 кг/моль и отношение удельных теплоемкостей ср/сv = 1,67.
Решение
Удельные теплоемкости равны:
Можно найти:
Ответ: 12,4 Дж/моль*К; 20,71 Дж/моль*К
Задача №4. Теплоемкость при изопроцессах
Условие
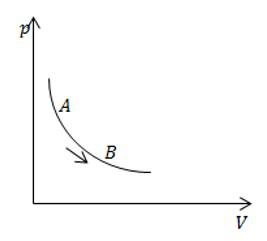
На рисунке изображен изотермический процесс с газом постоянной массы. Сравните теплоемкость в процессе АВ с теплоемкостью этой же массы газа в изохорном процессе.
Решение
Теплоемкость при изохорном процессе является постоянной величиной. При изотермическом процесса она равна бесконечности. Значит, теплоемкость в процессе АВ больше.
Ответ: Теплоемкость в процессе АВ больше.
Задача №5. Теплоемкость при политропическом процессе
Условие
Найдите молярную теплоемкость идеального газа при политропическом процессе pVn = const, если показатель адиабаты газа равен γ. При каких значениях показателя политропы n теплоемкость газа будет отрицательной?
Решение
Запишем первое начало термодинамики, выражения для работы и изменения внутренней энергии в политропическом процессе соответственно:
Если количество вещества и изменение температуры принять равными единице, это выражение будет равно молярной теплоемкости (по определению теплоемкости):
Ответ: см. выражение выше.
Вопросы по теме «Теплоемкость идеального газа»
Вопрос 1. Что такое теплоемкость идеального газа?
Ответ. Когда газу сообщается определенное количество теплоты, меняется его температура.
Отношение количества теплоты, сообщенного газу, к изменению его температуры, называется теплоемкостью идеального газа.
Вопрос 2. Что такое молярная и удельная теплоемкость идеального газа?
Ответ. Молярная и удельная теплоемкости активно используются в термодинамике. Молярная теплоемкость – это теплоемкость одного моля вещества.
Удельная теплоемкость – теплоемкость единичной массы вещества.
Вопрос 3. Как определяется теплоемкость газа при изопроцессах?
Ответ.
При изотермическом процессе T=const. Теплоемкость равна плюс/минус бесконечности.
При адиабатном процессе нет теплообмена с окружающей средой, теплоемкость равна нулю.
При изохорном процессе газ не совершает работы, а теплоемкость равна:
Здесь i – количество степеней свободы молекул газа. Для одноатомных газов i=3, для двухатомных i=5.
При изобарном процессе теплоемкость определяется соотношением Мейера:
Вопрос 4. Как еще связаны теплоемкости при постоянном давлении и постоянном объеме?
Ответ. Отношение теплоемкостей при постоянном давлении и постоянном объеме обозначается греческой буквой «гамма» и называется показателем адиабаты.
Вопрос 5. Как называются процессы, в которых теплоемкость газа остается неизменной?
Ответ. Такие процессы называются политропными. Адиабатный процесс – частный случай политропного процесса.
Теплоемкость реального газа не равна теплоемкости идеального газа и может сильно отличаться.
Нужна помощь в решении задач и выполнении других заданий? Специальный студенческий сервис готов оказать ее!













![{displaystyle {begin{aligned}Gamma _{1}&=left.{frac {partial ln P}{partial ln rho }}right|_{S},\[2pt]{frac {Gamma _{2}-1}{Gamma _{2}}}&=left.{frac {partial ln T}{partial ln P}}right|_{S},\[2pt]Gamma _{3}-1&=left.{frac {partial ln T}{partial ln rho }}right|_{S}.end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7646c0aafdd5e68c49c35bd36abaf2bbefc2149f)
 or of pressure P (p. 9).
or of pressure P (p. 9).