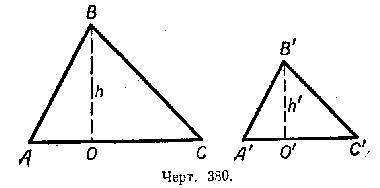ГЛАВА VIII.
ПРОПОРЦИОНАЛЬНОСТЬ ОТРЕЗКОВ. ПОДОБИЕ ФИГУР.
§ 92. ОТНОШЕНИЕ ПЛОЩАДЕЙ ПОДОБНЫХ ФИГУР.
1. Отношение площадей квадратов.
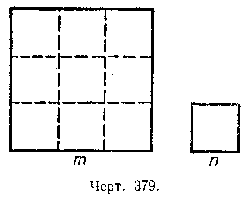
Рассмотрим отношение площадей двух квадратов. Если сторону одного квадрата обозначим через т, а сторону другого — через п, то площади будут соответственно равны
т2 и п2 (черт. 379).
Обозначив площадь первого квадрата через S, а площадь второго через S’, получим: S/S’ = m2/n2 , т. е. площади квадратов относятся как квадраты их сторон.
Полученную формулу можно преобразовать так: S/S’ = ( m/n)2 .
Значит, можно сказать, что отношение площадей двух квадратов равно квадрату отношения их сторон.
На чертеже 379 отношение сторон квадратов равно 3, отношение их площадей равно
32 = 9.
2. Отношение площадей двух подобных треугольников.
Пусть / AВС / A’В’С’ (черт. 380). Из подобия треугольников следует, что
/
A = /
A’ , /
B = /
B’ и /
С = /
С’ . Кроме того, AB/A’B’ = BC/B’C’ = AC/A’C’.
В этих треугольниках из вершин В и В’ проведём высоты и обозначим их через h и h‘. Площадь первого треугольника будет равна AC•h/2, а площадь второго треугольника A’C’•h’/2.
Обозначив площадь первого треугольника через S, а площадь второго — через S’ получим: S/S’ = AC•h/A’C’•h’ или S/S’ = AC/A’C’ • h/h’
Из подобия треугольников АВО и А’В’О’ (они подобны, потому что прямоугольные, и, кроме того, имеют по равному острому углу, а именно /
A = /
A’ ) следует:
h/h’ = AB/A’B’ . Но AB/A’B’ = AC/A’C’ . Следовательно, h/h’ = AC/A’C’. Заменив в формуле S/S’ = AC/A’C’ • h/h’ отношение h/h’ равным ему отношением AC/A’C’ , получим:
S/S’ = AC/A’C’ • AC/A’C’ , или .
Итак, площади подобных треугольников относятся как квадраты сходственных сторон.
Полученную формулу можно преобразовать так: S/S’ = (AC/A’C’ )2.
Значит, можно сказать, что отношение площадей двух подобных треугольников равно квадрату отношения их сходственных сторон.
3. Отношение площадей подобных многоугольников.
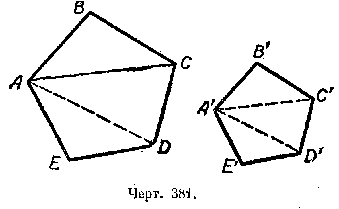
Пусть ABCDE и A’B’C’D’E’ — подобные многоугольники (черт. 381).
Известно, что / AВС / A’В’С’; / ACD
/ A’C’D’ и / ADE
/ A’D’E’ (§90).
Кроме того,
;
Так как вторые отнoшения этих пропорций равны, что вытекает из подобия многоугольников, то
Используя свойство ряда равных отношений получим:
, или
где S и S’ — площади данных подобных многоугольников.
Следовательно, площади подобных многоугольников относятся как квадраты сходственных сторон.
Полученную формулу можно преобразовать к такому виду: S/S’ = (AВ/A’В’ )2
Упражнения.
1. Сторона первого квадрата больше стороны второго квадрата в 2 раза (в 5 раз). Во сколько раз площадь первого квадрата больше площади второго квадрата?
2. Сторона первого квадрата составляет 1/3 (0,1) стороны второго квадрата. Какую часть площадь первого квадрата составляет от площади второго квадрата?
3. Коэффициент подобия в подобных многоугольниках равен 4 (1/5; 0,4; 2,5). Чему равно отношение их площадей?
4. Отношение площадей подобных многоугольников равно 36 (100; 0,09). Чему равно отношение сходственных сторон этих многоугольников?
Сторона одного квадрата равна 12 см, а сторона другого квадрата равна 2 см. Найдите отношение:
1) стороны большого квадрата к стороне малого квадрата;
2) периметра большого квадрата к площади малого квадрата;
3) площади большого квадрата к площади малого квадрата.
Какие из этих отношений равны? Равны ли отношения площадей и сторон квадратов?
reshalka.com
ГДЗ учебник по математике 6 класс Дорофеев. 6.1 Что такое отношение. Номер №480
Решение 1
12 : 2 = 6 : 1 − отношение стороны большого квадрата к стороне малого квадрата.
Ответ: 6 : 1
Решение 2
1) 12 * 4 = 48 (см) − периметр большого квадрата;
2) 2 * 4 = 8 (см) − периметр малого квадрата;
3) 48 : 8 = 6 : 1 − отношение периметра большого квадрата к площади малого квадрата.
Ответ: 6 : 1
Решение 3
1) 12 * 12 = 144
(
с
м
2
)
− площадь большого квадрата;
2) 2 * 2 = 4
(
с
м
2
)
площадь малого квадрата;
3) 144 : 4 = 36 : 1 − отношение площади большого квадрата к площади малого квадрата.
Ответ: 36 : 1
Равны отношения стороны большого квадрата к стороне малого квадрата и отношение периметра большого квадрата к периметру малого квадрата. Отношения площадей и сторон квадратов не равны.
Задача. Сторона квадрата равна (2) дм. Определи, как изменится периметр квадрата, если его сторону увеличить в (3) раза, в (4) раза, в (5) раз?
| Сторона квадрата, дм |
(2) |
(6) |
(8) |
(10) |
| Периметр квадрата, дм |
(8) |
(24) |
(32) |
(40) |
Заметим, что при увеличении стороны квадрата в (3) раза (была (2) дм, стала — (6) дм) периметр увеличился тоже в (3) раза (был (8) дм, стал — (24) дм).
Аналогично, при увеличении стороны квадрата в (4) раза (была (2) дм, стала — (8) дм) периметр увеличился тоже в (4) раза (был (8) дм, стал — (32) дм).
Вывод: при увеличении стороны квадрата в несколько раз периметр увеличивается во столько же раз.
Говорят, что сторона квадрата прямо пропорциональна его периметру.
Две величины называют прямо пропорциональными, если при увеличении (уменьшении) одной из них в несколько раз другая увеличивается (уменьшается) во столько же раз.
Обрати внимание!
Если две величины прямо пропорциональны, то отношения соответствующих значений этих величин равны.
Проверим это утверждение на приведённой выше задаче.
Найдём в каждом случае отношение стороны квадрата к периметру:
Прямую пропорциональность можно задать формулой.
Формулу (y=kx), где (y) и (x) — переменные величины, а (k) — коэффициент, является постоянной величиной, называют формулой прямой пропорциональности.
поделиться знаниями или
запомнить страничку
- Все категории
-
экономические
43,662 -
гуманитарные
33,654 -
юридические
17,917 -
школьный раздел
611,985 -
разное
16,905
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
1. Найдите отношение площадей двух квадратов, если отношение сторон этих квадратов равно : 2 : 3 2.
Как относятся стороны двух квадратов, если отношение площадей этих квадратов равно : 4 : 9 Просьба с объяснением : 3.
Перед вами страница с вопросом 1. Найдите отношение площадей двух квадратов, если отношение сторон этих квадратов равно : 2 : 3 2?, который относится к
категории Геометрия. Уровень сложности соответствует учебной программе для
учащихся 5 — 9 классов. Здесь вы найдете не только правильный ответ, но и
сможете ознакомиться с вариантами пользователей, а также обсудить тему и
выбрать подходящую версию. Если среди найденных ответов не окажется
варианта, полностью раскрывающего тему, воспользуйтесь «умным поиском»,
который откроет все похожие ответы, или создайте собственный вопрос, нажав
кнопку в верхней части страницы.