Чтобы получить точное представление о движении двух объектов относительно друг друга относительная скорость является важным. Поэтому в этой статье мы подробно поговорим об относительной скорости между двумя объектами.
Относительная скорость — это, по сути, скорость одного объекта по отношению к другому. Рассмотрим следующие два объекта, А и В, которые движутся с разными скоростями. Скорость объекта А по отношению к объекту В или наоборот называется относительной скоростью. Он также известен как скорость изменения относительного положения одного объекта по отношению к другому с течением времени.
Как найти относительную скорость двух тел?
🠊 Техника определения скорости объекта требует определения скорости изменения положения объекта по отношению к неподвижному окружающему объекту.
Когда объекты A и B находятся в относительном движении, их соответствующие скорости также будут в относительном движении. Чтобы получить относительную скорость объекта A по отношению к B, нужно математически придать равную и противоположную скорость B как объекту A, так и объекту B, чтобы привести объект B в состояние покоя.
В результате равнодействующая обеих скоростей (скорости объекта А и Б) дает нам относительную скорость объекта А относительно объекта Б.
Уравнения относительной скорости следующие:
Скорость объекта А относительно объекта В можно рассчитать следующим образом:
Vab V =a — Vb
Скорость объекта B относительно объекта A можно рассчитать следующим образом:
Vba V =b — Va
Из двух выражений мы можем вывести следующее:
Vab = — Vba
Однако обе величины равны математически и могут быть представлены как:
|Vab |= |Вba|
Какова относительная скорость между двумя телами, когда они движутся с одинаковой скоростью в одном направлении?
🠊 Когда два тела А и В движутся в одном направлении с одинаковой скоростью, угол между ними равен 0°.
Предположим, что два транспортных средства A и B движутся в одном направлении, т. е. параллельно друг другу, с одинаковой скоростью или скоростью (поскольку они движутся в одном направлении), т. е. Va V =b.
В результате скорость автомобиля А относительно автомобиля В равна:
Vab V =a — Vb = 0
Аналогичным образом, скорость транспортного средства B относительная к транспортному средству А:
Vba V =b — Va = 0
Это означает, что если два объекта двигаться в одном направлении с одинаковой скоростью или скорость, их относительная скорость становится равной нулю. Это демонстрирует, что другой может казаться покоящимся для одного объекта.
Построение графика положение-время для двух объектов, движущихся в одном направлении с одинаковой скоростью, приводит к прямым параллельным линиям, как показано на графике ниже.
Какова относительная скорость между двумя телами, когда они движутся с разными скоростями в одном направлении?
🠊 Если два транспортных средства, A и B, движутся в одном направлении с разными скоростями, в первую очередь следует рассмотреть два сценария:
(1) Начальные точки одинаковы (Va > Vb):
Если два транспортных средства движутся с разными скоростями в одном направлении с одной и той же начальной точкой и Va > Vb, человек в транспортном средстве B воспринимает транспортное средство A как удаляющееся от него со скоростью:
Vab V =a — Vb
Транспортное средство B движется назад к пассажиру в транспортном средстве A со скоростью:
Vba V =b — Va = -( Вa — Vb) = -Vab
В результате обе скорости имеют одинаковую величину, но противоположные знаки.
(2) Различные отправные точки:
Мы можем думать о двух сценариях здесь:
(i) Предположим, что транспортное средство A имеет более высокую скорость, чем транспортное средство B, т. е. Va > Vb, и следует за автомобилем B.
В этой ситуации транспортное средство A в конечном итоге догонит транспортное средство B, как показано на их графике положение-время.
Vab V =a — Vb ≠ 0
(ii) Рассмотрим ситуацию, когда Va > Vb и автомобиль А движется впереди автомобиля В.
В этом случае транспортное средство B никогда не сможет обогнать транспортное средство A.. Графики положения и времени обоих транспортных средств не будут пересекаться по мере их удаления друг от друга.
Vab V =a — Vb ≠ 0
Какова будет относительная скорость двух тел, когда они движутся в противоположных направлениях?
🠊 Угол, образованный двумя телами, движущимися в противоположных направлениях по прямой, называется 180°.
Рассмотрим два автомобиля А и В, движущихся в противоположных направлениях по прямой.
В результате скорость автомобиля А относительно автомобиля В равна:
Vab V =a -(- Вb) = Вa +Vb
Скорость транспортного средства B по отношению к A аналогична:
Vba V =b-(- Вa) = Вa +Vb
В результате можем написать:
Vab V =ba
Это указывает на то, что если два объекта движутся в противоположных направлениях по прямой линии, кажется, что каждый объект движется очень быстро по сравнению с другим.
Какова относительная скорость, когда два тела движутся под углом?
🠊 Рассмотрим пример относительной скорости, который возникает, когда два объекта, A и B, движутся под углом со скоростями Va и Vb.
&
Диагональ даст нам относительную скорость, если мы построим параллелограмм, как показано на рисунке. В результате величина диагонального вектора параллелограмма или относительная скорость с использованием закона косинусов составляет:
Но Cos(180°-𝛳) = -Cos𝛳
Когда два объекта движутся под углом, приведенное выше уравнение дает нам их относительную скорость. Мы также можем вывести случай того же направления и случай противоположного направления из этого уравнения, изменив значение угла на 0° и 180° соответственно.
Однако, как показано на изображении, если вектор относительной скорости Vab образует угол ꞵ со скоростью объекта A, то
Но Sin(180°-𝛳) = Sin𝛳
Или,
Важность относительной скорости:
Важность относительной скорости резюмируется ниже:
- Рассчитать скорость звезд и астероидов относительно Земли.
- Для измерения расстояния между любыми двумя объектами в пространстве.
- Чтобы запустить ракету.
- Для определения скорости любого объекта.
- Это помогает нам, когда объект движется через жидкость.
Проблемы, связанные с относительной скоростью:
1. Автомобиль, едущий по шоссе со скоростью 110 км/ч, проезжает мимо автобуса, идущего со скоростью 85 км/ч. Какова скорость автомобиля с точки зрения пассажира автобуса?
Данный:
Скорость автомобиля Vc = 110 км/ч
Скорость автобуса Vb = 85 км/ч
Найти:
Относительная скорость автомобиля относительно автобуса Vcb знак равно
Решение:
Поскольку автомобиль и автобус едут в одном направлении, относительная скорость автомобиля с точки зрения пассажира автобуса равна:
Vcb V =c — Vb = (110 -85)км/ч = 25 км/ч
Таким образом, скорость автомобиля с точки зрения пассажира автобуса составляет 25 км/ч.
2. Две машины, находящиеся на некотором расстоянии друг от друга, начинают двигаться навстречу друг другу со скоростями 150 м/с и 200 м/с по прямой дороге. С какой скоростью они приближаются друг к другу?
Данный:
Скорость автомобиля 1 В1 = 150 м / с
Скорость автомобиля 2 В2 = 200 м / с
Найти:
Относительная скорость вагона 1 относительно вагона 2 V12 знак равно
Относительная скорость вагона 2 относительно вагона 1 V21 знак равно
Решение:
Так как оба автомобиля едут в противоположном направлении, относительная скорость:
V12 V =1 + V2 = (150 + 200) м/с = 350 м/с
Кроме того,
V21 V =1 + V2 = (150 + 200) м/с = 350 м/с
В результате два автомобиля движутся навстречу друг другу с относительной скоростью 350 м/с.
Резюме:
- Скорость одного объекта по отношению к другому объекту просто называется относительной скоростью этих двух объектов.
- Рассмотрим два объекта, которые движутся в одном направлении. В этой ситуации величина относительной скорости одного объекта по отношению к другому будет равна разнице в величине их скоростей.
- Если два объекта движутся в одном направлении и с одинаковыми скоростями, их относительная скорость будет ноль.
- Предположим, что любые два объекта движутся в противоположном направлении. В этом случае величина относительной скорости одного объекта по отношению к другому окажется суммой величины их скоростей.
Поучительная задачка на предмет того, насколько мы зашорены и ограничены в мышлении предыдущим опытом решения подобных задач. А также на предмет того, что условие задачи должно должно быть достаточно полным, чтобы позволить однозначно решить задачу.
Давйте попробуем начертить план, на котором обозначим точками города А и В, а также положения автомобиля и мотоцикла в начальный момент времени А0 и М0, а моменты времени 1 час и 2 часа, соответственно точками А1 и А2 и М1 и М2.
Очевидно, что точка А0 совпадает сточкой А (обозначением города), а М0 — с точкой В.
Что нам задано однозначно? «Через час автомобиль был посередине между пунктом А и мотоциклом.».
Т.е. мы можем произвольно поставить точки А0 и М1, соединить их отрезком и на его середине поставить точку А1. Условие «Через час автомобиль был посередине между пунктом А и мотоциклом.» — выполнено. И Всё. Больше нас ничто не ограничивает в наших фантазиях (к условию «Еще через час автомобиль и мотоцикл находились на одинаковом расстоянии от пункта А.» вернёмся чуть позже.
Нигде в условии не сказано, что движение автомобиля и мотоцикла прямолинейное и с постоянными скоростями. Ну ладно, можно согласиться, что вопрос «Найти отношение скоростей мотоцикла и автомобиля» предполагает, что величины скоростей остаются постоянными. Но ведь движение может быть и не по прямой. Начертим на нашем плане ЛЮБУЮ кривую линию Любой длины от точки А0 к точке А1. Затем поставим на плане совершенно ПРОИЗВОЛЬНО точку А2 почти в любом месте с единственным ограничением, чтобы длина прямой А1А2 не превышала длины кривой А0А1 (можно измерить курвиметром. Далее, проведём окружность радиусом А0А2 с центром в точке А0 (т.е. в городе А). Теперь, АБСОЛЮТНО В ЛЮБОМ месте этой окружности поставим точку М2. Теперь условие «Еще через час автомобиль и мотоцикл находились на одинаковом расстоянии от пункта А.» тоже выполнено. От точки М1 до точки М2 мы можем нарисовать любую кривую линию. Далее, от точки М1 мы можем нарисовать любую кривую линию той же длины, что и между М2 и М1, и там поставить точку М0 (город В).
Итак, все условия задачи выполнены, и количество решений у нас — насколько хватает фантазии.
В большинстве школьных задач на движение молчаливо предполагается (если особо не оговаривается, например при беге по кругу на стадионе), что движение происходит по прямой, хотя ЭТО УСЛОВИЕ ОБЯЗАТЕЛНО НУЖНО ОГОВАРИВАТЬ.
Ну ладно, предположим, что у нас в условии сказано, что движение прямолинейное и с постоянной скоростью. Тогда число вариантов значительно уменьшается, но ещё остаётся бесконечно большим.
Начертим план заново. Чертим отрезок А0М1. На середине его ставим точку А1. откладывая от точки А1 отрезок А1А2, равный отрезку А0А1 приходим к точке А2, в этой ситуации она совпадает с точкой М1. Чертим окружность радиуса А0А2 с центром в точке А0. Точку М2 можно поставить в ЛЮБОЙ точке этой окружности. Далее, через точки М2 и М1 провести прямую, и от точки М1 отложить отрезок М1М0, равный по длине отрезку М2М1. И в этом месте поставить точку В.
Итак, даже если бы было оговорено, что движение прямолинейное и всё время в одном направлении, т.е. векторы скоростей не меняются, всё равно получается бесконечное множество решений.
И ТОЛЬКО ЕСЛИ ВВЕСТИ ДОПОЛНИТЕЛЬНОЕ ОГРАНИЧЕНИЕ, ЧТО движение автомобиля и мотоцикла происходит только по прямой, проведённой через точки А и В, то только тогда условие задачи и решение становятся однозначными.
Продолжим радиус А0А2 за точку А0 до пересечения с окружностью. Если точку М2 поставить на этом пересечении, то получится, что за второй час мотоцикл проехал отрезок М1М2, равный диаметру окружности, а автомобиль — отрезок А1А2, равный половине радиуса окружности. Следовательно, скорость мотоцикла в 4 раза выше скорости автомобиля.
А если допустима скорость мотоцикла равная 0, то появляется ещё и второй вариант, когда точки в, А2 М0 М1 и М2 совпадают.
Ну, и напоследок, числовая иллюстрация. Скорость автомобиля 20 км/ч, мотоцикла 80 км/ч. Расстояние между городами равно 120 км. За первый час автомобиль проехал по направлению к городу В 20 км (точка А1). Мотоцикл проехал за это время 80 км по направлению к городу А и находился в 40 км от А (точка М1, она же впоследствии А2). За половину второго часа мотоцикл достиг города А, но не остановился и продолжил движение и к концу второго часа оказался на расстоянии 40 км от города А (точка М2) в противоположную от города В сторону. А автомобиль — в точке А2, она же М1 на линии между городами А и В в 40 км от города А и 80 км от города В.
Под относительностью понимают зависимость чего-либо от выбора системы отсчета. Так, покой и движение тела, его положение в пространстве всегда относительны. Человек, сидящий внутри движущегося автомобиля, покоится относительно этого автомобиля. Но относительно предметов снаружи он движется с некоторой скоростью.
Относительность перемещения
Пусть движение материальной точки (МТ) описывается относительно двух систем отсчета: подвижной (ПСО) и неподвижной (НСО). Зная, как эта точка движется относительно ПСО, и, как ПСО движется относительно НСО, можно вычислить перемещение точки относительно НСО. В этом заключается правило сложения перемещений:
s′ = s1 + s2
s′ — перемещение МТ относительно НСО, s1— перемещение МТ относительно ПСО, s2 — перемещение ПСО относительно НСО.
Чтобы применять правило сложения перемещений, нужно уметь складывать вектора.
Полезные факты
- Если тело движется в направлении движения ПСО, то модуль его перемещения относительно НСО равен сумме модулей перемещения этого тела относительно ПСО и перемещения ПСО относительно НСО:
s′ = s1 + s2
- Если тело движется противоположно движению ПСО, то модуль его перемещения относительно НСО равен разности модулей перемещения этого тела относительно ПСО и перемещения ПСО относительно НСО:
s′ = s1 – s2
- Если тело движется под прямым углом по отношению к направлению движения ПСО, то модуль его перемещения относительно НСО равен корню из суммы квадратов перемещений этого тела относительно ПСО и перемещения ПСО относительно НСО:
s′ = √(s12 + s22)
- Если относительно ПСО тело покоится, то его перемещение относительно НСО равно перемещению ПСО относительно НСО: при s1=0, перемещение s′ = s2
- Если тело движется относительно двух НСО, то его перемещение относительно НСО1 равно перемещению движения относительно НСО2. В этом случае одну из систем можно принять за ПСО с нулевой скоростью. Тогда ее перемещение относительно НСО будет равно 0. При s2=0, перемещение s′ = s1
Пример №1. Человек прошел в автобусе 2 метра в направлении заднего выхода. За это же время автобус успел переместиться относительно остановки на 10 м. Найти перемещение человека относительно автобусной остановки.
Так как человек двигался в сторону конца автобуса, он двигался противоположно его движению. В этом случае его перемещение будет равно модулю разности перемещений, совершенных человеком относительно автобуса и автобусом относительно остановки:
s′=|s1 – s2|=|10 – 2|=8 (м).
Относительность скорости в ПСО и НСО
Тела и системы отсчета могут двигаться с различной скоростью. Но, зная скорость движения МТ относительно ПСО и скорость движения ПСО относительно НСО, можно вычислить скорость движения МТ относительно НСО. В этом заключается правило сложения скоростей:
v′ = v + u
v′ — скорость МТ относительно НСО, v — скорость МТ относительно ПСО, u — скорость движения ПСО относительно НСО.
Складывая векторы скоростей, нужно пользоваться правилами сложения векторов.
Полезные факты
- Если тело движется в направлении движения ПСО, то модуль его скорости относительно НСО равен сумме модулей скорости этого тела относительно ПСО и скорости ПСО относительно НСО:
v′ = v + u
- Если тело движется противоположно движению ПСО, то модуль его скорости относительно НСО равен разности модуля скорости этого тела относительно ПСО и скорости ПСО относительно НСО:
v′ = v – u
- Если тело движется под прямым углом по отношению к направлению движения ПСО, то модуль его скорости относительно НСО равен корню из суммы квадратов скорости этого тела относительно ПСО и скорости ПСО относительно НСО:
v′ = √(v2 + u2)
- Если относительно ПСО тело покоится, то его скорость относительно НСО равна скорости ПСО относительно НСО: при v=0, скорость v′ = u
- Если тело движется относительно двух НСО, то его скорость относительно НСО1 равна скорости движения относительно НСО2. В этом случае одну из неподвижных систем можно принять за ПСО с нулевой скоростью. При u=0, скорость v′ = u
Пример №2. Моторная лодка должна пересечь реку, скорость течения которой равна 5 км/ч, по кратчайшему пути. Собственная скорость лодки равна 10 км/ч. Определить, под каким углом к берегу должна быть направлена лодка, чтобы она не отклонялась от кратчайшего пути.
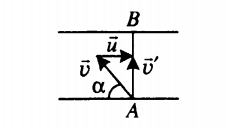
Кратчайшим путем между двумя параллельными линиями является отрезок, заключенный между этими линиями при условии, что он лежит на прямой, пересекающей эти линии под прямым углом. На рисунке этот путь отметим отрезком АВ.
Лодка движется прямолинейно. Поэтому направление ее скорости относительно берега совпадает с направлением перемещения:
Векторы скоростей образуют прямоугольный треугольник, и собственная скорость лодки направлена к берегу под некоторым углом α. Косинус этого угла равен отношению прилегающего катета (скорости лодки относительно реки) к гипотенузе (скорости течения реки):
Косинусу 0,5 соответствует угол, равный 60 градусам.
Относительная скорость двух тел
Понятие относительной скорости вводится, когда рассматривается движение двух тел относительно друг друга внутри одной и той же системы отсчета (СО). Примером служат два движущихся автомобиля, в то время как их движение рассматривается относительно неподвижного объекта.
Относительная скорость равна векторной разности скоростей первого и второго тела относительно СО:
vотн = v1– v2
vотн — относительная скорость, или скорость первого тела относительно второго, v1 и v2 — скорость первого и второго тела относительно СО.
Варианты обозначения относительной скорости и их проекций:
- v12 — скорость первого тела относительно второго. Ее проекция равна:
v12x = v1x – v2x
- v21 — скорость второго тела относительно первого. Ее проекция равна v21x = v2x – v1x
Для вычисления относительной скорости движения тела важно уметь применять правила вычитания векторов.
Полезные факты
- Если тела движутся в одном направлении, то относительная скорость равна модулю разности скоростей первого и второго тела:
vотн = |v1 – v2|
- Если тела движутся в противоположных направлениях, то относительная скорость равна сумме скоростей первого и второго тела:
vотн = |v1 + v2|
- Если тела движутся взаимно перпендикулярно, то относительная скорость равна корню из суммы квадратов скоростей первого и второго тела:
vотн = √(v12 + v22)
Пример №3. Два автомобиля движутся противоположно друг другу. Скорость первого автомобиля относительно дороги равна 100 км/ч. Скорость второго автомобиля относительно первого равна 180 км/ч. Найти модуль скорости второго автомобиля относительно дороги.
Так как автомобили движутся в противоположном направлении, относительная скорость равна сумме скоростей первого и второго автомобиля. Поэтому скорость второго равна разности относительной скорости и скорости движения второго тела, которым в данном случае является первый автомобиль:
Скорость второго автомобиля относительно дороги равна 80 км/час.
Правила сложения векторов
Эта таблица иллюстрирует правила сложения векторов на примере векторов a и b. Результатом их сложения является вектор c .
| Сложение двух сонаправленных векторов | |
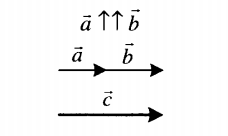 |
Суммой двух сонаправленных векторов является вектор, направленный в ту же сторону.
Его длина равна сумме длин слагаемых векторов: c = a + b. |
| Сложение двух противоположно направленных векторов | |
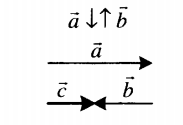 |
Суммой двух противоположно направленных векторов является вектор, направленный в сторону большего по модулю вектора. Его длина равна модулю разности длин слагаемых векторов: c = |a – b|. |
| Сложение двух векторов, расположенных друг к другу под углом | |
| Суммой двух векторов, расположенных друг к другу под углом является вектор, направление которого определяется графически методом треугольника или параллелограмма. Его длина зависит от величины угла, под которым расположены два слагаемых векторов. | |
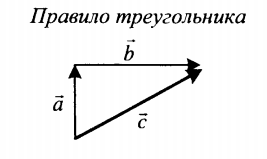 |
Если слагаемые векторы перпендикулярны, для вычисления длины вектора их суммы используется теорема Пифагора:
|
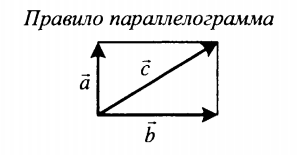 |
|
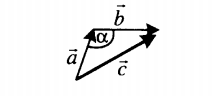 |
Если слагаемые векторы расположены под тупым углом α, для вычисления длины вектора их суммы используется теорема косинусов:
|
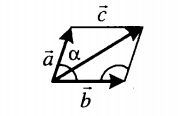 |
Если слагаемые векторы расположены под острым углом α, для вычисления длины вектора их суммы используется теорема косинусов:
|
Правила вычитания векторов
Эта таблица иллюстрирует правила вычитания векторов на примере векторов Результатом их вычитания является вектор
.
| Вычитание двух сонаправленных векторов | |
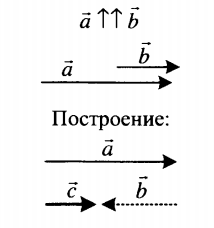 |
Разностью двух сонаправленных векторов является вектор, направленный в сторону большего по модулю вектора.
Его длина равна модулю разности длин вычитаемых векторов: c = |a – b|. |
| Вычитание двух противоположно направленных векторов | |
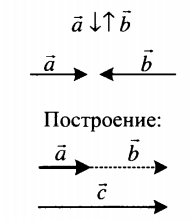 |
Разность двух противоположно направленных векторов есть вектор, направленный в сторону уменьшаемого вектора. Его длина равна сумме длин вычитаемых векторов: c = a + b. |
| Вычитание двух векторов, расположенных друг к другу под углом | |
| Разностью двух векторов, расположенных друг к другу под углом является вектор, являющийся обратным вектору, образующемуся при сложении этих векторов. Его направление определяется графически. Его длина зависит от величины угла, под которым расположены два слагаемых векторов. | |
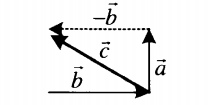 |
Если вычитаемые векторы перпендикулярны, для вычисления длины вектора их разности используется теорема Пифагора:
|
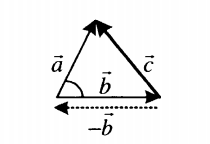 |
Если вычитаемые векторы расположены под углом α, для вычисления длины вектора их разности используется теорема косинусов:
|
Задание EF17727
Два автомобиля движутся по прямому шоссе, первый — со скоростью v, второй — со скоростью –4v. Найти скорость второго автомобиля относительно первого.
Алгоритм решения
- Записать данные в определенной системе отсчета.
- Изобразить графическую модель ситуации задачи.
- Записать классический закон сложения скоростей в векторном виде.
- Записать классический закон сложения скоростей в векторном виде применительно к условиям задачи.
- Найти искомую величину.
Решение
Записываем данные относительно Земли:
- Скорость первого автомобиля относительно оси ОХ: v1 = v.
- Скорость второго автомобиля относительно оси ОХ: v2 = –4v.
Изображаем графическую модель ситуации. Так как у второго автомобиля перед вектором скорости стоит знак «–», первый и второй автомобили движутся во взаимно противоположных направлениях.
Записываем закон сложения скоростей в векторном виде:
v′ = v + u
v′ — скорость второго автомобиля относительно оси ОХ (v2), v — скорость второго автомобиля относительно системы отсчета, связанной с первым автомобилем, u — скорость движения первого автомобиля относительно оси ОХ (v1).
Закон сложения скоростей в векторном виде применительно к условиям задачи будет выглядеть так:
v2 = v + v1
Отсюда:
v = v2 — v1 = –4v – v = –5v
Ответ: -5v
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17518
Два автомобиля движутся в одном направлении. Относительно Земли скорость первого автомобиля 110 км/ч, второго 60 км/ч. Чему равен модуль скорости первого автомобиля в системе отсчёта, связанной со вторым автомобилем?
Алгоритм решения
- Записать данные в определенной системе отсчета.
- Изобразить графическую модель ситуации задачи.
- Записать классический закон сложения скоростей в векторном виде.
- Выбрать систему отсчета.
- Записать классический закон сложения скоростей в скалярном виде.
- Найти искомую величину.
Решение
Записываем данные относительно Земли:
- Скорость первого автомобиля относительно неподвижной системы отсчета: v1 = 110 км/ч;
- Скорость второго автомобиля относительно Земли: v2 = 60 км/ч.
Изображаем графическую модель ситуации:
Записываем закон сложения скоростей в векторном виде:
v′ = v + u
v′ — скорость автомобиля относительно земли (v1), v — скорость второго автомобиля относительно системы отсчета, связанной со вторым автомобилем, u — скорость движения второго автомобиля относительно земли (v2).
По условию задачи в качестве системы отсчета нужно выбрать второй автомобиль. Так как система отсчета, связанная со вторым автомобилем, и первый автомобиль движутся в одном направлении, классический закон сложения скоростей в скалярном виде будет выглядеть так:
v’ = v + u
Отсюда скорость первого автомобиля в системе отсчёта, связанной со вторым автомобилем:
v = v’ – u = v1 – v2 = 110 – 60 = 50 (км/ч).
По условию задачи ответом должен быть модуль этой скорости. Модуль числа 50 есть 50.Ответ: 50
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 7.4k
Чтобы разобраться в относительности механического движения, зададимся вопросом:
«Мы сейчас, в настоящий момент времени, движемся или находимся в состоянии покоя?»
Ты, конечно же, ответишь, что всё зависит от того, что мы делаем.
Просто сидим на месте или двигаемся куда-нибудь.
Однако это не совсем верно.
Дело в том, что даже когда ты сидишь, стоишь или лежишь на одном и том же месте —
ты всё равно движешься!
Как это понять? Да всё очень просто. Я предполагаю, что ты сейчас находишься на планете Земля, так вот знай: она движется вокруг Солнца, таким образом, и ты движешься вместе с Землёй вокруг Солнца.
Магазины и деревья на улице не стоят на месте? Стоя возле них, мы же видим, что они никуда не движутся. Так движутся или нет?
Со всем разобраться поможет слово «относительно».
Пример:
Если ты находишься в движущемся вагоне поезда, то относительно лампочки этого же поезда ты не движешься, а относительно автомобиля, стоящего возле дома, ты движешься.
Рис. (1). Транспорт
Давайте примем дом за неподвижное тело. Правильно оно называется тело отсчёта. Относительно него стоящие рядом деревья находятся на месте, то есть не движутся. А пролетающие рядом птицы и едущие по дороге автомобили находятся в движении.
Чтобы найти скорость движения одного тела относительно другого, необходимо сложить векторы этих скоростей.
Классический закон сложения скоростей гласит:
скорость тела относительно неподвижной системы отсчёта равна геометрической сумме двух скоростей — скорости тела относительно подвижной системы отсчёта и скорости подвижной системы отсчёта относительно неподвижной.
Вспомним, как складываются векторы. Пусть это будут векторы скорости
V→1
и
V→2
.
Вот они направлены в одну сторону, например, так:
Рис. (2). Векторы скорости, расположенные на параллельных прямых
Для того чтобы их сложить, нужно выстроить их друг за другом.
Это называется сложением векторов по правилу треугольника.
Должно получиться так:
Рис. (3). Векторы скорости друг за другом
В результате сложения таких векторов должен получиться один результирующий.
Покажем его красным цветом. Это вектор
V→
.
Он получился, когда мы соединили начало первого вектора с концом последнего.
Рис. (4). Вектор, получившийся в результате сложения
Два вектора
V→1
и
V→2
сложились, и получился один вектор
V→
. Всё просто.
Бывает, что векторы могут быть направлены в разные стороны. Скажем, вот так:
Рис. (5). Векторы направлены в разные стороны, расположены на параллельных прямых
Будем пробовать их складывать по известному правилу — правилу треугольника.
Выстроим векторы друг за другом. Должно получиться примерно так:
Рис. (6). Выстроенные вместе векторы
Снова соединим начало первого вектора с концом последнего.
Чтобы было лучше видно, изобразим результирующий вектор красным цветом.
Рис. (7). Результирующий вектор
Два вектора
V→1
и
V→2
сложились, и получился один вектор
V→
.
Может случиться, что векторы лежат не так ровно, а, скажем, под углом (90°) друг к другу.
Например:
Рис. (8). Векторы, перпендикулярные друг другу
Перед нами два вектора —
V→1
и
V→2
. Как же их сложить?
Снова выстраиваем их друг за другом, чтобы получились стороны треугольника.
Или соединяем начала этих векторов — тогда получится правило параллелограмма.
Рис. (9). Соединённые векторы
Правило треугольника нам уже знакомо. Просто соединяем начало первого вектора с концом последнего.
Для сложения по правилу параллелограмма дорисовываем ещё две стороны напротив уже имеющихся двух.
Результат сложения не зависит от выбранного правила сложения — правила треугольника или правила параллелограмма.
Должен получиться один и тот же вектор
V→
. Изобразим его красным.
Рис. (10). Результирующий вектор по правилу параллелограмма
Теперь можно приступать к решению задач на относительное движение.
Источники:
Рис. (2). Векторы скорости, расположенные на параллельных прямых. © ЯКласс.
Рис. (3). Векторы скорости друг за другом. © ЯКласс.
Рис. (4). Вектор, получившийся в результате сложения. © ЯКласс.
Рис. (5). Векторы направлены в разные стороны, расположены на параллельных прямых. © ЯКласс.
Рис. (6). Выстроенные вместе векторы. © ЯКласс.
Рис. (7). Результирующий вектор. © ЯКласс.
Рис. (8). Векторы, перпендикулярные друг другу. © ЯКласс.
Рис. (9). Соединённые векторы. © ЯКласс.
Рис. (10). Результирующий вектор по правилу параллелограмма. © ЯКласс.
Основные понятия кинематики
Кинематика – раздел физики, в котором даётся описание механического движения без выяснения причин, которые приводят к этому движению.
Механическое движение – это изменение взаимного расположения тел или частей тела.
Механическое движение можно наблюдать только относительно других тел. В различных системах отсчёта физические величины, характеризующие движение, и характер движения могут быть различными. Например, автомобиль движется по дороге. В автомобиле находятся люди. Люди движутся вместе с автомобилем по дороге. То есть люди перемещаются в пространстве относительно дороги. Но относительно самого автомобиля люди не движутся.
Система отсчёта, относительно которой описывается движение, состоит из:
- тела отсчёта – условно неподвижное тело;
- системы координат и часов, связанной с телом отсчёта.
При движении тело описывает некоторую линию, которая называется траекторией движения.
Траектория движения – это множество точек, которые определяют положение тела в тот или иной момент времени.
Основные виды механического движения:
- поступательное – это движение тела, при котором прямая, соединяющая две любые точки тела, переносится всё время параллельно первоначальному положению (кузов автомобиля совершает поступательное движение при движении автомобиля по дороге);
- вращательное – это движение тела вокруг некоторой оси. При таком движении все точки тела совершают движение по окружностям, центром которых является эта ось (колёса совершают вращательное движение при движении автомобиля по дороге);
- колебательное – движение, при котором тело проходит положение равновесия, каждый раз двигаясь в направлении, противоположном предыдущему (колебательное движение совершает маятник в часах).
Скорость является основной характеристикой механического движения. Скорость – это быстрота перемещения.
Перемещение – векторная величина, связывающая две любые точки траектории.
, где
– скорость;
– перемещение;
– время, затраченное на перемещение.
Скорость – это векторная величина, всегда направленная по касательной к траектории движения в каждой её точке.
Средняя скорость – отношение всего пройденного пути к затраченному на это движение времени.
,
где – средняя скорость;
– весь пройденный путь;
– всё затраченное время.
Понятием относительной скорости пользуются в том случае, когда рассматривают движение одного тела по отношению к другому телу. Например, движутся два автомобиля навстречу друг другу, их относительная скорость будет равна сумме скоростей (см. рис. 1). Если бы эти автомобили двигались в одном направлении, то относительная скорость была бы равна скорости второго минус скорость первого (см. рис. 1).
Рис. 1. Относительная скорость
В любом случае, относительная скорость равна векторной разности скоростей:
Сложение перемещений и скоростей проводится по правилу сложения векторов. Векторы складываются по правилу треугольника или по правилу параллелограмма (см. рис. 2).
Рис. 2. Правила сложения векторов
Задача 1
Половину пути пешеход прошёл со скоростью . А вторую – со скоростью
. Чему равна средняя скорость пешехода?
Дано: ;
– путь, пройденный на первом участке;
;
– путь, пройденный на втором участке
Найти:
Решение
Общее время состоит из двух отрезков времени:
Время первой половины пути:
Время второй половины пути:
Подставляем данное выражение в формулу средней скорости:
Ответ: .
Задача 2
Лодка, развивающая относительно воды скорость 5 м/с, пересекает реку шириной 40 м по наикратчайшему пути. Найти время переправы, если скорость течения реки – 3 м/с.
Дано: ;
;
Найти:
Решение
Для того чтобы пересечь реку, то есть пройти из пункта А в пункт В, необходимо направить лодку против течения реки под определённым углом (см. рис. 3). При этом к скорости лодки добавится скорость течения реки
и результирующая скорость
будет направлена по прямой АВ. Это можно записать в виде следующего векторного соотношения:
Рис. 3. Иллюстрация к задаче
Так как , то треугольник скоростей является прямоугольным. Если посмотреть на цифровые значения сторон этого треугольника (см. рис. 4), то окажется, что это египетский треугольник. Если гипотенуза равна 5, а один из катетов – 3, то второй катет равен 4.
Рис. 4. Египетский треугольник
Следовательно, скорость, с которой лодка пересекает речку, равна 4:
Время переправы находится по формуле:
Ответ: .
Задача 3
Найти относительную скорость двух автомобилей, движущихся по двум дорогам, пересекающимся под , в одном направлении со скоростями по 30 м/с. Варианты ответов: 1. 0 м/с; 2. 30 м/с; 3. 60 м/с; 4. 45 м/с.
Дано: ;
Найти:
Решение
Относительная скорость второго автомобиля по отношению к первому равна:
На рисунке 5 выполнен схематический рисунок к задаче.
Рис. 5. Иллюстрация к задаче
Для того чтобы найти разность двух векторов, необходимо выражение относительной скорости представить в таком виде:
Тогда к концу вектора прикладывается начало вектора
и эти вектора соединяются. Полученный вектор является вектором относительной скорости.
Треугольник скоростей является равнобедренным, с углом при вершине , следовательно:
Ответ: 2. 30 м/с.
Список литературы
- Г. Я. Мякишев, Б. Б. Буховцев, Н. Н. Сотский. Физика 10. – М.: Просвещение, 2008.
- А. П. Рымкевич. Физика. Задачник 10–11. – М.: Дрофа, 2006.
- О. Я. Савченко. Задачи по физике. – М.: Наука, 1988.
- А. В. Пёрышкин, В. В. Крауклис. Курс физики. Т. 1. – М.: Гос. уч.-пед. изд. мин. просвещения РСФСР, 1957.
- Орлов В. А., Демидова М. Ю., Никифоров Г. Г., Ханнанов Н. К. Оптимальный банк заданий для подготовки к ЕГЭ. Единый государственный экзамен 2015. Физика. Учебное пособие. – М.: Интеллект-Центр, 2015.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Интернет-портал «physics.ru» (Источник)
- Интернет-портал «indigomath.ru» (Источник)
- Интернет-портал «afportal.ru» (Источник)
Домашнее задание
- Упражнение 2 (1, 2) стр. 27 – Г. Я. Мякишев, Б. Б. Буховцев, Н. Н. Сотский. Физика 10 (см. список рекомендованной литературы)
- Какие виды механического движения вам известны?
- Самолет летит с грузом к месту назначения на высоте 405 м над песчаной местностью с горизонтальным профилем со скоростью 130 м/с. Чтобы груз попал в намеченное место на земле (силой сопротивления движения пренебречь), летчик должен освободить его от крепежа, не долетев до цели. Варианты ответа: 1. 0,53 км 3. 0,95 км 2. 0,81 км 4. 1,17 км
- Поезд половину пути проехал со скоростью 72 км/ч, а вторую половину – в 1,5 раза медленнее. Определить среднюю скорость на всем пути.