From Wikipedia, the free encyclopedia
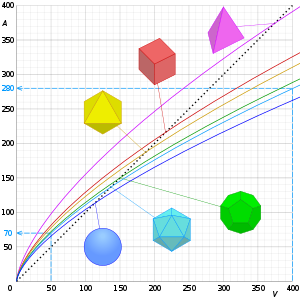
Graphs of surface area, A against volume, V of the Platonic solids and a sphere, showing that the surface area decreases for rounder shapes, and the surface-area-to-volume ratio decreases with increasing volume. Their intercepts with the dashed lines show that when the volume increases 8 (2³) times, the surface area increases 4 (2²) times.
The surface-area-to-volume ratio (surface-to-volume ratio, denoted as sa/vol, SA/V or SA:V, is the amount of surface area per unit volume of an object or collection of objects.
SA:V is an important concept in science and engineering. It is used to explain the relation between structure and function in processes occurring through the surface and the volume. Good examples for such processes are processes governed by the heat equation,[1] that is, diffusion and heat transfer by thermal conduction.[2] SA:V is used to explain the diffusion of small molecules, like oxygen and carbon dioxide between air, blood and cells,[3] water loss by animals,[4] bacterial morphogenesis,[5] organism’s thermoregulation,[6] design of artificial bone tissue,[7] artificial lungs [8] and many more biological and biotechnological structures. For more examples see Glazier.[9]
The relation between SA:V and diffusion or heat conduction rate is explained from flux and surface perspective, focusing on the surface of a body as the place where diffusion, or heat conduction, takes place, i.e., the larger the SA:V there is more surface area per unit volume through which material can diffuse, therefore, the diffusion or heat conduction, will be faster. Similar explanation appears in the literature: «Small size implies a large ratio of surface area to volume, thereby helping to maximize the uptake of nutrients across the plasma membrane»,[10] and elsewhere.[9][11][12]
For a given volume, the object with the smallest surface area (and therefore with the smallest SA:V) is a ball, a consequence of the isoperimetric inequality in 3 dimensions. By contrast, objects with acute-angled spikes will have very large surface area for a given volume.
SA:V for balls and n-balls[edit]
A ball is a three-dimensional object, being the solid version of a sphere. (In geometry, the term sphere properly refers only to the surface, so a sphere thus lacks volume in this context.) Balls exist in any dimension and are generically called n-balls, where n is the number of dimensions.
Plot of the surface-area:volume ratio (SA:V) for a 3-dimensional ball, showing the ratio decline inversely as the radius of the ball increases.
For an ordinary three-dimensional ball, the SA:V can be calculated using the standard equations for the surface and volume, which are, respectively, 

The same reasoning can be generalized to n-balls using the general equations for volume and surface area, which are:
volume = 

Plot of surface-area:volume ratio (SA:V) for n-balls as a function of the number of dimensions and of radius size. Note the linear scaling as a function of dimensionality and the inverse scaling as a function of radius.
So the ratio reduces to 
Dimension[edit]
The surface-area-to-volume ratio has physical dimension L−1 (inverse length) and is therefore expressed in units of inverse distance. As an example, a cube with sides of length 1 cm will have a surface area of 6 cm2 and a volume of 1 cm3. The surface to volume ratio for this cube is thus
.
For a given shape, SA:V is inversely proportional to size. A cube 2 cm on a side has a ratio of 3 cm−1, half that of a cube 1 cm on a side. Conversely, preserving SA:V as size increases requires changing to a less compact shape.
Physical chemistry[edit]
Materials with high surface area to volume ratio (e.g. very small diameter, very porous, or otherwise not compact) react at much faster rates than monolithic materials, because more surface is available to react. An example is grain dust: while grain is not typically flammable, grain dust is explosive. Finely ground salt dissolves much more quickly than coarse salt.
A high surface area to volume ratio provides a strong «driving force» to speed up thermodynamic processes that minimize free energy.
Biology[edit]
The ratio between the surface area and volume of cells and organisms has an enormous impact on their biology, including their physiology and behavior. For example, many aquatic microorganisms have increased surface area to increase their drag in the water. This reduces their rate of sink and allows them to remain near the surface with less energy expenditure.[citation needed]
An increased surface area to volume ratio also means increased exposure to the environment. The finely-branched appendages of filter feeders such as krill provide a large surface area to sift the water for food.[13]
Individual organs like the lung have numerous internal branchings that increase the surface area; in the case of the lung, the large surface supports gas exchange, bringing oxygen into the blood and releasing carbon dioxide from the blood.[14][15] Similarly, the small intestine has a finely wrinkled internal surface, allowing the body to absorb nutrients efficiently.[16]
Cells can achieve a high surface area to volume ratio with an elaborately convoluted surface, like the microvilli lining the small intestine.[17]
Increased surface area can also lead to biological problems. More contact with the environment through the surface of a cell or an organ (relative to its volume) increases loss of water and dissolved substances. High surface area to volume ratios also present problems of temperature control in unfavorable environments.[citation needed]
The surface to volume ratios of organisms of different sizes also leads to some biological rules such as Allen’s rule, Bergmann’s rule[18][19][20] and gigantothermy.[21]
Fire spread[edit]
In the context of wildfires, the ratio of the surface area of a solid fuel to its volume is an important measurement. Fire spread behavior is frequently correlated to the surface-area-to-volume ratio of the fuel (e.g. leaves and branches). The higher its value, the faster a particle responds to changes in environmental conditions, such as temperature or moisture. Higher values are also correlated to shorter fuel ignition times, and hence faster fire spread rates.
Planetary cooling[edit]
A body of icy or rocky material in outer space may, if it can build and retain sufficient heat, develop a differentiated interior and alter its surface through volcanic or tectonic activity. The length of time through which a planetary body can maintain surface-altering activity depends on how well it retains heat, and this is governed by its surface area-to-volume ratio. For Vesta (r=263 km), the ratio is so high that astronomers were surprised to find that it did differentiate and have brief volcanic activity. The moon, Mercury and Mars have radii in the low thousands of kilometers; all three retained heat well enough to be thoroughly differentiated although after a billion years or so they became too cool to show anything more than very localized and infrequent volcanic activity. As of April 2019, however, NASA has announced the detection of a «marsquake» measured on April 6, 2019, by NASA’s InSight lander.[22] Venus and Earth (r>6,000 km) have sufficiently low surface area-to-volume ratios (roughly half that of Mars and much lower than all other known rocky bodies) so that their heat loss is minimal.[23]
Mathematical examples[edit]
| Shape | Characteristic length 
|
Surface area | Volume | SA/V ratio | SA/V ratio for unit volume |
|
|---|---|---|---|---|---|---|
| Tetrahedron | 
|
edge | 
|

|

|
7.21 |
| Cube | 
|
edge | 
|

|

|
6 |
| Octahedron | 
|
edge | 
|

|

|
5.72 |
| Dodecahedron | 
|
edge | 
|

|

|
5.31 |
| Capsule | 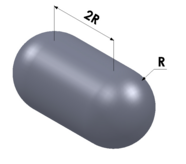
|
radius (R) | 
|

|

|
5.251 |
| Icosahedron | 
|
edge | 
|

|

|
5.148 |
| Sphere | 
|
radius | 
|

|

|
4.83598 |
| Side of cube |
Side2 | Area of a single face |
6 × side2 | Area of entire cube (6 faces) |
Side3 | Volume | Ratio of surface area to volume |
|---|---|---|---|---|---|---|---|
| 2 | 2×2 | 4 | 6×2×2 | 24 | 2×2×2 | 8 | 3:1 |
| 4 | 4×4 | 16 | 6×4×4 | 96 | 4×4×4 | 64 | 3:2 |
| 6 | 6×6 | 36 | 6×6×6 | 216 | 6×6×6 | 216 | 3:3 |
| 8 | 8×8 | 64 | 6×8×8 | 384 | 8×8×8 | 512 | 3:4 |
| 12 | 12×12 | 144 | 6×12×12 | 864 | 12×12×12 | 1,728 | 3:6 |
| 20 | 20×20 | 400 | 6×20×20 | 2,400 | 20×20×20 | 8,000 | 3:10 |
| 50 | 50×50 | 2,500 | 6×50×50 | 15,000 | 50×50×50 | 125,000 | 3:25 |
| 1,000 | 1,000×1,000 | 1,000,000 | 6×1,000×1,000 | 6,000,000 | 1,000×1,000×1,000 | 1,000,000,000 | 3:500 |
See also[edit]
- Compactness measure of a shape
- Dust explosion
- Square–cube law
- Specific surface area
References[edit]
- Schmidt-Nielsen, Knut (1984). Scaling: Why is Animal Size so Important?. New York, NY: Cambridge University Press. ISBN 978-0-521-26657-4. OCLC 10697247.
- Vogel, Steven (1988). Life’s Devices: The Physical World of Animals and Plants. Princeton, NJ: Princeton University Press. ISBN 978-0-691-08504-3. OCLC 18070616.
- Specific
- ^ Planinšič, Gorazd; Vollmer, Michael (February 20, 2008). «The surface-to-volume ratio in thermal physics: from cheese cube physics to animal metabolism». European Journal of Physics. 29 (2): 369–384. Bibcode:2008EJPh…29..369P. doi:10.1088/0143-0807/29/2/017. S2CID 55488270. Retrieved 9 July 2021.
- ^ Planinšič, Gorazd (2008). «The surface-to-volume ratio in thermal physics: from cheese cube physics to animal metabolism». European Journal of Physics European Physical Society, Find Out More. 29 (2): 369–384. Bibcode:2008EJPh…29..369P. doi:10.1088/0143-0807/29/2/017. S2CID 55488270.
- ^ Williams, Peter; Warwick, Roger; Dyson, Mary; Bannister, Lawrence H. (2005). Gray’s Anatomy (39 ed.). Churchill Livingstone. pp. 1278–1282.
- ^ Jeremy M., Howard; Hannah-Beth, Griffis; Westendorf, Rachel; Williams, Jason B. (2019). «The influence of size and abiotic factors on cutaneous water loss». Advances in Physiology Education. 44 (3): 387–393. doi:10.1152/advan.00152.2019. PMID 32628526.
- ^ Harris, Leigh K.; Theriot, Julie A. (2018). «Surface Area to Volume Ratio: A Natural Variable for Bacterial Morphogenesis». Trends in Microbiology. 26 (10): 815–832. doi:10.1016/j.tim.2018.04.008. PMC 6150810. PMID 29843923.
- ^ Louw, Gideon N. (1993). Physiological Animal Ecology. Longman Pub Group.
- ^ Nguyen, Thanh Danh; Olufemi E., Kadri; Vassilios I., Sikavitsas; Voronov, Roman S. (2019). «Scaffolds with a High Surface Area-to-Volume Ratio and Cultured Under Fast Flow Perfusion Result in Optimal O2 Delivery to the Cells in Artificial Bone Tissues». Applied Sciences. 9 (11): 2381. doi:10.3390/app9112381.
- ^ J. K, Lee; H. H., Kung; L. F., Mockros (2008). «Microchannel Technologies for Artificial Lungs: (1) Theory». ASAIO Journal. 54 (4): 372–382. doi:10.1097/MAT.0b013e31817ed9e1. PMID 18645354. S2CID 19505655.
- ^ a b Glazier, Douglas S. (2010). «A unifying explanation for diverse metabolic scaling in animals and plants». Biological Reviews. 85 (1): 111–138. doi:10.1111/j.1469-185X.2009.00095.x. PMID 19895606. S2CID 28572410.
- ^ Alberts, Bruce (2002). «The Diversity of Genomes and the Tree of Life». Molecular Biology of the Cell, 4th edition. New York: Garland Science. ISBN 0-8153-3218-1. ISBN 0-8153-4072-9.
- ^ Adam, John (2020-01-01). «What’s Your Sphericity Index? Rationalizing Surface Area and Volume». Virginia Mathematics Teacher. 46 (2).
- ^ Okie, Jordan G. (March 2013). «General models for the spectra of surface area scaling strategies of cells and organisms: fractality, geometric dissimilitude, and internalization». The American Naturalist. 181 (3): 421–439. doi:10.1086/669150. ISSN 1537-5323. PMID 23448890. S2CID 23434720.
- ^ Kils, U.: Swimming and feeding of Antarctic Krill, Euphausia superba — some outstanding energetics and dynamics — some unique morphological details. In Berichte zur Polarforschung, Alfred Wegener Institute for Polar and Marine Research, Special Issue 4 (1983): «On the biology of Krill Euphausia superba«, Proceedings of the Seminar and Report of Krill Ecology Group, Editor S. B. Schnack, 130-155 and title page image.
- ^ Tortora, Gerard J.; Anagnostakos, Nicholas P. (1987). Principles of anatomy and physiology (Fifth ed.). New York: Harper & Row, Publishers. pp. 556–582. ISBN 978-0-06-350729-6.
- ^ Williams, Peter L; Warwick, Roger; Dyson, Mary; Bannister, Lawrence H. (1989). Gray’s Anatomy (Thirty-seventh ed.). Edinburgh: Churchill Livingstone. pp. 1278–1282. ISBN 0443-041776.
- ^ Romer, Alfred Sherwood; Parsons, Thomas S. (1977). The Vertebrate Body. Philadelphia, PA: Holt-Saunders International. pp. 349–353. ISBN 978-0-03-910284-5.
- ^ Krause J. William (July 2005). Krause’s Essential Human Histology for Medical Students. Universal-Publishers. pp. 37–. ISBN 978-1-58112-468-2. Retrieved 25 November 2010.
- ^ Meiri, S.; Dayan, T. (2003-03-20). «On the validity of Bergmann’s rule». Journal of Biogeography. 30 (3): 331–351. doi:10.1046/j.1365-2699.2003.00837.x. S2CID 11954818.
- ^ Ashton, Kyle G.; Tracy, Mark C.; Queiroz, Alan de (October 2000). «Is Bergmann’s Rule Valid for Mammals?». The American Naturalist. 156 (4): 390–415. doi:10.1086/303400. JSTOR 10.1086/303400. PMID 29592141. S2CID 205983729.
- ^ Millien, Virginie; Lyons, S. Kathleen; Olson, Link; et al. (May 23, 2006). «Ecotypic variation in the context of global climate change: Revisiting the rules». Ecology Letters. 9 (7): 853–869. doi:10.1111/j.1461-0248.2006.00928.x. PMID 16796576.
- ^ Fitzpatrick, Katie (2005). «Gigantothermy». Davidson College. Archived from the original on 2012-06-30. Retrieved 2011-12-21.
- ^ «Marsquake! NASA’s InSight Lander Feels Its 1st Red Planet Tremor». Space.com. 23 April 2019.
- ^ «Archived copy» (PDF). Archived from the original (PDF) on 2018-06-13. Retrieved 2018-08-22.
{{cite web}}: CS1 maint: archived copy as title (link)
External links[edit]
- Sizes of Organisms: The Surface Area:Volume Ratio Archived 2017-08-14 at the Wayback Machine
- National Wildfire Coordinating Group: Surface Area to Volume Ratio
- Previous link not working, references are in this document, PDF
Further reading[edit]
- On Being the Right Size, J.B.S. Haldane Archived 2011-08-22 at the Wayback Machine
Отношение площади поверхности к объему, также называемое отношением площади поверхности к объему и по-разному обозначаемое sa / vol или SA: V, представляет собой величину площади поверхности на единицу объема объекта или совокупности объектов.
SA: V — важное понятие в науке и технике. Он используется для объяснения взаимосвязи между структурой и функцией в процессах, происходящих через поверхность И объем. Хорошими примерами таких процессов являются процессы, регулируемые уравнением теплопроводности, т. Е. Диффузия и теплопередача за счет теплопроводности. SA: V используется для объяснения диффузии малых молекул, таких как кислород и углекислый газ, между воздухом, кровью и клетками, потери воды животными, бактериального морфогенеза, терморегуляции организма, создания искусственной костной ткани, искусственных легких и многих других биологических и биотехнологических конструкции. Для получения дополнительных примеров см. Стекольщик.
Связь между SA: V и скоростью диффузии или теплопроводности объясняется с точки зрения потока и поверхности, фокусируясь на поверхности тела как на месте, где происходит диффузия или теплопроводность, т. Е. Чем больше SA: V большая площадь поверхности на единицу объема, через которую материал может диффундировать, следовательно, диффузия или теплопроводность будут быстрее. Аналогичное объяснение встречается в литературе: «Маленький размер подразумевает большое отношение площади поверхности к объему, тем самым помогая максимизировать поглощение питательных веществ через плазматическую мембрану» и в других местах.
Для данного объема объект с наименьшей площадью поверхности (и, следовательно, с наименьшим SA: V) является шаром, что является следствием изопериметрического неравенства в трех измерениях. Напротив, объекты с остроугольными шипами будут иметь очень большую площадь поверхности для данного объема.
СОДЕРЖАНИЕ
- 1 SA: V для шаров и N-шаров
- 2 измерение
- 3 Физическая химия
- 4 Биология
- 5 Распространение огня
- 6 Планетарное охлаждение
- 7 математических примеров
- 8 См. Также
- 9 ссылки
- 10 Внешние ссылки
- 11 Дальнейшее чтение
SA: V для мячей и N-мячей
Шар представляет собой трехмерный объект, будучи заполненные версии сферы ( «сфера» должным образом относится только к поверхности и, следовательно, сфера не имеет объема). Шары существуют в любом измерении и обычно называются n-шарами, где n — количество измерений.
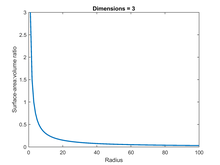
Для обычного трехмерного шара SA: V можно рассчитать, используя стандартные уравнения для поверхности и объема, которые соответственно равны и. Для единичного случая, когда r = 1, SA: V, таким образом, равен 3. SA: V имеет обратную связь с радиусом — если радиус удваивается, SA: V делится пополам (см. Рисунок). 4 π р 2 { Displaystyle 4 pi {г ^ {2}}}
Те же рассуждения можно обобщить на n-шары, используя общие уравнения для объема и площади поверхности, а именно:
объем = ; площадь поверхности = р п π п / 2 Γ ( 1 + п / 2 ) { Displaystyle г ^ {п} пи ^ {п / 2} над Гамма (1 + п / 2)}

Таким образом, соотношение уменьшается до. Таким образом, такая же линейная зависимость между площадью и объемом сохраняется для любого количества измерений (см. Рисунок): удвоение радиуса всегда уменьшает соотношение вдвое. п р — 1 { displaystyle nr ^ {- 1}}
Измерение
Отношение площади поверхности к объему имеет физический размер L -1 (обратная длина) и поэтому выражается в единицах обратного расстояния. Например, куб со сторонами длиной 1 см будет иметь площадь поверхности 6 см 2 и объем 1 см 3. Таким образом, отношение поверхности к объему для этого куба равно
- SA: V знак равно 6 см 2 1 см 3 знак равно 6 см — 1 { displaystyle { t_dv {SA: V}} = { frac {6 ~ { t_dv {cm}} ^ {2}} {1 ~ { t_dv {cm}} ^ {3}}} = 6 ~ { t_dv {см}} ^ {- 1}}
.
Для данной формы SA: V обратно пропорционален размеру. Куб со стороной 2 см имеет отношение 3 см -1, что вдвое меньше, чем у куба со стороной 1 см. И наоборот, сохранение SA: V по мере увеличения размера требует перехода к менее компактной форме.
Физическая химия
Смотрите также: Взрыв пыли
Материалы с высоким отношением площади поверхности к объему (например, очень маленького диаметра, очень пористые или некомпактные ) реагируют гораздо быстрее, чем монолитные материалы, потому что для реакции доступна большая поверхность. Примером может служить зерновая пыль: хотя зерно обычно не воспламеняется, зерновая пыль взрывоопасна. Соль мелкого помола растворяется намного быстрее, чем соль крупного помола.
Высокое отношение площади поверхности к объему обеспечивает сильную «движущую силу» для ускорения термодинамических процессов, которые сводят к минимуму свободную энергию.
Биология
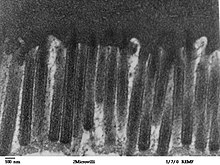
Соотношение между площадью поверхности и объемом клеток и организмов оказывает огромное влияние на их биологию, включая их физиологию и поведение. Например, многие водные микроорганизмы имеют увеличенную площадь поверхности, чтобы увеличить сопротивление воды. Это снижает скорость их погружения и позволяет им оставаться у поверхности с меньшими затратами энергии.
Увеличение отношения площади поверхности к объему также означает повышенное воздействие окружающей среды. Мелкоразветвленные отростки фильтров-питателей, таких как криль, обеспечивают большую площадь поверхности для просеивания воды в поисках пищи.
Отдельные органы, такие как легкое, имеют многочисленные внутренние разветвления, увеличивающие площадь поверхности; в случае легких большая поверхность поддерживает газообмен, доставляя кислород в кровь и высвобождая углекислый газ из крови. Точно так же тонкий кишечник имеет мелко морщинистую внутреннюю поверхность, позволяющую организму эффективно усваивать питательные вещества.
Клетки могут достигать высокого отношения площади поверхности к объему с тщательно извилистой поверхностью, как у микроворсинок, выстилающих тонкий кишечник.
Увеличенная площадь поверхности также может привести к биологическим проблемам. Более тесный контакт с окружающей средой через поверхность клетки или органа (относительно его объема) увеличивает потерю воды и растворенных веществ. Высокое отношение площади поверхности к объему также создает проблемы с контролем температуры в неблагоприятных условиях окружающей среды.
Поверхности к объему организмов различных размеров, также приводит к некоторым биологическим правилам, таким, как правило Аллена, правило Бергмана и gigantothermy.
Распространение огня
В контексте лесных пожаров важным измерением является отношение площади поверхности твердого топлива к его объему. Поведение при распространении огня часто коррелирует с отношением площади поверхности к объему топлива (например, листьев и ветвей). Чем выше его значение, тем быстрее частица реагирует на изменения условий окружающей среды, таких как температура или влажность. Более высокие значения также коррелируют с более коротким временем воспламенения топлива и, следовательно, более высокой скоростью распространения пожара.
Планетарное охлаждение
Тело из ледяного или каменистого материала в космическом пространстве может, если оно может накапливать и сохранять достаточное количество тепла, образовывать дифференцированный интерьер и изменять свою поверхность в результате вулканической или тектонической активности. Продолжительность времени, в течение которого планетарное тело может поддерживать активность по изменению поверхности, зависит от того, насколько хорошо оно сохраняет тепло, и это регулируется соотношением площади поверхности к объему. Для Весты (r = 263 км) это отношение настолько велико, что астрономы были удивлены, обнаружив, что она действительно дифференцировалась и имела кратковременную вулканическую активность. Луна, Меркурий и Марс имеют радиусы в низких тысячах километров; все три достаточно хорошо сохраняли тепло, чтобы их можно было тщательно дифференцировать, хотя примерно через миллиард лет они стали слишком холодными, чтобы показывать что-либо, кроме очень ограниченной и редкой вулканической активности. Однако по состоянию на апрель 2019 года НАСА объявило об обнаружении «маротрясения», измеренного 6 апреля 2019 года спускаемым аппаратом НАСА InSight. Венера и Земля (rgt; 6000 км) имеют достаточно низкие отношения площади поверхности к объему (примерно вдвое меньше, чем у Марса и намного ниже, чем у всех других известных скалистых тел), так что их тепловые потери минимальны.
Математические примеры
| Форма | Характерная длина а { displaystyle a} |
Площадь поверхности | Объем | Соотношение SA / V | Соотношение SA / V для единицы объема | |
|---|---|---|---|---|---|---|
| Тетраэдр |  |
край | 3 а 2 { displaystyle { sqrt {3}} а ^ {2}} |
2 а 3 12 { displaystyle { frac {{ sqrt {2}} а ^ {3}} {12}}} |
6 6 а ≈ 14,697 а { displaystyle { frac {6 { sqrt {6}}} {a}} приблизительно { frac {14.697} {a}}} |
7.21 |
| Куб |  |
боковая сторона | 6 а 2 { displaystyle 6a ^ {2}} |
а 3 { displaystyle a ^ {3}} |
6 а { displaystyle { frac {6} {a}}} |
6 |
| Октаэдр |  |
боковая сторона | 2 3 а 2 { displaystyle 2 { sqrt {3}} а ^ {2}} |
1 3 2 а 3 { displaystyle { frac {1} {3}} { sqrt {2}} а ^ {3}} |
3 6 а ≈ 7,348 а { displaystyle { frac {3 { sqrt {6}}} {a}} приблизительно { frac {7.348} {a}}} |
5,72 |
| Додекаэдр |  |
боковая сторона | 3 25 + 10 5 а 2 { displaystyle 3 { sqrt {25 + 10 { sqrt {5}}}} а ^ {2}} |
1 4 ( 15 + 7 5 ) а 3 { displaystyle { frac {1} {4}} (15 + 7 { sqrt {5}}) а ^ {3}} |
12 25 + 10 5 ( 15 + 7 5 ) а ≈ 2,694 а { displaystyle { frac {12 { sqrt {25 + 10 { sqrt {5}}}}} {(15 + 7 { sqrt {5}}) a}} приблизительно { frac {2.694} { а}}} |
5,31 |
| Капсула |  |
радиус (R) | 4 π а 2 + 2 π а ⋅ 2 а знак равно 8 π а 2 { displaystyle 4 pi a ^ {2} +2 pi a cdot 2a = 8 pi a ^ {2}} |
4 π а 3 3 + π а 2 ⋅ 2 а знак равно 10 π а 3 3 { displaystyle { frac {4 pi a ^ {3}} {3}} + pi a ^ {2} cdot 2a = { frac {10 pi a ^ {3}} {3}}} |
12 5 а { displaystyle { frac {12} {5a}}} |
5,251 |
| Икосаэдр |  |
боковая сторона | 5 3 а 2 { displaystyle 5 { sqrt {3}} а ^ {2}} |
5 12 ( 3 + 5 ) а 3 { displaystyle { frac {5} {12}} (3 + { sqrt {5}}) а ^ {3}} |
12 3 ( 3 + 5 ) а ≈ 3,970 а { displaystyle { frac {12 { sqrt {3}}} {(3 + { sqrt {5}}) a}} приблизительно { frac {3.970} {a}}} |
5,148 |
| Сфера |  |
радиус | 4 π а 2 { displaystyle 4 pi a ^ {2}} |
4 π а 3 3 { displaystyle { frac {4 pi a ^ {3}} {3}}} |
3 а { displaystyle { frac {3} {а}}} |
4,83598 |
| Сторона куба | Сторона 2 | Площадь одного лица | 6 × сторона 2 | Площадь всего куба (6 граней) | Сторона 3 | Объем | Отношение площади поверхности к объему |
|---|---|---|---|---|---|---|---|
| 2 | 2×2 | 4 | 6x2x2 | 24 | 2x2x2 | 8 | 3: 1 |
| 4 | 4×4 | 16 | 6x4x4 | 96 | 4x4x4 | 64 | 3: 2 |
| 6 | 6×6 | 36 | 6x6x6 | 216 | 6x6x6 | 216 | 3: 3 |
| 8 | 8×8 | 64 | 6x8x8 | 384 | 8x8x8 | 512 | 3: 4 |
| 12 | 12×12 | 144 | 6x12x12 | 864 | 12x12x12 | 1728 | 3: 6 |
| 20 | 20×20 | 400 | 6x20x20 | 2400 | 20x20x20 | 8000 | 3:10 |
| 50 | 50×50 | 2500 | 6x50x50 | 15000 | 50x50x50 | 125000 | 3:25 |
| 1000 | 1000×1000 | 1000000 | 6x1000x1000 | 6000000 | 1000x1000x1000 | 1000000000 | 3: 500 |
Смотрите также
- Мера компактности формы
- Взрыв пыли
- Закон квадрата-куба
- Удельная поверхность
использованная литература
- Шмидт-Нильсен, Кнут (1984). Масштабирование: почему так важен размер животного?. Нью-Йорк, Нью-Йорк: Издательство Кембриджского университета. ISBN 978-0-521-26657-4. OCLC 10697247.
- Фогель, Стивен (1988). Устройства жизни: физический мир животных и растений. Принстон, Нью-Джерси: Издательство Принстонского университета. ISBN 978-0-691-08504-3. OCLC 18070616.
- Специфический
внешние ссылки
- Размеры организмов: площадь поверхности: соотношение объемов
- Национальная координационная группа по лесным пожарам: отношение площади поверхности к объему
- Предыдущая ссылка не работает, ссылки есть в этом документе, PDF
дальнейшее чтение
- О том, чтобы быть правильным размером, Дж.Б.С. Холдейн
Один из важнейших инженерных приемов. Отношение объема к площади поверхности любого физического тела = Отношение массы (веса) или запасенного тепла к поверхности опоры, излучения или теплообмена = Отношение инерции тела к площади поперечного сечения или площади сопротивления и т.д.
Суть вопроса в том, что V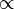
Представьте себе куб с длиной грани (ребра) 1 метр (1 сантиметр, 1 фут, 1 дюйм или 1 «чего Вам угодно»), далее единицей пусть будет метр — для простоты. Объем этого куба равен 1 м3. Каждая сторона имеет площадь1 м2, а вся площадь поверхности этого кубика равна 6 м2 — сторон-то шесть. Отношение объема к площади поверхности равно 1:6 = 1/6 (размерность в отношении,естественно, исчезает).
- Тепрь представьте себе куб со стороной 3 м.Объем этого куба равен 27 м3 (3х3х3). Каждая сторона имеет площадь 9 м2 , а вся площадь поверхности этого кубика равна 54 м2. Отношение объема к площади поверхности равно 27:54 = 1/2 = 3/6.
- То есть, при росте линейного размера в 3 раза площадь поверхности выросла в 9 раз, но объем вырос в 27 раз. Отношение объема к площади поверхности выросло в 3 раза.
- В таблице ниже приведены расчеты для кубов при пошаговом удвоении линейного размера. :
Таблица. Сравнение динамик площади поверхности и объема физического тела с ростом линейного размера.
| Линейный размер (м) |
Площадь поверхности (м2) |
Объем (м3) |
Отношение объема |
|
1 |
6,00 |
1,00 |
0,17 |
|
2 |
24,00 |
8,00 |
0,33 |
|
4 |
96,00 |
64,00 |
0,67 |
|
8 |
384,00 |
512,00 |
1,33 |
|
16 |
1 536,00 |
4 096,00 |
2,67 |
|
32 |
6 144,00 |
32 768,00 |
5,33 |
|
64 |
24 576,00 |
262 144,00 |
10,67 |
|
128 |
98 304,00 |
2 097 152,00 |
21,33 |
|
256 |
393 216,00 |
16 777 216,00 |
42,67 |
|
512 |
1 572 864,00 |
134 217 728,00 |
85,33 |
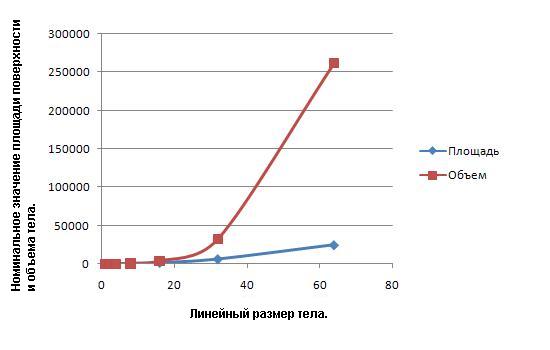
При росте линейного размера объем возрастает намного быстрее, чем площадь поверхности тела, поскольку объем пропорционален кубу линейного размера, а площадь — квадрату. Этот факт применим не только к телам кубической формы, но и к любым другим телам, естественно при сохранении формы ( или пропорций, если Вам так больше нравится).
Рисунок. Сравнение динамик площади поверхности и объема физического тела с ростом линейного размера. Минимальным отношением объема к площади поверхности, очевидно, обладает сфера 
Некоторые житейские примеры важности рассматриваемого факта.
- 1) Теплоотдача пропорциональна площади поверхности. Теплоемкость — объему тела. Из этого факта напрямую следует, что более крупное здание (той же формы) будет дольше отдавать накопленное за световой день тепло (или нагреваться днем) и потребует меньше энергии на единицу полезной площади — ! полезная площадь прямо пропорциональна внутреннему объему ! — на отопление (кондиционирование).
- 2) Масса (вес) пропорциональна объему опоры. Нагрузка на грунт — площади поверхности. Из этого факта напрямую следует, что для опоры любой формы существует размер, начиная с которого (при сохранении формы) она уйдет в любой грунт.
- 3) Ребенок имеет совершенно другое соотношение площадь/объем, чем взрослый человек. Поэтому риски переохлаждения или получения теплового удара для ребенка несоизмеримо выше (что, конечно, отчасти компенсируется другой скоростью обменных процессов у детей).
отношение площади поверхности к объему или же SA: V, — это площадь поверхности организма, деленная на его объем.
Предположим, что вы сферическая клетка. затем
# «SA» = 4πr ^ 2 # а также #V = 4 / 3πr ^ 3 # а также
# («SA») / «V» = (отмена (4πr²)) / (отмена («4πr²») × r / 3) = 3 / r #
Это говорит о том, что чем больше вы получаете (#р# увеличивается), тем меньше площадь поверхности у вас для вашего размера.
Это важно, если вы зависите от диффузии через клеточную стенку для получения кислорода, воды и пищи и избавления от углекислого газа и отходов.
Когда вы становитесь больше, веществам становится все труднее распространяться в ваш центр и из него.
Затем вы должны либо разделить на две меньшие клетки или изменить свою форму.
Вы можете быть длинными и худыми, как нервные клетки
или плоский, как эритроцит.
Если вы большая растительная клетка, у вас может развиться большая центральная вакуоль, которая подталкивает ваши органеллы ближе к вашей клеточной стенке, где они могут получить лучший доступ к ресурсам.
Если вы большой многоклеточный организм, похожий на человека, вам нужно будет разработать сложные транспортные системы, такие как легкие и кровеносные сосуды, для переноса веществ во внутренние части вашего тела.
Тема 2.
Геометрия в пространстве (стереометрия)
2
.
16
Отношение площадей поверхностей и отношение объемов тел
Вспоминай формулы по каждой теме
Решай новые задачи каждый день
Вдумчиво разбирай решения
ШКОЛКОВО.
Готовиться с нами — ЛЕГКО!
Подтемы раздела
геометрия в пространстве (стереометрия)
Решаем задачи
Во сколько раз уменьшится объем конуса, если радиус его основания останется прежним, а высота уменьшится в 3
раза?
Показать ответ и решение
Пусть площадь основания конуса равна а его высота равна
Тогда объём конуса равен
Если высота уменьшится в 3 раза, то объем конуса станет равен
Тогда объем конуса уменьшится в 3 раза.
Во сколько раз увеличится площадь поверхности шара, если радиус шара увеличить в 2 раза?
Показать ответ и решение
Пусть — изначальный радиус шара. Площадь поверхности шара вычисляется по формуле
После увеличения радиуса шара в 2 раза площадь поверхности равна
Это в 4 раза больше, чем изначальная площадь поверхности.
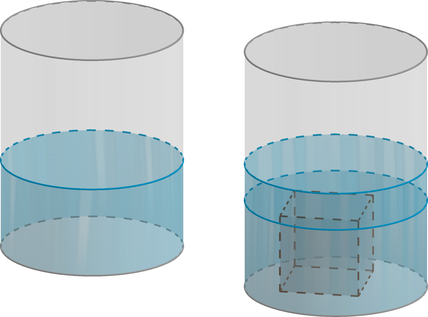
В сосуд цилиндрической формы, объем которого 2400 см, налили жидкость, заполнив сосуд
на треть, а затем в жидкость полностью погрузили некоторый предмет, вследствие чего
уровень жидкости в сосуде поднялся на четверть. Найдите объем предмета в кубических
сантиметрах.
Показать ответ и решение
Объем цилиндра вычисляется по формуле , где
– радиус основания,
– высота. Таким
образом, во сколько раз увеличивается/уменьшается высота цилиндра, во столько же раз
увеличивается/уменьшается объем цилиндра.
Следовательно, если жидкость заполнила сосуд лишь на треть, то есть высота жидкости в 3 раза
меньше высоты сосуда, то и объем жидкости в 3 раза меньше объема сосуда, следовательно, объем
жидкости равен см
.
Так как после погружения в жидкость предмета уровень повысился на четверть, то и занимаемый в
сосуде объем повысился на четверть.
Закон Архимеда гласит, что объем вытесненной жидкости равен объему погруженного в нее предмета.
Следовательно, объем предмета равен четверти объема жидкости, то есть см
.
В цилиндрическом сосуде уровень жидкости достигает см. На какой
высоте будет находиться уровень жидкости, если её перелить во второй
цилиндрический сосуд, диаметр которого в раза больше диаметра первого?
Ответ дайте в сантиметрах.
В цилиндрическом сосуде уровень воды достигает 384 см. На какой высоте будет находиться уровень воды, если её перелить во
второй цилиндрический сосуд, диаметр которого в 8 раз больше диаметра первого? Ответ дайте в сантиметрах.
Показать ответ и решение
Пусть уровень воды в первом цилиндрическом сосуде равен см, а во втором —
см.
Пусть диаметр первого сосуда равен см. Тогда площадь дна этого сосуда равна
Значит, объем воды в сосуде равен
По условию диаметр второго сосуда равен см. Тогда площадь его дна равна
Так как количество воды не изменилось, то
Тогда искомый уровень воды равен
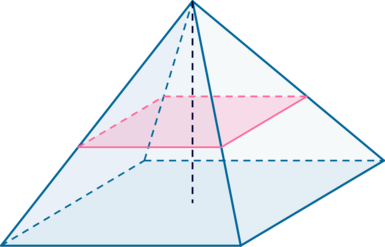
В правильной четырехугольной пирамиде с высотой через точку на боковом ребре, лежащую на расстоянии
от плоскости
основания, проведена плоскость, параллельная плоскости основания, которая отсекает от пирамиды меньшую пирамиду. Найдите
объем полученной меньшей пирамиды, если объем исходной пирамиды равен 54.
Показать ответ и решение
Также отсюда следует, что .
, следовательно,
Таким образом, объемы маленькой и большой пирамид относятся как
Следовательно, объем маленькой пирамиды равен
Радиус первого шара в 5 раз больше радиуса второго шара. Во сколько раз площадь поверхности второго шара меньше площади
поверхности первого шара?
Показать ответ и решение
Площадь поверхности шара радиуса ищется по формуле
Следовательно, площадь поверхности первого шара
относится к площади поверхности второго шара как
Так как радиус первого шара больше радиуса второго шара в 5 раз, то Следовательно,
Тогда площадь поверхности второго шара в 25 раз меньше площади поверхности первого.
Сосуд имеет форму конуса и вмещает в себя 2700 мл жидкости. Определите, сколько мл жидкости
налито в сосуд, если высота жидкости в 3 раза меньше высоты сосуда.
Показать ответ и решение
Тогда объем налитой жидкости к объему всего сосуда относится как
Следовательно объем жидкости равен
В сосуд, имеющий форму конуса, налили 75 грамм жидкости до половины высоты сосуда. Сколько
грамм этой же жидкости нужно долить в сосуд, чтобы заполнить его доверху?
Показать ответ и решение
так
как по условию высота жидкости в два раза меньше высоты сосуда. Тогда для жидкости
имеем:
Следовательно, весь сосуд вмещает этой же жидкости
Значит, долить нужно
Заметим, что в данной задаче использование плотности – чистая формальность.
Объем первого прямоугольного параллелепипеда равен 105. Найдите объем второго прямоугольного
параллелепипеда, если известно, что высота первого параллелепипеда в 7 раз больше высоты второго,
ширина второго в 2 раза больше ширины первого, а длина первого в 3 раза больше длины
второго.
Объем первого цилиндра равен 16, причем известно, что его радиус в 7 раз меньше радиуса второго цилиндра, а высота второго
цилиндра в 8 раз меньше высоты первого. Найдите объем второго цилиндра.
Показать ответ и решение
Объем цилиндра с высотой и радиусом основания
ищется по формуле
Тогда объем первого относится к объему
второго цилиндра как
Из условия следует, что
следовательно,
Площадь боковой поверхности первого цилиндра равна . Найдите площадь боковой поверхности
второго цилиндра, если его радиус в 4 раза больше радиуса первого, а высота в 5 раз меньше высоты
первого цилиндра.
Площадь боковой поверхности первого конуса относится к площади боковой
поверхности второго конуса как Найдите отношение образующей первого
конуса к образующей второго конуса, если радиус первого конуса относится к
радиусу второго как
Показать ответ и решение
Площадь боковой поверхности конуса с образующей и радиусом основания
ищется по формуле
Тогда площадь бок.
поверхности первого конуса относится к площади бок. поверхности второго как
Так как радиус первого конуса относится к радиусу второго как то есть
то
Следовательно,
Даны два конуса. Радиус второго конуса в 3 раза больше радиуса первого конуса, а высота второго конуса в 6 раз меньше высоты
первого конуса. Найдите объем первого конуса, если объем второго конуса равен 18.
Показать ответ и решение
Объем конуса с высотой и радиусом основания
вычисляется по формуле
Следовательно, объем первого конуса
относится к объему второго конуса как
Так как радиус второго в 3 раза больше радиуса первого, то Так как высота второго в 6 раз меньше высоты первого,
то Следовательно,
Объем первого шара равен равен 54. Найдите объем второго шара, если его радиус в 3 раза меньше радиуса первого
шара.
Показать ответ и решение
Объем шара радиуса ищется по формуле
Следовательно, объем первого шара относится к объему второго
как
Так как радиус второго шара в 3 раза меньше радиуса первого шара, то следовательно,
Во сколько раз радиус первого шара больше радиуса второго шара, если объем первого шара в 343 раза больше объема второго
шара?
Показать ответ и решение
Объем шара радиуса ищется по формуле
Следовательно, объем первого шара относится к объему второго
как
Значит,
Следовательно, радиус первого шара в 7 раз больше радиуса второго шара.
Радиус первого шара равен 6, а радиус второго шара равен 2. Во сколько раз объем первого шара больше объема второго
шара?
Показать ответ и решение
Объем шара радиуса ищется по формуле
Следовательно, объем первого шара относится к объему второго
как
Следовательно, объем первого шара в 27 раз больше объема второго шара.
Показать ответ и решение
Пусть – объём шара, ограниченного первой сферой. Так как радиус
в два раза больше, чем
радиус , то
.
следовательно, .