Как найти углы прямоугольного треугольника
- Главная
- /
- Математика
- /
- Геометрия
- /
- Как найти углы прямоугольного треугольника
Чтобы найти углы прямоугольного треугольника воспользуйтесь нашим очень удобным онлайн калькулятором:
Онлайн калькулятор
Чтобы найти острые углы прямоугольного треугольника вам нужно знать следующие параметры (либо-либо):
- для угла α:
- угол β
- длины катетов a и b
- длину гипотенузы (с) и длину одного из катетов
- для угла β:
- угол α
- длины катетов a и b
- длину гипотенузы (с) и длину одного из катетов
Введите их в соответствующие поля и получите результат.
Найти угол α зная угол β и наоборот
Если ∠β = , то ∠α =
0
Если ∠α = , то ∠β =
0
Формула
α = 90° — β
β = 90° — α
Найти углы прямоугольного треугольника зная катеты
Катет a =
Катет b =
∠α =
0
∠β =
0
Чему равны острые углы (α и β) прямоугольного треугольника если известны оба катета (a и b)?
Формулы
или так:
α = arctg(a/b)
β = arctg(b/a)
Пример
Для примера определим чему равны углы α и β в градусах если катет a = 5 см, а катет b = 2 см:
∠α = arctg(5/2) = arctg(2.5) ≈ 68.2°
∠β = arctg(2/5) = arctg(0.4) ≈ 21.8°
Найти углы прямоугольного треугольника по катету и гипотенузе
Гипотенуза c =
Катет =
∠α =
0
∠β =
0
Чему равны острые углы (α и β) прямоугольного треугольника если известны гипотенуза c и один из катетов (a или b)?
Формулы
sin(α) = a/c
sin(β) = b/c
cos(α) = b/c
cos(β) = a/c
или так:
α = arcsin(a/c) = arccos(b/c)
β = arcsin(b/c) = arccos(a/c)
Пример
Для примера определим чему равны углы α и β в градусах если гипотенуза c = 6 см, а катет b = 3 см:
∠α = arccos(3/6) = arccos(0.5) = 60°
∠β = arcsin(3/6) = arcsin(0.5) = 30°
См. также
Как найти острый угол в прямоугольном треугольнике
Прямоугольный треугольник, вероятно, — одна из самых известных, с исторической точки зрения, геометрических фигур. Пифагоровым «штанам» конкуренцию может составить лишь «Эврика!» Архимеда.

Вам понадобится
- — чертеж треугольника;
- — линейка;
- — транспортир.
Инструкция
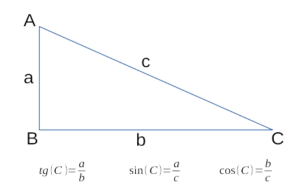
Как правило, вершины углов треугольника обозначаются заглавными латинскими буквами (A, B, C), а противоположные им стороны маленькими латинскими буквами (a, b, c) или по названиям вершин треугольника, образующих эту сторону (AC, BC, AB).
Сумма углов треугольника составляет 180 градусов. В прямоугольном треугольнике один угол (прямой) всегда будет 90 градусов, а остальные острыми, т.е. меньше 90 градусов каждый. Чтобы определить, какой угол в прямоугольном треугольнике является прямым, измерьте с помощью линейки стороны треугольника и определите наибольшую. Она называется гипотенуза (AB) и располагается напротив прямого угла (C). Остальные две стороны образуют прямой угол и называются катетами (AC, BC).
Когда определили, какой угол является острым, вы можете либо измерить величину угла при помощи транспортира, либо рассчитать с помощью математических формул.
Чтобы определить величину угла с помощью транспортира, совместите его вершину (обозначим ее буквой А) с специальной отметкой на линейке в центре транспортира, катет АС должен совпадать с ее верхним краем. Отметьте на полукруглой части транспортира точку, через которую проходит гипотенуза AB. Значение в этой точке соответствует величине угла в градусах. Если на транспортире указаны 2 величины, то для острого угла нужно выбирать меньшую, для тупого — большую.
Величину угла можно рассчитать, сделав несложные математические вычисления. Вам понадобится знание основ тригонометрии. Если известны длина гипотенузы AB и катета ВС, вычислите значение синуса угла А: sin (A) = BC / AB.
Полученное значение найдите в справочных таблицах Брадиса и определите какому углу соответствует полученное числовое значение. Этим методом пользовались наши бабушки.
В наше время достаточно взять калькулятор с функцией вычисления тригонометрических формул. Например, встроенный калькулятор Windows. Запустите приложение «Калькулятор», в пункте меню «Вид» выберете пункт «Инженерный». Вычислите синус искомого угла, например, sin (A) = BC/AB = 2/4 = 0.5
Переключите калькулятор в режим обратных функций, кликнув по кнопке INV на табло калькулятора, затем кликните по кнопке расчета функции арксинуса (на табло обозначена, как sin в минус первой степени). В окошке расчета появится следующая надпись: asind (0.5) = 30. Т.е. значение искомого угла — 30 градусов.
Источники:
- Таблицы Брадиса (синусы, косинусы)
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Обновлено 08.05.2021
Содержание
- Свойства острых углов в прямоугольном треугольнике
- Как найти острый угол в прямоугольном треугольнике
- Определение синуса, косинуса, и тангенса острого угла прямоугольного треугольника
Свойства острых углов в прямоугольном треугольнике
Острый угол в прямоугольном треугольнике — угол,
градусная мера которого менее 90º.
- Если известны 2 угла: чтобы найти острый угол надо из 90º
вычесть известный угол. - Катет прямоугольного треугольника, лежащий против острого угла в 30º,
равен половине гипотенузы. - Если в прямоугольном треугольнике острые углы равны, значит и катеты равны.
Как найти острый угол в прямоугольном треугольнике
- Если известны 2 угла: чтобы найти острый угол надо из 90º
вычесть известный угол. - Если известны катет a и катет b: чтобы найти острый угол надо
использовать формулу тангенса. - Если известна гипотенуза c и катет a: чтобы найти острый угол надо
использовать формулу синуса. - Если известна гипотенуза c и катет b: чтобы найти острый угол надо
использовать формулу косинуса.
Определение синуса, косинуса, и тангенса острого угла прямоугольного треугольника
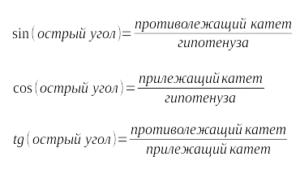
Синусом острого угла прямоугольного треугольника называется
отношение противолежащего этому углу катета к гипотенузе.
Косинусом острого угла прямоугольного треугольника называется
отношение прилежащего к этому углу катета к гипотенузе.
Тангенсом острого угла прямоугольного треугольника называется
отношение противолежащего этому углу катета к прилежащему катету.
Содержание:
- Определение острого угла
- Примеры решения задач с острыми углами
Определение острого угла
Определение
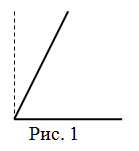
Острым углом называется угол, градусная мера которого меньше
$90^{circ}$ (рис. 1).
Все острые углы имеют градусную меру в пределах больше
$0^{circ}$ и меньше
$90^{circ}$.
Примеры решения задач с острыми углами
Пример
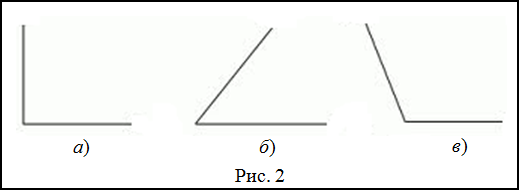
Задание. Указать острые углы на рисунке 2?
Решение. На рисунке 2 а) изображен прямой угол, так как стороны этого угла взаимно перпендикулярны,
поэтому этот угол не является острым.
Рассмотрим рисунок 2 б). На нем изображен угол, меньший, чем прямой:
А значит, по определению он является острым.
Сравнивая угол, изображенный на рисунке 2 в), с прямым, делаем вывод, что он является
тупым, так как его градусная мера больше, чем
$90^{circ}$:
Ответ. Острый угол изображен только на рисунке 2 б).

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Известно, что один из смежных углов на
$30^{circ}$ больше другого. Найти острый из этих углов.
Решение. Пусть $x^{circ}$ — меньший угол, тогда
$(x+30)^{circ}$ — больший. Так как сумма смежных углов равна
$180^{circ}$, то имеем уравнение
$$x+(x+30)=180 Rightarrow 2 x=150 Rightarrow x=75^{circ} < 90^{circ}$$
Ответ. $75^{circ} lt 90^{circ}$
Читать дальше: что такое тупой угол.
Загрузить PDF
Загрузить PDF
В геометрии угол — это фигура, которая образована двумя лучами, которые выходят из одной точки (она называется вершиной угла). В большинстве случаев единицей измерения угла является градус (°) — помните, что полный угол или один оборот равен 360°. Найти значение угла многоугольника можно по его типу и значениям других углов, а если дан прямоугольный треугольник, угол можно вычислить по двум сторонам. Более того, угол можно измерить с помощью транспортира или вычислить с помощью графического калькулятора.
-
1
Сосчитайте число сторон многоугольника. Чтобы вычислить внутренние углы многоугольника, сначала нужно определить, сколько у многоугольника сторон. Обратите внимание, что число сторон многоугольника равно числу его углов.[1]
- Например, у треугольника 3 стороны и 3 внутренних углов, а у квадрата 4 стороны и 4 внутренних углов.
-
2
Вычислите сумму всех внутренних углов многоугольника. Для этого воспользуйтесь следующей формулой: (n — 2) x 180. В этой формуле n — это количество сторон многоугольника. Далее приведены суммы углов часто встречающихся многоугольников:[2]
- Сумма углов треугольника (многоугольника с 3-мя сторонами) равна 180°.
- Сумма углов четырехугольника (многоугольника с 4-мя сторонами) равна 360°.
- Сумма углов пятиугольника (многоугольника с 5-ю сторонами) равна 540°.
- Сумма углов шестиугольника (многоугольника с 6-ю сторонами) равна 720°.
- Сумма углов восьмиугольника (многоугольника с 8-ю сторонами) равна 1080°.
-
3
Разделите сумму всех углов правильного многоугольника на число углов. Правильный многоугольник это многоугольник с равными сторонами и равными углами. Например, каждый угол равностороннего треугольника вычисляется так: 180 ÷ 3 = 60°, а каждый угол квадрата находится так: 360 ÷ 4 = 90°.[3]
- Равносторонний треугольник и квадрат — это правильные многоугольники. А у здания Пентагона (Вашингтон, США) и дорожного знака «Стоп» форма правильного восьмиугольника.
-
4
Вычтите сумму всех известных углов из общей суммы углов неправильного многоугольника. Если стороны многоугольника не равны друг другу, и его углы также не равны друг другу, сначала сложите известные углы многоугольника. Теперь полученное значение вычтите из суммы всех углов многоугольника — так вы найдете неизвестный угол.[4]
- Например, если дано, что 4 угла пятиугольника равны 80°, 100°, 120° и 140°, сложите эти числа: 80 + 100 + 120 + 140 = 440. Теперь вычтите это значение из суммы всех углов пятиугольника; эта сумма равна 540°: 540 — 440 = 100°. Таким образом, неизвестный угол равен 100°.
Совет: неизвестный угол некоторых многоугольников можно вычислить, если знать свойства фигуры. К примеру, в равнобедренном треугольнике две стороны равны и два угла равны; в параллелограмме (это четырехугольник) противоположные стороны равны и противоположные углы равны.
Реклама
-
1
Помните, что в любом прямоугольном треугольнике один угол всегда равен 90°. Это так, даже если прямой угол никак не отмечен или его значение не указано. Таким образом, один угол прямоугольного треугольника всегда известен, а другие углы можно вычислить с помощью тригонометрии.[5]
-
2
Измерьте длину двух сторон треугольника. Самая длинная сторона прямоугольного треугольника называется гипотенузой. Прилежащая сторона это сторона, которая находится возле неизвестного угла. Противолежащая сторона — это сторона, которая находится напротив неизвестного угла. Измерьте две стороны, чтобы вычислить неизвестные углы треугольника.[6]
Совет: воспользуйтесь графическим калькулятором, чтобы решить уравнения, или найдите онлайн-таблицу со значениями синусов, косинусов и тангенсов.
-
3
Вычислите синус угла, если вам известны противолежащая сторона и гипотенуза. Для этого подставьте значения в уравнение: sin(x) = противолежащая сторона ÷ гипотенуза. Например, противолежащая сторона равна 5 см, а гипотенуза равна 10 см. Разделите 5/10 = 0,5. Таким образом, sin(x) = 0,5, то есть x = sin-1 (0,5).[7]
- Если у вас есть графический калькулятор, введите 0,5 и нажмите клавишу sin-1. Если у вас нет такого калькулятора, используйте онлайн-таблицу, чтобы найти значение угла. В нашем примере угол равен 30°.
-
4
Вычислите косинус угла, если вам известны прилежащая сторона и гипотенуза. Для этого подставьте значения в уравнение: cos(x) = прилежащая сторона ÷ гипотенуза. Например, прилежащая сторона равна 1,67 см, а гипотенуза равна 2 см. Разделите 1,67/2 = 0,83. Таким образом, cos(x) = 0,83, то есть x = cos-1 (0,83).[8]
- Если у вас есть графический калькулятор, введите 0,83 и нажмите клавишу cos-1. Если у вас нет такого калькулятора, используйте онлайн-таблицу, чтобы найти значение угла. В нашем примере угол равен 33,6°.
-
5
Вычислите тангенс угла, если вам известны противолежащая и прилежащая стороны. Для этого подставьте значения в уравнение: tg(x) = противолежащая сторона ÷ прилежащая сторона. Например, противолежащая сторона равна 75 см, а прилежащая сторона равна 75 см. Разделите 75/100 = 0,75. Таким образом, tg(x) = 0,75, то есть x = tg-1 (0,75).[9]
- Если у вас есть графический калькулятор, введите 0,75 и нажмите клавишу tg-1. Если у вас нет такого калькулятора, используйте онлайн-таблицу, чтобы найти значение угла. В нашем примере угол равен 36,9°.
Реклама
Советы
- Названия углов соответствуют их значениям. Угол в 90° — это прямой угол. Угол в 180° — это развернутый угол. Угол, который лежит между 0° и 90° — это острый угол. Угол, который лежит между 90° и 180° — это тупой угол. Угол, который лежит между 180° и 360° — это невыпуклый угол.
- Если сумма двух углов равна 90°, они называются дополнительными. Запомните: два острых угла прямоугольного треугольника всегда являются дополнительными. Если же сумма двух углов равна 180°, они называются смежными.
Реклама
Об этой статье
Эту страницу просматривали 238 090 раз.