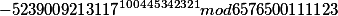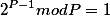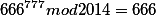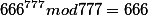Остаток числа в степени по модулю
| Основание степень и модуль, разделенные хотя бы одним пробелом |
Рассмотрим одну из задач часто встречающейся в арифметике и теории чисел, которую можно выразить несколькими примерами.
Какой остаток будет у следующих чисел
если их попытаться разделить на число 31?
И если первый пример можно решить на калькуляторе, так сказать » в лоб, не думая», то как Вы будете решать третий пример, это для некоторых очень не тривиальная задача.
Что же такое остаток? Остаток в данном случае — это такое число(по абсолютному значению меньше модуля!), отняв которое из исходного числа, полученный результат будет делится нацело на модуль ( в нашем примере модуль это число 31)
То есть, если обозначим остаток буквой Х получим (в первом примере ) что число 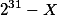
Или в другой, записи более привычной
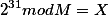
Как же решать подобные задачи?
Для этого нам надо знать несколько свойств из теории чисел, которые покажем на втором примере
1.
Даже объяснять неохота, выносим -1 за «скобки» ( отдельным множителем) и можем сразу посчитать. Если степень числа (321) четная то результат равен 1, если нечетная то -1.
2.
Если число можно представить в виде двух и более сомножителей то, остаток от этого числа будет равен произведению остатков от сомножителей по этому же модулю.
3.
Прибавив или отняв от любого сомножителя целое количество модуля — остаток не изменится.
4.
Тоже ничего сложного, просто преобразовали степень. Обычное свойство степеней.
5.
Здесь мы возвели -5 в куб и воспользовались 3 правилом, прибавив к нему 4 раза модуль
6.
Воспользовавшись первым правилом, получили что наш ответ 1
То есть можем утверждать что 
7. Последнее правило гласит, что формально, всегда существует два остатка и они равноценны. В нашем примере это 1 и -30, так как 
Надеюсь это небольшой пример разбора, дал Вам методику решения подобных задач.
А бот, который создан, поможет Вам легко узнавать правильность решения подобных задач или, если Вы преподаватель, легко и точно генерировать задачи для учеников.
Синтакис для XMPP клиентов
modul число степень модуль
число — отрицательное или положительное, целое число
степень — только положительная целая степень.
модуль — положительное целое число.
каждый элемент может содержать до 19 цифр ( вообще я не знаю на какой длине, могут возникнуть ошибки, но при (до) 19 символах все работает хорошо)
поэтому нет ничего страшного найти остаток вот от такого «монстра»
кто хочет может умножать на калькуляторе 
ответ 3848922529426
Если же Вы вдруг нашли ошибку или у Вас есть пожелания или вопросы, не стесняйтесь обращайтесь Обратная связь с разработчиками бота.
Интересные факты
Утверждается, что если P — число простое то выполняется вот такое равенство
Это условие необходимое(то есть применимо ко всем простым числам) но не достаточное ( то есть есть составные числа для которых эта формула тоже действительна)
Красивое выражение было найдено пока тестировал бота ( для 2014 года) 
На 31 мая 2018 года еще нашлось кое что интересное
Смотрите
Удачных расчетов!
vorvalm писал(а):
Masterov писал(а):
vorvalm писал(а):
[math]a^{varphi(m)}equiv 1pmod m[/math]
Мне эта запись непонятна.
Я много раз её в Википедии встречал,
но никто её определения не дает.
Это азы теории чисел. Смотрите не Википедию, но А.А.Бухштаба. Это означает:
[math]a^{varphi(m)}-1=km[/math]
1. Если в Википедии это понятие встречается, а нигде это не поясняется (в Википедии), то это — не правильно.
2. Я имею очень неплохую подготовку прикладного математика по специальности «нелинейная динамика». На форуме опубликована моя монография, где изложены три метода (два — авторские) анализа нелинейных моделей в интегральной форме записи (нелинейные интегро-дифференциальные уравнения). Я имею математическую подготовку, которой могут позавидовать многие физики, но даже я не знаю, что означает запись:
[math]a^{varphi(m)}equiv 1pmod m[/math]
Если я не понимаю этой записи, то (очевидно) её не понимают большинство физиков.
(Проверьте сами.)
Я это говорю к тому, что математики (и не только математики, но математики — особенно) выдумывают понятия и записи, которые понятны только им. А потом жонглируют ими и раздувают щёки, дескать — вот мы какие умные, нас даже не понимают.
Физики тоже так делают. (Выдумывают жаргонные словечки, а потом ими публично жонглируют.)
Всё это делает бездари, чтобы создать видимость научной деятельности.
На то, чтобы придумать что-то полезное людям, у них просто не хватает потенции учёного.
Последний раз редактировалось Masterov 19 дек 2014, 20:54, всего редактировалось 2 раз(а).
В украинской (также как и в английской и немецкой [остальные не проверял]) версии википедии есть хороший пример использования Теоремы Эйлера:
Наприклад ми хочемо обчислити 7222 (mod 10). Маємо, що 7 і 10 є
взаємно простими іφ(10) = 4. Одже згідно з теоремою Ейлера 74 ≡ 1 (mod 10) і як наслідок7222 ≡ 74×55 + 2 ≡ (74)55 x 72 ≡ 155 x 72 ≡ 49 ≡ 9 (mod 10).
Моя попытка перевода:
Например мы хотим вычислить «7222 (mod 10)». 7 и 10 являются взаимно-простыми и φ(10) = 4 (это число натуральных чисел не больших чем 10 и являющихся взаимнопростыми по отношению к 10. Это следующие числа: 1,3,7,9 и всего их 4).
Следовательно согласно теореме Эйлера 74 ≡ 1 (mod 10) и как следствие:
7222 ≡ 74×55 + 2 ≡ (74)55 x 72 ≡ 155 x 72 ≡ 49 ≡ 9 (mod 10).
Следствия из теоремы:
если aφ(n) ≡ 1 (mod n), то и (aφ(n))k ≡ 1 (mod n) для любого положительного k, т.к.
(aφ(n))k ≡ aφ(n) mod n * (aφ(n))k — 1 mod n ≡ (aφ(n))k — 1 (mod n) и т.д.
Я думаю, что «в виде исключения» здесь можно изложить полное решение. Сам пример составлен достаточно удачно, и на его основе можно пронаблюдать разные «тонкости», касающиеся того, какие методы можно применять. Способы хотя и стандартны, но некоторыми из них пример решается легче, а некоторыми сложнее. К тому же, примеры этого типа часто звучат на форуме, и написанное потом можно будет давать в качестве ссылки.
Но, тем не менее, даже для понимания решения нужно владеть следующим «теорминимумом»: линейные сравнения и их системы; китайская теорема об остатках; малая теорема Ферма; функция Эйлера; теорема Эйлера. Всё это можно прочитать, например, в учебнике Бухштаба.
Прежде всего, нужно разложить на простые множители число $%611$%. Если бы оно было простым, ответ мгновенно получался бы из малой теоремы Ферма: $%x^pequiv xpmod{p}$%. Но здесь число составное: деля его последовательно на простые, видим, что оно делится на $%13$% и равно $%pq=13cdot47=611$%.
Понятно, что число $%a=34$% не делится ни на $%p$%, ни на $%q$%, поэтому оно взаимно просто с $%n=pq$%, и можно применить теорему Эйлера: $%a^{varphi(n)}equiv1pmod{n}$%. Здесь $%varphi(n)=varphi(pq)=(p-1)(q-1)$%; показатель степени приводим по модулю $%varphi(n)$%, получая $%pq-(p-1)(q-1)=p+q-1=59$%. При этом задача сводится к нахождению остатка от деления $%34^{59}$% на $%611$%. В таком виде можно было бы посчитать остаток при помощи «быстрого возведения в степень», последовательно возводя числа в квадрат и беря остатки от деления. Далее через двоичное разложение $%59$% мы получили бы ответ, но это требовало бы длинных вычислений. Тем не менее, сам этот метод иногда применим, и его полезно иметь в виду. Здесь же проще найти остатки от деления числа на $%13$% и $%47$% по отдельности, а потом применить китайскую теорему об остатках.
Итак, по модулю $%p=13$% мы заменяем $%34$% на $%-5$%, а показатель степени $%pq$% приводим по модулю $%p-1=12$%, получая $%q=47$%, что сравнимо с $%-1$%. Это удобно, так как вместо возведения в степень нужно найти элемент, обратный $%-5$% по модулю $%13$%. Это делается устно за счёт того, что $%5cdot5equiv25equiv-1pmod{13}$%, то есть число $%x=34^{611}$% из условия при делении на $%13$% даёт в остатке $%5$%. Более подробно повторим то, что было выше: $%xequiv(-5)^{611}equiv(-5)^{12q-1}equiv(-5)^{-1}equiv5pmod{13}$%.
Теперь рассуждаем по модулю $%q=47$%. Здесь основание степени приводим по модулю $%47$%, заменяя на $%-13$%, а показатель приводим по модулю $%q-1=46$%, заменяя на $%13$%. Получается $%xequiv(-13)^{13}pmod{47}$%, и здесь уже применяем быстрое возведение в степень:
$%(-13)^2equiv169equiv28equiv-19pmod{47}$%;
$%(-13)^4equiv(-19)^2equiv361equiv32equiv-15pmod{47}$%;
$%(-13)^8equiv(-15)^2equiv225equiv37equiv-10pmod{47}$%.
Наконец, $%(-13)^{13}equiv(-13)^{8+4+1}equiv(-10)(-15)(-13)equiv(-10)7equiv24pmod{47}$%.
Итак, оба остатка найдены, и остаётся решить систему из двух сравнений:
$$
left{
begin{array}{l}
xequiv5mod{13}\
xequiv24pmod{47}
end{array}
right.
$$
Это делается стандартно: из второго уравнения получаем $%x=47y+24$%, где $%y$% целое, и подставляем в первое. После упрощений получается $%-5y-2equiv5pmod{13}$%, то есть $%-5yequiv7pmod{13}$%. Домножая обе части на $%5$%, имеем $%yequiv35equiv-4pmod{13}$%, то есть $%y=13k-4$%, где $%k$% целое. Отсюда $%x=47(13k-4)+24=611k-164$%. Остаток от деления на $%611$% равен $%611-164=447$%, и это ответ.
Подсчет остатка от деления большого числа
Для проверки на всякие чек-суммы, иногда нужно делить что-то вроде 6796573475894375894375893479583745897943759830 на какой-нибудь 73 или 97.
Далеко не все языки программирования на это рассчитаны. Есть, конечно и примочки в виде классов типа BigInt и т.п., но есть способ похитрее.
(A*B) mod N = ((A mod N) * (B mod N)) mod N
(A+B) mod N = ((A mod N) + (B mod N)) mod N
Другими словами, есть представить число 43517 как 7 + 10 + 500 + 3000 + 40000, т.е. 7*10^-1 + 1 * 10^1 + 5 * 10^2 + 3 * 10^3 + 4 * 10^4, то многое упрощается.
Остаток от деления цифры это легко, а если делитель больше 9, то и вовсе равняется самой цифре.
Что же касается степеней десятки, то тут, кажется, ничего не изменилось, ведь все равно нужно посчитать остаток от деления 10000000000000000000000000000 на 73.
Ан нет! Мы знаем, что 10^2 это 10*10, 10^3 это 10*10^2, а 10^N это 10*10^(N-1),
Из этого и нашей формулы следует, что (10^N) mod M = ((10^(N-1) mod M) * 10) mod M.
Таким образом, можно этот остаток вычислять итеративно, на каждом шаге, начиная с младшей цифры и до старшей, каждый раз берем остаток из предыдущего шага, умножаем на 10 и вычисляем остаток.
Вот так можно его и посчитать.
Пример.
Остаток от деления 1275436137 на 97.
Вначале, напишем наши цифры 7 3 1 6 3 4 5 7 2 1.
Посчитаем остатки от деления степеней 10-ки на 97. (При программировании, если делитель встречается часто, лучше всего эти результаты закешировать для более быстрых расчетов, подгружая массив в память, когда это нужно.)
1 mod 97 — 1, без вопросов.
(1 * 10) mod 97 — 10
(10 * 10) mod 97 — 3
(3 * 10) mod 97 — 30
(30 * 10) mod 97 — 9
(9 * 10) mod 97 — 90
(90 * 10) mod 97 — 27
(27 * 10) mod 97 — 76. и дальше 81, 34.
Перемножаем пары, складываем. У нас все цифры имеют ровно такие же остатки, так что
7 * 1 + 3 * 10 + 1 * 3 + 6 * 30 + 3 * 9 + 4 * 90 + 5 * 27 + 7 * 76 + 2 * 81 + 1 * 34 = 1470
1470 mod 97 = 15
Ответ. 1275436137 mod 97 = 15, что можно проверить на виндошном калькуляторе.
В псевдокоде
s <- 0
a <- 1
for i = LastDigitIndex to 1
s <- s + a * digits[i]
a <- (a * 10) mod n
endfor
result <- s mod n
Остаток от деления числа в большой степени
Как можно быстро вычислить (x^n)mod y. Уже когда-то копал этот вопрос и обнаружил теорему Эйлера (теория чисел).
Не относится к вопросу: Но вся проблема в том, что я учусь в школе, и мы не проходили еще подобных выражений, найденных мною на wiki, и теории чисел. Объясните пожалуйста:
- Как использовать эту теорему на практике(например, реализация на C).
- (Не так важно, но просто интересно)Кратко значение формулировки на
wiki. Буду рад какой-нибудь статье, etc для тех, кто еще не знаком с теорией чисел и математикой >9 классов.
Наприклад ми хочемо обчислити 7 222 (mod 10). Маємо, що 7 і 10 є взаємно простими і φ(10) = 4 . Одже згідно з теоремою Ейлера 7 4 ≡ 1 (mod 10) і як наслідок
7 222 ≡ 7 4×55 + 2 ≡ (7 4 ) 55 x 7 2 ≡ 1 55 x 7 2 ≡ 49 ≡ 9 (mod 10).
Моя попытка перевода:
Например мы хотим вычислить «7 222 (mod 10)». 7 и 10 являются взаимно-простыми и φ(10) = 4 (это число натуральных чисел не больших чем 10 и являющихся взаимнопростыми по отношению к 10 . Это следующие числа: 1,3,7,9 и всего их 4 ).
Следовательно согласно теореме Эйлера 7 4 ≡ 1 (mod 10) и как следствие:
7 222 ≡ 7 4×55 + 2 ≡ (7 4 ) 55 x 7 2 ≡ 1 55 x 7 2 ≡ 49 ≡ 9 (mod 10).
Следствия из теоремы:
если a φ(n) ≡ 1 (mod n), то и (a φ(n) ) k ≡ 1 (mod n) для любого положительного k , т.к.
(a φ(n) ) k ≡ a φ(n) mod n * (a φ(n) ) k — 1 mod n ≡ (a φ(n) ) k — 1 (mod n) и т.д.
Остаток от деления больших чисел
числа по модулю образуют кольцо (а по простому — даже поле), то есть — нормальную арифметику. Модуль можно брать на любом этапе.
конечно, посчитать сначала 18^180, а потом взять (mod 13) — это долго (хотя на компе вполне реально, до нескольких миллионов знаков длинная арифметика считается несложно). Но можно брать модуль на каждом шаге!
например, 18^180 mod 13 = (18mod 13)^180 mod 13=5^180 mod 13.
теперь, как возводить в высокую степень (не обязательно по мудулю):
a^180=a^(4+16+32+128)
считаем и запоминаем промежуточные результаты
a^2=a*a
a^4=(a^2)(a^2)
a^8=(a^4)(a^4)
a^16=(a^4)(a^4)
a^32=(a^16)(a^16)
a^64=(a^32)(a^32)
a^128=(a^64)(a^64)
итого a^180=a^4 * a^16 * a^32 * a^128
если надо считать по модулю 13 — делаем каждую операцию по модулю 13, все числа — небольшие, не больше 12.
если немного подумать, то разложение a^180=a^(4+16+32+128) — это просто двоичное представление числа, 4,16,32,128 — единички, остальные — нули.


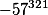
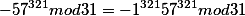
57^{321}mod31=(-1)mod31*57^{321}mod31)
^{321}mod31=-1*(-5)^{321}mod31)
^{321}mod31=-1*(-5^3)^{frac{321}{3}}mod31=-1*(-5^3)^{107}mod31)
^{107}mod31=-1*(-125)^{107}=-1*(-125+31+31+31+31)^{107}mod31)
^{107}mod31=-1*(-1)^{107}mod31=-1*-1mod31=1)