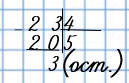Как найти остаток 4 класс по математике

1. Главная
2. Справочники
3. Справочник по математике для начальной школы
4. Деление
5. Деление с остатком

Советуем посмотреть:

Табличное деление

Внетабличное деление

Деление суммы на число

Деление на однозначное число

Деление чисел, оканчивающихся нулями

Свойства деления

Деление

Правило встречается в следующих упражнениях:

2 класс

Страница 76. Урок 29,
Петерсон, Учебник, часть 3

Страница 77. Урок 29,
Петерсон, Учебник, часть 3

Страница 79. Урок 30,
Петерсон, Учебник, часть 3

Страница 80. Урок 30,
Петерсон, Учебник, часть 3

Страница 81. Урок 31,
Петерсон, Учебник, часть 3

Страница 82. Урок 31,
Петерсон, Учебник, часть 3

Страница 84. Урок 32,
Петерсон, Учебник, часть 3

Страница 87. Урок 33,
Петерсон, Учебник, часть 3

Страница 108. Повторение,
Петерсон, Учебник, часть 3

3 класс

Страница 58. Тест 1. Вариант 1,
Моро, Волкова, Проверочные работы

Страница 33,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 34,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 35,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 32,
Моро, Волкова, Рабочая тетрадь, часть 2

Страница 63,
Моро, Волкова, Рабочая тетрадь, часть 2

Страница 71. Урок 24,
Петерсон, Учебник, часть 1

Страница 6. Урок 3,
Петерсон, Учебник, часть 2

Страница 59. Урок 24,
Петерсон, Учебник, часть 2

Страница 49. Урок 22,
Петерсон, Учебник, часть 3

4 класс

Страница 47,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 81,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 12,
Моро, Волкова, Рабочая тетрадь, часть 1

Страница 11. ПР 3. Вариант 2,
Моро, Волкова, Проверочные работы

Страница 63. ПР 2. Вариант 2,
Моро, Волкова, Проверочные работы

Страница 29,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 31,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 28,
Моро, Волкова, Рабочая тетрадь, часть 2

Страница 32. Урок 11,
Петерсон, Учебник, часть 1

Страница 34. Урок 12,
Петерсон, Учебник, часть 1

5 класс

Задание 529,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 535,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1074,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1086,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1160,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1724,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 6,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2

Задание 1,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2

Номер 769,
Мерзляк, Полонский, Якир, Учебник

Номер 801,
Мерзляк, Полонский, Якир, Учебник

6 класс

Номер 369,
Мерзляк, Полонский, Якир, Учебник

Номер 435,
Мерзляк, Полонский, Якир, Учебник

Номер 436,
Мерзляк, Полонский, Якир, Учебник

Номер 533,
Мерзляк, Полонский, Якир, Учебник

Номер 1004,
Мерзляк, Полонский, Якир, Учебник

Задание 638,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1160,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1264,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1308,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1539,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

7 класс

Номер 331,
Мерзляк, Полонский, Якир, Учебник

Номер 351,
Мерзляк, Полонский, Якир, Учебник

Номер 431,
Мерзляк, Полонский, Якир, Учебник

Номер 496,
Мерзляк, Полонский, Якир, Учебник

Номер 556,
Мерзляк, Полонский, Якир, Учебник

Номер 573,
Мерзляк, Полонский, Якир, Учебник

Номер 582,
Мерзляк, Полонский, Якир, Учебник

Номер 606,
Мерзляк, Полонский, Якир, Учебник

Номер 608,
Мерзляк, Полонский, Якир, Учебник

Номер 873,
Мерзляк, Полонский, Якир, Учебник

8 класс

Номер 47,
Мерзляк, Полонский, Якир, Учебник

Номер 138,
Мерзляк, Полонский, Якир, Учебник

Номер 141,
Мерзляк, Полонский, Якир, Учебник

Номер 193,
Мерзляк, Полонский, Якир, Учебник

Номер 212,
Мерзляк, Полонский, Якир, Учебник

Номер 241,
Мерзляк, Полонский, Якир, Учебник

Номер 302,
Мерзляк, Полонский, Якир, Учебник

Номер 304,
Мерзляк, Полонский, Якир, Учебник

Номер 305,
Мерзляк, Полонский, Якир, Учебник

Номер 306,
Мерзляк, Полонский, Якир, Учебник

Математика, 4 класс. Урок № 54

Письменное деление на двузначное число с остатком.

Перечень вопросов, рассматриваемых в теме:

— Как делить многозначное число на двузначное с остатком?

— Как ким должен быть остаток от деления?

Глоссарий по теме:

Частное – результат деления одного числа на другое.

Неполное частное – результат деления с остатком, который показывает, какое максимальное число раз делитель содержится в делимом.

Остаток – число, которое получается в результате деления с остатком и показывает, какое минимальное число нужно вычесть из делимого, чтобы полученное число делилось нацело на делитель.

Основная и дополнительная литература по теме урока (точные библиографические данные с указанием страниц):

1.Петерсон Л.Г. Математика. 4 класс. 1 ч. – М.: 2013. – стр. 31-38.

2. Математика. Учебник для 4 кл. нач. шк. В 2 ч./М.И. Моро, М.А. Бантова – М.: Просвещение, 2017.

3. Математика. 4 класс. Учебник. Часть1/ Н.Б.Истомина, Т.Н.Миракова, Т.Б.Бука. Смоленск: Ассоциация XXI век, 2012. – стр. 38-52.

4. Математика. Учебник для 4 класса нач. шк. Часть 2/А.Л.Чекин. – М.: Академкнига/Учебник, 2016. – стр. 16-20.

Теоретический материал для самостоятельного изучения

При делении с остатком на двузначное число рассуждать будем так же, как и при делении без остатка.

Разделим 444 : 54.

Первое неполное делимое — это само число, 444. Поэтому в частном будет только одна цифра. Чтобы легче было найти цифру частного, будем делить 444 не на 54, а на 50. Для этого 44 разделим на 5, получим 8. Проверим, подходит ли она: 54 · 8 = 50 · 8 + 4 · 8 = 432, а 432 < 444.

Значит, пробная цифра 8 подходит. Записываем ее в частном. Закончим запись деления столбиком. Умножаем 54 на 8, будет 432. Находим остаток от деления. Он равен 12. 12 меньше, чем 54, то есть остаток меньше делителя. На этом деление закончено. При делении числа 444 на 54 получилось частное 8 и остаток 12.

Найдём значение частного 45598 : 58.

Выделим первое неполное делимое 455 сотен. Так как деление начинаем с сотен, в частном получим 3 цифры. Ищем первую цифру частного: 45 : 5 = 9

Получаем пробную цифру 9.

58 · 9 = 522, 522 > 455

Значит, 9 не подходит.

Пробуем цифру 8. Для проверки этой цифры используем другой способ. Будем умножать десятки:

5 дес. · 8= 40 дес.

8 · 8= 6 дес.

40 + 6 дес. > 45 дес. Значит, 8 это тоже много.

Пробуем следующую цифру 7.

5 дес. · 7 = 35 дес.

В запасе ещё: 45 дес. – 35 дес. = 10 дес. Этого точно хватит, так как при умножении 8 единиц на 7 получится 5 десятков. Значит, цифра 7 подходит. Записываем её в частном.

Умножаем 58 на 7, будет 406. Вычитаем 406 из 455, будет 49. Остаток 49 меньше делителя 58.

Второе неполное делимое 499 десятков. Ищем цифру частного: 49:5=9

Получаем пробную цифру 9.

Проверяем:

5 дес. · 9 = 45 дес.

45 + 7 дес. > 49 дес. Значит, в частном должно быть меньше 9.

Проверяем 8.

50 · 8 = 400

8 · 8 = 64

400 + 64 = 464

464 < 499, значит, цифра 8 подходит. Записываем её в частном.

Умножаем 58 на 8, будет 464. Вычитаем 464 из 49, будет 3. Остаток 35 меньше делителя 58.

Третье неполное делимое 358 едини. Ищем цифру частного: 35 : 5 = 7, получаем пробную цифру 7. Проверяем, но мы уже умножали 58 на 7, получили 406. Это больше, чем 358. Значит, 7 не подходит.

Проверим 6.

50 · 6 = 300

8 · 6 = 48

300 = 48 = 348

348 < 358, значит, цифра шесть подходит. Записываем её в частном.

Умножаем 58 на 6, будет 348. Вычитаем 348 из 358, будет 10. Остаток 10 меньше делителя 58. Неполных делимых больше нет. Деление окончено. В результате получили частное 786 и остаток 10.

Задания тренировочного модуля:

1. Не выполняя вычислений, найдите пропущенное делимое с помощью первого равенства.

Правильный вариант: 902; 1279

2.Заполните таблицу.

Правильный ответ:

3. Выберите записи, которые соответствуют рисунку.

Варианты ответа:

13:4=3 (ост. 1)

17:3=5 (ост. 2)

16:5=3 (ост. 1)

3·5+1=16

5·3+1=16

16:3=5 (ост. 1)

Правильный вариант:

16:5=3 (ост. 1); 16:3=5 (ост. 1)

4. Раскрасьте карточки с выражениями, в значении частных которых будет остаток.

48:4

28:7

72:8

65:8

59:6

20:3

Правильный вариант:

65:8

59:6

20:3

План урока:

Случаи деления 80 : 20, 87 : 29

Деление с остатком

Решение задач на деление с остатком

Случаи деления, когда делитель больше делимого

Здравствуйте, ребята. Я, Знайка, продолжаю учить вас математике.

Выражение «твердый орешек» означает трудную для решения задачу. Орешек знанья тверд, но мы не привыкли отступать, вместе его расколем. Пусть скорлупа ореха — символ знания, ядро — опыт человечества. Математика раскроет тайны деления двузначных чисел, если будем стараться. Французский ученый Декарт говорил: «Умейте использовать свой хороший ум, чтобы справиться с задачами».

Начинайте, ребята, скорее работу,

Решайте, считайте, не сбивайтесь со счёта.

Случаи деления 80 : 20, 87 : 29

Начнем с деления на двузначное число.

Приемы деления вида 80 : 20

Приемы деления вида 87 : 29

Найдите значения двух выражений:

Для решения посмотрите на цифры единиц. Делитель заканчивается на 9. Вспомните таблицу умножения девяти. Какое произведение имеет семерку на конце? 27.

Других вариантов в таблице умножения на девять нет. Ответ равен трем.

Внимательно посмотрите на цифры в единицах. Делимое заканчивается на четверку. Вспомните множитель, который при умножении шести в произведении дает последнюю цифру четверку.

Это два случая: четыре, девять. В значениях произведений четверка на конце. Какой множитель подходит? Давайте посмотрим. Девять — многовато.

Задания легко решать, если знаешь таблицу умножения.

Деление столбиком на двузначное число

Вы уже знаете, что для записи действия деления применяют математический символ в виде двоеточия (∶), обелюса (÷), дробной (–), косой (∕) черты. Сегодня мы используем знак, который похож на лежащую боком букву.

При делении столбиком очень важна аккуратность, поэтому возьмите листок в клеточку.

Как записать решение примера 32 : 16 столбиком? Запишите каждую цифру делимого 32 в отдельную клеточку. Отступите одну клеточку вправо, запишите делитель 16. Проведите вертикальную и горизонтальную черточку.

Подбираем частное. Посмотрите на цифры единиц 2 и 6. Вспомните табличные случаи.

Семерка нам не подойдет, потому что 16 ∙ 7 — это большая величина. Значит, выбираем двойку. Проверяем: 16 ∙ 2 = 32. Записываем двойку на место частного под чертой. Вычитаем 32 из делимого. Пишем нуль. 32 разделили нацело.

Хорошо. А знаете ли вы, что с древних времён замечено влияние грецкого ореха на работу мозга. Как будто природа создала его, по форме извилин напоминающим полушария головного мозга. Благодаря работе этого центрального органа мы справляемся с математическими задачами.

Деление с остатком

Ребята, я предлагаю вам отправиться в путешествие по реке на лодках. Прежде чем отплыть от берега, нам нужно разделить 9 спасательных кругов на 2 лодки. Как узнать, сколько кругов окажется в одной лодке?

Верно, надо разделить. Запишите решение. Сколько получилось в выражении?

У вас трудности. Что заметили?

9 на 2 нацело не делится.

Почему не можем найти значение данного выражения?

Потому что это не табличный случай. Мы не умеем решать такие выражения.

Ребята, оказывается, в примерах может получиться остаток. Это арифметическое действие, играющее большую роль в математике и криптографии — науке о защите информации. В компьютерной технике тоже часто решают данные выражения.

Напишите отрезок натурального ряда от 17 до 37.

Выпишите из этого отрезка числа, которые делятся на 9.

Проверьте, это — 18, 27, 36.

Остаток при делении натуральных чисел 19, 28, 37 на 9 равен единице, потому что они следующие при счете.

Запишите отрезок натурального ряда от 11 до 25. Обведите числа, которые делятся на шесть нацело.

Укажите остатки при делении на 6 тринадцати и четырнадцати. Запишите выражения.

Проверьте:

Объясните, как рассуждали.

15 — на третьем месте после 12, 16 — четвертое место, а 17 – пятое место после 12.

Какой самый большой остаток получается при делении на 6?

Это пять, так как между величинами, которые делятся на шесть нацело, находится пять чисел.

Интересно знать! В Древнем Египте кушать ядра грецких орехов могли только высшие, самые главные жрецы. Для всех остальных, особенно для простого народа — это было запрещено. Чтобы не становились умнее и не начали много думать. Но мы с вами знаем пользу орехов и хорошо соображаем, поэтому продолжаем урок.

Деление с остатком на однозначное число

Существует два способа решения примеров.

1 способ деления на 5, 6, 7, 8, 9

Первый способ подходит, когда делитель равен или больше пяти. Мы должны найти в делимом наибольшее число, чтобы разделить, например, на семерку.

Как его отыскать? Посчитайте семерками. Если бы делили на пять, то считали бы пятерками, на шесть – шестерками и так далее.

Считаем семерками:

Разве 41 разделить на 7 — это пять? Нет, мы разделили только 35. Теперь найдем, сколько не разделили. Из 41 отнимите 35, получится шесть. Это искомый остаток.

Сделайте обязательный шаг — убедитесь, что остаток получился меньше чем делитель. Действительно 6 < 7. Правильное решение. Если получится больше, то нужно пересчитать заново.

Вычислите, чему равен частное и остаток при делении:

2 способ деления на 4, 3, 2 и 1

Второй способ подходит, когда делитель меньше пяти. Способ заключается в том, что делимое уменьшаем на 1 и проверяем, делится ли оно на делитель. Вы посмотрите:

Значит, вы можете применять оба способа в решении таких примеров.

Сорок пять меньше 52, а пятьдесят четыре больше. Значит, делим 45. Находим сколько осталось.

Лучше использовать второй способ. Вычитайте единицу.

Деление на двузначное число с остатком

Орешек знаний тверд, но мы его удачно раскалываем. Для решения таких примеров научимся работать не с самим числом, а с его десятками, но не с простыми, а округленными. Каким образом это работает?

Договоримся так: если количество единиц в числе меньше пяти, то есть — 1, 2, 3, 4, то количество десятков изменять не будем. Если же количество единиц в числе больше пяти, то есть — 5, 6,7, 9, то количество десятков увеличим на один.

Например, 96 разделим на 29. Каждое число округлим. У 96-и девять десятков, да шестерка даст еще один десяток. Округлим 96 до десяти десятков. 29 имеет два десятка и один десяток даст девятка, потому что она больше пяти.

Получается, что надо 10 десятков разделить на три десятка. Воспользуемся вторым способом. Уменьшим 10 на единицу, получаем 9.

Особенность в решении таких примеров в том, что не надо сразу писать ответ. Держите под рукой черновик и проверяйте решение. Чтобы проверить, не ошиблись ли, надо:

Решим следующий пример, где этот метод не работает. 77 – семь десятков да семерка в единицах дает еще один десяток. 13 округляем до десяти.

Получается, что пример сводится к делению восьми на один. Но восьмерка не подходит. 13 ∙ 7 явно больше 77. Поэтому пробуем шестерку. Видите, шестерка не подошла.

Уменьшаем еще на один. Получаем пять.

Полезно знать, что употреблять грецкие орехи нужно взрослым и детям. Важно это делать правильно и регулярно. Тогда вы получите максимальную пользу от этого ценного продукта.

Продолжим урок математики.

Деление с остатком столбиком

В 52 содержится 6 раз по 8, остаётся 4.

52 : 8 = 6 (ост. 4)

Пример с остатком запишите в виде деления в столбик:

1. Делимое 52 напишите слева, правее — делитель 8. Между ними проведите вертикальную черту в две клетки — знак деления, горизонтальной линией подчеркните делитель.
2. Сколько делителей 8 помещается в делимом 52? Вспомните табличный случай 8 ∙ 6 = 48. Запишите неполное частное 8 в форму.
3. Найдите остаток. 48 вычтите из делимого. Проведите черту. Это знак равно. Запишите 4. 

Напоминаю: сравните остаток и делитель. 4 < 6. Пример решили верно.

Выполните деления с остатком 51 : 7 =

Ближайшее к делимому будет табличное произведение 49.

2 < 7. Значит, пример решили правильно.

Проверка деления с остатком

Но случаются ошибки. Проверить решения можно обратными действиями.

Выполните деление с остатком и сделайте проверку:

Убедиться в правильности решения помогает проверка.

Сравните: 6 < 12. 

Решение задач на деление с остатком

Простые задачи легко решить, если составить модель-схему условия и решения задачи на числовом луче.

Рассмотрите пример задачи:

Повар испек 17 творожных и 19 брусничных ватрушек. На тарелки положит по три штуки одного сорта. Узнайте, сколько нужно тарелок и сколько ватрушек останется.

Решение:

Ответ: для творожных ватрушек нужно 5 тарелок, две останутся; для брусничных — 5 тарелок, одна ватрушка останется.

Составьте задачу на деление с остатком, выбрав подходящее выражение:

Проверьте рассуждение. Для задачи подойдет второе выражение, а первое и последнее – не подходят, потому что это табличные случаи.

Пример задачи: На пальто пришивается 4 пуговицы. На сколько таких пальто хватит 15 пуговиц? Сколько пуговиц останется?

Ответ: пуговиц хватит на три пальто. Останется 3 пуговицы.

Придумайте задачу к схеме:

Мама купила 21 конфету и поделила по 8 штук детям. Сколько детей в семье и сколько конфет мама оставила себе?

Решение:

21 : 8 = 2 (ост.5)

Ответ: в семье двое детей. Мама оставила 5 конфет.

Умения решать задачи по математике помогают в жизни.

Незнайка отправился в магазин. У него есть 90 рублей, и он хочет купить мороженое по цене 28 рублей. Сколько стаканчиков с мороженым сможет купить Незнайка и сколько денег у него останется?

Подсказка: решить задачу можно округлив величины. 90 – это девять десятков, а 28 округлим до трех десятков.

Проверьте:

Ответ: Незнайка купит 3 стаканчика с мороженным. У него останется 6 рублей.

Случаи деления, когда делитель больше делимого

В конце урока Орешек принес интересный пример:

Делитель 9 больше делимого 7. Как решить?

Сколько раз по девять содержится в семи? Конечно — нуль раз. В частном запишите 0. Нуль умножить на девять получится нуль. Вычитаем 0. Остаток 7.

Ребята, наш урок подошёл к концу.

Как научить ребенка делению? Самый простой метод – выучить деление столбиком. Это гораздо проще, чем проводить вычисления в уме, помогает не запутаться, не «потерять» цифры и выработать мысленную схему, которая в дальнейшем будет срабатывать автоматически….

Как проводится

Деление с остатком – это способ, при котором число нельзя разделить ровно на несколько частей. В результате данного математического действия, помимо целой части, остается неделимый кусок.

Приведем простой пример того, как делить с остатком:

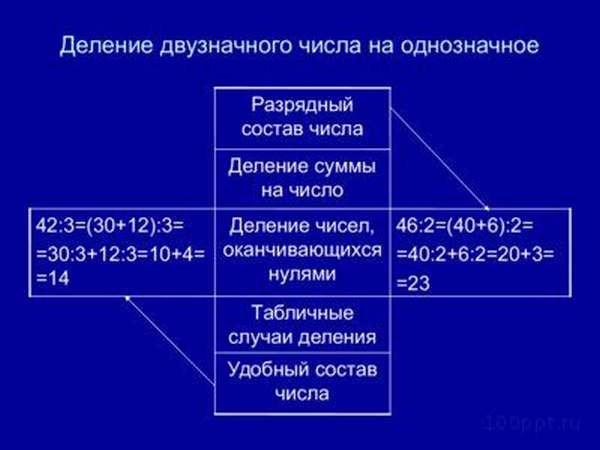
Есть банка на 5 литров воды и 2 банки по 2 литра. Когда из пяти литровой банки воду переливают в двухлитровые, в пятилитровой останется 1 литр не использованной воды. Это и есть остаток. В цифровом варианте это выглядит так:

5:2=2 ост (1). Откуда 1? 2х2=4, 5-4=1.

Теперь рассмотрим порядок деления в столбик с остатком. Это визуально облегчает процесс расчета и помогает не потерять числа.

Алгоритм определяет расположение всех элементов и последовательность действий, по которой совершается вычисление. В качестве примера, разделим 17 на 5.

Основные этапы:

1. Правильная запись. Делимое (17) – располагается по левую сторону. Правее от делимого пишут делитель (5). Между ними проводят вертикальную черту (обозначает знак деления), а затем, от этой черты проводят горизонтальную, подчеркивая делитель. Основные черты обозначена оранжевым цветом.
2. Поиск целого. Далее, проводят первый и самый простой расчет – сколько делителей умещается в делимом. Воспользуемся таблицей умножения и проверим по порядку: 5*1=5 помещается, 5*2=10 помещается, 5*3=15 помещается, 5*4=20 – не помещается. Пять раз по четыре – больше чем семнадцать, значит, четвертая пятерка не вмещается. Возвращаемся к трем. В 17 литровую банку влезет 3 пятилитровых. Записываем результат в форму: 3 пишем под чертой, под делителем. 3 – это неполное частное.
3. Определение остатка. 3*5=15. 15 записываем под делимым. Подводим черту (обозначает знак «=»). Вычитаем из делимого полученное число: 17-15=2. Записываем результат ниже под чертой – в столбик (отсюда и название алгоритма). 2 – это остаток.

Обратите внимание! При делении таким образом, остаток всегда должен быть меньше делителя.

Когда делитель больше делимого

Вызывают затруднение случаи, когда делитель получается больше делимого. Десятичные дроби в программе за 3 класс еще не изучаются, но, следуя логике, ответ надо записывать в виде дроби – в лучшем случае десятичной, в худшем – простой. Но (!) помимо программы, методику вычисления ограничивает поставленная задача: необходимо не разделить, а найти остаток! Дробная часть им не является! Как решить такую задачу?

Обратите внимание! Существует правило для случаев, когда делитель больше делимого: неполное частное равно 0, остаток равен делимому.

Как разделить число 5 на число 6, выделив остаток? Сколько 6-литровых банок влезет в пятилитровую? Ноль, потому что 6 больше 5.

По заданию необходимо заполнить 5 литров – не заполнено ни одного. Значит, остались все 5. Ответ: неполное частное = 0, остаток = 5.

Деление начинают изучать в третьем классе школы. К этому времени ученики уже должны освоить таблицу умножения, что позволяет им совершать деление двузначных чисел на однозначные.

Решите задачу: 18 конфет нужно раздать пятерым детям. Сколько конфет останется?

Примеры:

14:3

Находим неполное частное: 3*1=3, 3*2=6, 3*3=9, 3*4=12, 3*5=15. 5 – перебор. Возвращаемся к 4.

Остаток: 3*4=12, 14-12=2.

Ответ: неполное частное 4, осталось 2.

Вы можете спросить, почему при делении на 2, остаток либо равен 1, либо 0. По таблице умножения, между цифрами, кратными двум существует разница в единицу.

Еще одна задача: 3 пирожка надо разделить на двоих.

4 пирожка разделить на двоих.

5 пирожков разделить на двоих.

Это интересно! Изучение точного предмета: натуральные числа — это какие числа, примеры и свойства

Работа с многозначными числами

Программа за 4 класс предлагает более сложный процесс проведения деления с увеличением расчетных чисел. Если в третьем классе расчеты проводились на основе базовой таблицы умножения в пределах от 1 до 10, то четвероклассники вычисления проводят с многозначными числами более 100.

Данное действие удобнее всего выполнять в столбик, так как неполное частное также будет двузначным числом (в большинстве случаев), а алгоритм столбика облегчает вычисления и делает их более наглядными.

Разделим многозначные числа на двузначные: 386:25

Данный пример отличается от предыдущих количеством уровней расчета, хотя вычисления проводят по тому же принципу, что и ранее. Рассмотрим подробнее:

386 – делимое, 25 – делитель. Необходимо найти неполное частное и выделить остаток.

Первый уровень

Делитель – двузначное число. Делимое – трехзначное. Выделяем у делимого первые две левые цифры – это 38. Сравниваем их с делителем. 38 больше 25? Да, значит, 38 можно разделить на 25. Сколько целых 25 входит в 38?

25*1=25, 25*2=50. 50 больше 38, возвращаемся на один шаг назад.

Ответ – 1. Записываем единицу в зону не полного частного.

Далее:

38-25=13. Записываем число 13 под чертой.

Второй уровень

13 больше 25? Нет – значит можно «опустить» цифру 6 вниз, дописав ее рядом с 13, справа. Получилось 136. 136 больше 25? Да – значит можно его вычесть. Сколько раз 25 поместиться в 136?

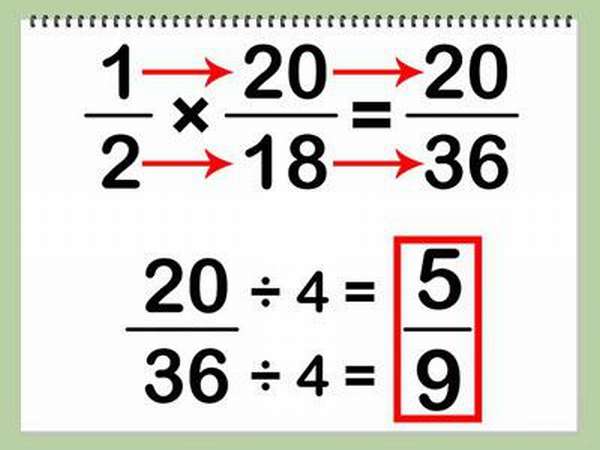
25*1=25, 25*2=50, 25*3=75, 25*4=100, 25*5=125, 256*=150. 150 больше 136 – возвращаемся назад на один шаг. Записываем цифру 5 в зону неполного частного, справа от единицы.

Вычисляем остаток:

136-125=11. Записываем под чертой. 11 больше 25? Нет – деление провести нельзя. У делимого остались цифры? Нет – делить больше нечего. Вычисления закончены.

Ответ: неполное частное равно 15, в остатке 11.

А если будет предложено такое деление, когда двузначный делитель больше первых двух цифр многозначного делимого? В таком случае, третья (четвертая, пятая и последующая) цифра делимого принимает участие в вычислениях сразу.

Приведем примеры на деление с трех- и четырехзначными числами:

386:75

75 – двузначное число. 386 – трехзначное. Сравниваем первые две цифры слева с делителем. 38 больше 75? Нет – деление провести нельзя. Берем все 3 цифры. 386 больше 75? Да – деление провести можно. Проводим вычисления.

75*1=75, 75*2=150, 75*3=225, 75*4=300, 75*5= 375, 75*6=450. 450 больше 386 – возвращаемся на шаг назад. Записываем 5 в зону неполного частного.

Находим остаток: 386-375=11. 11 больше 75? Нет. Еще остались цифры у делимого? Нет. Вычисления закончены.

Ответ: неполное частное = 5, в остатке 11.

119:35

Выполняем проверку: 11 больше 35? Нет – деление провести нельзя. Подставляем третье число – 119 больше 35? Да – действие провести можем.

35*1=35, 35*2=70, 35*3=105, 35*4=140. 140 больше 119 – возвращаемся на один шаг назад. Записываем 3 в зону неполного остатка.

Находим остаток: 119-105=14. 14 больше 35? Нет. Остались цифры у делимого? Нет. Вычисления закончены.

Ответ: неполное частное = 3, осталось 14.

1195:99

Проверяем: 11 больше 99? Нет – подставляем еще одну цифру. 119 больше 99? Да – начинаем вычисления.

11&lt,99, 119&gt,99.

99*1=99, 99*2=198 – перебор. Записываем 1 в неполное частное.

Находим остаток: 119-99=20. 20&lt,99. Опускаем 5. 205&gt,99. Вычисляем.

99*1=99, 99*2=198, 99*3=297. Перебор. Записываем 2 в неполное частное.

Находим остаток: 205-198=7.

Ответ: неполное частное = 12, остаток 7.

Деление с остатком примеры

Учимся делить в столбик с остатком

Вывод

Таким образом проводятся вычисления. Если быть внимательным и выполнять правила, то ничего сложного здесь не будет. Каждый школьник может научиться считать столбиком, потому что это быстро и удобно.

Это интересно! Легкие правила округления чисел после запятой

Разработка урока по
математике в 4 классе

Учитель : Петрова Ирина Анатольевна             

 МБОУ « Школа №20» г. Пласта

Тема
:Деление с остатком

  Цель: развивать
умения выполнять деление с остатком и делать проверку;     совершенствовать
вычислительные навыки, умение решать задачи.

Планируемые результаты: учащиеся
научатся выполнять деление с остатком и делать проверку; моделировать с помощью
схематических чертежей и решать задачи изученных видов; выполнять преобразования
единиц измерения, используя соотношения между ними; работать в парах

I
Орг. момент

    — Сегодняшний урок, я хочу  начать
словами французского философа Жан Жак Руссо : Вы талантливые дети!  Когда — нибудь
, вы сами приятно поразитесь, какие вы умные, как много и хорошо умеете, если
будите постоянно работать над собой, ставить новые цели к их достижению.

   — Я ,  желаю вам сегодня на уроке
убедится в словах Ж.Ж.Руссо.

    — Вы готовы?  Молодцы.

II  Актуализация
знаний.

Запишите число и классная
работа.

1.      Запишите
только ответ.

1ч 10 мин,  ½
часа, ¼ метра, частное чисел 810 и 9 , частное чисел 1000 и 20 , вырази в
метрах 1 км 400м .

70, 30, 25, 90,
50, 1400

-Какое число
лишнее? Почему?

2. Индивидуально у
доски

х- 24= 140:
2                                    х : 6 = 27: 3

-Как найти
неизвестное уменьшаемое?                                                                                                         
— Как найти неизвестное  делимое 
?                                                                                        

3.Работа над задачами

   — Бригада
заасфальтировала 1200 м  за 2 дня. Сколько метров  асфальтирую укладывают
рабочие в 1 день?

 _   Длина участка
20 м , ширина 8м . Чему равна площадь?

 — Площадь участка 270 м ² ,
ширина 3 м .Чему равна длина?

III Актуализация знаний .

-Что общего ?

 -Разделите на группы.

 -Найдите значения выражений.                                                                                                    
       -Назовите компоненты при делении 1 столбика.  ( 2 столбика ) 

— Как выполнить проверку? Чтобы найти
делимое нужно частное умножить на делитель и  прибавить остаток

Как . вы думаете над какой темой мы будем
работать на уроке ? Какие задачи будем ставить перед собой.

IV 
Работа над новой темой

№ 308 ( с.76)

Примеры 1, 2 –устно, пример 3 –
самостоятельно. Самопроверка.

Вывод: Чтобы найти делимое нужно частное
умножить на делитель и прибавить остаток

№ 309 ( 1 коллективно с комментированием,
2 самостоятельно. Индивидуальная доска)

Повторим название компонентов при делении

Вывод: Чтобы найти делимое нужно частное
умножить на делитель и прибавить остаток

V
Физ. минутка для глаз

VI
Закрепление изученного.

№ 311 (у доски с объяснением)

1км-1000м

1)      15000
: 30 = 500 (м)  — за 1 день 1 бригада

2)      1500
: 60 = 250( м) – за 1 день 2 бригада

3)      500
+250 =750 ( м) – обе бригады за 1 день

4)      1500
: 750 = 20 ( д)  — обе бригады , работая вместе.

Ответ : за 20 дней
.

№ 310

— Прочитайте
задачу.                                                                                                                                
– Как найти ширину, зная  площадь и длину?                                           
                                            – Как найти длину, зная  площадь и
ширину?                                                                                    
— Сделайте чертёж и решите задачу самостоятельно

1) 150 * 80 = 12000 (м ²) –
площадь 2 участка

2) 12000 : 60 = 200 ( м)  — длина 1
участка.

 Ответ : 200 м.

№ 314  (по рядам и у доски)

Вывод: Чтобы найти делимое нужно частное
умножить на делитель и прибавить остаток

№ 313 ( 1 строчку у доски)

VI
Подведение итогов

— Какие вычислительные приёмы мы повторяли
на уроке?  

— Как проверить деление с остатком?

Рефлексия

Закончите мои фразы

Сегодня на уроке я  научился……

Самым интересным заданием было….

Порадовался тому, что …..

Оценки за работу на уроке.

VI 
Д.з 

№ 312,  313 ( 2 строчка) ( с.76)