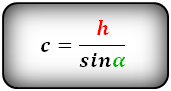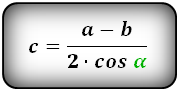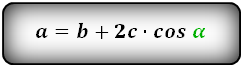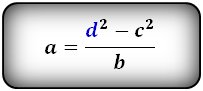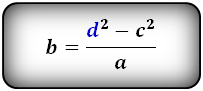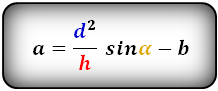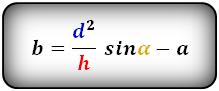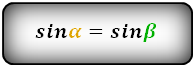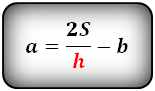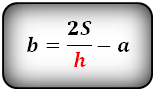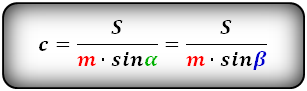1. Формула длины основания равнобедренной трапеции через среднюю линию
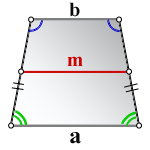
a — нижнее основание
b — верхнее основание
m — средняя линия
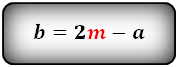
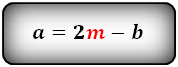
Формулы длины основания:
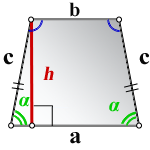
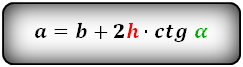
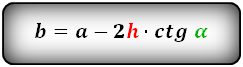
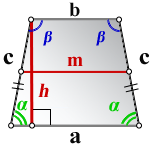
2. Формулы длины сторон через высоту и угол при нижнем основании
a — нижнее основание
b — верхнее основание
c — равные боковые стороны
α — угол при основании трапеции
h — высота трапеции
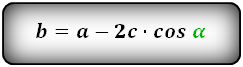
Формулы всех четырех сторон трапеции:
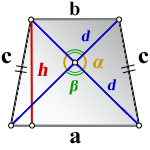
3. Формула длины сторон трапеции через диагонали, высоту и угол между диагоналями
a — нижнее основание
b — верхнее основание
c — равные боковые стороны
d — диагонали
α , β — углы между диагоналями
h — высота трапеции
Формулы длины сторон трапеции:
справедливо для данной ситуации:
4. Формулы длины сторон равнобедренной трапеции через площадь
a — нижнее основание
b — верхнее основание
c — равные боковые стороны
α , β — углы при основаниях
m — средняя линия
h — средняя линия
Формулы длины сторон равнобедренной трапеции через площадь:
Формулы площади произвольной трапеции
Формулы площади равнобедренной трапеции
Формула периметра трапеции
Все формулы по геометрии
- Подробности
-
Опубликовано: 08 октября 2013
-
Обновлено: 13 августа 2021
Для начала найдем длины боковых сторон равнобедренной трапеции. Равнобедренная трапеция имеет две параллельные стороны (основания) и две равные не параллельные стороны (боковые стороны). Зная основания и периметр трапеции, мы можем найти длину каждой из боковых сторон.
Основания равны 8 и 18, а периметр равен 52. Обозначим длины боковых сторон трапеции как a и b.
Так как это равнобедренная трапеция, a = b.
Теперь найдем длины боковых сторон:
a + b + 8 + 18 = 52
a + a + 26 = 52
2a = 26
a = 13
Теперь, когда у нас есть длины боковых сторон, давайте найдем высоту трапеции. Высота трапеции опускается перпендикулярно к основаниям. Разделите трапецию на два равнобедренных треугольника. В таком случае, можно использовать теорему Пифагора для одного из этих треугольников.
Разность оснований равна 18 — 8 = 10. Таким образом, каждый из равнобедренных треугольников имеет основание, равное 10/2 = 5.
Теперь используем теорему Пифагора:
a^2 = h^2 + b^2
13^2 = h^2 + 5^2
169 = h^2 + 25
h^2 = 144
h = 12
Теперь, когда у нас есть высота и основания трапеции, мы можем найти её площадь. Формула для площади трапеции:
S = ((a + b) / 2) * h
S = ((8 + 18) / 2) * 12
S = (26 / 2) * 12
S = 13 * 12
S = 156
Площадь равнобедренной трапеции равна 156 квадратных единиц.
В равнобокой трапеции боковые стороны и углы при основаниях равны между собой, следовательно, все формулы значительно упрощаются. Периметр такой трапеции равен сумме двух оснований и удвоенной боковой стороны.
P=2a+b+d
Высота равнобокой трапеции является катетом в прямоугольном треугольнике, где гипотенуза – боковая сторона трапеции, а второй катет – половина разности большего и меньшего оснований. Вычислить высоту в равнобокой трапеции можно с помощью теоремы Пифагора в этом треугольнике. (рис.104.1)
h=√(a^2-(c-b)^2/4)
Средняя линия трапеции не связана с боковыми сторонами и представляет собой сумму большего и меньшего основании, разделенную на два.
m=(b+c)/2
Площадь равнобокой трапеции вычисляется также как и обычной – произведением высоты на среднюю линию.
S=hm
Найти диагонали в равнобокой трапеции проще, так как высоты, входящие с ними в прямоугольные треугольники, делят большее основание на три части, одна из которых равна меньшему основанию, а две другие равны между собой. Сами диагонали также равны друг другу и вычислить их можно по формулам, приведенным из теоремы Пифагора. (рис.104.2)
d=√(h^2+((b+c)/2)^2 )=√(a^2-(c-b)^2/4+(b+c)^2/4)=√((2a^2-b^2-c^2)/2)
Внутри равнобокой окружности можно вписать окружность, радиус которой будет равен квадратному корню из произведения оснований, деленному на два, если сумма боковых сторон равна сумме оснований (что представляет собой половину высоты) (рис.104.3)
r=√bc/2
Радиус окружности, описанной вокруг равнобокой трапеции, ищется как радиус описанной окружности треугольника, образованного ее диагональю со сторонами. (рис.104.4)
R=abd/√((a+b+d)(a+b)(a+d)(b+d))
В данной публикации мы рассмотрим, каким образом можно посчитать периметр трапеции и разберем примеры решения задач.
- Формула вычисления периметра
- Примеры задач
Формула вычисления периметра
Периметр (P) трапеции равняется сумме длин всех ее сторон.
P = a + b + c + d
- b и d – основания трапеции;
- a и с – ее боковые стороны.
Периметр равнобедренной трапеции
В равнобедренной трапеции боковые стороны равны (a=c), из-за чего ее, также, называют равнобокой. Периметр считается так:
P = 2a + b + d или P = 2с + b + d
Периметр прямоугольной трапеции
Для расчета периметра используется такая же формула, что и для разносторонней трапеции.
P = a + b + c + d
Примеры задач
Задание 1
Найдите периметр трапеции, если ее основания равны 7 и 10 см, а боковые стороны – 4 и 5 см.
Решение:
Используем стандартную формулу, подставив в нее известные нам длины сторон: P = 7 см + 10 см + 4 см + 5 см = 26 см.
Задание 2
Периметр равнобедренной трапеции равняется 22 см. Найдите длину боковой стороны, если основания фигуры равны 3 см и 9 см.
Решение:
Как мы знаем, периметр равнобедренной трапеции вычисляется по формуле: P = 2a + b + d, где а – боковая сторона.
Ее длина, умноженная на два равна: 2a = P – b – d = 22 см – 3 см – 9 см = 10 см.
Следовательно, длина боковой стороны составляет: a = 10 см / 2 = 5 см.
Как найти основания трапеции
Основания трапеции можно найти несколькими способами, в зависимости от заданных параметров. При известной площади, высоте и боковой стороне равнобокой трапеции последовательность расчетов сводится к вычислениям стороны равнобедренного треугольника. А также к использованию свойства равнобокой трапеции.

Инструкция
Начертите равнобокую трапецию. Дана площадь трапеции — S, высота трапеции — h и боковая сторона — a. Опустите высоту трапеции на большее основание. Большее основание будет разделено на отрезки m и n.

Для определения длины обоих оснований (х, y) примените свойство равнобокой трапеции и формулу расчета площади трапеции.
Согласно свойству равнобокой трапеции отрезок n равен полуразности оснований х и y. Следовательно, меньшее основание трапеции y можно представить в виде разности большего основания и отрезка n, помноженного на два: y = x — 2*n.
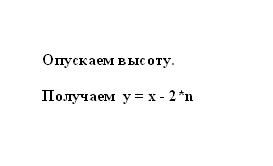
Найдите неизвестный меньший отрезок n. Для этого вычислите одну их сторон получившегося прямоугольного треугольника. Треугольник образован высотой – h (катет), боковой стороной – a (гипотенуза) и отрезком – n (катет). Согласно теореме Пифагора неизвестный катет n² = a² — h². Подставьте известные числовые значения и высчитайте квадрат катета n. Возьмите корень квадратный из полученного значения – это и будет длина отрезка n.
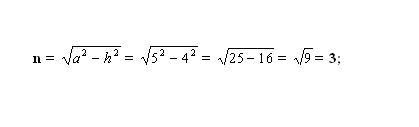
Подставьте полученное значение в первое уравнение для вычисления y. Площадь трапеции высчитывается по формуле S = ((х + y)*h)/2. Выразите неизвестную переменную: y = 2*S/h – х.
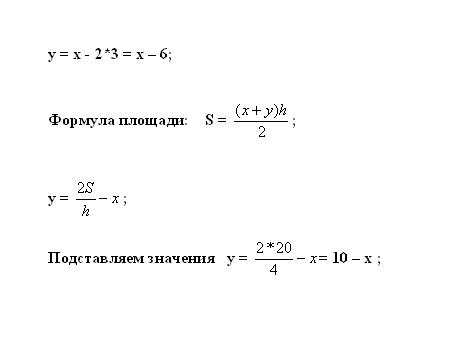
Запишите оба полученных уравнения в систему. Подставляя известные значения, найдите две искомые величины в системе двух уравнений. Полученное решение системы х представляет собой длину большего основания, а y — меньшего основания.

Источники:
- высота равнобокой трапеции