Для того чтобы определить какая допущена здесь ошибка, необходимо, рассмотреть данный набор цифр с двух сторон:
Первое, допускаем что этот набор цифр обычное число, тогда здесь все правильно, число 123456789 как не верти останется числом.
Второе если подойти к данному набору цифр с точки зрения перечня Арабских цифр, то конечно здесь отсутствует цифра 0 (ноль) и тогда правильно будет следующая последовательность Арабских цифр; 0123456789.
Просто, другое что то искать в правописании предложения я не стал рассматривать, думая именно что речь здесь об Арабских цифрах, Если это вопрос на засыпку?
Повторяется также слово найти.
Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel 2021 Excel 2021 для Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel 2007 Excel для Mac 2011 Excel Starter 2010 Еще…Меньше
Кроме неожиданных результатов, формулы иногда возвращают значения ошибок. Ниже представлены некоторые инструменты, с помощью которых вы можете искать и исследовать причины этих ошибок и определять решения.
Примечание: В статье также приводятся методы, которые помогут вам исправлять ошибки в формулах. Этот список не исчерпывающий — он не охватывает все возможные ошибки формул. Для получения справки по конкретным ошибкам поищите ответ на свой вопрос или задайте его на форуме сообщества Microsoft Excel.
Ввод простой формулы
Формулы — это выражения, с помощью которых выполняются вычисления со значениями на листе. Формула начинается со знака равенства (=). Например, следующая формула складывает числа 3 и 1:
=3+1
Формула также может содержать один или несколько из таких элементов: функции, ссылки, операторы и константы.
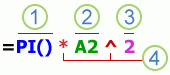
Части формулы
-
Функции: это специальные формулы Excel, которые выполняют определенные вычисления. Например, функция ПИ() возвращает значение числа Пи: 3,142…
-
Ссылки: это ссылки на отдельные ячейки или диапазоны. Например, A2 возвращает значение ячейки A2.
-
Константы. Числа или текстовые значения, введенные непосредственно в формулу, например 2.
-
Операторы: оператор * (звездочка) служит для умножения чисел, а оператор ^ (крышка) — для возведения числа в степень. С помощью + и – можно складывать и вычитать значения, а с помощью / — делить их.
Примечание: Для некоторых функций требуются так называемые аргументы. Аргументы — это значения, которые некоторые функции используют при вычислениях. Аргументы функции указываются в ее скобках (). Функция ПИ не требует аргументов, поэтому у нее пустые скобки. У некоторых функций несколько аргументов, в том числе необязательные. Аргументы разделяются точкой с запятой (;).
Например, функция СУММ требует только один аргумент, но у нее может быть до 255 аргументов (включительно).
Пример одного аргумента: =СУММ(A1:A10).
Пример нескольких аргументов: =СУММ(A1:A10;C1:C10).
В приведенной ниже таблице собраны некоторые наиболее частые ошибки, которые допускают пользователи при вводе формулы, и описаны способы их исправления.
|
Рекомендация |
Дополнительные сведения |
|
Начинайте каждую формулу со знака равенства (=) |
Если опустить знак равенства, введенные данные могут отображаться в виде текста или даты. Например, при вводе СУММ(A1:A10)Excel отображает текстовую строку SUM(A1:A10) и не выполняет вычисление. Если ввести значение 11/2, вместо деления 11 на 2 Excel отображается дата 2–ноя (при условии, что ячейка имеет формат «Общий«) вместо деления 11 на 2. |
|
Следите за соответствием открывающих и закрывающих скобок |
Все скобки должны быть парными (открывающая и закрывающая). Если в формуле используется функция, для ее правильной работы важно, чтобы все скобки стояли в правильных местах. Например, формула =ЕСЛИ(B5<0);»Недопустимо»;B5*1,05) не будет работать, поскольку в ней две закрывающие скобки и только одна открывающая (требуется одна открывающая и одна закрывающая). Правильный вариант этой формулы выглядит так: =ЕСЛИ(B5<0;»Недопустимо»;B5*1,05). |
|
Для указания диапазона используйте двоеточие |
Указывая диапазон ячеек, разделяйте с помощью двоеточия (:) ссылку на первую ячейку в диапазоне и ссылку на последнюю ячейку в диапазоне. Например, =SUM(A1:A5), а не =SUM(A1 A5), которые возвращают #NULL! Ошибка. |
|
Вводите все обязательные аргументы |
У некоторых функций есть обязательные аргументы. Старайтесь также не вводить слишком много аргументов. |
|
Вводите аргументы правильного типа |
В некоторых функциях, например СУММ, необходимо использовать числовые аргументы. В других функциях, например ЗАМЕНИТЬ, требуется, чтобы хотя бы один аргумент имел текстовое значение. Если использовать в качестве аргумента данные неправильного типа, Excel может возвращать непредвиденные результаты или ошибку. |
|
Число уровней вложения функций не должно превышать 64 |
В функцию можно вводить (или вкладывать) не более 64 уровней вложенных функций. |
|
Имена других листов должны быть заключены в одинарные кавычки |
Если формула содержит ссылки на значения или ячейки на других листах или в других книгах, а имя другой книги или листа содержит пробелы или другие небуквенные символы, его необходимо заключить в одиночные кавычки (‘), например: =’Данные за квартал’!D3 или =‘123’!A1. |
|
Указывайте после имени листа восклицательный знак (!), когда ссылаетесь на него в формуле |
Например, чтобы возвратить значение ячейки D3 листа «Данные за квартал» в той же книге, воспользуйтесь формулой =’Данные за квартал’!D3. |
|
Указывайте путь к внешним книгам |
Убедитесь, что каждая внешняя ссылка содержит имя книги и путь к ней. Ссылка на книгу содержит имя книги и должна быть заключена в квадратные скобки ([Имякниги.xlsx]). В ссылке также должно быть указано имя листа в книге. В формулу также можно включить ссылку на книгу, не открытую в Excel. Для этого необходимо указать полный путь к соответствующему файлу, например: =ЧСТРОК(‘C:My Documents[Показатели за 2-й квартал.xlsx]Продажи’!A1:A8). Эта формула возвращает количество строк в диапазоне ячеек с A1 по A8 в другой книге (8). Примечание: Если полный путь содержит пробелы, как в приведенном выше примере, необходимо заключить его в одиночные кавычки (в начале пути и после имени книги перед восклицательным знаком). |
|
Числа нужно вводить без форматирования |
Не форматируйте числа, которые вводите в формулу. Например, если нужно ввести в формулу значение 1 000 рублей, введите 1000. Если вы введете какой-нибудь символ в числе, Excel будет считать его разделителем. Если вам нужно, чтобы числа отображались с разделителями тысяч или символами валюты, отформатируйте ячейки после ввода чисел. Например, если для прибавления 3100 к значению в ячейке A3 используется формула =СУММ(3 100;A3), Excel не складывает 3100 и значение в ячейке A3 (как было бы при использовании формулы =СУММ(3100;A3)), а суммирует числа 3 и 100, после чего прибавляет полученный результат к значению в ячейке A3. Другой пример: если ввести =ABS(-2 134), Excel выведет ошибку, так как функция ABS принимает только один аргумент: =ABS(-2134). |
Вы можете использовать определенные правила для поиска ошибок в формулах. Они не гарантируют исправление всех ошибок на листе, но могут помочь избежать распространенных проблем. Эти правила можно включать и отключать независимо друг от друга.
Существуют два способа пометки и исправления ошибок: последовательно (как при проверке орфографии) или сразу при появлении ошибки во время ввода данных на листе.
Ошибку можно исправить с помощью параметров, отображаемых приложением Excel, или игнорировать, щелкнув команду Пропустить ошибку. Ошибка, пропущенная в конкретной ячейке, не будет больше появляться в этой ячейке при последующих проверках. Однако все пропущенные ранее ошибки можно сбросить, чтобы они снова появились.
-
Для Excel в Windows щелкните Параметры > файла > формулы.
Для Excel на Mac щелкните меню Excel > Параметры > проверки ошибок.В Excel 2007 нажмите кнопку Microsoft Office
и выберите Параметры Excel > Формулы.
-
В разделе Поиск ошибок установите флажок Включить фоновый поиск ошибок. Все найденные ошибки помечаются треугольником в левом верхнем углу ячейки.
-
Чтобы изменить цвет треугольника, которым помечаются ошибки, выберите нужный цвет в поле Цвет индикаторов ошибок.
-
В разделе Правила поиска ошибок установите или снимите флажок для любого из следующих правил:
-
Ячейки, содержащие формулы, которые приводят к ошибке. Формула не использует ожидаемый синтаксис, аргументы или типы данных. Значения ошибок: #DIV/0!, #N/A, #NAME?, #NULL!, #NUM!, #REF!и #VALUE!. Каждое из этих значений ошибок имеет разные причины и разрешается по-разному.
Примечание: Если ввести значение ошибки прямо в ячейку, оно сохраняется как значение ошибки, но не помечается как ошибка. Но если на эту ячейку ссылается формула из другой ячейки, эта формула возвращает значение ошибки из ячейки.
-
Несогласованная формула вычисляемого столбца в таблицах. Вычисляемый столбец может содержать отдельные формулы, отличающиеся от формулы столбца master, что создает исключение. Исключения вычисляемого столбца возникают при указанных ниже действиях.
-
Ввод данных, не являющихся формулой, в ячейку вычисляемого столбца.
-
Введите формулу в ячейку вычисляемого столбца, а затем нажмите клавиши CTRL+Z или нажмите кнопку Отменить
на панели быстрого доступа.
-
Ввод новой формулы в вычисляемый столбец, который уже содержит одно или несколько исключений.
-
Копирование в вычисляемый столбец данных, не соответствующих формуле столбца. Если копируемые данные содержат формулу, эта формула перезапишет данные в вычисляемом столбце.
-
Перемещение или удаление ячейки из другой области листа, если на эту ячейку ссылалась одна из строк в вычисляемом столбце.
-
-
Ячейки, содержащие годы, представленные в виде 2 цифр: ячейка содержит текстовую дату, которая может быть неправильно интерпретирована как неправильный век, если она используется в формулах. Например, дата в формуле =ГОД(«1.1.31») может относиться как к 1931, так и к 2031 году. Используйте это правило для выявления дат в текстовом формате, допускающих двоякое толкование.
-
Числа в формате текста или предшествуют апострофу. Ячейка содержит числа, хранящиеся в виде текста. Обычно это является следствием импорта данных из других источников. Числа, хранящиеся как текст, могут стать причиной неправильной сортировки, поэтому лучше преобразовать их в числовой формат. ‘=SUM(A1:A10) рассматривается как текст.
-
Формулы, несовместимые с другими формулами в регионе. Формула не соответствует шаблону других формул, расположенных рядом с ней. Во многих случаях формулы, соседствующие с другими формулами, отличаются только используемыми ссылками. В следующем примере из четырех смежных формул Excel отображает ошибку рядом с формулой =СУММ(A10:C10) в ячейке D4, так как смежные формулы увеличиваются на одну строку, а одна — на 8 строк. Excel ожидает формулу =СУММ(A4:C4).
Если используемые в формуле ссылки не соответствуют ссылкам в смежных формулах, приложение Microsoft Excel сообщит об ошибке.
-
Формулы, опускающие ячейки в области. Формула не может автоматически включать ссылки на данные, которые вы вставляете между исходным диапазоном данных и ячейкой, содержащей формулу. Это правило позволяет сравнить ссылку в формуле с фактическим диапазоном ячеек, смежных с ячейкой, содержащей формулу. Если смежные ячейки содержат дополнительные значения и не являются пустыми, Excel отображает рядом с формулой ошибку.
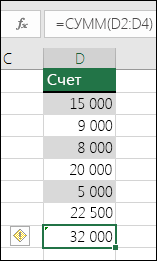
Например, при использовании этого правила Excel отображает ошибку для формулы =СУММ(D2:D4), поскольку ячейки D5, D6 и D7, смежные с ячейками, на которые ссылается формула, и ячейкой с формулой (D8), содержат данные, на которые должна ссылаться формула.
-
Незаблокированные ячейки, содержащие формулы. Формула не заблокирована для защиты. По умолчанию все ячейки на листе блокируются, поэтому их нельзя изменить при защите листа. Это поможет избежать случайных ошибок, таких как случайное удаление или изменение формул. Эта ошибка указывает, что ячейка была разблокирована, но лист не был защищен. Убедитесь, что ячейка не заблокирована.
-
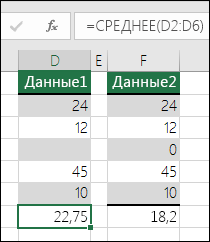
Формулы, ссылающиеся на пустые ячейки. Формула содержит ссылку на пустую ячейку. Это может привести к неверным результатам, как показано в приведенном далее примере.
Предположим, требуется найти среднее значение чисел в приведенном ниже столбце ячеек. Если третья ячейка пуста, она не используется в расчете, поэтому результатом будет значение 22,75. Если эта ячейка содержит значение 0, результат будет равен 18,2.
-
Данные, введенные в таблицу, недопустимы. В таблице возникает ошибка проверки. Проверьте параметр проверки ячейки, перейдя на вкладку Данные > группу Data Tools > Проверка данных.
-
-
Выберите лист, на котором требуется проверить наличие ошибок.
-
Если расчет листа выполнен вручную, нажмите клавишу F9, чтобы выполнить расчет повторно.
Если диалоговое окно Поиск ошибок не отображается, щелкните вкладку Формулы, выберите Зависимости формул и нажмите кнопку Поиск ошибок.
-
Чтобы повторно проверить пропущенные ранее ошибки, щелкните Файл > Параметры > Формулы. Для Excel на Mac щелкните меню Excel > Параметры > проверки ошибок.
В разделе Поиск ошибок выберите Сброс пропущенных ошибок и нажмите кнопку ОК.
Примечание: Сброс пропущенных ошибок применяется ко всем ошибкам, которые были пропущены на всех листах активной книги.
Совет: Советуем расположить диалоговое окно Поиск ошибок непосредственно под строкой формул.
-
Нажмите одну из управляющих кнопок в правой части диалогового окна. Доступные действия зависят от типа ошибки.
-
Нажмите кнопку Далее.
Примечание: Если нажать кнопку Пропустить ошибку, помеченная ошибка при последующих проверках будет пропускаться.
-
Рядом с ячейкой нажмите кнопку «Проверка ошибок »
, а затем выберите нужный параметр. Доступные команды различаются для каждого типа ошибки, и первая запись описывает ошибку.
Если нажать кнопку Пропустить ошибку, помеченная ошибка при последующих проверках будет пропускаться.
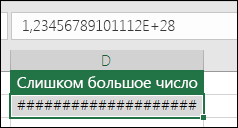
Если формула не может правильно вычислить результат, в Excel отображается значение ошибки, например #####, #ДЕЛ/0!, #Н/Д, #ИМЯ?, #ПУСТО!, #ЧИСЛО!, #ССЫЛКА!, #ЗНАЧ!. Ошибки разного типа имеют разные причины и разные способы решения.
Приведенная ниже таблица содержит ссылки на статьи, в которых подробно описаны эти ошибки, и краткое описание.
|
Статья |
Описание |
|
Исправление ошибки #### |
Эта ошибка отображается в Excel, если столбец недостаточно широк, чтобы показать все символы в ячейке, или ячейка содержит отрицательное значение даты или времени. Например, результатом формулы, вычитающей дату в будущем из даты в прошлом (=15.06.2008-01.07.2008), является отрицательное значение даты. Совет: Попробуйте автоматически изменить ширину ячейки, дважды щелкнув между заголовками столбцов. Если ### отображается потому, что Excel не может отобразить все знаки, эта проблема будет исправлена. |
|
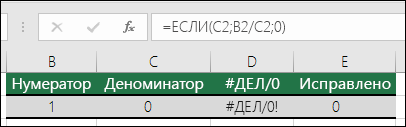
Исправление ошибки #ДЕЛ/0! ошибка |
Эта ошибка отображается в Excel, если число делится на ноль (0) или на ячейку без значения. Совет: Добавьте обработчик ошибок, как в примере ниже: =ЕСЛИ(C2;B2/C2;0). |
|
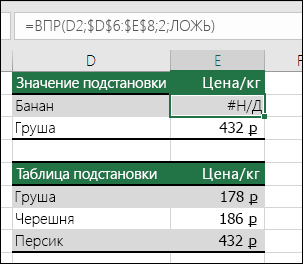
Исправление ошибки #Н/Д |
Эта ошибка отображается в Excel, если функции или формуле недоступно значение. Если вы используете такую функцию, как ВПР, есть ли для искомого значения соответствие в диапазоне поиска? Скорее всего, нет. Используйте функцию ЕСЛИОШИБКА для подавления ошибки #Н/Д. В этом случае можно ввести следующее: =ЕСЛИОШИБКА(ВПР(D2;$D$6:$E$8;2;ИСТИНА);0) |
|
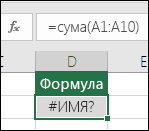
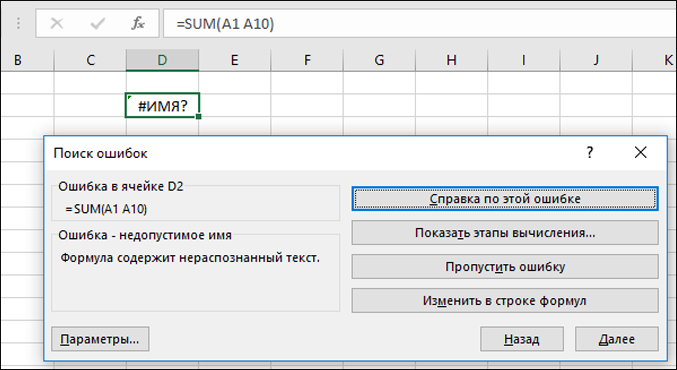
Исправление ошибки #ИМЯ? ошибка |
Эта ошибка отображается, если Excel не распознает текст в формуле. Например имя диапазона или имя функции написано неправильно. Примечание: Если вы используете функцию, убедитесь, что ее имя написано неправильно. В данном случае слово СУММ введено с ошибкой. Удалите «а», и Excel исправит формулу. |
|
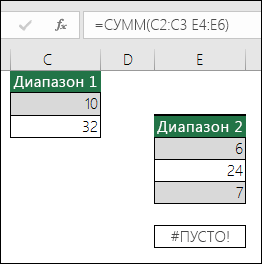
Исправление ошибки #ПУСТО! |
Эта ошибка отображается в Excel, когда вы указываете пересечение двух областей, которые не пересекаются. Оператором пересечения является пробел, разделяющий ссылки в формуле. Примечание: Убедитесь, что диапазоны разделены правильно: области C2:C3 и E4:E6 не пересекаются, поэтому ввод формулы =СУММ(C2:C3 E4:E6) возвращает #NULL! могут вызвать текст и специальные знаки в ячейке. Если поставить запятую между диапазонами C и E, она будет исправлена =СУММ(C2:C3;E4:E6) |
|
Исправление ошибки #ЧИСЛО! ошибка |
Эта ошибка отображается в Excel, если формула или функция содержит недопустимые числовые значения. Используете ли вы функцию, которая выполняет итерацию, например IRR или RATE? Если да, то #NUM! ошибка, вероятно, из-за того, что функция не может найти результат. Инструкции по устранению неполадок см. в разделе справки. |
|
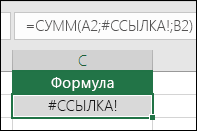
Исправление ошибки #ССЫЛКА! ошибка |
Эта ошибка отображается в Excel при наличии недопустимой ссылки на ячейку. Например, вы удалили ячейки, на которые ссылались другие формулы, или вставили поверх них другие ячейки. Вы случайно удалили строку или столбец? Смотрите, что произошло после удаления столбца B в формуле =СУММ(A2;B2;C2). Нажмите кнопку Отменить (или клавиши CTRL+Z), чтобы отменить удаление, измените формулу или используйте ссылку на непрерывный диапазон (=СУММ(A2:C2)), которая автоматически обновится при удалении столбца B. |
|
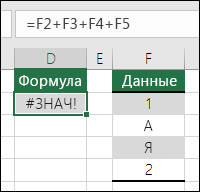
Исправление ошибки #ЗНАЧ! ошибка |
Эта ошибка отображается в Excel, если в формуле используются ячейки, содержащие данные не того типа. Вы используйте математические операторы (+, -, *, / ^) с разными типами данных? В таком случае попробуйте использовать вместо них функцию. В этом случае =СУММ(F2:F5) поможет устранить проблему. |
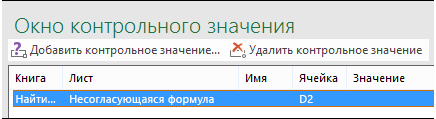
Если ячейки не видны на листе, для просмотра их и содержащихся в них формул можно использовать панель инструментов «Окно контрольного значения». С помощью окна контрольного значения удобно изучать, проверять зависимости или подтверждать вычисления и результаты формул на больших листах. При этом вам не требуется многократно прокручивать экран или переходить к разным частям листа.
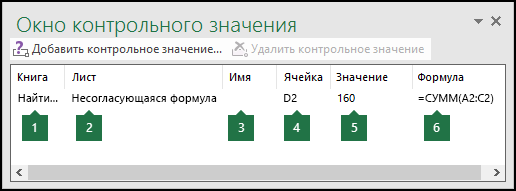
Эту панель инструментов можно перемещать и закреплять, как и любую другую. Например, можно закрепить ее в нижней части окна. На панели инструментов выводятся следующие свойства ячейки: 1) книга, 2) лист, 3) имя (если ячейка входит в именованный диапазон), 4) адрес ячейки 5) значение и 6) формула.
Примечание: Для каждой ячейки может быть только одно контрольное значение.
Добавление ячеек в окно контрольного значения
-
Выделите ячейки, которые хотите просмотреть.
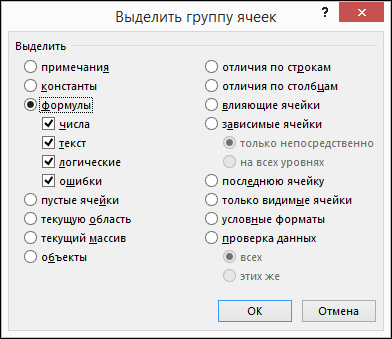
Чтобы выделить все ячейки с формулами, на вкладке Главная в группе Редактирование нажмите кнопку Найти и выделить (вы также можете нажать клавиши CTRL+G или CONTROL+G на компьютере Mac). Затем выберите Выделить группу ячеек и Формулы.
-
На вкладке Формулы в группе Зависимости формул нажмите кнопку Окно контрольного значения.
-
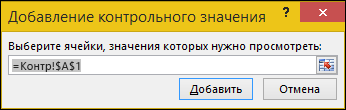
Нажмите кнопку Добавить контрольное значение.
-
Убедитесь, что вы выделили все ячейки, которые хотите отследить, и нажмите кнопку Добавить.
-
Чтобы изменить ширину столбца, перетащите правую границу его заголовка.
-
Чтобы открыть ячейку, ссылка на которую содержится в записи панели инструментов «Окно контрольного значения», дважды щелкните запись.
Примечание: Ячейки, содержащие внешние ссылки на другие книги, отображаются на панели инструментов «Окно контрольного значения» только в случае, если эти книги открыты.
Удаление ячеек из окна контрольного значения
-
Если окно контрольного значения не отображается, на вкладке Формула в группе Зависимости формул нажмите кнопку Окно контрольного значения.
-
Выделите ячейки, которые нужно удалить.
Чтобы выделить несколько ячеек, щелкните их, удерживая нажатой клавишу CTRL.
-
Нажмите кнопку Удалить контрольное значение.
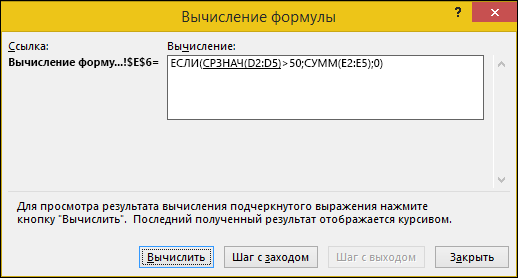
Иногда трудно понять, как вложенная формула вычисляет конечный результат, поскольку в ней выполняется несколько промежуточных вычислений и логических проверок. Но с помощью диалогового окна Вычисление формулы вы можете увидеть, как разные части вложенной формулы вычисляются в заданном порядке. Например, формулу =ЕСЛИ(СРЗНАЧ(D2:D5)>50;СУММ(E2:E5);0) будет легче понять, если вы увидите промежуточные результаты:
|
В диалоговом окне «Вычисление формулы» |
Описание |
|
=ЕСЛИ(СРЗНАЧ(D2:D5)>50;СУММ(E2:E5);0) |
Сначала выводится вложенная формула. Функции СРЗНАЧ и СУММ вложены в функцию ЕСЛИ. Диапазон ячеек D2:D5 содержит значения 55, 35, 45 и 25, поэтому функция СРЗНАЧ(D2:D5) возвращает результат 40. |
|
=ЕСЛИ(40>50;СУММ(E2:E5);0) |
Диапазон ячеек D2:D5 содержит значения 55, 35, 45 и 25, поэтому функция СРЗНАЧ(D2:D5) возвращает результат 40. |
|
=ЕСЛИ(ЛОЖЬ;СУММ(E2:E5);0) |
Поскольку 40 не больше 50, выражение в первом аргументе функции ЕСЛИ (аргумент лог_выражение) имеет значение ЛОЖЬ. Функция ЕСЛИ возвращает значение третьего аргумента (аргумент значение_если_ложь). Функция СУММ не вычисляется, поскольку она является вторым аргументом функции ЕСЛИ (аргумент значение_если_истина) и возвращается только тогда, когда выражение имеет значение ИСТИНА. |
-
Выделите ячейку, которую нужно вычислить. За один раз можно вычислить только одну ячейку.
-
Откройте вкладку Формулы и выберите Зависимости формул > Вычислить формулу.
-
Нажмите кнопку Вычислить, чтобы проверить значение подчеркнутой ссылки. Результат вычисления отображается курсивом.
Если подчеркнутая часть формулы является ссылкой на другую формулу, нажмите кнопку Шаг с заходом, чтобы отобразить другую формулу в поле Вычисление. Нажмите кнопку Шаг с выходом, чтобы вернуться к предыдущей ячейке и формуле.
Кнопка Шаг с заходом недоступна для ссылки, если ссылка используется в формуле во второй раз или если формула ссылается на ячейку в отдельной книге.
-
Продолжайте нажимать кнопку Вычислить, пока не будут вычислены все части формулы.
-
Чтобы посмотреть вычисление еще раз, нажмите кнопку Начать сначала.
-
Чтобы закончить вычисление, нажмите кнопку Закрыть.
Примечания:
-
Некоторые части формул, в которых используются функции ЕСЛИ и ВЫБОР, не вычисляются. В таких случаях в поле Вычисление отображается значение #Н/Д.
-
Если ссылка пуста, в поле Вычисление отображается нулевое значение (0).
-
Некоторые функции вычисляются заново при каждом изменении листа, так что результаты в диалоговом окне Вычисление формулы могут отличаться от тех, которые отображаются в ячейке. Это функции СЛЧИС, ОБЛАСТИ, ИНДЕКС, СМЕЩ, ЯЧЕЙКА, ДВССЫЛ, ЧСТРОК, ЧИСЛСТОЛБ, ТДАТА, СЕГОДНЯ, СЛУЧМЕЖДУ.
Дополнительные сведения

Вы всегда можете задать вопрос специалисту Excel Tech Community или попросить помощи в сообществе Answers community.
См. также
Отображение связей между формулами и ячейками
Рекомендации, позволяющие избежать появления неработающих формул
Нужна дополнительная помощь?
Нужны дополнительные параметры?
Изучите преимущества подписки, просмотрите учебные курсы, узнайте, как защитить свое устройство и т. д.
В сообществах можно задавать вопросы и отвечать на них, отправлять отзывы и консультироваться с экспертами разных профилей.
Абсолютная и относительная погрешность

4.2
Средняя оценка: 4.2
Всего получено оценок: 2187.
4.2
Средняя оценка: 4.2
Всего получено оценок: 2187.
Абсолютную и относительную погрешность используют для оценки неточности в производимых расчетах с высокой сложностью. Также они используются в различных измерениях и для округления результатов вычислений. Рассмотрим, как определить абсолютную и относительную погрешность.
Опыт работы учителем математики — более 33 лет.
Абсолютная погрешность
Абсолютной погрешностью числа называют разницу между этим числом и его точным значением.
Рассмотрим пример: в школе учится 374 ученика. Если округлить это число до 400, то абсолютная погрешность измерения равна 400-374=26.
Для подсчета абсолютной погрешности необходимо из большего числа вычитать меньшее.
Существует формула абсолютной погрешности. Обозначим точное число буквой А, а буквой а – приближение к точному числу. Приближенное число – это число, которое незначительно отличается от точного и обычно заменяет его в вычислениях. Тогда формула будет выглядеть следующим образом:
Δа=А-а. Как найти абсолютную погрешность по формуле, мы рассмотрели выше.
На практике абсолютной погрешности недостаточно для точной оценки измерения. Редко когда можно точно знать значение измеряемой величины, чтобы рассчитать абсолютную погрешность. Измеряя книгу в 20 см длиной и допустив погрешность в 1 см, можно считать измерение с большой ошибкой. Но если погрешность в 1 см была допущена при измерении стены в 20 метров, это измерение можно считать максимально точным. Поэтому в практике более важное значение имеет определение относительной погрешности измерения.
Записывают абсолютную погрешность числа, используя знак ±. Например, длина рулона обоев составляет 30 м ± 3 см. Границу абсолютной погрешности называют предельной абсолютной погрешностью.
Относительная погрешность
Относительной погрешностью называют отношение абсолютной погрешности числа к самому этому числу. Чтобы рассчитать относительную погрешность в примере с учениками, разделим 26 на 374.
Получим число 0,0695, переведем в проценты и получим 7 %. Относительную погрешность обозначают процентами, потому что это безразмерная величина. Относительная погрешность – это точная оценка ошибки измерений. Если взять абсолютную погрешность в 1 см при измерении длины отрезков 10 см и 10 м, то относительные погрешности будут соответственно равны 10 % и 0,1 %. Для отрезка длиной в 10 см погрешность в 1 см очень велика, это ошибка в 10 %. А для десятиметрового отрезка 1 см не имеет значения, всего 0,1 %.
Различают систематические и случайные погрешности. Систематической называют ту погрешность, которая остается неизменной при повторных измерениях. Случайная погрешность возникает в результате воздействия на процесс измерения внешних факторов и может изменять свое значение.
Правила подсчета погрешностей
Для номинальной оценки погрешностей существует несколько правил:
- при сложении и вычитании чисел необходимо складывать их абсолютные погрешности;
- при делении и умножении чисел требуется сложить относительные погрешности;
- при возведении в степень относительную погрешность умножают на показатель степени.
Приближенные и точные числа записываются при помощи десятичных дробей. Берется только среднее значение, поскольку точное может быть бесконечно длинным. Чтобы понять, как записывать эти числа, необходимо узнать о верных и сомнительных цифрах.
Верными называются такие цифры, разряд которых превосходит абсолютную погрешность числа. Если же разряд цифры меньше абсолютной погрешности, она называется сомнительной. Например, для дроби 3,6714 с погрешностью 0,002 верными будут цифры 3,6,7, а сомнительными – 1 и 4. В записи приближенного числа оставляют только верные цифры. Дробь в этом случае будет выглядеть таким образом – 3,67.
Что мы узнали?
Абсолютные и относительные погрешности используются для оценки точности измерений. Абсолютной погрешностью называют разницу между точным и приближенным числом. Относительная погрешность – это отношение абсолютной погрешности числа к самому числу. На практике используют относительную погрешность, так как она является более точной.
Тест по теме
Доска почёта

Чтобы попасть сюда — пройдите тест.
-
Светлана Лобанова-Асямолова
10/10
-
Валерий Соломин
10/10
-
Анастасия Юшкова
10/10
-
Ксюша Пономарева
7/10
-
Паша Кривов
10/10
-
Евгений Холопик
9/10
-
Guzel Murtazina
10/10
-
Максим Аполонов
10/10
-
Olga Bimbirene
9/10
-
Света Колодий
10/10
Оценка статьи
4.2
Средняя оценка: 4.2
Всего получено оценок: 2187.
А какая ваша оценка?
Среднее арифметическое, как известно, используется для получения обобщающей характеристики некоторого набора данных. Если данные более-менее однородны и в них нет аномальных наблюдений (выбросов), то среднее хорошо обобщает данные, сведя к минимуму влияние случайных факторов (они взаимопогашаются при сложении).
Когда анализируемые данные представляют собой выборку (которая состоит из случайных значений), то среднее арифметическое часто (но не всегда) выступает в роли приближенной оценки математического ожидания. Почему приближенной? Потому что среднее арифметическое – это величина, которая зависит от набора случайных чисел, и, следовательно, сама является случайной величиной. При повторных экспериментах (даже в одних и тех же условиях) средние будут отличаться друг от друга.
Для того, чтобы на основе статистического анализа данных делать корректные выводы, необходимо оценить возможный разброс полученного результата. Для этого рассчитываются различные показатели вариации. Но то исходные данные. И как мы только что установили, среднее арифметическое также обладает разбросом, который необходимо оценить и учитывать в дальнейшем (в выводах, в выборе метода анализа и т.д.).
Интуитивно понятно, что разброс средней должен быть как-то связан с разбросом исходных данных. Основной характеристикой разброса средней выступает та же дисперсия.
Дисперсия выборочных данных – это средний квадрат отклонения от средней, и рассчитать ее по исходным данным не составляет труда, например, в Excel предусмотрены специальные функции. Однако, как же рассчитать дисперсию средней, если в распоряжении есть только одна выборка и одно среднее арифметическое?
Расчет дисперсии и стандартной ошибки средней арифметической
Чтобы получить дисперсию средней арифметической нет необходимости проводить множество экспериментов, достаточно иметь только одну выборку. Это легко доказать. Для начала вспомним, что средняя арифметическая (простая) рассчитывается по формуле:
где xi – значения переменной,
n – количество значений.
Теперь учтем два свойства дисперсии, согласно которым, 1) — постоянный множитель можно вынести за знак дисперсии, возведя его в квадрат и 2) — дисперсия суммы независимых случайных величин равняется сумме соответствующих дисперсий. Предполагается, что каждое случайное значение xi обладает одинаковым разбросом, поэтому несложно вывести формулу дисперсии средней арифметической:
Используя более привычные обозначения, формулу записывают как:
где σ2 – это дисперсия, случайной величины, причем генеральная.
На практике же, генеральная дисперсия известна далеко не всегда, точнее совсем редко, поэтому в качестве оной используют выборочную дисперсию:
Стандартное отклонение средней арифметической называется стандартной ошибкой средней и рассчитывается, как квадратный корень из дисперсии.
Формула стандартной ошибки средней при использовании генеральной дисперсии
Формула стандартной ошибки средней при использовании выборочной дисперсии
Последняя формула на практике используется чаще всего, т.к. генеральная дисперсия обычно не известна. Чтобы не вводить новые обозначения, стандартную ошибку средней обычно записывают в виде соотношения стандартного отклонения выборки и корня объема выборки.
Назначение и свойство стандартной ошибки средней арифметической
Стандартная ошибка средней много, где используется. И очень полезно понимать ее свойства. Посмотрим еще раз на формулу стандартной ошибки средней:
Числитель – это стандартное отклонение выборки и здесь все понятно. Чем больше разброс данных, тем больше стандартная ошибка средней – прямо пропорциональная зависимость.
Посмотрим на знаменатель. Здесь находится квадратный корень из объема выборки. Соответственно, чем больше объем выборки, тем меньше стандартная ошибка средней. Для наглядности изобразим на одной диаграмме график нормально распределенной переменной со средней равной 10, сигмой – 3, и второй график – распределение средней арифметической этой же переменной, полученной по 16-ти наблюдениям (которое также будет нормальным).
Судя по формуле, разброс стандартной ошибки средней должен быть в 4 раза (корень из 16) меньше, чем разброс исходных данных, что и видно на рисунке выше. Чем больше наблюдений, тем меньше разброс средней.
Казалось бы, что для получения наиболее точной средней достаточно использовать максимально большую выборку и тогда стандартная ошибка средней будет стремиться к нулю, а сама средняя, соответственно, к математическому ожиданию. Однако квадратный корень объема выборки в знаменателе говорит о том, что связь между точностью выборочной средней и размером выборки не является линейной. Например, увеличение выборки с 20-ти до 50-ти наблюдений, то есть на 30 значений или в 2,5 раза, уменьшает стандартную ошибку средней только на 36%, а со 100-а до 130-ти наблюдений (на те же 30 значений), снижает разброс данных лишь на 12%.
Лучше всего изобразить эту мысль в виде графика зависимости стандартной ошибки средней от размера выборки. Пусть стандартное отклонение равно 10 (на форму графика это не влияет).
Видно, что примерно после 50-ти значений, уменьшение стандартной ошибки средней резко замедляется, после 100-а – наклон постепенно становится почти нулевым.
Таким образом, при достижении некоторого размера выборки ее дальнейшее увеличение уже почти не сказывается на точности средней. Этот факт имеет далеко идущие последствия. Например, при проведении выборочного обследования населения (опроса) чрезмерное увеличение выборки ведет к неоправданным затратам, т.к. точность почти не меняется. Именно поэтому количество опрошенных редко превышает 1,5 тысячи человек. Точность при таком размере выборки часто является достаточной, а дальнейшее увеличение выборки – нецелесообразным.
Подведем итог. Расчет дисперсии и стандартной ошибки средней имеет довольно простую формулу и обладает полезным свойством, связанным с тем, что относительно хорошая точность средней достигается уже при 100 наблюдениях (в этом случае стандартная ошибка средней становится в 10 раз меньше, чем стандартное отклонение выборки). Больше, конечно, лучше, но бесконечно увеличивать объем выборки не имеет практического смысла. Хотя, все зависит от поставленных задач и цены ошибки. В некоторых опросах участие принимают десятки тысяч людей.
Дисперсия и стандартная ошибка средней имеют большое практическое значение. Они используются в проверке гипотез и расчете доверительных интервалов.
Поделиться в социальных сетях:
Загрузить PDF
Загрузить PDF
Стандартной ошибкой называется величина, которая характеризует стандартное (среднеквадратическое) отклонение выборочного среднего. Другими словами, эту величину можно использовать для оценки точности выборочного среднего. Множество областей применения стандартной ошибки по умолчанию предполагают нормальное распределение. Если вам нужно рассчитать стандартную ошибку, перейдите к шагу 1.
-
1
Запомните определение среднеквадратического отклонения. Среднеквадратическое отклонение выборки – это мера рассеянности значения. Среднеквадратическое отклонение выборки обычно обозначается буквой s. Математическая формула среднеквадратического отклонения приведена выше.
-
2
Узнайте, что такое истинное среднее значение. Истинное среднее является средним группы чисел, включающим все числа всей группы – другими словами, это среднее всей группы чисел, а не выборки.
-
3
Научитесь рассчитывать среднеарифметическое значение. Среднеаримфетическое означает попросту среднее: сумму значений собранных данных, разделенную на количество значений этих данных.
-
4
Узнайте, что такое выборочное среднее. Когда среднеарифметическое значение основано на серии наблюдений, полученных в результате выборок из статистической совокупности, оно называется “выборочным средним”. Это среднее выборки чисел, которое описывает среднее значение лишь части чисел из всей группы. Его обозначают как:
-
5
Усвойте понятие нормального распределения. Нормальные распределения, которые используются чаще других распределений, являются симметричными, с единичным максимумом в центре – на среднем значении данных. Форма кривой подобна очертаниям колокола, при этом график равномерно опускается по обе стороны от среднего. Пятьдесят процентов распределения лежит слева от среднего, а другие пятьдесят процентов – справа от него. Рассеянность значений нормального распределения описывается стандартным отклонением.
-
6
Запомните основную формулу. Формула для вычисления стандартной ошибки приведена выше.
Реклама
-
1
Рассчитайте выборочное среднее. Чтобы найти стандартную ошибку, сначала нужно определить среднеквадратическое отклонение (поскольку среднеквадратическое отклонение s входит в формулу для вычисления стандартной ошибки). Начните с нахождения средних значений. Выборочное среднее выражается как среднее арифметическое измерений x1, x2, . . . , xn. Его рассчитывают по формуле, приведенной выше.
- Допустим, например, что вам нужно рассчитать стандартную ошибку выборочного среднего результатов измерения массы пяти монет, указанных в таблице:
Вы сможете рассчитать выборочное среднее, подставив значения массы в формулу:
- Допустим, например, что вам нужно рассчитать стандартную ошибку выборочного среднего результатов измерения массы пяти монет, указанных в таблице:
-
2
Вычтите выборочное среднее из каждого измерения и возведите полученное значение в квадрат. Как только вы получите выборочное среднее, вы можете расширить вашу таблицу, вычтя его из каждого измерения и возведя результат в квадрат.
- Для нашего примера расширенная таблица будет иметь следующий вид:
-
3
Найдите суммарное отклонение ваших измерений от выборочного среднего. Общее отклонение – это сумма возведенных в квадрат разностей от выборочного среднего. Чтобы определить его, сложите ваши новые значения.
- В нашем примере нужно будет выполнить следующий расчет:
Это уравнение дает сумму квадратов отклонений измерений от выборочного среднего.
- В нашем примере нужно будет выполнить следующий расчет:
-
4
Рассчитайте среднеквадратическое отклонение ваших измерений от выборочного среднего. Как только вы будете знать суммарное отклонение, вы сможете найти среднее отклонение, разделив ответ на n -1. Обратите внимание, что n равно числу измерений.
- В нашем примере было сделано 5 измерений, следовательно n – 1 будет равно 4. Расчет нужно вести следующим образом:
-
5
Найдите среднеквадратичное отклонение. Сейчас у вас есть все необходимые значения для того, чтобы воспользоваться формулой для нахождения среднеквадратичного отклонения s.
- В нашем примере вы будете рассчитывать среднеквадратичное отклонение следующим образом:
Следовательно, среднеквадратичное отклонение равно 0,0071624.
Реклама
- В нашем примере вы будете рассчитывать среднеквадратичное отклонение следующим образом:
-
1
Чтобы вычислить стандартную ошибку, воспользуйтесь базовой формулой со среднеквадратическим отклонением.
- В нашем примере вы сможете рассчитать стандартную ошибку следующим образом:
Таким образом в нашем примере стандартная ошибка (среднеквадратическое отклонение выборочного среднего) составляет 0,0032031 грамма.
- В нашем примере вы сможете рассчитать стандартную ошибку следующим образом:
Советы
- Стандартную ошибку и среднеквадратическое отклонение часто путают. Обратите внимание, что стандартная ошибка описывает среднеквадратическое отклонение выборочного распределения статистических данных, а не распределения отдельных значений
- В научных журналах понятия стандартной ошибки и среднеквадратического отклонения несколько размыты. Для объединения двух величин используется знак ±.
Реклама
Об этой статье
Эту страницу просматривали 49 292 раза.



 и выберите Параметры Excel > Формулы.
и выберите Параметры Excel > Формулы.
 на панели быстрого доступа.
на панели быстрого доступа.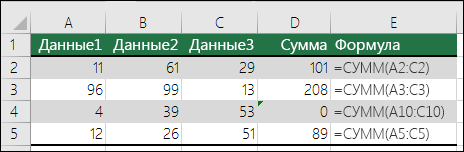

 , а затем выберите нужный параметр. Доступные команды различаются для каждого типа ошибки, и первая запись описывает ошибку.
, а затем выберите нужный параметр. Доступные команды различаются для каждого типа ошибки, и первая запись описывает ошибку.