Цель занятия: дать представление об осевой
симметрии; научить находить осевую симметрию в фигурах.
Задачи:
- развивать умение видеть симметричные фигуры, различать
фигуры, имеющие одну или несколько осей симметрии; - формировать умение проводить практическими и графическими
способами оси симметрии в фигурах; - воспитывать интерес к математике, чувство взаимовыручки,
любознательность, аккуратность.
Формируемые УУД:
-
регулятивные: принимать и сохранять цели и задачи
учебной деятельности, искать и находить средства их
достижения; планировать, контролировать и оценивать действия
в соответствии с поставленной задачей; -
познавательные: выделять существенные характеристики
объекта; осуществлять поиск и выделять необходимую информацию
для выполнения заданий; -
коммуникативные: строить речевое высказывание в
устной форме; принимать участие в определении общей цели и
путей ее достижения; признавать возможность существования
различных точек зрения; -
личностные: осуществлять самоконтроль и самооценку
результатов деятельности; применять умения и навыки
самостоятельной деятельности, осознавать личную
ответственность за ее результат.
Методическое оснащение: ПК, интерактивная
доска, презентация, у каждого ученика: одна из геометрических
фигур (квадрат, прямоугольник, равносторонний и прямоугольный
треугольники, круг), линейка, ножницы, цветная бумага; карточки
с заданиями.
Ход урока
1. Организационный момент
Добрый день, ребята. Мы начинаем урок «Математика и
конструирование». Пусть сегодняшний урок принесёт нам радость
общения. Сегодня на уроке вас ожидает много интересных заданий
и новых открытий! А вашими помощниками пусть будут внимание,
целеустремлённость и ваша активная деятельность.
2. Мотивирование к учебной деятельности
(Мозговой штурм)
— А знаете ли вы, что …
— Название фигуры Трапеция происходит от латинского слова
«Трапезиум» — столик. От этого же слова происходит слово
«трапеза»
— А знаете ли вы, что…
— Во время сна рост увеличивается на 8 мм. Но после пробуждения
он «возвращается» к прежним цифрам.
— А знаете ли вы, что …
— Пчёлы — отличные «математики». Они изобрели самую совершенную
геометрическую форму сот -шестигранник, что обеспечило
наивысшую прочность этих хрупких восковых строений и
исключительную экономию места.
— А знаете ли вы, что …
— Число 111 111 магическое! При умножении его на само себя
получается такой лёгкий ответ 12 345 654 321.
— А знаете ли вы, что …
— 90% информации человек получает при помощи глаз. Отсюда и
пошло выражение «Лучше один раз …»
3. Актуализация знаний
— Посмотрите небольшой видео-ролик и найдите закономерность.
— Что интересного вы заметили? (отражение в воде)
— А где еще отражаются предметы? (В зеркале).
— Подумайте, как в математике называется зеркальное
отображение? (СИММЕТРИЯ)
— Отлично! Сформулируйте тему урока. (или нам поможет ребус).
(Слайд Симметрия.)
А как вы понимаете, что такое «симметрия» ???
— Тогда Давайте поставим перед собой цель урока.
ЦЕЛЬ — узнать, что такое «симметрия», где
встречается.
— Где можно ознакомиться с этим понятием? (посмотреть в
толковом словаре — ПОКА СМОТРЯТ)
— Назовите предметы, которые вы считаете СИММЕТРИЧНЫМИ. (запись
на доске) не знаем…, не уверенны…
— Давайте обратимся к толковому словарю и выясним значение
этого слова. (Толковый словарь С.И.Ожегова: «Симметрия» — это
соразмерность, одинаковость в расположении частей, В.И. Даля —
сходность, одинаковость 2-х половин…..)
— В переводе с греческого языка симметрия звучит как
«гармония», означая красоту.
Симметрия придает гармоничность, законченность.
4. Практическая работа. Введение в новую тему «Ось
симметрии»
Исследование квадрата.
— Давайте проверим это утверждение! что СИММЕТРИЯ — это
ОДИНАКОВОСТЬ и СХОДНОСТЬ 2-х ПОЛОВИН!!!
— У вас на столе лежат квадраты.
— Сложите квадрат пополам и четко прогладим линию сгиба.
— Покажите! Что мы наблюдаете?
— Какие получились части квадрата? (Одинаковые)
— Обведите цветным карандашом получившуюся прямую. Это и есть
ось симметрии!
— Сравните левую и правую части от оси симметрии. — Сделайте
вывод.
— Мы получили две одинаковые части слева и справа от линии
сгиба. В этом случае линия сгиба будет осью
симметрии, а части, расположенные по обе стороны от
нее, будут симметричными. А фигура называется —
симметричная.
Вывод: в квадрате мы нашли ось
симметрии. Ось симметрии делит фигуру на одинаковые
равные части. Эти половинки совпадают.
— Давайте попробуем сложить квадрат вновь пополам, но
по-другому.
— Что получили? — Покажите! (ещё одну ось симметрии)
— Обведите эту линию.
— Как еще можно сложить квадрат? (по диагонали)
— Так сколько же осей симметрии у квадрата? (4)
— Правильно! Запишем это в таблицу
5. Физминутка (рисуем руками в воздухе)
Много ль надо нам, ребята,
Для умелых наших рук?
Нарисуем 2 квадрата,
А на них огромный круг.
А потом ещё кружочек,
Треугольный колпачок.
Вот и вышел очень, очень
Развесёлый чудачок!
— Подойдите к окну, Пусть отдохнут ваши глаза, посмотрите по
сторонам, полюбуйтесь красотой зимнего дня. Возможно, вы
увидите симметричные предметы.…. Перечислите. Продолжаем
работать!
6. Работа в группах
Исследование разных геометрических фигур.
Защита.
Ребята, предлагаю вам провести исследование — симметричны ли
другие геом. фигуры? Работать будем в группах. Вспомним правила
работы в группах.
— Каждый должен работать на общий результат.
— Один говорит, другие слушают.
— Своё несогласие высказывай вежливо.
— Распределить обязанности.
В конвертах №1 у вас лежат геометрические фигуры. (Для каждой
группы — разные.)
Ваша задача узнать, симметрична ли фигура? сколько осей
симметрии имеет геом. фигура? Выступать будет один
представитель от группы. Вам дается 1 мин на исследование. И 1
мин на выступление. Используете алгоритм для выступления №1. (и
демонстрирует на большой фигуре.)
— Возьмите фигуры из конверта. Приступайте к исследованию.
— Что нужно сделать, чтобы провести ось симметрии? (перегнуть
фигуры пополам)
— Проведите оси симметрии, если это возможно. Цветным
карандашом.
Итак,
— Слушаем представителя 1-й группы.
— Приглашаем представителя 2-й группы.
— Слушаем представителя 3-й группы.
— Слушаем представителя 4-й группы. (На доске заполняю
результаты исследований в таблице)
ИТОГ. МОЛОДЦЫ. ВСЕ ГРУППЫ СПРАВИЛИСЬ С 1 ЗАДАНИЕМ.
— Назовите самую «несимметричную» фигуру. (Прям. Треугольник)
— Назовите самую «симметричную» фигуру. (круг)
— В Древней Греции круг считался венцом совершенства.
И не случайно! У него больше всего осей симметрий!
7. Исследование в разных областях. Защита
— Мы выяснили, что в математике, не у всех фигур, но симметрия
существует. Только ли в этой области она может быть?
— Оказывается, все в мире, всё построено по принципу симметрии.
Древние греки считали, что Вселенная симметрична просто потому,
что симметрия прекрасна. Используя красоту и гармонию природы,
человек многое создал в мире симметрии своими
руками. Об этих и многих других предметах мы сейчас и
поговорим.
— Продолжим нашу исследовательскую работу.
— Каждой группе нужно провести исследование — в своей области.
Ваша задача — доказать, или опровергнуть
наличие симметричности и, конечно же, сделать выводы о
проделанной работе. Вам достаточно 2 мин. обсудить этот вопрос
И 1 мин на защиту.
— Возьмите конверт №2. Ознакомьтесь с темой исследования.
Приступайте к работе. Защита по алгоритму.
- 1 гр. — Симметрия в архитектуре
- 2 гр. — Симметрия в мире растений
- 3 гр. — Симметрия в русском языке
- 4 гр. — Симметрия в мире животных
(Выступления групп. Выводы. Заполнение таблицы на доске.)
ИТОГ. МОЛОДЦЫ. ВСЕ ГРУППЫ СПРАВИЛИСЬ С 2 ЗАДАНИЕМ.
— Итак, мы доказали, что Симметрия- это не только красота.
Симметричность формы нужна рыбе, чтобы плыть, птице, чтобы
летать. Поэтому мы можем сделать вывод, что симметрия в природе
неспроста: она ещё и полезна, т.е. целесообразна.
— Рассматривая красивую машину, величественную фигуру самолёта,
корабли — мы восхищаемся ими ! И в основе их красоты лежит
симметрия. Денис из нашего класса своими руками создаёт эти
шедевры!
— К какой области можно отнести эти предметы, созданные руками
человека?
8. Подведение итогов «Кластер». Оценивание
— Какие цели мы ставили в начале урока? …(Что такое симметрия?
Где встречается?)
— Что вы выяснили для себя?
— Какие слова, словосочетания, связи, явления события … и т.д.
возникают с этой темой?
(заполним «КЛАСТЕР»)
ИТОГ! — Каждая группа справилась с
исследованием, правильно сделали выводы! Активно работали на
уроке…. Молодцы!
Домашнее задание
— Ребята, это не все ОБЛАСТИ, где ВСТРЕЧАЕТСЯ СИММЕТРИЯ.
Подумайте дома, подготовьте картинку, в какой области можно
встретить симметрию. (Спорт, искусство,…и т.д.)
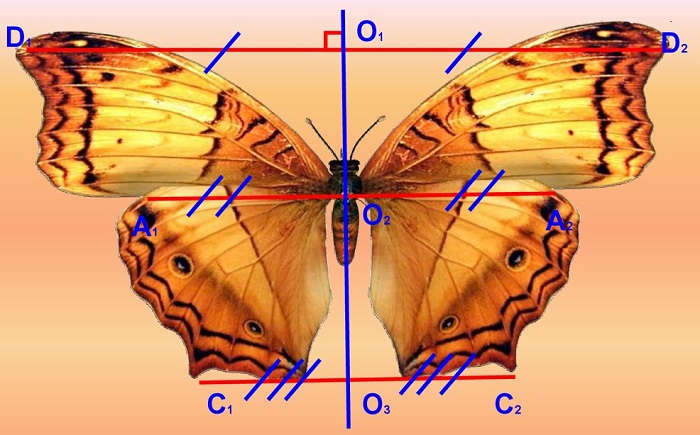
— Символом симметрии является БАБОЧКА.
Я предлагаю вам создать уникальный узор на крыльях бабочки или
выполнить другой симметричный рисунок на выбор. Подойдите,
возьмите, что вам больше нравится.
— Рассмотрите иллюстрацию к мультфильму. Что увидел Енот в
пруду?
— А можно ли проверить, доказать, СИММЕТРИЧНЫ ли предметы из
повседневной жизни, крупные, твёрдые… НЕ
бумажные?..
— Способ — сложением пополам — не всегда действует. Можно
провести прямую «на глаз».
Урок окончен. Спасибо, вы молодцы!
Что такое осевая симметрия? Само слово «симметрия» имеет греческие корни и говорит о существующем определенном порядке расположения частей некого предмета, а также о его соразмерности.
Под симметрией понимается такое качество предметов, что их можно совместить друг с другом при некоторых преобразованиях.
Что такое симметрия
Наиболее часто это понятие встречается в геометрии. Объект считается симметричным, если после некоторых геометрических преобразований он смог сохранить свои первоначальные свойства.
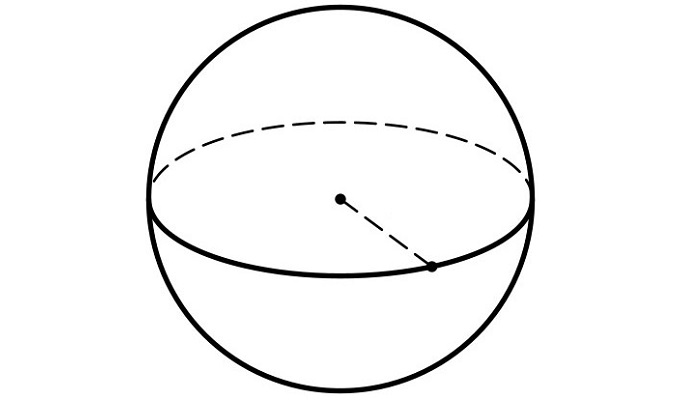
В качестве примера стоит рассмотреть обычный круг. Если его вращать вокруг условного центра, он сохранит свою форму и первоначальные характеристики. Поэтому этот геометрический предмет смело можно назвать симметричным.
Виды симметрии определяются возможными преобразованиями для данного объекта и его свойствами, которые в результате проведенных манипуляций должны сохраниться. В случае, когда это условие не соблюдается, можно утверждать о наличии асимметрии.
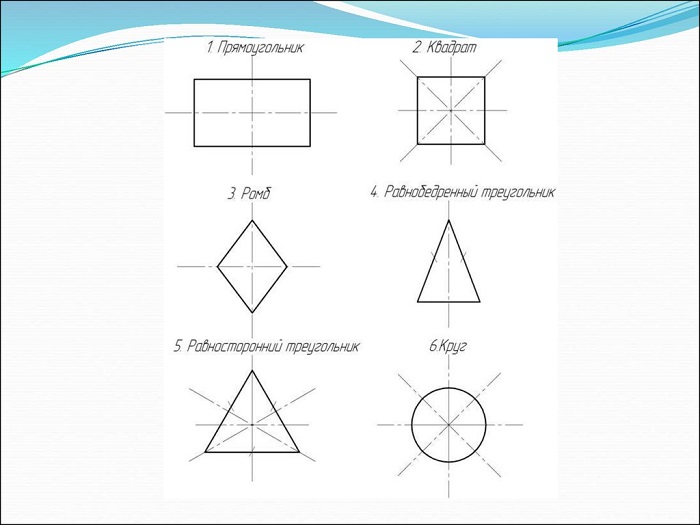
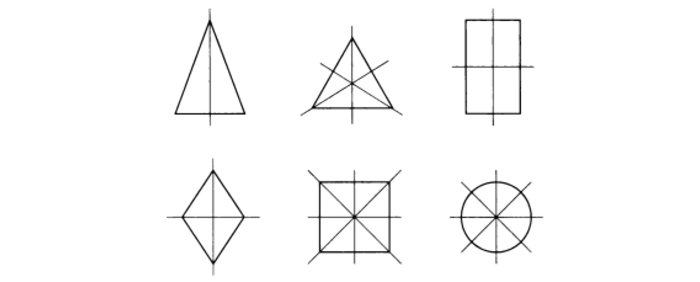
Рис. 1 Фигуры, обладающие симметричностью
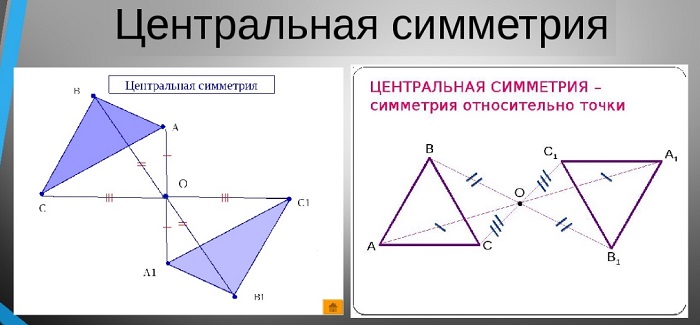
Центральная симметрия
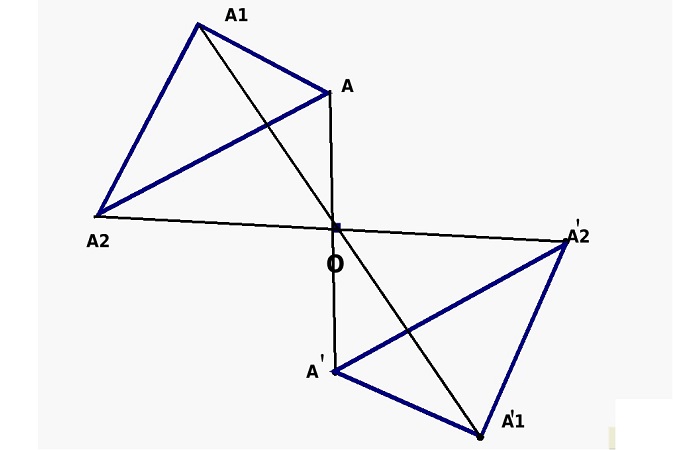
Это явление относительно некой точки. Она представляет собой преобразование множества точек пространства или поверхности, во время которого ее центр всегда постоянен и не меняет своего положения.
Данный вид симметрии предполагает, что на равном расстоянии от ее центра располагаются два предмета, например, две точки. Если провести между ними условную прямую, они будут располагаться на ее противоположных концах, а середина этой прямой и будет являться осевым центром.
Если считать центр неподвижным и начать преобразовывать прямую (т. е. вращать ее относительно центральной точки), то точки на ее концах опишут две кривые. Все точки одной кривой будут иметь такие же симметричные точки на другой кривой.
Объекты, обладающие центром симметрии, представляют большой интерес для ученых. В геометрии насчитывается достаточно много таких объектов. К ним относятся прямые, отрезки, окружность, прямоугольник и др. Центрально симметричные объекты встречаются и в природе.
Рис. 2 Графическое представление центральной симметрии
Осевая симметрия
Это симметрия относительно прямой. В данном классе две точки симметричны относительно некой прямой, если она пересекает центр отрезка, соединяющего эти две точки и является перпендикуляром к нему. Любая точка прямой симметрична сама себе.
Рис. 3 Наглядное представление осевой симметрии
Объект симметричен относительно прямой, если все его точки имеют такие же симметричные аналоги относительно этой прямой. Она же — центр симметрии.
В качестве наглядно примера можно взять обычный бумажный лист, если его сложить пополам. Если через линию сгиба провести прямую – это и будет центром.
Определенная точка одной половины листы имеет такую же симметричную точку на другой его части, расположенную на перпендикуляре на таком же расстоянии от осевой линии. Одна часть листа тетради является по сути зеркальным отображением другой.
Рис. 4 Примеры осевой симметрии
Фигуры, имеющие несколько осей симметрии
Есть предметы и геометрические фигуры с некоторым числом осей. Для начала в качестве примера стоит рассмотреть прямоугольник и ромб, которые имеют две такие оси.
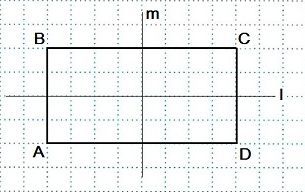
Две оси симметрии характерны для прямоугольника. Это прямые, которые проведены через точки, являющиеся серединами его противоположных сторон.
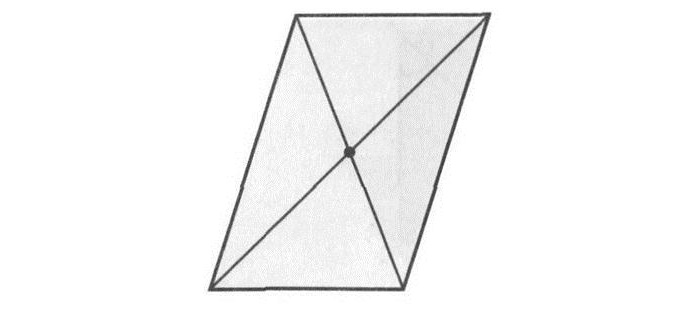
То же самое (наличие двух осей) присуще и ромбу. Оси являются прямыми, содержащими диагонали данной геометрической фигуры.
Интерес представляет и квадрат, у которого насчитывается четыре оси. Данная фигура является одновременно и ромбом, и прямоугольником. Остальные виды параллелограммов не имеют осей симметрии вообще.
Рис. 5 Оси симметрии ромба
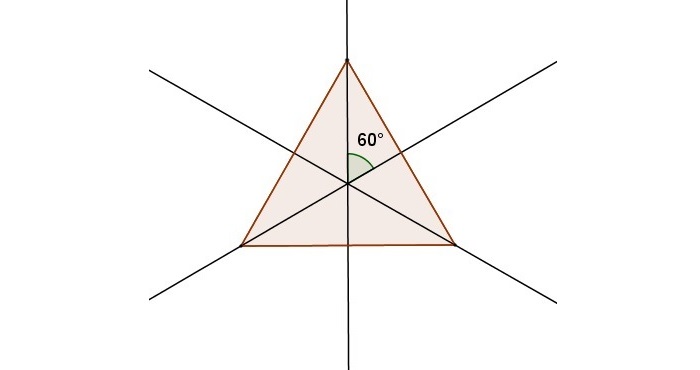
Единственной фигурой, у которой есть три оси симметрии, является равносторонний треугольник. Они представляют собой не что иное, как его медианы, линии соединяющие середины его сторон. Медианы равностороннего треугольник – это его и биссектрисы, и высоты.
Рис. 6 Оси симметрии равностороннего треугольника
В обычной жизни многие даже не задумываются о том, как часто они сталкиваются с различными видами симметрии. Это понятие характерно не только для мира математики.
Симметрия встречается в мире природы, архитектуре, в мире искусства и композиции, а также в других сферах человеческой жизни.
Осознание данного факта прошло долгий путь во времени, над ним задумывались великие умы на протяжении многих столетий. С древних времен и до настоящего времени определение этого понятия прошло долгий путь развития.
>
>
Муниципальное
бюджетное общеобразовательное учреждение города Ульяновска «Средняя школа №
42»
Семенова Анна
Николаевна
учитель
начальных классов
Методическая
разработка занятия внеурочной деятельности курса
«Математика
и конструирование»
4 класс
Тема: «Осевая
симметрия»
Тема: «Осевая симметрия»
Цель
занятия: дать
представление об осевой симметрии; научить находить осевую симметрию в фигурах.
Задачи:
·
развивать умение видеть симметричные
фигуры, различать фигуры, имеющие одну или несколько осей симметрии;
·
формировать умение
проводить практическими и графическими способами оси симметрии в
фигурах;
·
воспитывать интерес к математике, чувство
взаимовыручки, любознательность, аккуратность.
Формируемые
УУД:
—
регулятивные: принимать и сохранять цели и задачи учебной деятельности,
искать и находить средства их достижения; планировать, контролировать и
оценивать действия в соответствии с поставленной задачей;
—
познавательные: выделять существенные характеристики объекта;
осуществлять поиск и выделять необходимую информацию для выполнения заданий;
—коммуникативные:
строить речевое высказывание в устной форме; принимать участие в определении
общей цели и путей ее достижения; признавать возможность существования
различных точек зрения;
—личностные:
осуществлять самоконтроль и самооценку результатов деятельности; применять
умения и навыки самостоятельной деятельности, осознавать личную ответственность
за ее результат.
Методическое
оснащение: ПК, интерактивная доска, презентация, у каждого ученика: одна из
геометрических фигур (квадрат, прямоугольник, равносторонний и прямоугольный
треугольники, круг), линейка, ножницы, цветная бумага; карточки с заданиями.
План
занятия
1.
Организационный момент.
2.
Самоопределение к деятельности
3.
Работа по теме занятия
4.
Физкультминутка
5.
Закрепление изученного
6.
Рефлексия
7.
Подведение итогов занятия
Ход занятия
I.Организационный
момент
Учащиеся
поделены на группы
Учитель.
Давайте улыбнемся друг другу.
Начинайте
день с улыбки
С
добрым сердцем и тогда
Будет
радость и удача
Вам
сопутствовать всегда!
Пусть
улыбки и хорошее настроение будут верными спутниками на сегодняшнем занятии и
помогут разобраться во всем и справиться с любой задачей.
II.Самоопределение к
деятельности
Учитель.
Посмотрим отрывок из мультфильма «Крошка Енот» и
вспомним, какому герою помогла улыбка (Слайд 2) (Крошке Еноту)
Учитель.
Рассмотрите иллюстрацию к мультфильму. (Слайд 3)
Учитель.
Что увидел Енотик в пруду? (Свое отражение)
Учитель.
Что вы можете сказать об изображении Енота и его отображении в воде? (Отображение
получилось перевернутое.)
Учитель.
Изменились ли правая и левая сторона? (Нет).
Учитель.
Ребята, а где еще отражаются предметы? (В зеркале).
Учитель.
Чтобы узнать, как называется зеркальное
отображение в математике, нам нужно разгадать ребус. (Слайд
4) (Симметрия.)
Учитель.
Сформулируйте тему и задачи занятия. (Тема — симметрия.
Задачи: узнать, что такое «симметрия», где встречается симметрия.)
Учитель. Сегодня
на занятии мы прикоснемся к удивительному математическому понятию «симметрия».
Узнаем, что такое симметрия, ось симметрии. Научимся строить симметричные
фигуры. Узнаем, где встречается симметрия.
III.Работа
по теме занятия
Учитель.
— Так что же означает слово «симметрия»? Давайте
обратимся к словарю и выясним значение этого слова. (Словарь С.И. Ожегова:
«Симметрия – соразмерность, пропорциональность в расположении частей
чего-нибудь».)
Учитель.
Слово «симметрия» в переводе с греческого звучит как
«гармония», означая красоту, соразмерность, пропорциональность, одинаковость в
расположении частей.
Учитель.
Возьмите лист, на котором изображен треугольник (№1).
Обведите треугольник 2-3 раза, сильно нажимая на карандаш.
Перегните
лист пополам так, чтобы треугольник оказался внутри.
Не
разгибая лист, снова обведите треугольник, сильно нажимая на карандаш.
Раскройте
лист. Что у вас получилось? (Два треугольника)
Учитель.
По линии сгиба проведите по линейке прямую.
Учитель.
Линия сгиба будет осью симметрии этих двух треугольников.
Учитель.
Если снова согнуть лист по оси симметрии (линии сгиба),
что произойдет с треугольниками? (Они совпадут.)
Учитель. Как мы называем
фигуры, которые совпадают? (Равными.)
Учитель.
Что интересного заметили в расположении треугольников относительно
линии сгиба. (Они расположены на одинаковом расстоянии относительно линии
сгиба.)
Учитель.
Возьмите лист бумаги (№2). Что с ним нужно сделать с
листочком, чтобы получить симметричную фигуру? (Сложить пополам)
Учитель.
Перегните его пополам и хорошо разгладьте линию сгиба.
Учитель.
Приложите шаблон к линии сгиба, обведите его (елочку).
Вырежьте
силуэт, не перерезая линию сгиба. Расправьте лист. Что у вас получилось? (Елочка)
Учитель.
Что вы можете сказать о правой и левой частях елочки (Они
одинаковые.)
Учитель.
В
этом случае линия сгиба будет осью симметрии, а части елочки,
расположенные по обе стороны от нее, будут симметричными относительно
этой оси.
Работа в группах
Учитель. Вы разделены на группы. Вспомните правила работы в группе. (1.
В группе должен быть ответственный; 2. Работать должен каждый на общий
результат; 3. Один говорит, другие слушают; 4. Своё несогласие высказывай
вежливо; 5. Если не понял, переспроси) (Слайд 6)
Учитель. Выберите
руководителя группы, который будет следить за выполнением задания.
Учитель. В конвертах №3 у вас лежат геометрические фигуры. У одной
группы квадраты, у другой прямоугольники, у третьей по два треугольника, у
четвертой круги. Руководители группы раздайте фигуры.
Учитель. Что нужно сделать, чтобы провести ось симметрии? (Перегнуть
фигуры пополам.)
Учитель. Возьмите фигуры и проведите, если это возможно, оси симметрии в
данных фигурах. После выполнения задания ответьте на вопросы: «Симметрична
фигура или нет? Сколько осей симметрии можно провести?»
Учитель.
Рассмотрим квадрат. Симметричен ли он? (Да). (Слайд 7)
Учитель.
Докажите! (Если перегнуть квадрат пополам, то две половинки совпадут.)
Учитель.
Сколько осей симметрии у квадрата? (Четыре).
Учитель.
Рассмотрим прямоугольник. Симметричен ли он? (Да). (Слайд 
Учитель.
Докажите! (Если перегнуть прямоугольник пополам, то две половинки совпадут.)
Учитель.
Сколько осей симметрии у прямоугольника? (Две).
Учитель. Рассмотрим
треугольники. Какие это треугольники, если измерить длины сторон этих
треугольников? (Равносторонний и разносторонний.)
Учитель.
Рассмотрим равносторонний треугольник Симметричен ли он? (Да).
Учитель.
Почему вы так считаете? (Если перегнуть его пополам, то обе половинки
совпадут).
Учитель. Сколько
осей симметрии у этого треугольника? (Три). (Слайд 9)
Учитель.
А теперь проверим разносторонний треугольник. Симметричен ли он? (Нет).
Учитель.
Почему? (При перегибании половинки не совпадают).
Учитель.
Рассмотрим круг. Является ли круг симметричной фигурой. (Да)
Учитель.
А сколько у него осей симметрии? (Много). (Слайд 10)
Учитель.
Еще в Древней Греции круг считался венцом совершенства. И не случайно. У него
больше всего осей симметрии.
Учитель. Давайте
сделаем вывод. Что можете сказать о каждой фигуре? Все ли фигуры имеют
оси симметрии? (Выступает один представитель от
группы. 1 группа: квадрат – симметричная фигура, имеет четыре оси симметрии; 2
группа: прямоугольник – симметричная фигура, имеет две оси симметрии;
равносторонний треугольник – симметричная фигура, имеет три оси симметрии; разносторонний
треугольник – несимметричная фигура, не имеет ни одной оси симметрии; круг –
симметричная фигура, имеет много осей симметрии;).
IV.Физкультминутка
(Слайд 11)
«Мы
пойдем налево, мы пойдем направо»
V.Закрепление
изученного
Учитель.
Мы выяснили, что в математике встречается симметрия.
Но только ли в этой науке она может быть?
Работа
в группах
Учитель.
Чтобы ответить на этот вопрос проведем исследование.
Каждая группа получает свой маршрутный лист. (Конверт №4)
Учитель.
Выполнив задание, прикрепите его на доску с помощью
магнита и приготовьтесь к защите. Алгоритм выступления у вас на парте. Во время
выполнения задания вы можете пользоваться справочниками, энциклопедиями и
словарями.
Темы вслух не оглашаются.
Дети
получают маршрутные листы (Приложение 1) и выполняют задания в группах (Приложение
2).
Учитель.
Руководителя группы, которая работала над этой темой
(учитель показывает название темы), прошу приступить к защите. Итак, тема
вашего задания …
(1
группа. Тема нашего задания «Симметрия в мире животных». Каждое животное
(насекомое, рыба, птица, зверь, …) состоит из двух половин – левой и правой.
Поэтому у них симметричны правое и левое ухо, правый и левый глаз, правая и
левая лапа, правый и левый рог, …). Значит можно сделать вывод, что симметрия встречается
в животном мире.
2
группа. Тема нашего задания «Симметрия в мире растений». Симметрия хорошо видна на примере деревьев, их листьев,
симметрию можно увидеть среди цветов. Значит можно сделать вывод, что симметрия
встречается в растительном мире.
3
группа. Тема нашего задания «Симметрия в архитектуре». У многих архитектурных сооружений правая
сторона похожа на левую. В них можно провести ось симметрии. Значит
можно сделать вывод, что симметрия встречается в архитектуре.
4
группа. Тема нашего задания «Симметрия в русском языке». В русском языке
встречаются буквы, имеющие одну или две оси симметрии, есть буквы, которые не
имеют оси симметрии. Также в русском языке встречаются слова и целые предложения,
которые имеют ось симметрии. Такие слова и предложения называются палиндромами.
Значит, можно сделать вывод, что симметрия встречается в русском языке.)
На
доске возле стрелочек прикреплены выполненные
задания, некоторые стрелочки остаются пустыми:
 |
|||
 |
|||
Симметрия
вокруг
нас
Учитель.
Как вы думаете, почему остались пустые
стрелочки? (Симметрия может встречаться не только в указанных группах.)
Учитель.
Где же может еще встречаться симметрия?
(в технике, в спорте, в танце, в искусстве, …) (Слайд
12-15)
VI.Рефлексия
(Слайд 16)
Учитель.
Продолжите предложения:
Сегодня я узнал…
Я понял, что…
Теперь я могу…
Я научился…
У меня получилось…
Я попробую…
Меня удивило…
Мне захотелось…
Расскажу дома, что …
VII.Подведение
итогов занятия
Учитель.
Как называется тема, над которой мы
работали? (Симметрия)
Учитель. Какие фигуры
можно назвать симметричными? (Фигуры, имеющие ось симметрии и совпадающие
при перегибании).
Учитель.
Что такое ось симметрии? (Прямая линия,
по которой можно сложить фигуру, её половинки совпадут.)
Учитель.
Где можно встретить симметрию? (В архитектуре, в математике, в природе, в русском языке,
в технике, в музыке, в изобразительном искусстве)
Список литературы
1.
Волкова С.И. Математика и
конструирование. 4 класс. Учебное пособие для общеобразовательных организаций.
– М.: Просвещение, 2018.
2.
Жильцова Т.В., Обухова Л.А. Поурочные
разработки по наглядной геометрии: 1-4 классы. – М.: ВАКО. 2004.
3.
Ожегов С.И. и Шведова Н.Ю.
Толковый словарь русского языка: 80000 слов и фразеологических выражений. – М.:
Азбуковник, 1997.
4.
Рудницкая В.Н. Математика: 1
класс: учебник для учащихся общеобразовательных учреждений: в 2 ч. Ч.2 – М.:
Вентана-Граф, 2012.
Интернет-источники:
1.
https://urokimatematiki.ru/konspekt—uroka—s—prezentaciey—na—temu—simmetriya—klass-4255.html
2.
https://multiurok.ru/files/priezientatsiia—po—informatikie—na—tiemu—simmietriia-2-klass.html
3.
https://videouroki.net/catalog/4?utm_source=kopilka&utm_medium
4.
https://infourok.ru/?doc_dwn=478857
5.
https://nsportal.ru/nachalnaya—shkola/obshchepedagogicheskie—tekhnologii/2013/06/03/priemy—refleksii—na—urokakh—v
Приложение 1
Маршрутные листы:
1
группа. Симметрия в мире животных.
·
На белой бумаге перед вами – контур
бабочки. Проведите ось симметрии, раскрасьте бабочку в соответствии с правилами
симметрии.
·
Провести оси симметрии у данных животных.
·
Приведите свои примеры симметрии у
животных (2-3 примера).
2
группа. Симметрия в мире растений.
·
Перед вами – одна половинка известного
всем растения, вторая его половинка рассыпалась в виде мозаики. Склейте
растение и проведите оси симметрии.
·
Провести оси симметрии у данных растений.
·
Приведите свои примеры симметрии у
растений (2-3 примера).
3
группа. Симметрия в мире архитектуры.
·
Достроить с учетом линии симметрии по
клеточкам замок.
·
Провести оси симметрии у данных памятников
архитектуры.
·
Приведите свои примеры симметрии в
архитектуре (2-3 примера).
4
группа. Симметрия в русском языке и.
·
Вспомнить и записать 3 слова-палиндрома (слова,
читаемые слева направо и справа налево одинаково). Определить у них оси
симметрии.
·
Провести оси симметрии у данных букв
русского языка и разбить их на группы:
1
ось симметрии;
2
оси симметрии;
нет
осей симметрии.
·
Приведите примеры фраз-палиндромов (2-3).
Приложение 2
Симметрия
в мире животных


Симметрия
в мире растений
Анютины
глазки


Симметрия
в мире архитектуры
«Математика и конструирование» 4 класс
Учитель начальных классов МБОУ «СОШ №1» п.Пуровск Пуровского района
Исаева Светлана Геннадьевна
Тема: Осевая симметрия
Цель: формирование понятия осевая симметрия
Планируемые результаты
Предметные умения:
— закрепить знания о понятии «симметрия»;
— уметь выделять, конструировать;
— указывать ось симметрии;
— анализировать и решать проблемы;
Личностные УУД:
— устанавливать связь между целью учебной деятельности и ее мотивом;
— определять общие для всех правила поведения;
— определять правила работы в парах, группах;
— оценивать усваиваемое содержание (исходя личностных ценностей);
— устанавливать связь между целью деятельности и ее результатом.
Регулятивные УУД:
— определять и формулировать цель деятельности на уроке;
— проговаривать последовательность действий на уроке; работать по плану, инструкции;
— высказывать свое предположение на основе учебного материала;
— отличать верно выполненное задание от неверного;
— осуществлять самоконтроль;
— совместно с учителем и одноклассниками давать оценку деятельности на уроке.
Познавательные УУД:
— ориентироваться в тетради;
— ориентироваться в своей системе знаний (определять границы знания/незнания);
— проводить анализ учебного материала;
— проводить сравнение, объясняя критерии сравнения.
Коммуникативные УУД:
— слушать и понимать речь других;
— умение с достаточной полнотой и точностью выражать свои мысли;
— владеть диалогической формой речи в соответствии с грамматическими и синтаксическими нормами родного языка.
Ход урока:
1.Самоопределение к деятельности
(Слайд 1)
Математика пришла,
Занимай свои места!
Математика сложна,
Но скажу с почтением:
Математика нужна
Всем без исключения.
2. Да, математика — наука сложная. Сегодня перед нами нелегкое испытание. А готовы ли мы к нему? Давайте проверим.
Проверка домашнего задания по карточкам. Взаимопроверка.
(Слайд 2,3)
3. «Открытие» детьми нового знания
Мозговой штурм.
-Послушайте высказывание: (Слайд 4)
Я в листочке, я в кристалле,
Я в живописи, архитектуре,
Я в геометрии, я в человеке.
Одним я нравлюсь, другие
Находят меня скучной.
Но все признают, что
Я – элемент красоты.
— О каком математическом понятии идет речь в этом высказывании?
— Сложно сделать вывод только на основе одного высказывания.
— Выполним задания в тетради.
— Откройте тетрадь, запишите число, классная работа.
Задача 1. Начертите квадрат со стороной 3 см и разделите его на 4 равные части разными способами.
Один обучающийся выполняет задание у доски.
Задача 2. Графический диктант: Отступите по 3 клеточки сверху и слева и поставьте точку. 1 клеточку вправо, 1-вверх, 1-вправо, 3-вниз, 1-влево, 1-вверх, 1 влево,1-вверх. Отступите 2 клеточки вправо и начертите зеркало. Постройте изображение в зеркале. Кто знает, какую картинку мы получили? -Симметричную.
— Догадались, какова тема урока? Симметрия.
— Так что же означает слово «симметрия»? Давайте обратимся к словарю и вспомним значение этого слова. Толковый словарь
(Слайд 5)
— Слово «симметрия» в переводе с греческого звучит как «гармония», означая красоту, соразмерность, пропорциональность, одинаковость в расположении частей.
— И так тема нашего урока (Слайд 6)
— А почему у меня тема написана с маленькой буквы? (Нет первого слова)
— Правильно, значит, тему урока мы сформулировали не до конца. Чтобы узнать тему полностью, продолжим нашу работу.
4. Постановка проблемы.
— У вас на столе лежит квадрат.
— Начертите в нем ось симметрии.
Знаете, как это сделать? (Нет) Почему? (Мы не знаем, что такое ось симметрии)
-Может теперь кто-то попробует сформулировать тему урока полностью?
(Осевая симметрия) (Слайд 7)
— Давайте выясним, что же такое ось симметрии и где же ее начертить.
— Сложим квадрат пополам и четко обозначим линию сгиба.
— Части квадрата одинаковые?
— Что мы получили? Покажите!
— Обведём цветным карандашом получившуюся прямую.
Это и есть ось симметрии.
Откройте учебник-тетрадь на с.52, прочитайте и выполните задание №2. (Рассмотрите рисунок)
Вывод: в каждом из рисунков мы нашли ось симметрии. Ось симметрии делит фигуру на одинаковые равные части. Если половинки не совпадают – это не ось симметрии и фигура не симметрична.
6.Первичное закрепление. Осознание, осмысление.
Практическая работа.
Цель: усвоение нового способа действий. Схематическое проведение оси симметрии фигур.
— Давайте попробуем сложить квадрат вновь пополам, но по-другому
— Что получили?
— Покажите!
— Как еще можно сложить квадрат?
— Так сколько же осей симметрии у квадрата? (4)
— Правильно!
— Сейчас проведем исследование, сколько осей симметрии имеют другие фигуры. Работать будем в группах.
— Давайте вспомним правила работы в группах.
(Слайд 
- Слышать и слушать друг друга
- Помогать друг другу
- Работать, соблюдая тишину
- Уметь договариваться
- Распределять обязанности
Достаньте и конверта фигуры и таблицу. Ваша задача определить, сколько осей имеет каждая фигура
и заполнить таблицу.
Конверт №1
- Работа с прямоугольником. (2)
- Работа с ромбом (2)
- Работа с кругом. (множество)
- Работа с равносторонним треугольником (3)
- Работа с прямоугольным треугольником.(нисколько)
Проверим. ( каждая группа называет по очереди фигуру из таблицы и количество осей.
(Слайд 9) Заполненная таблица
— Все ли фигуры имеют оси симметрии? (Нет)
|
Фигура |
Количество осей |
|
Прямоугольник |
2 |
|
Ромб |
2 |
|
Квадрат |
4 |
|
Круг |
~ |
|
Прямоугольный треугольник |
— |
|
Равносторонний треугольник |
3 |
Назовите самую «симметричную фигуру» (Круг).
Назовите самую «несимметричную фигуру» (Прямоугольный треугольник).
(Слайд 10)
Вывод: если фигура имеет оси симметрии- симметричная, нет – не симметричная
А сейчас немножко отдохнём. (Физминутка)
На доске (открыть зеленую доску) с одной стороны нарисованы фигуры, вы выбегая по очереди с каждой группы должны нарисовать симметричную фигуру справа и провести в ней ось.
7. Включение в систему знаний и повторение
— Мы выяснили, что симметрия в математике существует, но не у всех фигур. Только ли в этой науке она может быть?
— Оказывается, все в мире, и даже в нашей Галактике, построено по принципу симметрии. Древние греки считали, что Вселенная симметрична просто потому, что симметрия прекрасна.
— Симметрия – это красота, равновесие, гармония — Согласны?
— Давайте это докажем. Продолжим нашу исследовательскую работу.
8. Проектная деятельность.
— Каждой группе нужно провести исследование — в своей области. Доказать, или опровергнуть наличие симметричности и, конечно же, сделать выводы о проделанной работе.
— Каждая группа получает свой объект
-Возьмите в руки конверт №3. Вытащите предмет и задание.
1 группа. Симметрия в мире животных.
• На белой бумаге перед вами – контур бабочки. Проведите ось симметрии, раскрасьте бабочку в соответствии с правилами симметрии.
• Определить оси симметрии у данных животных.
2 группа. Симметрия в русском языке.
• Прочитать слова или фразы – палиндромы (читаемые слева направо и справа налево одинаково). Определить у них оси симметрии.
• Определить оси симметрии у данных букв русского языка
Дорисуй буквы в соответствии с правилами симметрии.
3 группа. Симметрия в мире растений.
• На белой бумаге перед вами – контур растения. Проведите ось симметрии, раскрасьте в соответствии с правилами симметрии.
• Определить оси симметрии у данных растений.
Выступление групп (Слайд 11,12,13,14 ) (Проверка)
Но симметрия может встречаться не только в указанных группах, но и в другой окружающей нас действительности.
9. Домашнее задание
(Слайд 15) Подготовить сообщение или презентацию о других областях окружающей нас действительности, где встречается симметрия
10. Рефлексия деятельности.
Работа за компьютером.
Тест «Симметрия» (работа с девайсами)
11.Вывод (Слайд 15)
12.Итог урока
— Завершим наш урок интервью.
Сегодня на уроке мне:
-было интересно …
-было трудно…
-больше всего понравились задания…
(Слайд 16)
— Вы собой довольны? Если да, похвалите себя: похлопайте себе в ладоши или погладьте по головке.
(Слайд 17)
Урок окончен. Всем спасибо!
Симметрия
Решить выражения
G
=80
118 — 38
=186
24+162
=40
80:16х8
=60
3х26 -18
=720
81:9х80
=8
=180
400х2:100
140:70х90
=30
=5
50х60:100
45: (13-4)
A
C
B
F
D
E
Симметрия
Симметрия — зеркальное отражение предметов, которые при наложении друг на друга полностью совпадают.
Слово «симметрия» (symmetria) происходит от греческого «сим» — с, вместе и «метрон» — мера, буквально означает соразмерность, одинаковость в расположении частей чего-либо относительно точки, прямой, плоскости.
В древности слово «симметрия» употреблялось для обозначения гармонии, красоты.
Симметрия — в широком или узком смысле в зависимости от того, как вы определите значение этого понятия, — является той идеей, посредством которой человек на протяжении веков пытался постичь и создать порядок, красоту и совершенство.
Г.Вейль
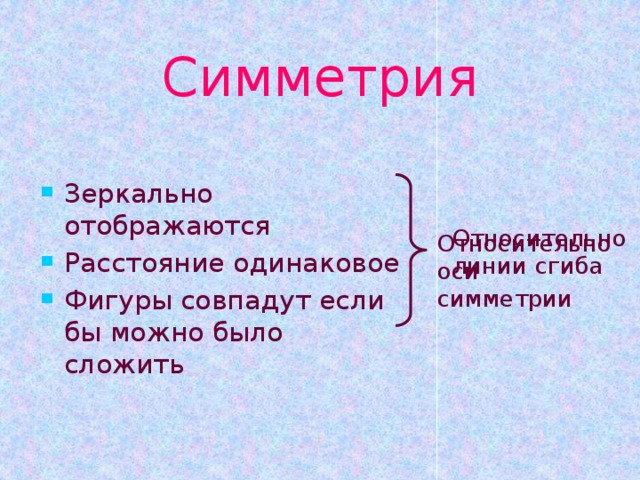
Симметрия
- Зеркально отображаются
- Расстояние одинаковое
- Фигуры совпадут если бы можно было сложить
Относительно линии сгиба
Относительно оси симметрии
Ось симметрии – прямая относительно которой расположены одинаковые части фигуры или сами фигуры.
Осевая симметрия – симметрия относительно какой-либо оси.
В природе
Озеро
Чуть колыша камыши,
Дремлет озеро в тиши.
Отраженья в нём живут:
Тучи в озере плывут,
Бор сосновый, как живой
Дремлет книзу головой.
Ю. Коринец
Животный и растительный мир
«Бабочка».
Ты прав. Одним воздушным очертаньем Я так мила. Весь бархат мой с его живым миганьем – Лишь два крыла.
А. А. Фет
В архитектуре
В технике
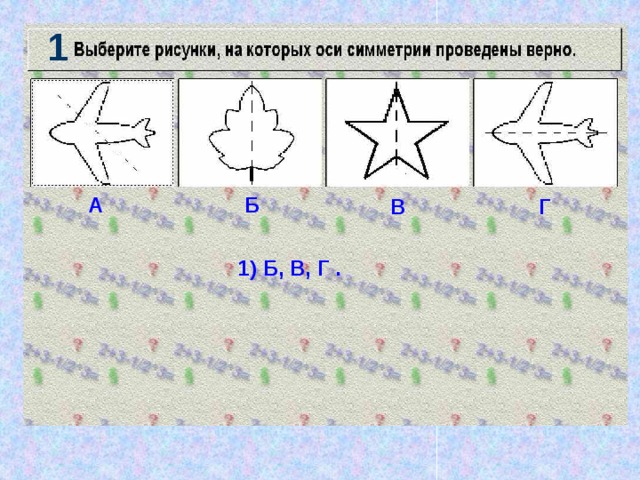
1
А
Б
В
Г
1) Б, В, Г .
2
А
Б
В
Г
3
А
Б
В
Г
4
А
Б
В
Г
Д
Е
5
А
Б
В
Г
Д
Е
6
А
Б
В
Г
Д
Е
7
А
Б
В
Г
Д
Е
8
А
Б
В
Г
Д
9
А
Б
В
Г
Д
Е
- 1) Б, В, Г.
- 2) А, В, Г.
- 3) Б, В, Г.
- 4) А, Г, Д.
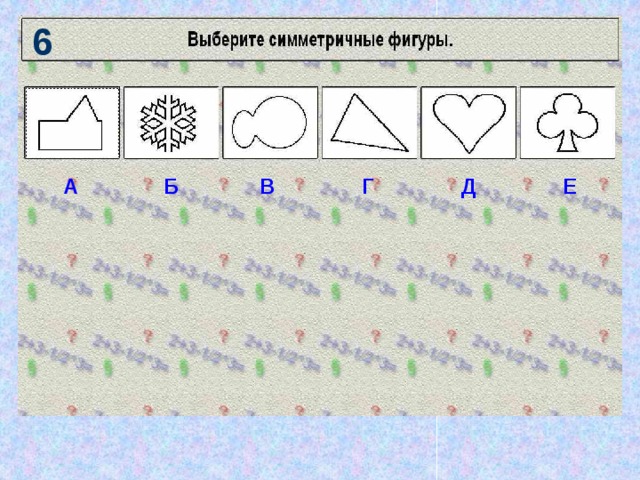
- 5) Б, Д, Е.
- 6) Б, Д, Е.
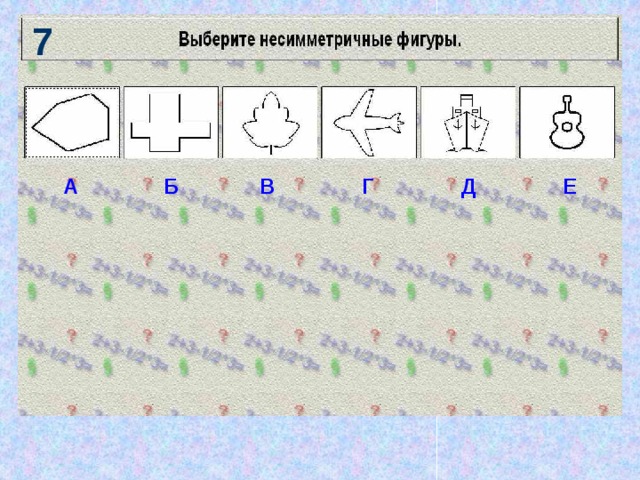
- 7) А,Б.
-
Д.
- 9) А, Д.
- Симметричные
- Ассиметричные
G
A
C
B
A
C
B
F
E
D
G
D
E
F
Задача 1
- 7 х 2 = 14 (см)
- (14 + 14) х 2 = 56 (см)
Задача 2
- 5 х 5 = 25 (см2)
- 25 х 2 = 50 (см2)
Симметрия — в широком или узком смысле в зависимости от того, как вы определите значение этого понятия, — является той идеей, посредством которой человек на протяжении веков пытался постичь и создать порядок, красоту и совершенство.
Г.Вейль.