Как найти ориентацию базиса

Координаты вектора в пространстве и базис

Базисом в пространстве называются три некомпланарных вектора , взятые в определённом порядке (рис.1.32). Эти векторы называются базисными.

Пусть в пространстве задан базис . Построим прямые , содержащие базисные векторы соответственно. Без ограничения общности можно считать, что эти прямые пересекаются в одной точке (в противном случае можно было взять любые пересекающиеся в одной точке прямые , параллельные прямым соответственно, поскольку проекции вектора на параллельные прямые равны. Тогда любой вектор можно однозначно представить в виде суммы своих проекций: , где — векторы, принадлежащие прямым соответственно (см. п.2 теоремы 1.1). Раскладывая проекции по базисам на соответствующих прямых (см. разд.1.3.1), находим: . Подставляя эти разложения в равенство , получаем

Таким образом, справедлива следующая теорема.

Теорема 1.5 (о разложении вектора по базису в пространстве). Любой вектор может быть разложен по базису в пространстве, т.е. представлен в виде (1.4), где числа определяются однозначно.

Коэффициенты в разложении (1.4) называются координатами вектора относительно базиса (число , называют абсциссой, — ординатой, а — аппликатой вектора ). Например, числа являются координатами вектора ( — абсцисса, — ордината, — аппликата вектора ).

Базисные векторы , отложенные от одной (произвольной) точки, называются репером.

Замечания 1.6

1. Базис на прямой, на плоскости, в пространстве определяется неоднозначно. Например, если — базис в пространстве, то система векторов при любом также является базисом.

2. Следующие свойства выражают геометрический смысл линейной зависимости и линейной независимости векторов:

а) два (и более) коллинеарных вектора линейно зависимы, и наоборот, два линейно зависимых вектора коллинеарны;

два линейно независимых вектора не коллинеарны;

б) три (и более) компланарных вектора линейно зависимы, и наоборот, три линейно зависимых вектора компланарны;

три линейно независимых вектора не компланарны;

в) четыре (и более) вектора линейно зависимы.

Докажем, например, последнее свойство. Пусть — произвольные векторы. Если первые три вектора линейно зависимы, то и вся система — линейно зависима. Если же векторы линейно независимы, то согласно пункту 2,»б» они не компланарны и, следовательно, образуют базис в пространстве. Тогда вектор можно разложить по этому базису, т.е. представить в виде линейной комбинации векторов . В этом случае система векторов также линейно зависима (см. свойство 4 в разд. 1.1.3).

3. Понятие базиса непосредственно связано с понятием линейной независимости. Базис представляет собой упорядоченную совокупность линейно независимых векторов:

а) на прямой — это один линейно независимый вектор (см. пункт 1 замечаний 1.2);

б) на плоскости — это два линейно независимых вектора на этой плоскости, взятые в определённом порядке (см. пункт 2,»а»);

в) в пространстве — это три линейно независимых вектора, взятые в определённом порядке (см. пункт 2,»б»).

4. Теоремы 1.3-1.5 позволяют говорить, что базис — это полная система векторов (на прямой, на плоскости, в пространстве) в том смысле, что любой вектор (на прямой, на плоскости, в пространстве) линейно выражается через базисные векторы.

5. Теоремы 1.3-1.5 позволяют говорить, что базис — это максимальная линейно независимая система векторов (на прямой, на плоскости, в пространстве), так как базис — это линейно независимая система векторов, и ее нельзя дополнить каким-либо вектором без потери линейной независимости.

6. Базис — это полная линейно независимая система векторов (на прямой, на плоскости, в пространстве).

Ориентации базисов в пространстве

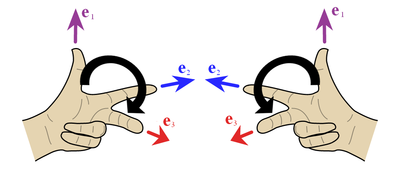
Базис в пространстве называется правым (или, что то же самое, упорядоченная тройка некомпланарных векторов называется правой тройкой), если, наблюдая из конца третьего вектора, кратчайший поворот от первого вектора ко второму виден происходящим против часовой стрелки (рис.1.33,а). Если описанный поворот виден происходящим по часовой стрелке, то базис называется левым (упорядоченная тройка некомпланарных векторов называется левой тройкой) (рис. 1.33,б).

Отметим следующие свойства: если тройка некомпланарных векторов — правая, то тройки, получающиеся «циклической» перестановкой трех векторов — также правые, а тройки, получающиеся перестановкой двух векторов или заменой одного вектора противоположным (например, — левые).

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Ориентация[править]

На прямой можно перемещаться в одном из двух противоположных направлений.
Ориентацией прямой называется выбор одного из них.
Аналогично можно говорить об ориентации отрезков прямой.

Пусть дано четыре точки на прямой.
Если ориентация направленных отрезков и совпадает, то они называются одноименными.
Фраза «ориентация совпадает» означает, что движение от к и от к происходит в одну сторону.

Таким образом, все векторы на прямой можно разделить на два класса.
Представители каждого из них ориентированны одинаково.
На прямой можно задать ориентацию, то есть выбрать какой из этих классов положителен, а какой отрицателен.
Те векторы, ориентация которых совпадает с заданной ориентацией прямой, называются положительно ориентированными; не совпадает — отрицательно ориентированными.

Если нарисовать ориентированную прямую, а затем перевернуть лист бумаги, очевидно, ориентация прямой поменяется на противоположную.

Понятие ориентации непосредственно не переносится на плоскость и пространство.

Упорядоченная тройка точек плоскости называется неколлинеарной тройкой, если эти точки не лежат на одной прямой.
Аналогично, упорядоченная четверка точек пространства называется некомпланарной четверкой, если эти точки не лежат в одной плоскости.
Если упорядоченная тройка точек плоскости неколлинеарна, очевидно, векторы и также неколлинеарны, а, значит, образуют базис на плоскости.
Аналогично, для некомпланарной четверки точек , векторы , и также некомпланарны, а, значит, образуют базис в пространстве.

Базис на плоскости называется право ориентированным, если кратчайший поворот от первого вектора базиса ко второму происходит против часовой стрелки, или лево ориентированным, если в обратную сторону.

§9. Ориентация базиса в пространстве.

  Рассмотрим произвольную тройку некомпланарных векторов.

Определение. Упорядоченная тройка некомпланарных векторов называется правой , если

а) кратчайший поворот от первого вектора ко второму, видимый из конца третьего происходит против часовой стрелки (т.е. в положительном направлении), или б) по правилу винта, или

в) по правилу правой руки. В противном случае − левой. И в том и в другом случае тройка называется ориентированной.

   Например, на рис.10 базис  { i,  j,  k } −  левый, а тройка  {a, b, c} на рис.11 – правая.

        с             Очевидно, что все одинаково ориентированные ортонормированные базисы могут

Вместе с этой лекцией читают «Пакеты прикладных программ».

           b          быть совмещены друг с другом с помощью параллельного переноса и поворота,

      a                а противоположно ориентированные − только с точностью до коллинеарности.

    Рис.11        Легко проверить, что тройки  a b c,  c a b  и  b c a  одинаково ориентированы, а

 тройки  a c b,  b a c  и  c b a   им противоположны. Т.е. круговая перестановка векторов не

меняет ориентацию, а не круговая – меняет.

Изменение знака у одного из векторов меняет ориентацию всей тройки.