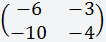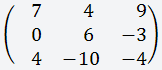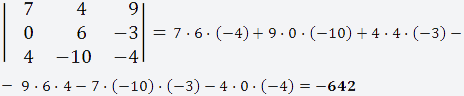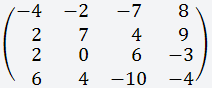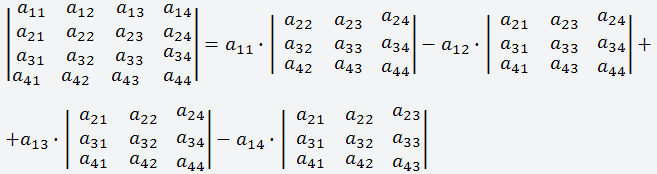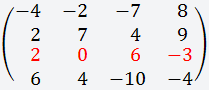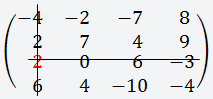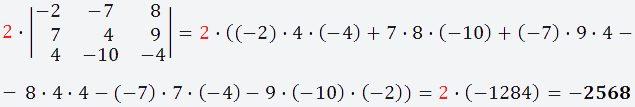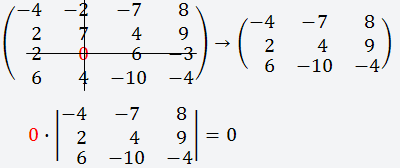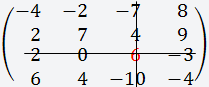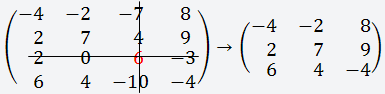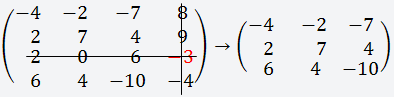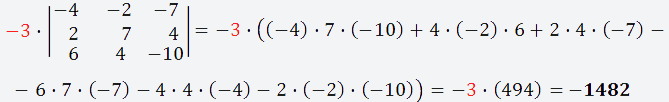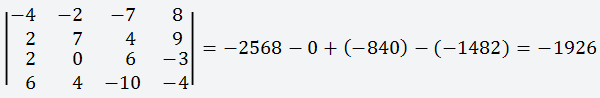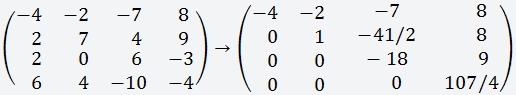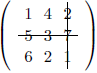Содержание
- Предупреждение
- Примеры вычисления определителя матрицы
- Определение
- Обозначения
- Свойства определителя
- Минор матрицы
- Алгебраическое дополнение элемента матрицы
- Порядок определителя
- Вычисление определителя матрицы
- Вычисление определителя матрицы 2×2
- Вычисление определителя матрицы 3×3
- Вычисление определителя матрицы 4×4
Пример вычисления определителя (детерминанта) матрицы
Определитель матрицы — является многочленом от элементов квадратной матрицы (если элементы матрицы это числа, тогда определитель матрицы тоже будет числом).
Для нахождения определителя матрицы, исходная матрица должна быть квадратной.
Дана матрица размером 2х2;
Что бы вычислить определитель матрицы 2х2 нужно из произведения элементов главной диагонали, вычесть произведение элементов побочной диагонали;
Дана матрица размером 3х3;
Что бы вычислить определитель матрицы 3х3 нужно воспользоваться формулой;
Подставляем наши значения в формулу;
Дана матрица размером 4х4;
Есть два способа вычисления определителя матрицы:
По определению — через разложение по строке или столбцу;
По методу Гаусса — приведение матрицы к треугольному виду (этот способ лучше использовать для решения матриц, размером 4х4 и более).
Решим пример первым способом (по определению — через разложение по строке или столбцу)
Чтобы вычислить определитель матрицы, нужно воспользоваться следующей формулой, в ней рассмотрен пример разложения матрицы по первой строке;
Выбираем строку или столбец (любую), лучше всего выбирать строку или столбец, где больше нулей, для удобства вычисления; В данном случае мы выбираем третью строку, так как в ней присутствует ноль;
Берём первый элемент этой строки (2); Теперь вычёркиваем третью строку и первый столбец;
Получаем матрицу 3х3;
Согласно формуле, мы умножаем выбранный нами элемент на определитель получившейся матрицы;
Вычисление определителя матрицы 3х3, мы рассматривали в примере №2
Далее делаем всё тоже самое, что и в шаге два, только берём второй элемент данной строки (0) и вычёркиваем третью строку и второй столбец;
Так как этот элемент равен нулю, то ни чего не нужно считать и так всё ясно;
Теперь берём третий элемент строки (6) и вычёркиваем третью строку и третий столбец;
Получаем матрицу 3х3;
Вычисляем определитель этой матрицы и умножаем на выбранный нами элемент (6)
Берём четвёртый элемент строки (-3) и вычёркиваем третью строку и четвёртый столбец;
Получаем матрицу 3х3;
Вычисляем определитель этой матрицы и умножаем на выбранный нами элемент (-3)
Чтобы вычислить определитель исходной матрицы, нужно сложить полученные результаты;
Опишем решение примера вторым способом (по методу Гаусса — приведение матрицы к треугольному виду)
Суть способа заключается в том, чтобы перед вычислением определителя, привести матрицу к треугольному виду. Если в ходе приведения матрицы к треугольному виду вы умножаете (делите) строку на число, то на это же число нужно будет умножить (разделить) полученный в конце определитель;
Пример приведения матрицы к треугольному виду мы уже рассматривали здесь
Итак, мы привили матрицу к треугольному виду;
Теперь чтобы вычислить определитель приведённой матрицы, нужно перемножить все элементы, стоящие на главной диагонали;
Данный онлайн калькулятор вычисляет определитель матрицы. Дается подробное решение. Для вычисления определителя матрицы выбирайте порядок (размер) квадратной матрицы. Введите данные в ячейки. Выберите метод решения и нажмите на кнопку «Вычислить». Теоретическую часть смотрите на странице определитель матрицы.
Предупреждение
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Примеры вычисления определителя матрицы
Пример 1. Найти определитель матрицы

Для вычисления определителя матрицы, приведем матрицу к верхнему треугольному виду.
Выбираем самый большой по модулю ведущий элемент столбца 1. Для этого меняем местами строки 1 и 2. При этом меняется знак определителя на «−»:

Исключим элементы 1-го столбца матрицы ниже главной диагонали. Для этого сложим строки 2,3 со строкой 1, умноженной на -1/78,-2/78 соответственно:
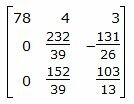
Исключим элементы 2-го столбца матрицы ниже главной диагонали. Для этого сложим строку 3 со строкой 2, умноженной на -5928/9048:

Мы привели матрицу к верхнему треугольному виду. Определитель матрицы равен произведению всех элементов главной диагонали (учитывая знак определителя):

Пример 2. Найти определитель матрицы A, разложением определителя по первой строке:

Для вычисления определителя матрицы методом разложения по первой строке, вычисляем произведение каждого элемента первой строки на соответствующее алгебраическое дополнение и суммируем полученные результаты:
Определение
Определитель (детерминант) квадратной матрицы A — это число, обладающее определенными свойствами, которое может быть получено из элементов матрицы рядом методов.
Обозначения
Пусть $ A = egin 1 & 4 & 2 5 & 3 & 7 6 & 2 & 1 end$
$det(A) = left|A
ight| = egin 1 & 4 & 2 5 & 3 & 7 6 & 2 & 1 end$
Свойства определителя
- Если матрица имеет строку или столбец, все элементы которого равны нулю, то ее определитель равен 0.
Пример 12
$egin 1 & 4 & 2 0 & 0 & 0 3 & 9 & 5 end= 0$ или $egin 1 & 4 & 0 4 & 2 & 0 3 & 9 & 0 end=0$
Если в матрице есть две одинаковых строки или два одинаковых столбца, то ее определитель равен 0.
Пример 13
$egin 1 & 4 & 2 1 & 4 & 2 3 & 9 & 5 end= 0$ или $egin 1 & 4 & 1 4 & 2 & 4 3 & 9 & 3 end=0$
Если в матрице есть две пропорциональных строки или два пропорциональных столбца, то ее определитель равен 0.
Пример 14
$egin 1 & 4 & 2 2 & 8 & 4 3 & 9 & 5 end= 0$ (две первые строки пропорциональны)
или
$egin 8 & 4 & 7 4 & 2 & 3 18 & 9 & 8 end=0$ (два первых столбца пропорциональны)
Если некоторая строка (столбец) является суммой или разностью других строк (столбцов), то определитель равен 0.
Пример 15
$egin 1 & 4 & 2 7 & 2 & 3 8 & 6 & 5 end= 0$ $R_ <1>+R_ <2>=R_<3>$ или
$ egin 9 & 12 & 3 1 & 8 & 7 5 & 7 & 2 end=0$ $C_<1>+C_<3>=C_<2>$
При вычислении определителя можно выносить общие множители целых строк или столбцов.
Пример 17
$egin 1 & 5 3 & 8 end$ $xlongequal<1>+R_<2>> egin 4 & 13 3 & 8 end$
Пример 18
$egin 1 & 5 3 & 8 end$ $xlongequal<1>+C_<2>> egin 6 & 5 11 & 8 end$
При вычислении определителя можно прибавлять или отнимать строки и столбцы, умноженные на произвольный коэффициент .
Пример 20
$egin 1 & 5 3 & 8 end$ $xlongequal<5C_<1>-C_<2>> egin 0 & 5 7 & 8 end$
Минор матрицы
Определитель матрицы, полученной вычеркиванием некоторых строк и столбцов матрицы, называется минором этой матрицы.
Пример 21
$A=egin 1 & 4 & 2 5 & 3 & 7 6 & 2 & 1 end$
Один из миноров матрицы A есть $egin 1 & 2 5 & 3 end$ (он получается вычеркиванием строки 3 и столбца 3 из матрицы A)
Другим минором является $egin 1 & 2 6 & 1 end$ (получается вычеркиванием строки 2 и столбца 2 из матрицы A)
Пример 22
$B=egin 2 & 5 & 1 & 3 4 & 1 & 7 & 9 6 & 8 & 3 & 2 7 & 8 & 1 & 4 end $
Один из миноров матрицы B есть $ egin 1 & 7 & 9 8 & 3 & 2 8 & 1 & 4 end$ (получается вычеркиванием строки 1 и столбца 1 из матрицы B)
Другим минором является $egin 1 & 7 8 & 3 end$ (получается вычеркиванием строк 1 и 4 и столбцов 1 и 4 из матрицы B)
Пусть $A= egin a_ <1,1>& a_ <1,2>& a_ <1,3>& . & . & a_<1,n> a_ <2,1>& a_ <2,2>& a_ <2,3>& . & . & a_<2,n> a_ <3,1>& a_ <3,2>& a_ <3,3>& . & . & a_<3,n> . & . & . & . & .& . a_ & a_ & a_ & . & . & a_ end$
Можно определить минор $Delta_$, полученный вычеркиванием строки i и столбца j, для любого элемента $a_$ квадратной матрицы A. Такой минор называется дополнительным.
Определить дополнительный минор элемента 2. Так как данный элемент находится в строке 2, столбце 1, видно, что это $a_<2,1>$.
Нужно вычеркнуть строку 2 и столбец 1 из матрицы A, после чего получаем
Минор, дополнительный к элементу 2, есть $Delta_ <2,1>= 7$.
Пример 24
$B=egin 1 & 4 & 2 5 & 3 & 7 6 & 2 & 1 end$
Нужно найти минор, дополнительный к элементу 7. Так как данный элемент находится в строке 2, столбце 3, видно, что это $a_<2,3>$.
Мы должны вычеркнуть строку 2 и столбец 3 из матрицы B, после чего мы получаем
Минор, дополнительный к элементу 7, — это $Delta_<2,3>= egin 1 & 4 6 & 2 end$
Пример 25
$C=egin 2 & 5 & 1 & 3 4 & 1 & 7 & 9 6 & 8 & 3 & 2 7 & 8 & 1 & 4 end$
Нужно найти минор, дополнительный к элементу 5. Так как данный элемент находится в строке 1, столбце 2, видно, что это $a_<1,2>$.
Мы должны вычеркнуть строку 1 и столбец 2 из матрицы C, после чего мы получаем
Минор, дополнительный к элементу 5, — это $Delta_<1,2>= egin 4 & 7 & 9 6 & 3 & 2 7 & 1 & 4 end$
Алгебраическое дополнение элемента матрицы
Каждому элементу $a_$ матрицы A соответствует алгебраическое дополнение $(-1)^cdotDelta_$. Например, алгебраическое дополнение $(-1)^<2+5>cdotDelta_<2,5>=(-1)^<7>cdotDelta_<2,5>= -Delta_ <2,5>$ соответствует элементу $a_<2,5>$.
Порядок определителя
Порядок определителя матрицы равен числу ее строк и столбцов.
Пример 26
$egin 1 & 4 6 & 2 end$ (матрица имеет 2 строки и 2 столбца, так что порядок определителя равен 2)
Пример 27
$egin 4 & 7 & 9 6 & 3 & 2 7 & 1 & 4 end$ (матрица имеет 3 строки и 3 столбца, так что порядок определителя равен 3)
Вычисление определителя матрицы
Определитель матрицы равен сумме произведений элементов любой строки или любого столбца и их алгебраических дополнений.
$left| A
ight| = egin a_ <1,1>& a_ <1,2>& a_ <1,3>& . & . & a_<1,n> a_ <2,1>& a_ <2,2>& a_ <2,3>& . & . & a_<2,n> a_ <3,1>& a_ <3,2>& a_ <3,3>& . & . & a_<3,n> . & . & . & . & .& . a_ & a_ & a_ & . & . & a_ end$
Можно посчитать определитель, например, используя строку i:
Либо же можно посчитать определитель, используя столбец j:
Вычисление определителя матрицы 2×2
Используем строку 1, чтобы вычислить определитель.
Заметим, что $ Delta_<1,1>= a_ <2,2>$ и $ Delta_<1,2>=a_<2,1>$
$ left| A
ight| =a_ <1.1>cdot a_<2,2>- a_ <1.2>cdot a_<2,1>$
$color < egina & b c & d end =a cdot d — b cdot c>$
Пример 28
$egin 2 & 5 3 & 8 end =2 cdot 8 — 3 cdot 5 = 16 -15 =1$
Пример 29
$egin -4 & 7 -2 & 9 end =-4 cdot 9 — 7 cdot (-2) = -36 -(-14) =-36 + 14 = — 22$
Вычисление определителя матрицы 3×3
Используем строку 1, чтобы вычислить определитель.
Упростить получение последней формулы можно следующим образом.
Начнем с того, что перепишем первые две строки под определителем как показано ниже.
Умножаем элементы на каждой из трех красных диагоналей (на главной диагонали и на диагоналях под ней) и складываем результаты:
$colorcdot a_<2,2>cdot a_<3,3>+ a_<2,1>cdot a_<3,2>cdot a_<1,3>+a_<3,1>cdot a_<1,2>cdot a_<2,3>>$
Умножаем элементы на каждой из трех синих диагоналей (на побочной диагонали и на диагоналях под ней) и складываем результаты:
Вычитая вторую сумму из первой, получаем формулу определителя:
Пример 30
$A=egin 1 & 4 & 3 2 & 1 & 5 3 & 2 & 1 end$
Пример 31
$A=egin 3 & 5 & 1 1 & 4 & 2 7 & 1 & 9 end$
$= 3cdot4cdot9 + 1cdot1cdot1 + 7cdot5cdot2 -(1cdot4cdot7 + 2cdot1cdot3 + 9cdot5cdot1) =$ $ 108 + 1 + 70 -(28 + 6 + 45)=79-79=100$
Элементы матрицы могут быть обозначены буквами. Вычисление их определителей можно упростить, используя свойства определителей. Например, можно вычислить определитель матрицы, в которой к какой-либо строке (или столбцу) прибавлена линейные комбинация других строк (столбцов).
$egin a & b & c c & a & b b & c & a end$ $ xlongequal<1>+C_<2>+C_<3>> egin a + b + c & b & c c + a + b & a & b b + c + a & c & a end = (a + b + c) cdot egin 1 & b & c 1 & a & b 1 & c & a end$
Вычисляем последней определитель:
$ = a^ <2>+ b^ <2>+ c^ <2>-acdot c — bcdot c — acdot b =$ $frac<1><2>cdot(2a^ <2>+2b^<2>+2c^ <2>-2acdot b -2acdot c-2bcdot c) =$ $frac<1><2>cdot(a^<2>-2acdot b + b^<2>+ a^<2>-2acdot c +c^<2>+b^<2>-2bcdot c + c^<2>)=$ $frac<1><2>cdot[(a-b)^<2>+(a-c)^<2>+(b-c)^<2>]$
В итоге получаем:
Пример 32
Вычислим определитель матрицы Вандермонде.
$egin 1 & 1 & 1 a & b & c a^ <2>& b^ <2>& c^ <2>end$
Используя свойства определителей, модифицируем строку 1 так, чтобы два элемента обратились в 0. В этом случае, когда мы используем полученную выше формулу для определителя матрицы 3×3, нет необходимости вычислять алгебраические дополнения этих элементов, поскольку их произведение будет равно 0.
Вычисление определителя матрицы 4×4
Вычислить определитель матрицы 4×4 можно с использованием общей формулы для определителя матрицы 3×3.
Но сначала надо использовать свойства определителей:
- Проверим, не выполняется ли одно из условий того, что определитель равен 0.
- Проверим, нельзя ли вынести общий множитель из одной или нескольких строк или столбцов.
- Проверим, не является ли данная матрица матрицей Вандермонде, возможно, такой, в которой некоторые строки или столбцы переставлены.
В любом из этих случаев нам пригодятся соответствующие методы вычисления определителей матриц 3×3. Модифицируем строку или столбец так, чтобы все его элементы, кроме одного, обратились в 0. Определитель будет равен произведению этого ненулевого элемента на его алгебраическое дополнение. В этом случае, алгебраическое дополнение — это определитель матрицы 3×3, который считается по уже известной формуле.
Пример 33
$egin 1 & 3 & 9 & 2 5 & 8 & 4 & 3 0 & 0 & 0 & 0 2 & 3 & 1 & 8 end$
Замечаем, что все элементы в строке 3 равны нулю, а значит, определитель равен 0.
Пример 34
$egin 1 & 3 & 1 & 2 5 & 8 & 5 & 3 0 & 4 & 0 & 0 2 & 3 & 2 & 8 end$
Замечаем, что $C_<1>$ равно $C_<3>$, следовательно, определитель равен 0.
Пример 35
$egin 1 & 3 & 9 & 2 5 & 8 & 4 & 3 10 & 16 & 18 & 4 2 & 3 & 1 & 8 end$
Замечаем, что строки 2 и 3 пропорциональны друг другу, следовательно, определитель равен 0.
Пример 36
$egin color <4>& 3 & 2 & 2 0 & 1 & -3 & 3 0 & -1 & 3 & 3 0 & 3 & 1 & 1 end$
Поскольку в столбце 1 только один элемент отличен от нуля, применяем общую формулу, используя этот столбец. Алгебраические дополнения нулевых элементов считать не надо, так как их произведения на эти элементы все равно будут равны нулю.

$=4(1cdot3cdot1 +(-1)cdot1cdot3+3cdot(-3)cdot3$ $-(3cdot3cdot3+3cdot1cdot1 +1cdot(-3)cdot(-1)))$ $=4(3-3-27-(27+3+3))=4cdot(-60)=-240$
Пример 37
$egin 4 & 3 & 2 & 2 0 & 1 & 0 & -2 1 & -1 & 3 & 3 2 & 3 & 1 & 1 end$
Чтобы изменить строку так, чтобы в ней стало больше нулей, нужно совершать операции со столбцами, и наоборот. Выбираем строку или столбец, содержащий элемент 1, поскольку из него можно получить любое число простым умножением.
Заметим, что в строке 2 уже есть два нулевых элемента. Достаточно обратить лишь еще один элемент в 0, чтобы осталось посчитать только одно алгебраическое дополнение единичного элемента.
$egin 4 & 3 & 2 & 2 0 & 1 & 0 & -2 1 & -1 & 3 & 3 2 & 3 & 1 & 1 end xlongequal<4>+2C_<2>>$ $egin 4 & 3 & 2 & 8 0 & color <1>& 0 & 0 1 & -1 & 3 & 1 2 & 3 & 1 & 7 end=$ 
$= 1cdot(-1)^<2+2>cdot egin 4 & 2 & 8 1 & 3 & 1 2 & 1 & 7 end=$
$=4cdot3cdot7 + 1cdot1cdot8 + 2cdot2cdot1$ $-(8cdot3cdot2 + 1cdot1cdot4 + 7cdot2cdot1) =$ $ 84 + 8 + 4- 48-4-14=30$
Пример 38
$egin 1 & -2 & 3 & 2 2 & 3 & 1 & -1 3 & 3 & 3 & 3 -1 & 4 & 2 & 1 end$
Можно вынести множитель 3 из строки 3:
$3cdot egin 1 & -2 & 3 & 2 2 & 3 & 1 & -1 1 & 1 & 1 & 1 -1 & 4 & 2 & 1 end$
Поскольку в строке 3 все элементы равны 1, легко обратить получить нули.
$egin 1 & -2 & 3 & 2 2 & 3 & 1 & -1 1 & 1 & 1 & 1 -1 & 4 & 2 & 1 end$ $ xlongequal <1>— C_<4>,C_<2>-C_<4>,C_<3>-C_<4>> egin -1 & -4 & 1 & 2 3 & 4 & 2 & -1 0 & 0 & 0 & color<1> -2 & 3 & 1 & 1 end$ $=1cdot(-1)^<3+4>cdot$ 
$=-((-1)cdot 4cdot 1 +3 cdot 3cdot1 + (-2)cdot (-4)cdot 2$ $- (1cdot 4cdot (-2) + 2cdot 3cdot (-1) + 1cdot (-4)cdot3))$ $=-(-4 + 9 + 16 + 8 + 6 + 12) =-47$
Пример 39
$egin 2 & 5 & 1 & 4 4 & 1 & 6 & 3 5 & 3 & 7 & 2 1 & 0 & 2 & 4 end$
Здесь мы можем использовать единицу из последней строки и обратить остальные элементы первого столбца в нули.
$egin 2 & 5 & 1 & 4 4 & 1 & 6 & 3 5 & 3 & 7 & 2 1 & 0 & 2 & 4 end$ $xlongequal<1>-2R_<4>,R_<2>-4R_<4>, R_<3>-5R_<4>> egin 0 & 5 & -3 & -4 0 & 1 & -2 & -13 0 & 3 & -3 & -18 color <1>& 0 & 2 & 4 end=$ 
Выносим общий множитель -1 из столбца 2 и еще раз -1 из столбца 3.
$ (-1)cdot(-1)cdot(-1)cdot egin 5 & 3 & 4 1 & 2 & 13 3 & 3 & 18 end=$ $(-1)cdot egin 5 & 3 & 4 1 & 2 & 13 3 & 3 & 18 end=$ $-[5cdot 2cdot 18 + 1cdot 3cdot 4+ 3cdot 3cdot 13 — (4cdot 2cdot 3cdot + 13cdot 3cdot 5 + 18cdot 3cdot 1)]=$ $-(180+12+117-24-195-54)=36$
Пример 40
$egin 4 & 7 & 2 & 3 1 & 3 & 1 & 2 2 & 5 & 3 & 4 1 & 4 & 2 & 3 end$
Мы видим элемент 1 в столбце 3, так что мы можем обратить остальные элементы строки 2 в нули.
$egin 4 & 7 & 2 & 3 1 & 3 & 1 & 2 2 & 5 & 3 & 4 1 & 4 & 2 & 3 end$ $xlongequal<1>-C_<3>, C_<2>-3C_<3>,C_<4>-2C_<3>> egin 2 & 1 & 2 & -1 0 & 0 & color <1>& 0 -1 & -4 & 3 & -2 -1 & -2 & 2 & -1 end=$ 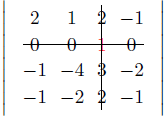
Выносим общий множитель -1 из строки 2 и еще раз -1 из строки 3.
$ (-1)cdot(-1)cdot(-1)cdot egin 2 & 1 & -1 1 & 4 & 2 1 & 2 & 1 end=$ $(-1)cdot egin 2 & 1 & -1 1 & 4 & 2 1 & 2 & 1 end=$ $-[2cdot 4cdot 1 + 1cdot 2cdot (-1)+ 1cdot 1cdot 2 — ((-1)cdot 4cdot 1 + 2cdot 2cdot 2 + 1cdot 1cdot 1)]=$ $-(8-2+2+4-8-1)=-3$
Пример 41
$egin 2 & 1 & 3 & 4 1 & 3 & 4 & 2 3 & 4 & 2 & 1 4 & 2 & 1 & 3 end$
Заметим, что все строки и все столбцы состоят из одних и тех же элементов, но в разном порядке. В таком случае мы можем сложить все строки или все столбцы.
$egin 2 & 1 & 3 & 4 1 & 3 & 4 & 2 3 & 4 & 2 & 1 4 & 2 & 1 & 3 end$ $xlongequal<1>+L_<2>+L_<3>+L_<4>> egin 10 & 10 & 10 & 10 1 & 3 & 4 & 2 3 & 4 & 2 & 1 4 & 2 & 1 & 3 end =$ $10cdot egin 1 & 1 & 1 & 1 1 & 3 & 4 & 2 3 & 4 & 2 & 1 4 & 2 & 1 & 3 end$ $xlongequal <1>— C_<4>,C_<2>-C_<4>,C_<3>-C_<4>>10cdot egin 0 & 0 & 0 & color<1> -1 & 1 & 2 & 2 2 & 3 & 1 & 1 1 & -1 & -2 & 3 end=$
$=10cdot1cdot(-1)^<1+4>$
$ = (-10)cdot egin -1 & 1 & 2 2 & 3 & 1 1 & -1 & -2 end=$ $(-10)cdot((-1)cdot 3cdot (-2) +2 cdot (-1)cdot2 + 1cdot 1cdot 1$ $-(2cdot 3cdot 1 + 1cdot (-1)cdot (-1) + (-2)cdot1cdot2))$ $= -10cdot(6 -4 +1 -6 — 1 + 4) =0$
Евгений Николаевич Беляев
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Есть несколько основных используемых способов для вычисления матричных определителей размерности 4×4. Первый из них — это приведение матрицы к ступенчатой форме посредством разрешённых преобразований, а второй — это разложение матрицы по строчке или столбцу.
Способ Гаусса
Способ разрешённых преобразований для нахождения определителей 4х4 интуитивно довольно прост и понятен: нужно преобразовать матричную таблицу так, чтобы снизу под главной диагональю стояли только нули, а после этого найти произведение элементов с этой самой диагонали. В процессе можно пользоваться свойствами определителей.
Свойства детерминанта
Также в процессе нахождения детерминанта можно пользоваться свойствами определителя, вот самые полезные из них:
- Определитель будет равен нулю, если какие-либо его строчки или столбцы полностью нулевые или пропорциональны между собой (то есть отличаются лишь каким-либо множителем);
- Общий множитель, присутствующий у всех элементов строчки или столбца, можно вынести за скобки и тем самым упростить процесс вычисления;
- При перестановке строчек или столбцов знак конечного вычисленного значения меняется на противоположный.
Сдай на права пока
учишься в ВУЗе
Вся теория в удобном приложении. Выбери инструктора и начни заниматься!
Получить скидку 3 000 ₽
Разложение по строчке
Тут нужно записывать определитель через сумму алгебраических дополнений элемента строчки или столбца, по которой производится разложение.
Алгебраическое дополнение одного элемента $a_ij$ вычисляется по формуле:
$(-1)^{i+j} cdot Δ_{ij}$, здесь $Δ_{ij}$ — минор элемента, он определяется путём вычёркивания строчки и столбца, в которой стоит рассматриваемый элемент.
Единица в степени $i+j$ по сути нужна для определения знака перед соответствующим минором, поэтому для простоты можно просто принять, что знаки чередуются в шахматном порядке, причём для элемента 1-ой строчки 1-ого столбца знак будет положительный.
Пример 1
Найдите определитель для $A$:
$A=begin{pmatrix} 1 & 2 & 3 & 4 \ 5 & 6 & 7 & 8 \ 9 & -9 & 9 & 0 \ 0 & 0 & 0 & 0 \ end{pmatrix}$
Решение:
Здесь всё просто, в строчке четыре стоят только нули, а это значит, что $Δ = 0$.
Пример 2
Посчитайте определитель для $B$:
$B=begin{pmatrix} 1 & 0 & -1 & -5 \ 1 & 6 & 4 & -5 \ 1 & 2 & -2 & -5 \ 1 & 3 & 0 & -5 \ end{pmatrix}$
Первый столбец отличается от последнего лишь множителем для всей строки, равным $-5$, а это значит, что здесь, как и в первом примере $Δ = 0$.
«Нахождение определителя матрицы 4 на 4» 👇
Пример 3
Дана матрица $C$. Найдите детерминант методом Гаусса:
$C = begin{pmatrix} 1 & 1 & 1 & -1 \ 1 & -2 & 1 & -1 \ 1 & 1 & 3 & 1 \ 1 & 1 & 1 & -4 \ end{pmatrix}$
Решение:
Ищем детерминант посредством составления треугольной матрицы. Для этого осуществляем следующие преобразования, для удобства обозначения осуществляемых со строками арифметических операций будем обозначать строчку как (n):
(4) — (1); (3) — (1); (2) — (1):
$begin{pmatrix} 1 & 1 & 1 & -1 \ 0 & -3 & 0 & 0 \ 0 & 0 & 2 & 0 \ 0 & 0 & 0 & -5 \ end{pmatrix}$
Теперь можно найти произведение с главной диагонали:
$Δ = 1 cdot (-3) cdot 2 cdot (-5) = 30$.
Пример 4
Проверьте себя и найдите определитель матричной таблицы $C$ разложением по строчке.
Решение:
Нулевых элементов в строчках и столбцах нет, поэтому разложим определитель по первой строчке, так как она имеет минимальные по модулю элементы. Знаки при каждом произведении запишутся в следующем порядке: $(+;-;+;-)$.
$begin{array} {|cccc|}1 & 1 & 1 & -1 \ 1 & -2 & 1 & -1 \ 1 & 1 & 3 & 1 \ 1 & 1 & 1 & -4 \ end{array}= 1 cdot begin{array} {|ccc|} -2 & 1 & -1 \ 1 & 3 & 1 \ 1 & 1 & -4 \ end{array} – 1 cdot begin{array} {|ccc|} 1 & 1 & 1 \ 1 & 3 & 1 \ 1 & 1 & -4 \ end{array} + 1 cdot begin{array} {|ccc|} 1 & -2 & 1 \ 1 & 1 & 1 \ 1 & 1 & -4 \ end{array} — begin{array} {|ccc|} 1 & -2 & 1 \ 1 & 1 & 3 \ 1 & 1 & 1 \ end{array} $
Теперь вычислим каждый минор по отдельности, воспользуемся правилом Саррюса:
$begin{array} {|ccc|} -2 & 1 & -1 \ 1 & 3 & 1 \ 1 & 1 & -4 \ end{array}= ( — 2) cdot 3 cdot ( — 4) + 1 cdot 1 cdot 1 + 1 cdot 1 cdot 1 – 1cdot 1 cdot (-4) — ( -2 ) cdot 1 cdot 1 — 1 cdot 3 cdot 1 = 24 + 1 + 1 + 4 + 2 – 3 = 29$;
$begin{array} {|ccc|} 1 & 1 & 1 \ 1 & 3 & 1 \ 1 & 1 & -4 \ end{array} = 1 cdot 3 ( — 4) + 1 cdot 1 cdot 1 + 1 cdot 1 cdot 1 – 1 cdot 1 cdot ( — 4) — 1 cdot 1 cdot 1 – 1 cdot 3 cdot 1 = -10$;
$begin{array} {|ccc|} 1 & -2 & 1 \ 1 & 1 & 1 \ 1 & 1 & 4 \ end{array} = 1 cdot 1 cdot ( — 4) + ( — 2) cdot 1 cdot 1 + 1 cdot 1 cdot 1 — ( — 2) cdot 1 cdot ( — 4) — 1 cdot 1 cdot 1 — 1 cdot 1 cdot 1 = -15$;
$begin{array} {|ccc|} 1 & -2 & 1 \ 1 & 1 & 3 \ 1 & 1 & 1 \ end{array} = 1 cdot 1 cdot 1 + ( — 2) cdot 3 cdot 1 + 1 cdot 1 cdot 1 — ( — 2) cdot 1 cdot 1 — 1 cdot 3 cdot 1 — 1 cdot 1 cdot 1 = 1 + ( — 6) + 1 + 2 – 3 – 1 = — 6$;
$Δ = 29 + 10 – 15 + 6 = 30$.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Каждой квадратной матрице ставится в соответствие некоторое число называемое определителем матрицы.
Существуют правила, которые позволяют вычислять определители матриц.
Объяснить вычисление Вашего определителя матрицы – основная цель создания данного калькулятора.
Алгоритм калькулятора умеет использовать элементарные преобразования определителя.
Их применение позволяет упростить вычисление определителей, правда, это возможно только для простых задач.
Пожалуйста, введите целые числа от -20 до 20 ( желательно от -10 до 10 ).
Содержание:
- Вычисления определителей второго порядка
- Методы вычисления определителей третьего порядка
- Приведение определителя к треугольному виду
- Правило треугольника
- Правило Саррюса
- Разложение определителя по строке или столбцу
- Разложение определителя по элементам строки или столбца
- Теорема Лапласа
В общем случае правило вычисления определителей
$n$-го порядка
является довольно громоздким. Для определителей второго и третьего порядка существуют рациональные способы их вычислений.
Вычисления определителей второго порядка
Чтобы вычислить определитель матрицы 
элементов главной диагонали отнять произведение
элементов побочной диагонали:
$$left| begin{array}{ll}{a_{11}} & {a_{12}} \ {a_{21}} & {a_{22}}end{array}right|=a_{11} cdot a_{22}-a_{12} cdot a_{21}$$
Пример
Задание. Вычислить определитель второго порядка
$left| begin{array}{rr}{11} & {-2} \ {7} & {5}end{array}right|$
Решение. $left| begin{array}{rr}{11} & {-2} \ {7} & {5}end{array}right|=11 cdot 5-(-2) cdot 7=55+14=69$
Ответ. $left| begin{array}{rr}{11} & {-2} \ {7} & {5}end{array}right|=69$
Методы вычисления определителей третьего порядка
Для вычисления определителей третьего порядка существует такие правила.
Правило треугольника
Схематически это правило можно изобразить следующим образом:
Произведение элементов в первом определителе, которые соединены прямыми,
берется со знаком «плюс»; аналогично, для второго определителя — соответствующие произведения берутся со знаком «минус», т.е.
$$left| begin{array}{ccc}{a_{11}} & {a_{12}} & {a_{13}} \ {a_{21}} & {a_{22}} & {a_{23}} \ {a_{31}} & {a_{32}} & {a_{33}}end{array}right|=a_{11} a_{22} a_{33}+a_{12} a_{23} a_{31}+a_{13} a_{21} a_{32}-$$
$$-a_{11} a_{23} a_{32}-a_{12} a_{21} a_{33}-a_{13} a_{22} a_{31}$$

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Вычислить определитель $left| begin{array}{rrr}{3} & {3} & {-1} \ {4} & {1} & {3} \ {1} & {-2} & {-2}end{array}right|$ методом треугольников.
Решение. $left| begin{array}{rrr}{3} & {3} & {-1} \ {4} & {1} & {3} \ {1} & {-2} & {-2}end{array}right|=3 cdot 1 cdot(-2)+4 cdot(-2) cdot(-1)+$
$$+3 cdot 3 cdot 1-(-1) cdot 1 cdot 1-3 cdot(-2) cdot 3-4 cdot 3 cdot(-2)=54$$
Ответ. $left| begin{array}{rrr}{3} & {3} & {-1} \ {4} & {1} & {3} \ {1} & {-2} & {-2}end{array}right|=54$
Правило Саррюса
Справа от определителя дописывают первых два столбца и произведения элементов на главной диагонали и на диагоналях, ей
параллельных, берут со знаком «плюс»; а произведения элементов побочной диагонали и диагоналей, ей параллельных,
со знаком «минус»:
$$-a_{13} a_{22} a_{31}-a_{11} a_{23} a_{32}-a_{12} a_{21} a_{33}$$
Пример
Задание. Вычислить определитель $left| begin{array}{rrr}{3} & {3} & {-1} \ {4} & {1} & {3} \ {1} & {-2} & {-2}end{array}right|$ с помощью правила Саррюса.
Решение.
$$+(-1) cdot 4 cdot(-2)-(-1) cdot 1 cdot 1-3 cdot 3 cdot(-2)-3 cdot 4 cdot(-2)=54$$
Ответ. $left| begin{array}{rrr}{3} & {3} & {-1} \ {4} & {1} & {3} \ {1} & {-2} & {-2}end{array}right|=54$
Разложение определителя по строке или столбцу
Определитель равен сумме произведений элементов строки определителя на их
алгебраические дополнения. Обычно выбирают
ту строку/столбец, в которой/ом есть нули. Строку или столбец, по которой/ому ведется разложение, будет обозначать стрелкой.
Пример
Задание. Разложив по первой строке, вычислить определитель $left| begin{array}{lll}{1} & {2} & {3} \ {4} & {5} & {6} \ {7} & {8} & {9}end{array}right|$
Решение. $left| begin{array}{lll}{1} & {2} & {3} \ {4} & {5} & {6} \ {7} & {8} & {9}end{array}right| leftarrow=a_{11} cdot A_{11}+a_{12} cdot A_{12}+a_{13} cdot A_{13}=$
$1 cdot(-1)^{1+1} cdot left| begin{array}{cc}{5} & {6} \ {8} & {9}end{array}right|+2 cdot(-1)^{1+2} cdot left| begin{array}{cc}{4} & {6} \ {7} & {9}end{array}right|+3 cdot(-1)^{1+3} cdot left| begin{array}{cc}{4} & {5} \ {7} & {8}end{array}right|=-3+12-9=0$
Ответ. $left| begin{array}{lll}{1} & {2} & {3} \ {4} & {5} & {6} \ {7} & {8} & {9}end{array}right|=0$
Этот метод позволяет вычисление определителя свести к вычислению определителя более низкого порядка.
Пример
Задание. Вычислить определитель $left| begin{array}{lll}{1} & {2} & {3} \ {4} & {5} & {6} \ {7} & {8} & {9}end{array}right|$
Решение. Выполним следующие
преобразования над строками определителя: из второй строки отнимем четыре
первых, а из третьей первую строку, умноженную на семь, в результате, согласно свойствам определителя, получим определитель,
равный данному.
$$left| begin{array}{ccc}{1} & {2} & {3} \ {4} & {5} & {6} \ {7} & {8} & {9}end{array}right|=left| begin{array}{ccc}{1} & {2} & {3} \ {4-4 cdot 1} & {5-4 cdot 2} & {6-4 cdot 3} \ {7-7 cdot 1} & {8-7 cdot 2} & {9-7 cdot 3}end{array}right|=$$
$$=left| begin{array}{rrr}{1} & {2} & {3} \ {0} & {-3} & {-6} \ {0} & {-6} & {-12}end{array}right|=left| begin{array}{ccc}{1} & {2} & {3} \ {0} & {-3} & {-6} \ {0} & {2 cdot(-3)} & {2 cdot(-6)}end{array}right|=0$$
Определитель равен нулю, так как вторая и третья строки являются пропорциональными.
Ответ. $left| begin{array}{lll}{1} & {2} & {3} \ {4} & {5} & {6} \ {7} & {8} & {9}end{array}right|=0$
Для вычисления определителей четвертого порядка и выше применяется либо разложение по строке/столбцу, либо приведение
к треугольному виду, либо с помощью теоремы Лапласа.
Разложение определителя по элементам строки или столбца
Пример
Задание. Вычислить определитель
$left| begin{array}{llll}{9} & {8} & {7} & {6} \ {5} & {4} & {3} & {2} \ {1} & {0} & {1} & {2} \ {3} & {4} & {5} & {6}end{array}right|$ , разложив его по элементам какой-то строки или какого-то столбца.
Решение. Предварительно выполним
элементарные преобразования над строками определителя, сделав
как можно больше нулей либо в строке, либо в столбце. Для этого вначале от первой строки отнимем девять третьих,
от второй — пять третьих и от четвертой — три третьих строки, получаем:
$$left| begin{array}{cccc}{9} & {8} & {7} & {6} \ {5} & {4} & {3} & {2} \ {1} & {0} & {1} & {2} \ {3} & {4} & {5} & {6}end{array}right|=left| begin{array}{cccc}{9-1} & {8-0} & {7-9} & {6-18} \ {5-5} & {4-0} & {3-5} & {2-10} \ {1} & {0} & {1} & {2} \ {0} & {4} & {2} & {0}end{array}right|=left| begin{array}{rrrr}{0} & {8} & {-2} & {-12} \ {0} & {4} & {-2} & {-8} \ {1} & {0} & {1} & {2} \ {0} & {4} & {2} & {0}end{array}right|$$
Полученный определитель разложим по элементам первого столбца:
$$left| begin{array}{rrrr}{0} & {8} & {-2} & {-12} \ {0} & {4} & {-2} & {-8} \ {1} & {0} & {1} & {2} \ {0} & {4} & {2} & {0}end{array}right|=0+0+1 cdot(-1)^{3+1} cdot left| begin{array}{rrr}{8} & {-2} & {-12} \ {4} & {-2} & {-8} \ {4} & {2} & {0}end{array}right|+0$$
Полученный определитель третьего порядка также разложим по элементам строки и столбца, предварительно получив нули,
например, в первом столбце. Для этого от первой строки отнимаем две вторые строки, а от третьей — вторую:
$$left| begin{array}{rrr}{8} & {-2} & {-12} \ {4} & {-2} & {-8} \ {4} & {2} & {0}end{array}right|=left| begin{array}{rrr}{0} & {2} & {4} \ {4} & {-2} & {-8} \ {0} & {4} & {8}end{array}right|=4 cdot(-1)^{2+2} cdot left| begin{array}{ll}{2} & {4} \ {4} & {8}end{array}right|=$$
$$=4 cdot(2 cdot 8-4 cdot 4)=0$$
Ответ. $left| begin{array}{cccc}{9} & {8} & {7} & {6} \ {5} & {4} & {3} & {2} \ {1} & {0} & {1} & {2} \ {3} & {4} & {5} & {6}end{array}right|=0$
Замечание
Последний и предпоследний определители можно было бы и не вычислять,
а сразу сделать вывод о том, что они равны нулю, так как содержат пропорциональные строки.
Приведение определителя к треугольному виду
С помощью элементарных преобразований над строками или столбцами определитель приводится к треугольному виду и тогда его
значение, согласно свойствам определителя, равно произведению
элементов стоящих на главной диагонали.
Пример
Задание. Вычислить определитель
$Delta=left| begin{array}{rrrr}{-2} & {1} & {3} & {2} \ {3} & {0} & {-1} & {2} \ {-5} & {2} & {3} & {0} \ {4} & {-1} & {2} & {-3}end{array}right|$ приведением его к треугольному виду.
Решение. Сначала делаем нули в первом столбце под главной диагональю. Все преобразования
будет выполнять проще, если элемент $a_{11}$ будет
равен 1. Для этого мы поменяем местами первый и второй столбцы определителя, что, согласно свойствам определителя,
приведет к тому, что он сменит знак на противоположный:
$$Delta=left| begin{array}{rrrr}{-2} & {1} & {3} & {2} \ {3} & {0} & {-1} & {2} \ {-5} & {2} & {3} & {0} \ {4} & {-1} & {2} & {-3}end{array}right|=-left| begin{array}{rrrr}{1} & {-2} & {3} & {2} \ {0} & {3} & {-1} & {2} \ {2} & {-5} & {3} & {0} \ {-1} & {4} & {2} & {-3}end{array}right|$$
Далее получим нули в первом столбце, кроме элемента $a_{11}$ ,
для этого из третьей строки вычтем две первых, а к четвертой строке прибавим первую, будем иметь:
$$Delta=-left| begin{array}{rrrr}{1} & {-2} & {3} & {2} \ {0} & {3} & {-1} & {2} \ {0} & {-1} & {-3} & {-4} \ {0} & {2} & {5} & {-1}end{array}right|$$
Далее получаем нули во втором столбце на месте элементов, стоящих под главной диагональю. И снова, если
диагональный элемент будет равен $pm 1$ , то
вычисления будут более простыми. Для этого меняем местами вторую и третью строки (и при этом меняется на
противоположный знак определителя):
$$Delta=left| begin{array}{rrrr}{1} & {-2} & {3} & {2} \ {0} & {-1} & {-3} & {-4} \ {0} & {3} & {-1} & {2} \ {0} & {2} & {5} & {-1}end{array}right|$$
Далее делаем нули во втором столбце под главной диагональю, для этого поступаем следующим образом:
к третьей строке прибавляем три вторых, а к четвертой — две вторых строки, получаем:
$$Delta=left| begin{array}{rrrr}{1} & {-2} & {3} & {2} \ {0} & {-1} & {-3} & {-4} \ {0} & {0} & {-10} & {-10} \ {0} & {0} & {-1} & {-9}end{array}right|$$
Далее из третьей строки выносим (-10) за определитель и делаем нули в третьем столбце под
главной диагональю, а для этого к последней строке прибавляем третью:
$$Delta=-10 left| begin{array}{rrrr}{1} & {-2} & {3} & {2} \ {0} & {-1} & {-3} & {-4} \ {0} & {0} & {1} & {1} \ {0} & {0} & {-1} & {-9}end{array}right|=$$
$$=-10 cdot left| begin{array}{cccc}{1} & {-2} & {3} & {2} \ {0} & {-1} & {-3} & {-4} \ {0} & {0} & {1} & {1} \ {0} & {0} & {0} & {-8}end{array}right|=(-10) cdot 1 cdot(-1) cdot 1 cdot(-8)=-80$$
Ответ. $Delta=-80$
Теорема Лапласа
Теорема
Пусть $Delta$ — определитель
$n$-го порядка. Выберем в нем произвольные
$k$ строк (или столбцов), причем
$k leq n-1$ . Тогда сумма произведений всех
миноров
$k$-го порядка, которые содержатся в выбранных
$k$ строках (столбцах), на их
алгебраические дополнения равна определителю.
Пример
Задание. Используя теорему Лапласа, вычислить определитель
$left| begin{array}{rrrrr}{2} & {3} & {0} & {4} & {5} \ {0} & {1} & {0} & {-1} & {2} \ {3} & {2} & {1} & {0} & {1} \ {0} & {4} & {0} & {-5} & {0} \ {1} & {1} & {2} & {-2} & {1}end{array}right|$
Решение. Выберем в данном определителе пятого порядка две строки —
вторую и третью, тогда получаем (слагаемые, которые равны нулю, опускаем):
$$left| begin{array}{rrrrr}{2} & {3} & {0} & {4} & {5} \ {0} & {1} & {0} & {-1} & {2} \ {3} & {2} & {1} & {0} & {1} \ {0} & {4} & {0} & {-5} & {0} \ {1} & {1} & {2} & {-2} & {1}end{array}right|=left| begin{array}{cc}{1} & {-1} \ {4} & {-5}end{array}right| cdot(-1)^{2+4+2+4} cdot left| begin{array}{ccc}{2} & {0} & {5} \ {3} & {1} & {1} \ {1} & {2} & {1}end{array}right|+$$
$$+left| begin{array}{ll}{1} & {2} \ {4} & {0}end{array}right| cdot(-1)^{2+4+2+5} cdot left| begin{array}{rrr}{2} & {0} & {4} \ {3} & {1} & {0} \ {1} & {2} & {-2}end{array}right|+left| begin{array}{cc}{-1} & {2} \ {-5} & {0}end{array}right| cdot(-1)^{2+4+5} cdot left| begin{array}{ccc}{2} & {3} & {0} \ {3} & {2} & {1} \ {1} & {1} & {2}end{array}right|=$$
$$=-23+128+90=195$$
Ответ. $left| begin{array}{rrrrr}{2} & {3} & {0} & {4} & {5} \ {0} & {1} & {0} & {-1} & {2} \ {3} & {2} & {1} & {0} & {1} \ {0} & {4} & {0} & {-5} & {0} \ {1} & {1} & {2} & {-2} & {1}end{array}right|=195$
Читать дальше: обратная матрица.
Найти определитель (детерминант) матрицы онлайн
На данной странице калькулятор поможет найти определитель матрицы онлайн с подробным решением. При решении можно выбрать правило треугольника, правило Саррюса. Разложение определителя по строке или столбцу. Приведение определителя к треугольному виду. Для расчета задайте целые или десятичные числа.
Определитель матрицы
Размерность матрицы:
Павило: