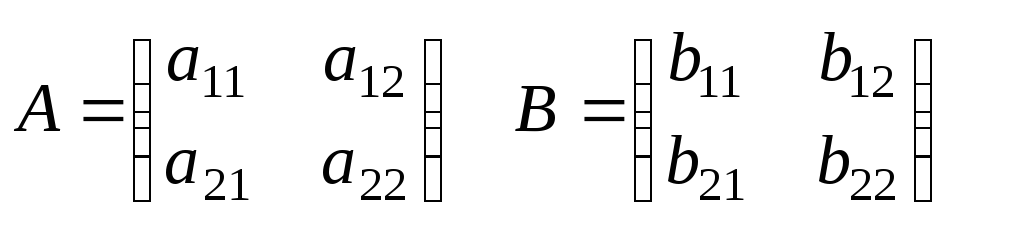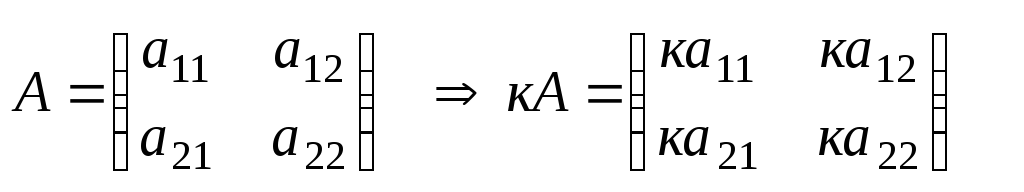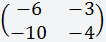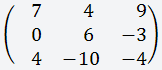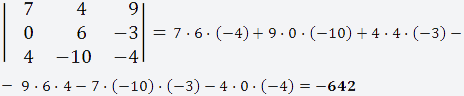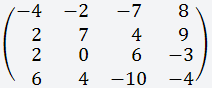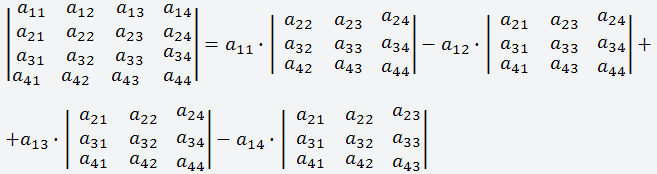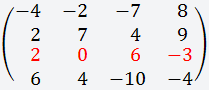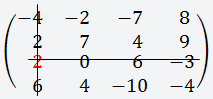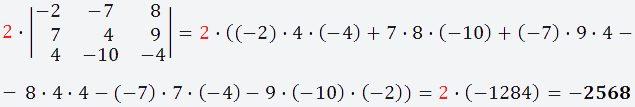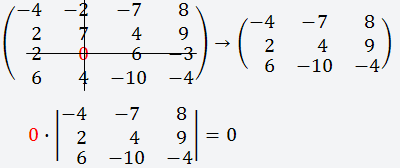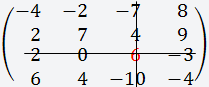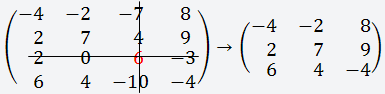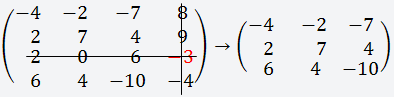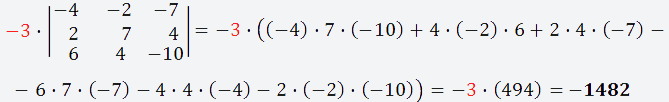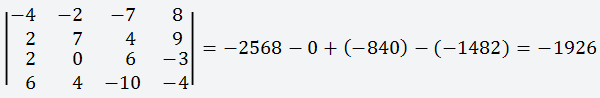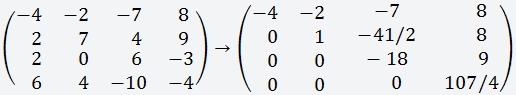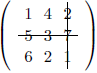Это многочлен от элементов квадратной матрицы (если матричные элементы являются числами, то матричный определитель также будет числом).
Есть много способов вычислить определитель квадратной матрицы. Наш онлайн-калькулятор рассчитывает определитель, используя метод Гаусса, или путем разложения определителя на элементы любой строки или столбца.
Онлайн-калькулятор
Чтобы вычислить определитель по методу Гаусса, начальная матрица приведена к верхней треугольной форме с помощью элементарных преобразований, а определитель исходной матрицы не изменяется и равен произведению элементов на главной диагонали верхняя треугольная матрица.
Чтобы вычислить определитель, развернув его на элементы строки или столбца, сначала выберите строку или столбец, по которым определитель будет разложен. Удобнее всего расположить определитель по строке (или столбцу) с максимальным количеством нулевых элементов. Если в исходной матрице нет таких строк (или столбцов), вы можете выбрать любую строку (или столбец).
Результирующее разложение представляет собой линейную комбинацию определителей, порядок которых на единицу меньше исходного. Каждый из этих определителей вычисляется снова путем расширения выбранной строки или столбца.
Таким образом, рассмотренный метод расчета определителя является рекурсивным процессом.
Разберем данный метод на конкретных примерах.
Пример 1
Дано:
A=(1514126715457)A= begin{pmatrix} 15 & 14 & 12 \ 6 & 7 & 1 \ 54 & 5 & 7 end{pmatrix}
Решение:
Делим 1 строку на 15, получаем:
(114150.86715457)begin{pmatrix} 1 & {14 over 15} & 0.8 \ 6 & 7 & 1 \ 54 & 5 & 7 end{pmatrix}
Делим 2 строку на 6, получаем:
(114150.8176165457)begin{pmatrix} 1 & {14 over 15} & 0.8 \ 1 & {7 over 6} & {1 over 6} \ 54 & 5 & 7 end{pmatrix}
Делим 3 строку на 54, получаем:
(114150.8176161554754)begin{pmatrix} 1 & {14 over 15} & 0.8 \ 1 & {7 over 6} & {1 over 6} \ 1 & {5 over 54} & {7 over 54} end{pmatrix}
Вычитаем 1-ю строку из последующих
(114150.80730−19300−227270−181270)begin{pmatrix} 1 & {14 over 15} & 0.8 \ 0 & {7 over 30} & -{19 over 30} \ 0 & -{227 over 270} & -{181 over 270} end{pmatrix}
Делим 2 строку на 7/30, получаем:
(114150.801−1970−227270−181270)begin{pmatrix} 1 & {14 over 15} & 0.8 \ 0 & 1 & -{19 over 7} \ 0 & -{227 over 270} & -{181 over 270} end{pmatrix}
Делим 3 строку на -227/270, получаем:
(114150.801−19701181227)begin{pmatrix} 1 & {14 over 15} & 0.8 \ 0 & 1 & -{19 over 7} \ 0 & 1 & {181 over 227} end{pmatrix}
Вычитаем 2-ю строку из последующих
(114150.801−1970055801589)begin{pmatrix} 1 & {14 over 15} & 0.8 \ 0 & 1 & -{19 over 7} \ 0 & 0 & {5580 over 1589} end{pmatrix}
Умножаем первые числа каждой строки (которые использовались при сокращении):
det=15⋅6⋅54⋅730⋅(−227270)⋅55801589=−3348det = 15 cdot 6 cdot 54 cdot {7 over 30} cdot left(-{227 over 270}right) cdot {5580 over 1589} = -3348
∣A∣=(1514126715457)=−3348|A| = begin{pmatrix} 15 & 14 & 12 \ 6 & 7 & 1 \ 54 & 5 & 7 end{pmatrix} = -3348
Ответ будет равен ∣A∣=−3348|A| = -3348
В следующем примере разберем случай дробных узлов матрицы, как более сложный вариант:
Пример 2
Дано:
A=(2718141512131425217)A= begin{pmatrix} {2 over 7} & {1 over 8} & {14 over 15} \ {1 over 2} & {1 over 3} & 1 \ {4 over 2} & {5 over 2} & {1 over 7} end{pmatrix}
Решение:
Делим 1 строку на 2/7, получаем:
(1716491512131425217)begin{pmatrix} 1 & {7 over 16} & {49 over 15} \ {1 over 2} & {1 over 3} & 1 \ {4 over 2} & {5 over 2} & {1 over 7} end{pmatrix}
Делим 2 строку на 1/2, получаем:
(171649151232425217)begin{pmatrix} 1 & {7 over 16} & {49 over 15} \ 1 & {2 over 3} & 2 \ {4 over 2} & {5 over 2} & {1 over 7} end{pmatrix}
Делим 3 строку на 4/2, получаем:
(171649151232154114)begin{pmatrix} 1 & {7 over 16} & {49 over 15} \ 1 & {2 over 3} & 2 \ 1 & {5 over 4} & {1 over 14} end{pmatrix}
Вычитаем 1-ю строку из последующих
(1716491501148−191501316−671210)begin{pmatrix} 1 & {7 over 16} & {49 over 15} \ 0 & {11 over 48} & -{19 over 15} \ 0 & {13 over 16} & -{671 over 210} end{pmatrix}
Делим 2 строку на 11/48, получаем:
(1716491501−3045501316−671210)begin{pmatrix} 1 & {7 over 16} & {49 over 15} \ 0 & 1 & -{304 over 55} \ 0 & {13 over 16} & -{671 over 210} end{pmatrix}
Делим 3 строку на 13/16, получаем:
(1716491501−3045501−53681365)begin{pmatrix} 1 & {7 over 16} & {49 over 15} \ 0 & 1 & -{304 over 55} \ 0 & 1 & -{5368 over 1365} end{pmatrix}
Вычитаем 2-ю строку из последующих
(1716491501−30455002394415015)begin{pmatrix} 1 & {7 over 16} & {49 over 15} \ 0 & 1 & -{304 over 55} \ 0 & 0 & {23944 over 15015} end{pmatrix}
Умножаем первые числа каждой строки (которые использовались при сокращении):
det=27⋅12⋅42⋅1148⋅1316⋅2394415015=299335280det = {2 over 7} cdot {1 over 2} cdot {4 over 2} cdot {11 over 48} cdot {13 over 16} cdot {23944 over 15015} = {2993 over 35280}
∣A∣=(2718141512131425217)=299335280|A| = begin{pmatrix} {2 over 7} & {1 over 8} & {14 over 15} \ {1 over 2} & {1 over 3} & 1 \ {4 over 2} & {5 over 2} & {1 over 7} end{pmatrix} = {2993 over 35280}
Ответ будет определен следующим образом: ∣A∣=299335280|A| = {2993 over 35280}
Не получается понять, как правильно вычислять с помощью матрицы? В таком случае, советуем вам заказать решение задачи по алгебре на Студворк!
Найти определитель матрицы методом Гаусса
Елена Борисовна Калюжная
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Определитель матрицы – это число, являющееся её параметром-характеристикой. Через определитель выполняются многие действия, связанные с матрицами, например, поиск неизвестных из систем уравнений и не только.
В этой статье рассказано про получение определителя методом Гаусса, также иногда такой способ называют понижением порядка определителя. Помимо приведённого здесь способа также детерминант можно сосчитать через миноры или используя правила Саррюса и треугольников.
Свойства определителя квадратной матрицы
- Определитель транспонированной матрицы $A^T$ равен определителю матрицы $A$:
$|A^T| = |A|$ - Определитель квадратной матрицы с нулевой строчкой или столбцом равен нулю.
- Перемещая какие-то строчки или столбцы матрицы на места друг друга, знак определителя изменится на противоположный.
- Наличие одинаковых строчек, или таких строчек, которые станут одинаковыми после вынесения коэффициента, делают её определитель нулевым.
- При умножении членов какой-то матричной строчки или столбца $A$ на некий коэффициент $k$, определитель новой полученной матрицы является определителем произведения $A$ и $k$.
- При сложении членов матрицы $A$, находящихся на одной строчке (или в одном столбце) с элементами другой её строчки или столбца, помноженными на некое число $k$, не равное нулю, определитель полученной матрицы будет иметь то же значение, что и определитель матрицы $A$.
- Определитель некой матрицы $A$ равен сумме произведений членов какой-либо строчки или столбца на её алгебраические дополнения.
Алгоритм для подсчёта детерминанта методом Гаусса
Чтобы найти определитель матрицы методом Гаусса, необходимо:
- Привести матрицу к верхнетреугольной или нижнетреугольной форме используя разрешённые над матрицей преобразования, называемые также элементарными.
- Сосчитать произведение всех членов матрицы, принадлежащих главной матричной диагонали полученной треугольной матрицы (эта диагональ проходит слева-направо сверху-вниз). При осуществлении подсчётов для вычисления определителя матрицы методом Гаусса нужно помнить, что при перестановке строчек или столбцов необходимо поменять знак детерминанта в конце решения на противоположный.
Замечание 1
Важно: не следует умножать или делить отдельные строчки матрицы на какие-либо числа во время процесса вычисления, так как это изменит итоговое значение. В случае же если всё же домножили строчку матрицы на какой-либо коэффициент, не забудьте вынести его обратное значение как множитель перед матрицей и домножить на это число итоговый ответ.
«Найти определитель матрицы методом Гаусса» 👇
Пример 1
Найти определитель матрицы методом Гаусса.
$A = left( begin{array}{ccc} 0 & 1 &2 \ 3 & 4 & 5 \ 1 & 1 & 3 \ end{array} right)$
Переставляем верхнюю и третью строчки и выносим знак минус после перестановки:
$A = — left( begin{array}{ccc} 1 & 1 & 3 \ 0 & 1 &2 \ 3 & 4 & 5 \ 0 & 1 &2 end{array} right)$
Затем умножаем первую строчку на $3$ и вычитаю из второй:
$A = — left( begin{array}{ccc} 1 & 1 & 3 \ 0& 1 & -4 \ 0 & 1 &2 \ end{array} right)$
Вычитаем из третьей строчки вторую:
$A = — left( begin{array}{ccc} 1 & 1 & 3 \ 0& 1 & -4 \ 0 & 0 &6 \ end{array} right)$
Полученная матрица является нижнетреугольной, следовательно, теперь можно сосчитать её детерминант:
$det(A) = — ( 1 cdot 1 cdot 6) = -6$
Пример 2
Примените метод Гаусса для вычисления определителя матрицы 4 порядка:
$A = left( begin{array}{cccc} 1 & 2 & 3 & 4 \ 2 & 0 & 2 & 3 \ 3 & 5 & 1 & 0 \ 4 & 1 & 0 & 0 \ end{array} right)$
Сделаем перестановку крайнего столбца с последним и третьего столбец со вторым. Это не изменит знак конечного значения определителя, так как смена позиций применяется дважды:
$A = left( begin{array}{cccc} 4 & 3 & 2 & 1 \ 3 & 2 & 0 & 2 \ 0 & 1 & 5 & 3 \ 0 & 0 & 1 & 4 \ end{array} right)$
Вычитаю из первой строчки вторую:
$A = left( begin{array}{cccc} 1 & 1 & 2 & -1 \ 3 & 2 & 0 & 2 \ 0 & 1 & 5 & 3 \ 0 & 0 & 1 & 4 \ end{array} right)$
Складываю умноженную на $3$ верхнюю строчку со второй:
$A = left( begin{array}{cccc} 1 & 1 & 2 & -1 \ 0 & -1 & -6 & 5 \ 0 & 1 & 5 & 3 \ 0 & 0 & 1 & 4 \ end{array} right)$
Прибавляю к предпоследней строке вторую:
$A = left( begin{array}{cccc} 1 & 1 & 2 & -1 \ 0 & -1 & -6 & 5 \ 0 & 0 & -1 & 8 \ 0 & 0 & 1 & 4 \ end{array} right)$
Прибавляю к нижней строчке предпоследнюю:
$A = left( begin{array}{cccc} 1 & 1 & 2 & -1 \ 0 & -1 & -6 & 5 \ 0 & 0 & -1 & 8 \ 0 & 0 & 0 & 12 \ end{array} right)$
Матрица стала треугольной, теперь найдём её детерминант:
$det(A) = 1 cdot (-1) cdot (-1) cdot 12 = 12$.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Дата последнего обновления статьи: 16.12.2022
Вычисление определителя методом Гаусса
Вычислим определитель методом Гаусса.
Суть метода состоит в следующем:
определитель приводится к треугольному
виду с помощью элементарных преобразований,
и тогда он равен произведению элементов,
стоящих на главной диагонали.
Идея метода состоит в следующем: пусть
дан определитель третьего порядка

элементдолжен быть равен
,
для этого первую строку разделим на.
Получим определитель вида

Обнулим элементы, стоящие в первом
столбце, кроме первого. Для этого из
второй строки вычтем первую, умноженную
на
,
далее из третьей строки вычтем первую,
умноженную на.
Получим определитель вида
Обозначим его элементы буквой с, тогда

Теперь надо обнулить элемент
.
Элементдолжен быть равен
,
для этого вторую строку разделим на.
Получим определитель вида
Далее из третьей строки вычтем вторую,
умноженную на
.
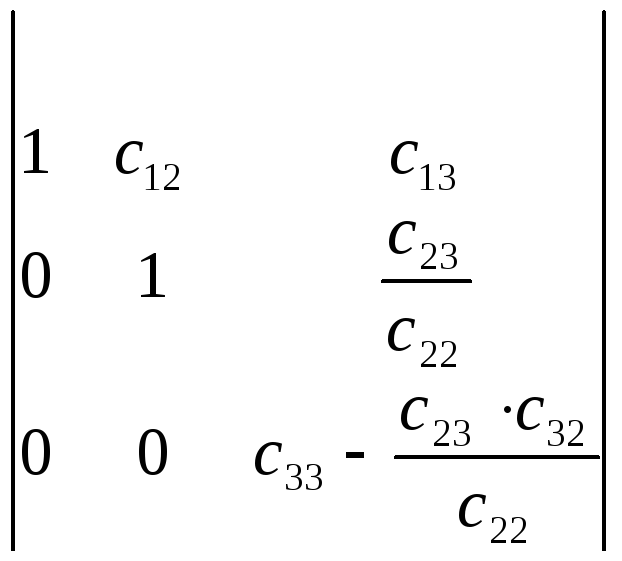
Обозначим его элементы буквой t,
тогда

Вот мы привели определитель к треугольному
виду, теперь он равен
.
Разберем теперь это на конкретном
примере.
Пример 4:Вычислить определитель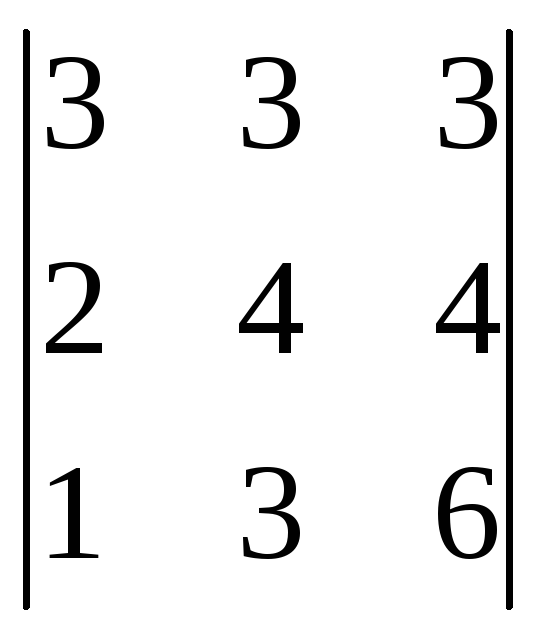
Решение: Поменяем местами первую и
третью строки (при замене двух столбцов
(строк) определитель меняет знак на
противоположный).
Получили
Из второй строки вычтем первую, умноженную
на 2, далее из третьей строки вычтем
первую, умноженную на 3. Получили
Далее из третьей строки вычтем вторую,
умноженную на 3.
Получили —
§2.Матрицы Виды матриц
Определение 7: Если в матрицеmстрок иnстолбцов, то она
называетсяразмерностьюmnи пишут
.
Определение 8: Если,
то матрица называется квадратной.
Определение 9:Матрица, состоящая
лишь из одной строки (столбца) называется
матрицей-строкой (столбцом).
Определение 10:Матрица, состоящая
из нулей, называется нулевой матрицей.
Определение 11:Диагональной матрицей
называется квадратная матрица, у которой
все элементы, не принадлежащие главной
диагонали равны нулю.
Определение 12:Единичной матрицей
называется диагональная матрица, у
которой все элементы, стоящие на главной
диагонали равны единице.
Определение 13:Треугольной называется
квадратная матрица, у которой элементы,
расположенные по одну сторону от главной
диагонали равны нулю.
Действиянад матрицами.
Определение 14: Две матрицы считаются
равными, если они имеют одинаковое число
строк и столбцов и равные соответствующие
элементы.
Пример 5:
Матрицы А и В равны, т.е.
Определение 15: Суммой (разностью)
матриц А и В называется такая матрица
С, у которой каждый элемент равен.
Пример 6: Найти матрицу,
если
Решение:
Cвойства сложения
А+В=В+А(переместительное)
20А+О=А, где О-нулевая матрица
30 А+(В+С)=(А+В)+С (дистрибутивное)
40А+(-А)=О, где – А противоположная
матрица
(т.е. элементы имеют противоположные
знаки)
Определение 16: Произведением матрицы
А на число
называется матрица, полученная из
данной умножением всех ее элементов на
число.
Пример 7:
Умножение матиц
Это действие распространяется на так
называемые согласованные матрицы.
Определение 17: Матрица А называется
согласованной с матрицей В, если число
столбцов у матрицы А равно числу строк
у матрицы В.
Пример 8: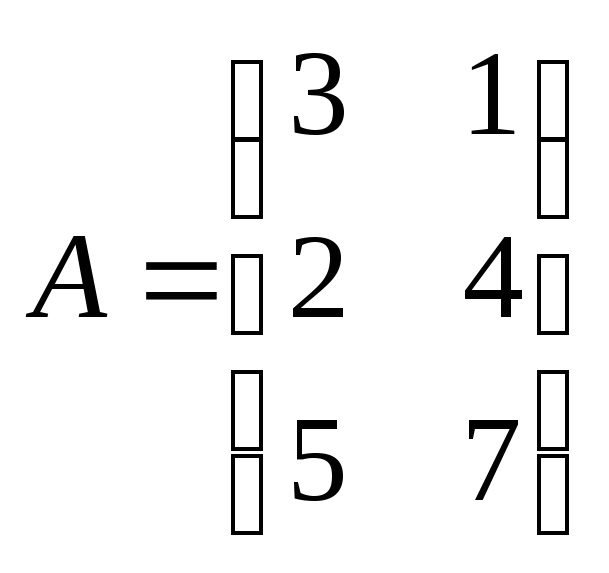
— согласованные

— несогласованные

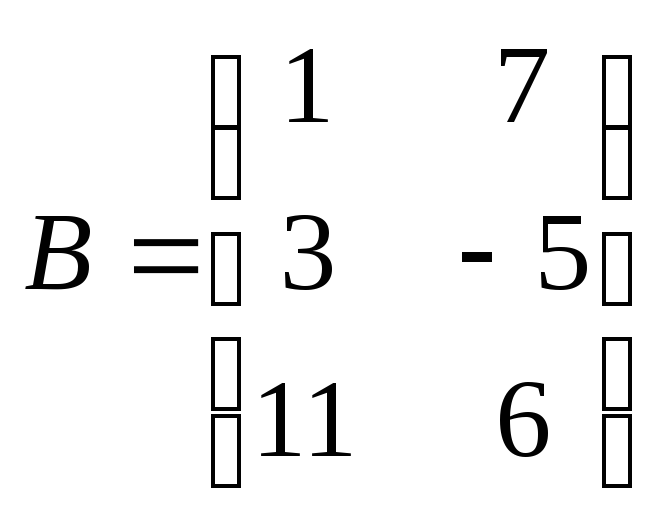
Определение 18: Произведением двух
матриц А и В называется такая матрица
С, каждый элемент которой равен сумме
произведений элементовiстроки матрицы А на соответствующие
элементыj-го столбца
матрицы В.
Если матрица А имеет размерность
,
а матрица В,
то.
Пример 9: Умножить матрицы
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание
- Предупреждение
- Примеры вычисления определителя матрицы
- Определение
- Обозначения
- Свойства определителя
- Минор матрицы
- Алгебраическое дополнение элемента матрицы
- Порядок определителя
- Вычисление определителя матрицы
- Вычисление определителя матрицы 2×2
- Вычисление определителя матрицы 3×3
- Вычисление определителя матрицы 4×4
Пример вычисления определителя (детерминанта) матрицы
Определитель матрицы — является многочленом от элементов квадратной матрицы (если элементы матрицы это числа, тогда определитель матрицы тоже будет числом).
Для нахождения определителя матрицы, исходная матрица должна быть квадратной.
Дана матрица размером 2х2;
Что бы вычислить определитель матрицы 2х2 нужно из произведения элементов главной диагонали, вычесть произведение элементов побочной диагонали;
Дана матрица размером 3х3;
Что бы вычислить определитель матрицы 3х3 нужно воспользоваться формулой;
Подставляем наши значения в формулу;
Дана матрица размером 4х4;
Есть два способа вычисления определителя матрицы:
По определению — через разложение по строке или столбцу;
По методу Гаусса — приведение матрицы к треугольному виду (этот способ лучше использовать для решения матриц, размером 4х4 и более).
Решим пример первым способом (по определению — через разложение по строке или столбцу)
Чтобы вычислить определитель матрицы, нужно воспользоваться следующей формулой, в ней рассмотрен пример разложения матрицы по первой строке;
Выбираем строку или столбец (любую), лучше всего выбирать строку или столбец, где больше нулей, для удобства вычисления; В данном случае мы выбираем третью строку, так как в ней присутствует ноль;
Берём первый элемент этой строки (2); Теперь вычёркиваем третью строку и первый столбец;
Получаем матрицу 3х3;
Согласно формуле, мы умножаем выбранный нами элемент на определитель получившейся матрицы;
Вычисление определителя матрицы 3х3, мы рассматривали в примере №2
Далее делаем всё тоже самое, что и в шаге два, только берём второй элемент данной строки (0) и вычёркиваем третью строку и второй столбец;
Так как этот элемент равен нулю, то ни чего не нужно считать и так всё ясно;
Теперь берём третий элемент строки (6) и вычёркиваем третью строку и третий столбец;
Получаем матрицу 3х3;
Вычисляем определитель этой матрицы и умножаем на выбранный нами элемент (6)
Берём четвёртый элемент строки (-3) и вычёркиваем третью строку и четвёртый столбец;
Получаем матрицу 3х3;
Вычисляем определитель этой матрицы и умножаем на выбранный нами элемент (-3)
Чтобы вычислить определитель исходной матрицы, нужно сложить полученные результаты;
Опишем решение примера вторым способом (по методу Гаусса — приведение матрицы к треугольному виду)
Суть способа заключается в том, чтобы перед вычислением определителя, привести матрицу к треугольному виду. Если в ходе приведения матрицы к треугольному виду вы умножаете (делите) строку на число, то на это же число нужно будет умножить (разделить) полученный в конце определитель;
Пример приведения матрицы к треугольному виду мы уже рассматривали здесь
Итак, мы привили матрицу к треугольному виду;
Теперь чтобы вычислить определитель приведённой матрицы, нужно перемножить все элементы, стоящие на главной диагонали;
Данный онлайн калькулятор вычисляет определитель матрицы. Дается подробное решение. Для вычисления определителя матрицы выбирайте порядок (размер) квадратной матрицы. Введите данные в ячейки. Выберите метод решения и нажмите на кнопку «Вычислить». Теоретическую часть смотрите на странице определитель матрицы.
Предупреждение
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Примеры вычисления определителя матрицы
Пример 1. Найти определитель матрицы

Для вычисления определителя матрицы, приведем матрицу к верхнему треугольному виду.
Выбираем самый большой по модулю ведущий элемент столбца 1. Для этого меняем местами строки 1 и 2. При этом меняется знак определителя на «−»:

Исключим элементы 1-го столбца матрицы ниже главной диагонали. Для этого сложим строки 2,3 со строкой 1, умноженной на -1/78,-2/78 соответственно:
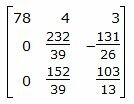
Исключим элементы 2-го столбца матрицы ниже главной диагонали. Для этого сложим строку 3 со строкой 2, умноженной на -5928/9048:

Мы привели матрицу к верхнему треугольному виду. Определитель матрицы равен произведению всех элементов главной диагонали (учитывая знак определителя):

Пример 2. Найти определитель матрицы A, разложением определителя по первой строке:

Для вычисления определителя матрицы методом разложения по первой строке, вычисляем произведение каждого элемента первой строки на соответствующее алгебраическое дополнение и суммируем полученные результаты:
Определение
Определитель (детерминант) квадратной матрицы A — это число, обладающее определенными свойствами, которое может быть получено из элементов матрицы рядом методов.
Обозначения
Пусть $ A = egin 1 & 4 & 2 5 & 3 & 7 6 & 2 & 1 end$
$det(A) = left|A
ight| = egin 1 & 4 & 2 5 & 3 & 7 6 & 2 & 1 end$
Свойства определителя
- Если матрица имеет строку или столбец, все элементы которого равны нулю, то ее определитель равен 0.
Пример 12
$egin 1 & 4 & 2 0 & 0 & 0 3 & 9 & 5 end= 0$ или $egin 1 & 4 & 0 4 & 2 & 0 3 & 9 & 0 end=0$
Если в матрице есть две одинаковых строки или два одинаковых столбца, то ее определитель равен 0.
Пример 13
$egin 1 & 4 & 2 1 & 4 & 2 3 & 9 & 5 end= 0$ или $egin 1 & 4 & 1 4 & 2 & 4 3 & 9 & 3 end=0$
Если в матрице есть две пропорциональных строки или два пропорциональных столбца, то ее определитель равен 0.
Пример 14
$egin 1 & 4 & 2 2 & 8 & 4 3 & 9 & 5 end= 0$ (две первые строки пропорциональны)
или
$egin 8 & 4 & 7 4 & 2 & 3 18 & 9 & 8 end=0$ (два первых столбца пропорциональны)
Если некоторая строка (столбец) является суммой или разностью других строк (столбцов), то определитель равен 0.
Пример 15
$egin 1 & 4 & 2 7 & 2 & 3 8 & 6 & 5 end= 0$ $R_ <1>+R_ <2>=R_<3>$ или
$ egin 9 & 12 & 3 1 & 8 & 7 5 & 7 & 2 end=0$ $C_<1>+C_<3>=C_<2>$
При вычислении определителя можно выносить общие множители целых строк или столбцов.
Пример 17
$egin 1 & 5 3 & 8 end$ $xlongequal<1>+R_<2>> egin 4 & 13 3 & 8 end$
Пример 18
$egin 1 & 5 3 & 8 end$ $xlongequal<1>+C_<2>> egin 6 & 5 11 & 8 end$
При вычислении определителя можно прибавлять или отнимать строки и столбцы, умноженные на произвольный коэффициент .
Пример 20
$egin 1 & 5 3 & 8 end$ $xlongequal<5C_<1>-C_<2>> egin 0 & 5 7 & 8 end$
Минор матрицы
Определитель матрицы, полученной вычеркиванием некоторых строк и столбцов матрицы, называется минором этой матрицы.
Пример 21
$A=egin 1 & 4 & 2 5 & 3 & 7 6 & 2 & 1 end$
Один из миноров матрицы A есть $egin 1 & 2 5 & 3 end$ (он получается вычеркиванием строки 3 и столбца 3 из матрицы A)
Другим минором является $egin 1 & 2 6 & 1 end$ (получается вычеркиванием строки 2 и столбца 2 из матрицы A)
Пример 22
$B=egin 2 & 5 & 1 & 3 4 & 1 & 7 & 9 6 & 8 & 3 & 2 7 & 8 & 1 & 4 end $
Один из миноров матрицы B есть $ egin 1 & 7 & 9 8 & 3 & 2 8 & 1 & 4 end$ (получается вычеркиванием строки 1 и столбца 1 из матрицы B)
Другим минором является $egin 1 & 7 8 & 3 end$ (получается вычеркиванием строк 1 и 4 и столбцов 1 и 4 из матрицы B)
Пусть $A= egin a_ <1,1>& a_ <1,2>& a_ <1,3>& . & . & a_<1,n> a_ <2,1>& a_ <2,2>& a_ <2,3>& . & . & a_<2,n> a_ <3,1>& a_ <3,2>& a_ <3,3>& . & . & a_<3,n> . & . & . & . & .& . a_ & a_ & a_ & . & . & a_ end$
Можно определить минор $Delta_$, полученный вычеркиванием строки i и столбца j, для любого элемента $a_$ квадратной матрицы A. Такой минор называется дополнительным.
Определить дополнительный минор элемента 2. Так как данный элемент находится в строке 2, столбце 1, видно, что это $a_<2,1>$.
Нужно вычеркнуть строку 2 и столбец 1 из матрицы A, после чего получаем
Минор, дополнительный к элементу 2, есть $Delta_ <2,1>= 7$.
Пример 24
$B=egin 1 & 4 & 2 5 & 3 & 7 6 & 2 & 1 end$
Нужно найти минор, дополнительный к элементу 7. Так как данный элемент находится в строке 2, столбце 3, видно, что это $a_<2,3>$.
Мы должны вычеркнуть строку 2 и столбец 3 из матрицы B, после чего мы получаем
Минор, дополнительный к элементу 7, — это $Delta_<2,3>= egin 1 & 4 6 & 2 end$
Пример 25
$C=egin 2 & 5 & 1 & 3 4 & 1 & 7 & 9 6 & 8 & 3 & 2 7 & 8 & 1 & 4 end$
Нужно найти минор, дополнительный к элементу 5. Так как данный элемент находится в строке 1, столбце 2, видно, что это $a_<1,2>$.
Мы должны вычеркнуть строку 1 и столбец 2 из матрицы C, после чего мы получаем
Минор, дополнительный к элементу 5, — это $Delta_<1,2>= egin 4 & 7 & 9 6 & 3 & 2 7 & 1 & 4 end$
Алгебраическое дополнение элемента матрицы
Каждому элементу $a_$ матрицы A соответствует алгебраическое дополнение $(-1)^cdotDelta_$. Например, алгебраическое дополнение $(-1)^<2+5>cdotDelta_<2,5>=(-1)^<7>cdotDelta_<2,5>= -Delta_ <2,5>$ соответствует элементу $a_<2,5>$.
Порядок определителя
Порядок определителя матрицы равен числу ее строк и столбцов.
Пример 26
$egin 1 & 4 6 & 2 end$ (матрица имеет 2 строки и 2 столбца, так что порядок определителя равен 2)
Пример 27
$egin 4 & 7 & 9 6 & 3 & 2 7 & 1 & 4 end$ (матрица имеет 3 строки и 3 столбца, так что порядок определителя равен 3)
Вычисление определителя матрицы
Определитель матрицы равен сумме произведений элементов любой строки или любого столбца и их алгебраических дополнений.
$left| A
ight| = egin a_ <1,1>& a_ <1,2>& a_ <1,3>& . & . & a_<1,n> a_ <2,1>& a_ <2,2>& a_ <2,3>& . & . & a_<2,n> a_ <3,1>& a_ <3,2>& a_ <3,3>& . & . & a_<3,n> . & . & . & . & .& . a_ & a_ & a_ & . & . & a_ end$
Можно посчитать определитель, например, используя строку i:
Либо же можно посчитать определитель, используя столбец j:
Вычисление определителя матрицы 2×2
Используем строку 1, чтобы вычислить определитель.
Заметим, что $ Delta_<1,1>= a_ <2,2>$ и $ Delta_<1,2>=a_<2,1>$
$ left| A
ight| =a_ <1.1>cdot a_<2,2>- a_ <1.2>cdot a_<2,1>$
$color < egina & b c & d end =a cdot d — b cdot c>$
Пример 28
$egin 2 & 5 3 & 8 end =2 cdot 8 — 3 cdot 5 = 16 -15 =1$
Пример 29
$egin -4 & 7 -2 & 9 end =-4 cdot 9 — 7 cdot (-2) = -36 -(-14) =-36 + 14 = — 22$
Вычисление определителя матрицы 3×3
Используем строку 1, чтобы вычислить определитель.
Упростить получение последней формулы можно следующим образом.
Начнем с того, что перепишем первые две строки под определителем как показано ниже.
Умножаем элементы на каждой из трех красных диагоналей (на главной диагонали и на диагоналях под ней) и складываем результаты:
$colorcdot a_<2,2>cdot a_<3,3>+ a_<2,1>cdot a_<3,2>cdot a_<1,3>+a_<3,1>cdot a_<1,2>cdot a_<2,3>>$
Умножаем элементы на каждой из трех синих диагоналей (на побочной диагонали и на диагоналях под ней) и складываем результаты:
Вычитая вторую сумму из первой, получаем формулу определителя:
Пример 30
$A=egin 1 & 4 & 3 2 & 1 & 5 3 & 2 & 1 end$
Пример 31
$A=egin 3 & 5 & 1 1 & 4 & 2 7 & 1 & 9 end$
$= 3cdot4cdot9 + 1cdot1cdot1 + 7cdot5cdot2 -(1cdot4cdot7 + 2cdot1cdot3 + 9cdot5cdot1) =$ $ 108 + 1 + 70 -(28 + 6 + 45)=79-79=100$
Элементы матрицы могут быть обозначены буквами. Вычисление их определителей можно упростить, используя свойства определителей. Например, можно вычислить определитель матрицы, в которой к какой-либо строке (или столбцу) прибавлена линейные комбинация других строк (столбцов).
$egin a & b & c c & a & b b & c & a end$ $ xlongequal<1>+C_<2>+C_<3>> egin a + b + c & b & c c + a + b & a & b b + c + a & c & a end = (a + b + c) cdot egin 1 & b & c 1 & a & b 1 & c & a end$
Вычисляем последней определитель:
$ = a^ <2>+ b^ <2>+ c^ <2>-acdot c — bcdot c — acdot b =$ $frac<1><2>cdot(2a^ <2>+2b^<2>+2c^ <2>-2acdot b -2acdot c-2bcdot c) =$ $frac<1><2>cdot(a^<2>-2acdot b + b^<2>+ a^<2>-2acdot c +c^<2>+b^<2>-2bcdot c + c^<2>)=$ $frac<1><2>cdot[(a-b)^<2>+(a-c)^<2>+(b-c)^<2>]$
В итоге получаем:
Пример 32
Вычислим определитель матрицы Вандермонде.
$egin 1 & 1 & 1 a & b & c a^ <2>& b^ <2>& c^ <2>end$
Используя свойства определителей, модифицируем строку 1 так, чтобы два элемента обратились в 0. В этом случае, когда мы используем полученную выше формулу для определителя матрицы 3×3, нет необходимости вычислять алгебраические дополнения этих элементов, поскольку их произведение будет равно 0.
Вычисление определителя матрицы 4×4
Вычислить определитель матрицы 4×4 можно с использованием общей формулы для определителя матрицы 3×3.
Но сначала надо использовать свойства определителей:
- Проверим, не выполняется ли одно из условий того, что определитель равен 0.
- Проверим, нельзя ли вынести общий множитель из одной или нескольких строк или столбцов.
- Проверим, не является ли данная матрица матрицей Вандермонде, возможно, такой, в которой некоторые строки или столбцы переставлены.
В любом из этих случаев нам пригодятся соответствующие методы вычисления определителей матриц 3×3. Модифицируем строку или столбец так, чтобы все его элементы, кроме одного, обратились в 0. Определитель будет равен произведению этого ненулевого элемента на его алгебраическое дополнение. В этом случае, алгебраическое дополнение — это определитель матрицы 3×3, который считается по уже известной формуле.
Пример 33
$egin 1 & 3 & 9 & 2 5 & 8 & 4 & 3 0 & 0 & 0 & 0 2 & 3 & 1 & 8 end$
Замечаем, что все элементы в строке 3 равны нулю, а значит, определитель равен 0.
Пример 34
$egin 1 & 3 & 1 & 2 5 & 8 & 5 & 3 0 & 4 & 0 & 0 2 & 3 & 2 & 8 end$
Замечаем, что $C_<1>$ равно $C_<3>$, следовательно, определитель равен 0.
Пример 35
$egin 1 & 3 & 9 & 2 5 & 8 & 4 & 3 10 & 16 & 18 & 4 2 & 3 & 1 & 8 end$
Замечаем, что строки 2 и 3 пропорциональны друг другу, следовательно, определитель равен 0.
Пример 36
$egin color <4>& 3 & 2 & 2 0 & 1 & -3 & 3 0 & -1 & 3 & 3 0 & 3 & 1 & 1 end$
Поскольку в столбце 1 только один элемент отличен от нуля, применяем общую формулу, используя этот столбец. Алгебраические дополнения нулевых элементов считать не надо, так как их произведения на эти элементы все равно будут равны нулю.

$=4(1cdot3cdot1 +(-1)cdot1cdot3+3cdot(-3)cdot3$ $-(3cdot3cdot3+3cdot1cdot1 +1cdot(-3)cdot(-1)))$ $=4(3-3-27-(27+3+3))=4cdot(-60)=-240$
Пример 37
$egin 4 & 3 & 2 & 2 0 & 1 & 0 & -2 1 & -1 & 3 & 3 2 & 3 & 1 & 1 end$
Чтобы изменить строку так, чтобы в ней стало больше нулей, нужно совершать операции со столбцами, и наоборот. Выбираем строку или столбец, содержащий элемент 1, поскольку из него можно получить любое число простым умножением.
Заметим, что в строке 2 уже есть два нулевых элемента. Достаточно обратить лишь еще один элемент в 0, чтобы осталось посчитать только одно алгебраическое дополнение единичного элемента.
$egin 4 & 3 & 2 & 2 0 & 1 & 0 & -2 1 & -1 & 3 & 3 2 & 3 & 1 & 1 end xlongequal<4>+2C_<2>>$ $egin 4 & 3 & 2 & 8 0 & color <1>& 0 & 0 1 & -1 & 3 & 1 2 & 3 & 1 & 7 end=$ 
$= 1cdot(-1)^<2+2>cdot egin 4 & 2 & 8 1 & 3 & 1 2 & 1 & 7 end=$
$=4cdot3cdot7 + 1cdot1cdot8 + 2cdot2cdot1$ $-(8cdot3cdot2 + 1cdot1cdot4 + 7cdot2cdot1) =$ $ 84 + 8 + 4- 48-4-14=30$
Пример 38
$egin 1 & -2 & 3 & 2 2 & 3 & 1 & -1 3 & 3 & 3 & 3 -1 & 4 & 2 & 1 end$
Можно вынести множитель 3 из строки 3:
$3cdot egin 1 & -2 & 3 & 2 2 & 3 & 1 & -1 1 & 1 & 1 & 1 -1 & 4 & 2 & 1 end$
Поскольку в строке 3 все элементы равны 1, легко обратить получить нули.
$egin 1 & -2 & 3 & 2 2 & 3 & 1 & -1 1 & 1 & 1 & 1 -1 & 4 & 2 & 1 end$ $ xlongequal <1>— C_<4>,C_<2>-C_<4>,C_<3>-C_<4>> egin -1 & -4 & 1 & 2 3 & 4 & 2 & -1 0 & 0 & 0 & color<1> -2 & 3 & 1 & 1 end$ $=1cdot(-1)^<3+4>cdot$ 
$=-((-1)cdot 4cdot 1 +3 cdot 3cdot1 + (-2)cdot (-4)cdot 2$ $- (1cdot 4cdot (-2) + 2cdot 3cdot (-1) + 1cdot (-4)cdot3))$ $=-(-4 + 9 + 16 + 8 + 6 + 12) =-47$
Пример 39
$egin 2 & 5 & 1 & 4 4 & 1 & 6 & 3 5 & 3 & 7 & 2 1 & 0 & 2 & 4 end$
Здесь мы можем использовать единицу из последней строки и обратить остальные элементы первого столбца в нули.
$egin 2 & 5 & 1 & 4 4 & 1 & 6 & 3 5 & 3 & 7 & 2 1 & 0 & 2 & 4 end$ $xlongequal<1>-2R_<4>,R_<2>-4R_<4>, R_<3>-5R_<4>> egin 0 & 5 & -3 & -4 0 & 1 & -2 & -13 0 & 3 & -3 & -18 color <1>& 0 & 2 & 4 end=$ 
Выносим общий множитель -1 из столбца 2 и еще раз -1 из столбца 3.
$ (-1)cdot(-1)cdot(-1)cdot egin 5 & 3 & 4 1 & 2 & 13 3 & 3 & 18 end=$ $(-1)cdot egin 5 & 3 & 4 1 & 2 & 13 3 & 3 & 18 end=$ $-[5cdot 2cdot 18 + 1cdot 3cdot 4+ 3cdot 3cdot 13 — (4cdot 2cdot 3cdot + 13cdot 3cdot 5 + 18cdot 3cdot 1)]=$ $-(180+12+117-24-195-54)=36$
Пример 40
$egin 4 & 7 & 2 & 3 1 & 3 & 1 & 2 2 & 5 & 3 & 4 1 & 4 & 2 & 3 end$
Мы видим элемент 1 в столбце 3, так что мы можем обратить остальные элементы строки 2 в нули.
$egin 4 & 7 & 2 & 3 1 & 3 & 1 & 2 2 & 5 & 3 & 4 1 & 4 & 2 & 3 end$ $xlongequal<1>-C_<3>, C_<2>-3C_<3>,C_<4>-2C_<3>> egin 2 & 1 & 2 & -1 0 & 0 & color <1>& 0 -1 & -4 & 3 & -2 -1 & -2 & 2 & -1 end=$ 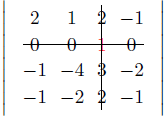
Выносим общий множитель -1 из строки 2 и еще раз -1 из строки 3.
$ (-1)cdot(-1)cdot(-1)cdot egin 2 & 1 & -1 1 & 4 & 2 1 & 2 & 1 end=$ $(-1)cdot egin 2 & 1 & -1 1 & 4 & 2 1 & 2 & 1 end=$ $-[2cdot 4cdot 1 + 1cdot 2cdot (-1)+ 1cdot 1cdot 2 — ((-1)cdot 4cdot 1 + 2cdot 2cdot 2 + 1cdot 1cdot 1)]=$ $-(8-2+2+4-8-1)=-3$
Пример 41
$egin 2 & 1 & 3 & 4 1 & 3 & 4 & 2 3 & 4 & 2 & 1 4 & 2 & 1 & 3 end$
Заметим, что все строки и все столбцы состоят из одних и тех же элементов, но в разном порядке. В таком случае мы можем сложить все строки или все столбцы.
$egin 2 & 1 & 3 & 4 1 & 3 & 4 & 2 3 & 4 & 2 & 1 4 & 2 & 1 & 3 end$ $xlongequal<1>+L_<2>+L_<3>+L_<4>> egin 10 & 10 & 10 & 10 1 & 3 & 4 & 2 3 & 4 & 2 & 1 4 & 2 & 1 & 3 end =$ $10cdot egin 1 & 1 & 1 & 1 1 & 3 & 4 & 2 3 & 4 & 2 & 1 4 & 2 & 1 & 3 end$ $xlongequal <1>— C_<4>,C_<2>-C_<4>,C_<3>-C_<4>>10cdot egin 0 & 0 & 0 & color<1> -1 & 1 & 2 & 2 2 & 3 & 1 & 1 1 & -1 & -2 & 3 end=$
$=10cdot1cdot(-1)^<1+4>$
$ = (-10)cdot egin -1 & 1 & 2 2 & 3 & 1 1 & -1 & -2 end=$ $(-10)cdot((-1)cdot 3cdot (-2) +2 cdot (-1)cdot2 + 1cdot 1cdot 1$ $-(2cdot 3cdot 1 + 1cdot (-1)cdot (-1) + (-2)cdot1cdot2))$ $= -10cdot(6 -4 +1 -6 — 1 + 4) =0$
Определителем
называется число, которое по определённому правилу можно поставить в соответствие любой квадратной матрице.
Наш онлайн калькулятор вычисляет определитель с использованием метода Гаусса или путем разложения определителя по элементам любой строки или столбца.
Для
вычисления определителя
методом Гаусса исходную матрицу путем элементарных преобразований приводят к
верхнетреугольному виду, при этом определитель исходной матрицы не меняется и равен произведению элементов на главной диагонали верхнетреугольной матрицы.
Определитель матрицы
вычисляется по формуле:
Для вычисления определителя путем его разложения по элементам строки или столбца, сначала выбирают строку или столбец по которой будут осуществлять разложение определителя. Наиболее удобно, раскладывать определитель по строке (или столбцу) с максимальным количеством нулевых элементов. Если таких строк (или столбцов) в исходной матрице нет, тогда можно выбрать любую строку (или столбец).
Ниже представлено вычисление определителя матрицы
,
при помощи его разложения по элементам первой строки:
Полученное разложение представляет собой линейную комбинацию определителей, порядок которых на единицу меньше исходного. Каждый из таких определителей вычисляется снова, путем разложения по выбранной строке или столбцу. Таким образом, рассматриваемый метод вычисления определителя представляет собой рекурсивный процесс.