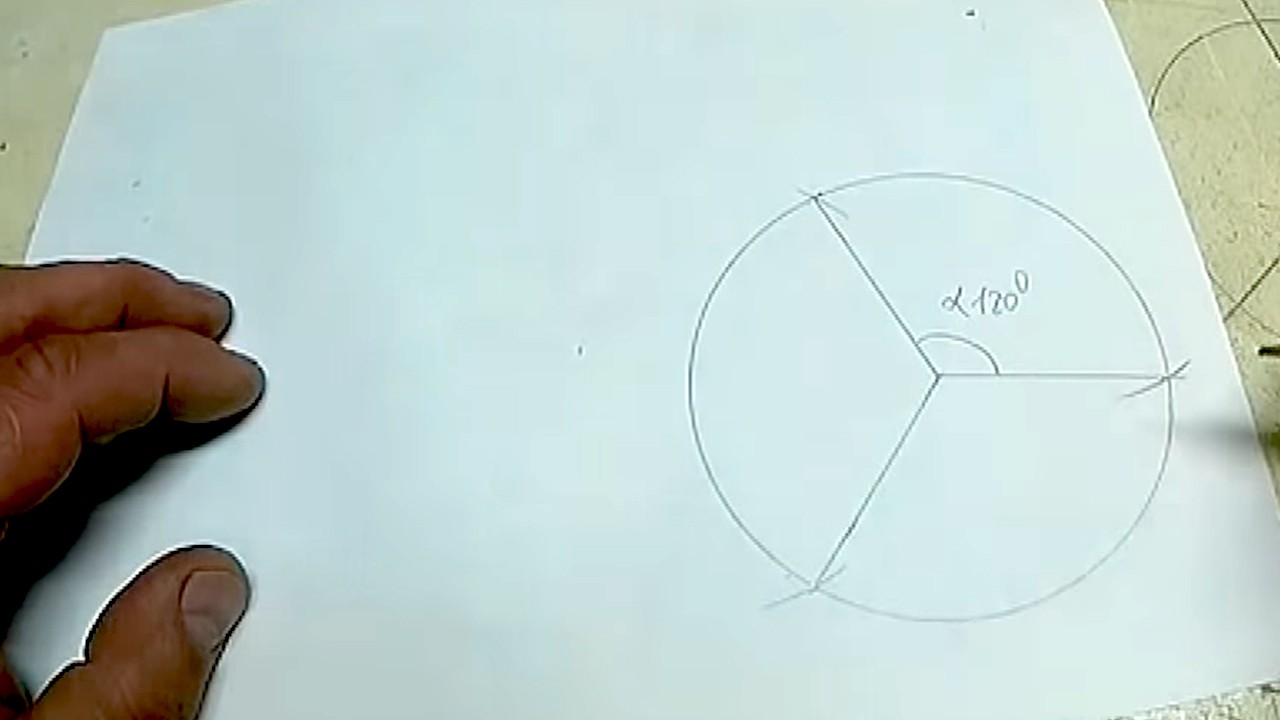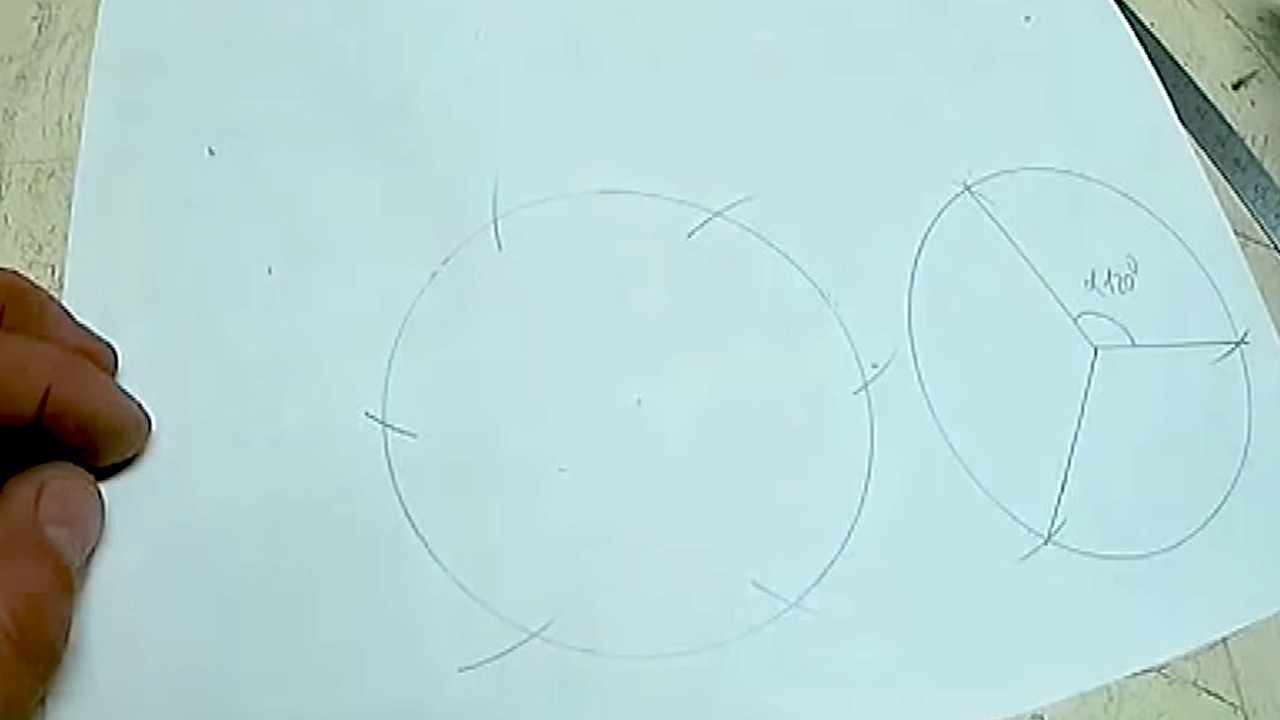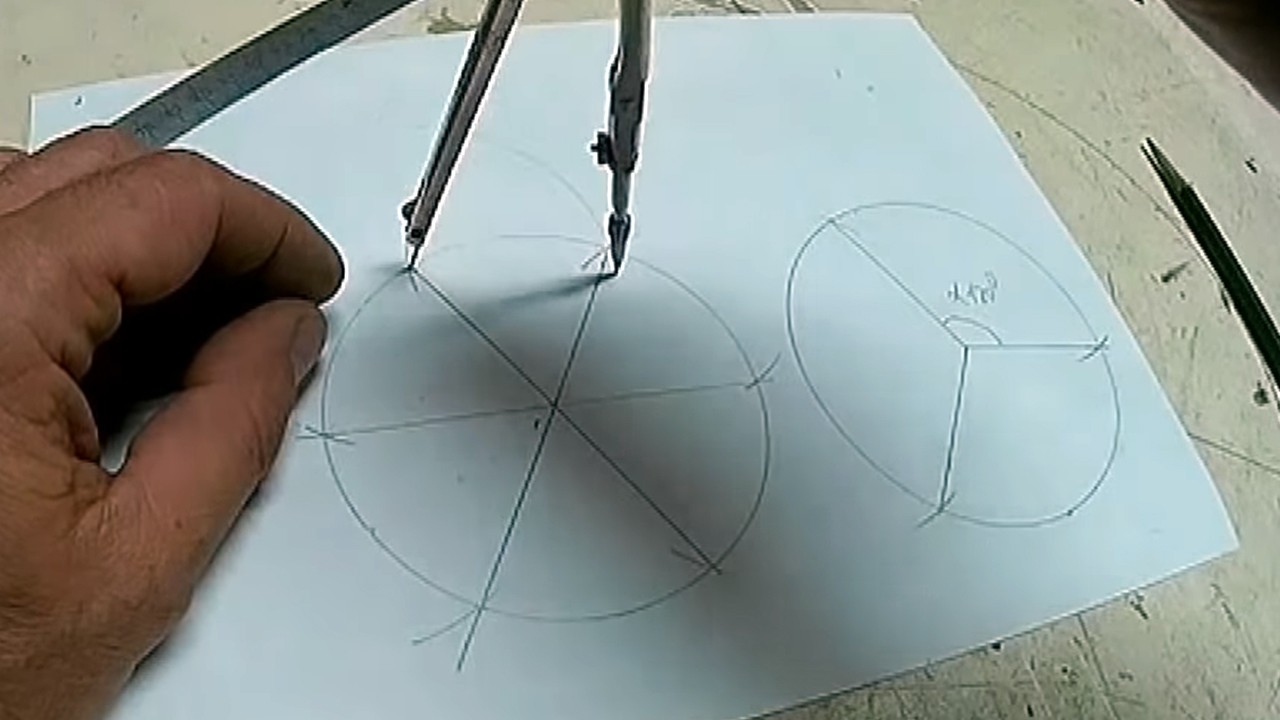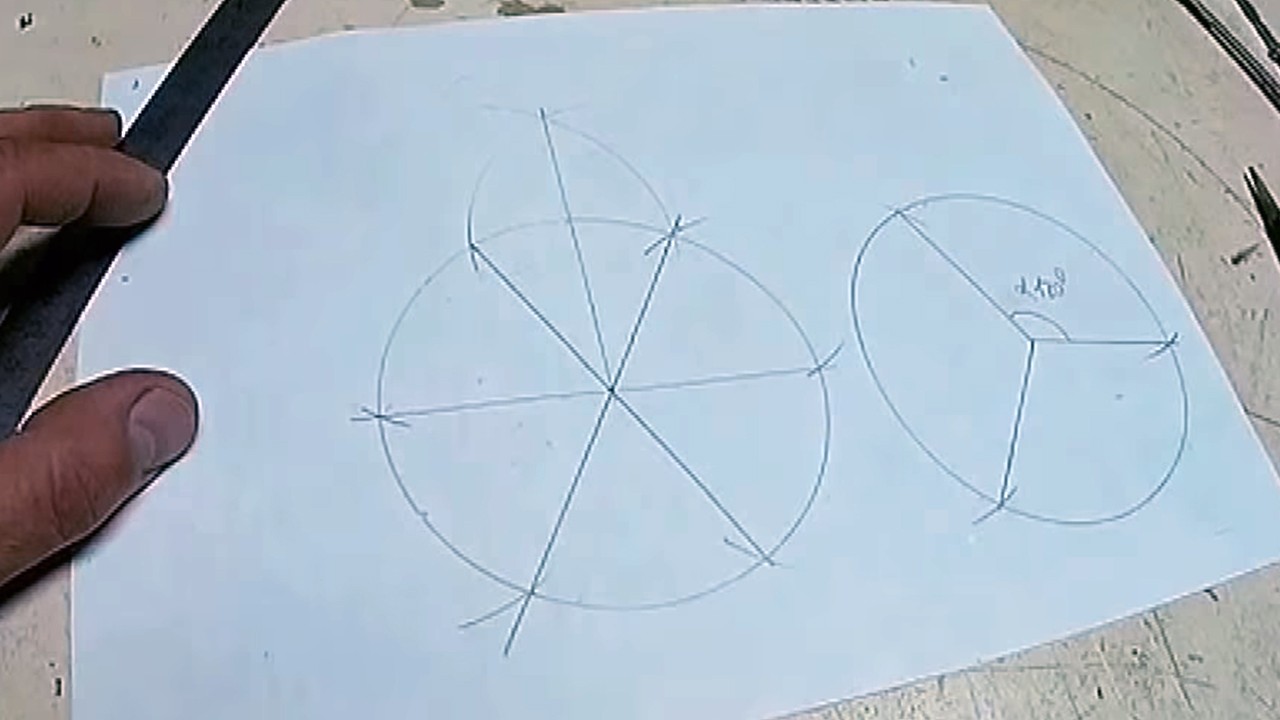Деление окружности на любое число равных частей
Как разделить окружность на заданное количество одинаковых частей, терминология при построении окружности, деление окружности на 3, 4, 5, 6, 8, 10 частей.
Термины при построениях окружности
Окружностью называется замкнутая кривая линия, каждая точка которой расположена на одинаковом расстоянии от одной точки О, называемой центром.
Прямые линии, соединяющие любую точку окружности с её центром, называют радиусами R.
Прямая АВ, соединяющая две точки окружности и проходящая через её центр О, называется диаметром D.
Части окружностей называются дугами.
Прямая СD, соединяющая две точки на окружности, называется хордой.
Прямая МN,которая имеет только одну общую точку с окружностью называется касательной.
Часть круга, ограниченная хордой СD и дугой, называется сигментом.
Часть круга, ограниченная двумя радиусами и дугой, называется сектором.
Две взаимно перпендикулярные горизонтальная и вертикальная линии, пересекающиеся в центре окружности, называются осями окружности.
Угол, образованный двумя радиусами КОА, называется центральным углом.
Два взаимно перпендикулярных радиуса составляют угол в 90 0 и ограничивают 1/4 окружности.
Деление окружности на 4 и 8 одинаковых частей
Проводим окружность с горизонтальной и вертикальной осями, которые делят её на 4-ре равные части. Проведённые с помощью циркуля или угольника под 45 0 , две взаимно перпендикулярные линии делят окружность на 8-мь равных частей.
Деление окружности на 3 и 6 равных частей (кратные 3 трём)
Для деления окружности на 3, 6 и кратное им количество частей, проводим окружность заданного радиуса и соответствующие оси. Деление можно начинать от точки пересечения горизонтальной или вертикальной оси с окружностью. Заданный радиус окружности последовательно откладывается 6-ть раз. Затем полученные точки на окружности последовательно соединяются прямыми линиями и образуют правильный вписанный шести-угольник. Соединение точек через одну даёт равносторонний треугольник, и деление окружности на три равные части.
Деление окружности на 5 и 10 равных частей
Построение правильного пятиугольника выполняется следующим образом. Проводим две взаимно перпендикулярные оси окружности равные диаметру окружности. Делим правую половину горизонтального диаметра пополам с помощью дуги R1. Из полученной точки «а» в середине этого отрезка радиусом R2 проводим дугу окружности до пересечения с горизонтальным диаметром в точке «b». Радиусом R3 из точки «1» проводят дугу окружности до пересечения с заданной окружностью (т.5) и получают сторону правильного пятиугольника. Расстояние «b-О» даёт сторону правильного десятиугольника.
Деление окружности на N-ное количество одинаковых частей (построение правильного многоугольника с N сторон)
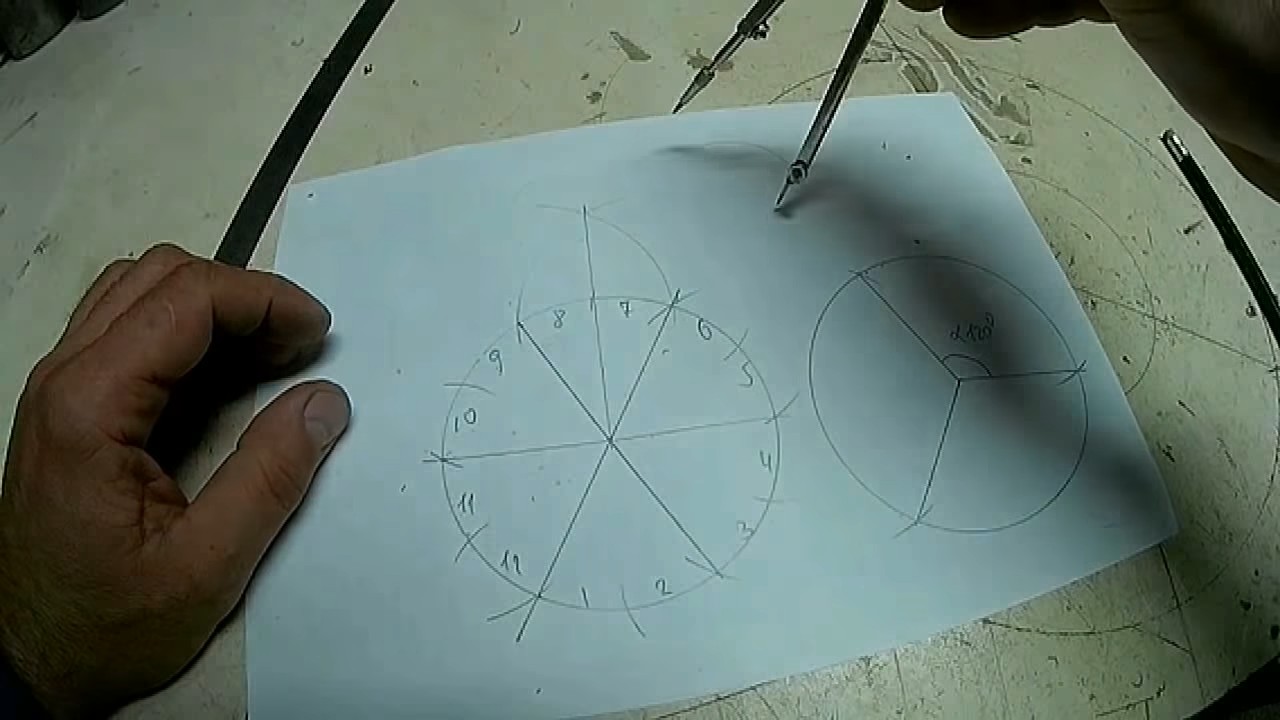
Выполняется следующим образом. Проводим горизонтальную и вертикальную взаимно перпендикулярные оси окружности. Из верхней точки «1» окружности проводим под произвольным углом к вертикальной оси прямую линию. На ней откладываем равные отрезки произвольной длины, число которых равно числу частей на которое мы делим данную окружность, например 9. Конец последнего отрезка соединяем с нижней точкой вертикального диаметра. Проводим линии, параллельные полученной, из концов отложенных отрезков до пересечения с вертикальным диаметром, разделив таким образом вертикальный диаметр данной окружности на заданное количество частей. Радиусом равным диаметру окружности, из нижней точки вертикальной оси проводим дугу MN до пересечения с продолжением горизонтальной оси окружности. Из точек M и N проводим лучи через чётные ( или нечётные) точки деления вертикального диаметра до пересечения с окружностью. Полученные отрезки окружности будут являться искомыми, т.к. точки 1, 2, …. 9 делят окружность на 9-ть ( N ) равных частей.
Нахождение центра дуги окружности
Для нахождения центра дуги окружности нужно выполнить следующие построения: на данной дуге отмечаем четыре произвольные точки А, В, С, D и соединяем их попарно хордами АВ и СD. Каждую из хорд при помощи циркуля делим пополам, получив, таким образом, перпендикуляр, проходящий через середину соответствующей хорды. Взаимное пересечение этих перпендикуляров даёт центр данной дуги и соответствующей ей окружности.
Как посчитать длину окружности
Онлайн калькулятор
Как посчитать длину окружности зная диаметр
Какая длина у окружности если
Какова длина окружности (С) если её диаметр d?
Формула
С = π⋅d , где π ≈ 3.14
Пример
Если диаметр круга равен 1 см, то его длина примерно равна 3.14 см.
Как посчитать длину окружности зная радиус
Какая длина у окружности если
Какова длина окружности (С) если её радиус r?
Формула
С = 2⋅π⋅r , где π ≈ 3.14
Пример
Если радиус круга равен 0.5 см, то его длина примерно равна 3.14 см.
Как посчитать длину окружности зная её площадь
Какая длина у окружности если
Какова длина окружности (С) если её площадь S?
Формула
С = 2π⋅ √ S /π , где π ≈ 3.14
Пример
Если площадь круга равна 6 см 2 , то его длина примерно равна 8.68 см.
Площадь круга и его частей. Длина окружности и ее дуг
Основные определения и свойства
Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки — центра окружности
Часть окружности, расположенная между двумя точками окружности
Конечная часть плоскости, ограниченная окружностью
Часть круга, ограниченная двумя радиусами
Часть круга, ограниченная хордой
Выпуклый многоугольник, у которого все стороны равны и все углы равны
Около любого правильного многоугольника можно описать окружность
| Фигура | Рисунок | Определения и свойства |
| Окружность |  |
|
| Дуга |  |
|
| Круг |  |
|
| Сектор |  |
|
| Сегмент |  |
|
| Правильный многоугольник |  |
|
 |
| Окружность |
 |
Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки — центра окружности
Дуга
Часть окружности, расположенная между двумя точками окружности
Круг
Конечная часть плоскости, ограниченная окружностью
Сектор
Часть круга, ограниченная двумя радиусами
Сегмент
Часть круга, ограниченная хордой
Правильный многоугольник
Выпуклый многоугольник, у которого все стороны равны и все углы равны
Около любого правильного многоугольника можно описать окружность
Определение 1 . Площадью круга называют предел, к которому стремятся площади правильных многоугольников, вписанных в круг, при неограниченном возрастании числа сторон.
Определение 2 . Длиной окружности называют предел, к которому стремятся периметры правильных многоугольников, вписанных в круг, при неограниченном возрастании числа сторон.
Замечание 1 . Доказательство того, что пределы площадей и периметров правильных многоугольников, вписанных в круг, при неограниченном возрастании числа сторон действительно существуют, выходит за рамки школьной математики и в нашем справочнике не приводится.
Определение 3 . Числом π (пи) называют число, равное площади круга радиуса 1.
Замечание 2 . Число π является иррациональным числом, т.е. числом, которое выражается бесконечной непериодической десятичной дробью:
Число π является трансцендентным числом, то есть числом, которое не может быть корнем алгебраического уравнения с целочисленными коэффициентами.
Формулы для площади круга и его частей

где R – радиус круга, D – диаметр круга

если величина угла α выражена в радианах

если величина угла α выражена в градусах

если величина угла α выражена в радианах

если величина угла α выражена в градусах
| Числовая характеристика | Рисунок | Формула |
| Площадь круга |  |
|
| Площадь сектора |  |
|
| Площадь сегмента |  |
| Площадь круга |
 |

где R – радиус круга, D – диаметр круга
Площадь сектора

если величина угла α выражена в радианах

если величина угла α выражена в градусах
Площадь сегмента

если величина угла α выражена в радианах

если величина угла α выражена в градусах
Формулы для длины окружности и её дуг
где R – радиус круга, D – диаметр круга
если величина угла α выражена в радианах

если величина угла α выражена в градусах
| Длина окружности |
 |
где R – радиус круга, D – диаметр круга
Длина дуги
если величина угла α выражена в радианах

если величина угла α выражена в градусах
Площадь круга
Рассмотрим две окружности с общим центром ( концентрические окружности ) и радиусами радиусами 1 и R , в каждую из которых вписан правильный n – угольник (рис. 1).
Обозначим через O общий центр этих окружностей. Пусть внутренняя окружность имеет радиус 1 .
Поскольку при увеличении n площадь правильного n – угольника, вписанного в окружность радиуса 1 , стремится к π , то при увеличении n площадь правильного n – угольника, вписанного в окружность радиуса R , стремится к числу πR 2 .
Таким образом, площадь круга радиуса R , обозначаемая S , равна
Длина окружности
то, обозначая длину окружности радиуса R буквой C , мы, в соответствии с определением 2, при увеличении n получаем равенство:
откуда вытекает формула для длины окружности радиуса R :
Следствие . Длина окружности радиуса 1 равна 2π.
Длина дуги
Рассмотрим дугу окружности, изображённую на рисунке 3, и обозначим её длину символом L(α), где буквой α обозначена величина соответствующего центрального угла.
В случае, когда величина α выражена в градусах, справедлива пропорция
из которой вытекает равенство:
В случае, когда величина α выражена в радианах, справедлива пропорция
из которой вытекает равенство:
Площадь сектора
Рассмотрим круговой сектор, изображённый на рисунке 4, и обозначим его площадь символом S (α) , где буквой α обозначена величина соответствующего центрального угла.
В случае, когда величина α выражена в градусах, справедлива пропорция
из которой вытекает равенство:
В случае, когда величина α выражена в радианах, справедлива пропорция
из которой вытекает равенство:
Площадь сегмента
Рассмотрим круговой сегмент, изображённый на рисунке 5, и обозначим его площадь символом S (α), где буквой α обозначена величина соответствующего центрального угла.
Поскольку площадь сегмента равна разности площадей кругового сектора MON и треугольника MON (рис.5), то в случае, когда величина α выражена в градусах, получаем
В случае, когда величина α выражена в в радианах, получаем
http://poschitat.online/dlina-okruzhnosti
http://www.resolventa.ru/demo/diaggia6.htm
Хоть деление круга на несколько равных частей входит в школьную программу, но со временем основы забываются. А строителям, сантехникам, жестянщикам и другим представителям рабочих специальностей эти знания необходимы. Рассмотрим, как разделить круг на 3, 6 и 12 частей.
Диаметр круга не имеет значения. Если нужен очень большой размер – вместо циркуля используют веревку и карандаш.
Деление на 3 части
Шаг 1 из 7
Чертим произвольный круг.
Шаг 2 из 7
Радиус окружности делит ее на 6 равных частей. Поэтому выбираем любую позицию на периметре круга, устанавливаем острие циркуля и находим с двух сторон от нее точки, расстояние до которых равно радиусу.
Шаг 3 из 7
Затем грифель оставляем на одной из этих точек, а острие перемещаем на такую же длину.
Шаг 4 из 7
С этой позиции определяем следующую точку.
Шаг 5 из 7
На окружности получится 3 засечки.
Шаг 6 из 7
Соединяем засечки с центральной точкой фигуры.
Шаг 7 из 7
Каждая из трех частей имеет внутренний угол 120°.
Деление на 6 частей
Шаг 1 из 3
Для деления на 6 частей делаем засечки на окружности, не через одну позицию, а последовательно.
Шаг 2 из 3
Получаем 6 точек на окружности.
Шаг 3 из 3
Соединяем точки с центром и параллельной засечкой и получаем 6 частей.
Деление на 12 частей: 1 способ
Шаг 1 из 6
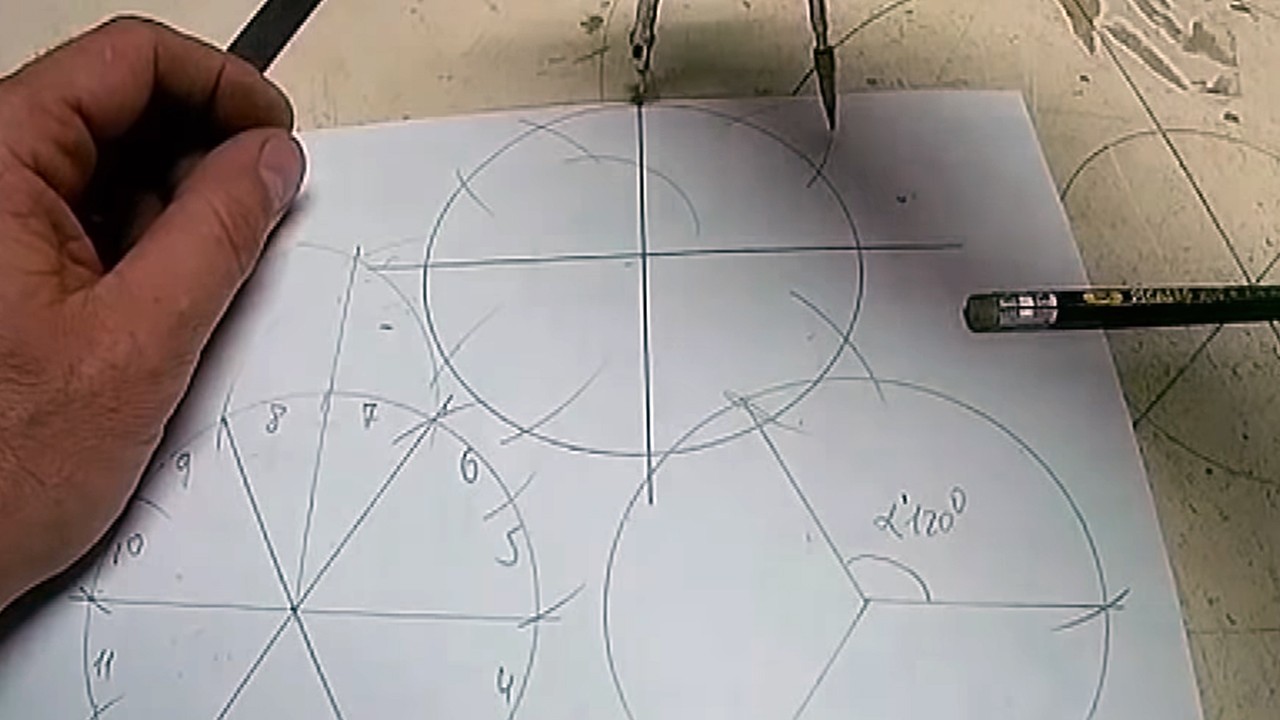
Чтобы разбить на 12 есть, как минимум, 2 способа. Первый способ – расчеты проводятся из круга, деленного на 6 частей.
Для этого из двух ближайших точек окружности проводим 2 дуги за пределы фигуры, навстречу друг другу.
Шаг 2 из 6
Точку пересечения дуг соединяем с центральной точкой окружности.
Шаг 3 из 6
Так мы делим 1/6 на 2 части.
Шаг 4 из 6
Циркулем измеряем длину получившегося сегмента.
Шаг 5 из 6
Эту длину откладываем на других частях.
Шаг 6 из 6
Затем новые засечки соединяем прямыми с центром, получаем деление на 12 частей.
Деление на 12 частей: 2 способ
Шаг 1 из 2
Второй способ – рисуем 2 перпендикулярные прямые через центр окружности, тем самым делим ее на 4 сегмента.
Шаг 2 из 2
От каждой точки пересечения прямой и окружности в 2 стороны отмеряем расстояние, равное радиусу, намечаем. Так мы получаем снова 12 частей.
|
haleron 5 лет назад
Alexsandr82 4 года назад 1/6 часть чего либо предполагает, что это что-то было разделено на шесть одинаковых между собой частей, т.е. все части равны между собой. И вот одна такая часть и есть 1/6 часть. Проще всего найти 1/6 часть от какого нибудь числа, для этого нужно это число просто разделить на 6, например 1/6 часть от 66 будет равна 11. Также можно представить 1/6 часть в виде процентов, для этого нужно единицу разделить на 6 и умножить на 100%, в результате мы получим примерно 16,7%. Сложнее найти 1/6 часть от геометрических фигур, особенно если нам не известны их размеры а решение возможно лишь графическое, причем найти 1/6 часть круга, прямоугольника или квадрата относительно просто, сложнее искать 1/6 неправильных фигур, косоугольных треугольников и многоугольников. Практически невозможно найти одну шестую часть геометрически сложных объектов, например зданий, статуй и тому подобное. Хотя теоретически мы можем расчитать 1/6 часть статуи по ее весу или объему но вот практически отделить от статуи или здания 1/6 практически невозможно. система выбрала этот ответ лучшим комментировать
в избранное
ссылка
отблагодарить ЧипИДейл 4 года назад «1/6» — так обозначается простая правильная дробь, которая обозначает одну шестую часть от чего-либо целого. Для примера 1/6 часть:
Наглядно показать 1/6 (одну шестую) часть удобно на круглом циферблате часов. Надо весь циферблат разделить на одинаковые сектора. Получится каждый сектор по 10 минут. Вот такой один сектор и будет равен 1/6 части от полного круга. Аналогично два сектора составят 2/6 части (или 1/3); три сектора — 3/6 части (или 1/2, или полчаса) и так далее. Для наглядности публикую картинку с разделенным на 6 частей циферблатом. комментировать
в избранное
ссылка
отблагодарить RIOLIt 5 лет назад Это- пи/3 радиан- шестьдесят градусов, одна шестая часть окружности, 16, 7% чего- либо комментировать
в избранное
ссылка
отблагодарить Galina7v7 5 лет назад 1/6 часть суток это 4 часа.1/6 часть километра это 166,66666 метров.Километр пробежать некоторым сложновато, а 166 метров только начать.А 1/6 часть метра это длина ладони.И так во всём, дели на шесть то от чего шестая часть и получишь ответ на вопрос.А 1/6 часть часа 10 минуток, а та же часть минутки 10 секунд. То есть 1/6 часть длины, веса, времени, объёма и всего того, что можно разделить на 6 частей, это в шесть раз меньше того, что делим. комментировать
в избранное
ссылка
отблагодарить Юрий добрый 5 лет назад Перете объект и делите на 6 частей. Вот это и будет ода шестая. Также одна вторая. Это 1 объект поделён на 2 части. комментировать
в избранное
ссылка
отблагодарить Знаете ответ? |
Download Article
Download Article
There are a number of different ways to divide circle into equal parts. If you are using a pencil and paper, you will need a compass to divide the circle accurately into six equal pieces. If you need to divide the circle for graphic design purposes, you may want to use Adobe Illustrator or InDesign. Although these programs are similar, the methods to divide the circle are unique to each program.
-
1
Draw a circle with the compass. Align the pencil tip with the tip of the needle. Place the point of the compass down on the paper. Set the distance between the pencil and needle equal to the radius of the circle that you would like and draw. Swing the compass around 360° to complete the circle.[1]
- Make sure the hinge is tight so it doesn’t slip while drawing.
- Also make sure the pencil is securely in its holder so it also doesn’t move while drawing.
- This first circle is the main circle that you will be dividing.
-
2
Draw a second circle whose center is the edge of the first circle. Place the needle of the compass at any point along the edge of the main circle. Keep the distance between the needle and pencil the same as the first circle. Swing the compass around to complete the second circle.[2]
- The second circle should overlap with the first circle and the edge should cross through the center of the first circle.
- If the distance between the needle and the pencil changes at all, the circle will not be divided equally.
Advertisement
-
3
Use the intersection of the first and second circle to draw a third circle. Place the needle at the intersection of the first and second circle. There are two intersections and you can use either one; this will be the center of a third circle. Use the compass to complete the third circle.[3]
- Again, keep the compass at the same distance for every circle you draw.
- At this point you should have three overlapping circles. You should notice that the two outer circles overlap with the center of the first main circle.
-
4
Draw a fourth circle using the intersection of the main circle and the third circle. Just as you did to draw the second and third circle, use the intersection of the third circle with the main circle as the center point. Remember, going clockwise around the circle, you will use the intersection to the left of the circle. Place the compass on that intersection and draw a fourth circle.[4]
- You are halfway done with drawing circles.
-
5
Draw three more circles using the next intersection of each circle. Using the intersection of the previously drawn circle with the main circle as the center, draw the next circle. Continue the next three circles until you have a total of six circles all around the main circle.[5]
- The inside of your original circle should now look like a 6 petaled flower.
-
6
Use a ruler to draw a straight line through the center of the circle. This is the first of three lines you will need to draw to divide the circle into 6 parts. Every line, including this one, should cross the exact center of the circle and divide two of the six inner «flower petals» of your drawing in half.
-
7
Draw another straight line one flower petal (or 60 degrees) clockwise from the first. This line will bisect two opposite flower petals and will go through the exact center of the circle.[6]
-
8
Draw your final straight line one more flower petal (or 60 degrees) clockwise from the last. You now have a circle divided into 6 equal parts.
Advertisement
-
1
Draw a line through the center of the circle. The first step to dividing the circle is cutting it directly in half. Choose a point anywhere along the circle and draw a line through the center of the circle to the opposite end. The circle is now divided into two equal pieces.
- This method works well if you are trying to cut a pie or a cake.
-
2
Draw two more lines that divide one half of the circle into thirds. Next, you want to draw two lines that cut the half into thirds. You can approximate this by dividing one half of the cake into three equal pieces.[7]
- Get as close to three equal pieces as possible. Again, this method is just an approximation.
-
3
Extend those lines into the other half of the circle. Continue both of those lines through the center of the circle to the opposite side of the circle. If done correctly, the circle should now be divided into six approximately equal parts.
- This method is not exact, but is an easy way to divide the circle into six equal parts by eye.
Advertisement
-
1
Launch Adobe Illustrator. If you have a shortcut on your desktop, you can open the application by double-clicking on this icon. If you don’t have a shortcut, use the start menu or search for the application and open it from the search bar.
-
2
Locate the Polar Grid tool. The Polar Grid tool is one of the options in the toolbar on the left side of your screen. It is under the Line Segment group of tools. It kind of looks like a spider web; it is a circle with divided lines through it.
- To see the tools nested underneath the Line Segment, click and hold on the Line Segment tool until a window opens with more options.
- Click on the Polar Grid tool to activate it.
-
3
Click and drag to create a circle. With the Polar Grid tool active, click on the canvas and drag the mouse to create the circle. You should see a circle appear that likely has smaller concentric circles within it. These can be removed later.
- While dragging, adjust the size of the circle by dragging in and out until you reach the desired size.
- Hold ⇧ Shift to snap to a perfect circle.
- Keep holding ⇧ Shift and don’t release the mouse click until you finish the next step.
-
4
Separate into parts using the arrow keys. While dragging the circle, press on the right arrow key until you see that the circle has been divided into 6 equal parts. If you accidentally press the key too many times, simply push the left arrow key to decrease the number of divisions.
- When the circle is the size you want and divided into 6 equal parts, you can let go of the mouse.
- If you let go of the mouse too early, there is an alternative method: Keep the Polar Grid tool active (don’t click back to the black arrow) and click on any whitespace in your document. An options menu will pop up and you can set the number of divisions to 6 and remove the concentric dividers by setting that option to 0.
Advertisement
-
1
Locate the Ellipse tool and create a circle. The Ellipse tool is part of the toolbar on the left side of the screen. It is a shaded ellipse. Hold down ⇧ Shift and click on the white canvas, and drag the circle to the size that you want.
- Release the click on the mouse and then release ⇧ Shift to make a perfect circle.
-
2
Place both vertical and horizontal guides through the center of the circle. To place a vertical guide, click on the vertical ruler and drag right towards the circle. Place the guide over the vertical center points of the circle. To place the horizontal guide, click on the horizontal ruler and drag down toward the circle.[8]
- If the guides don’t get properly placed the first time, you can click on them again and drag them into place.
-
3
Locate the Polygon Frame tool. The Polygon Frame tool is located in the left toolbar underneath the Rectangle Frame tool group.[9]
Click and hold on the Rectangle Frame tool to reveal the icons underneath. The tool looks like a hexagon with an “X” through it.- Click on the Polygon Frame tool to make it active.
- It will now be the icon showing on the toolbar.
-
4
Draw an equilateral triangle with the Polygon Frame tool. With the Polygon Frame tool selected, click onto the white canvas to open the options dialog box. Set the number of sides to 3 and click okay.[10]
With ⇧ Shift held down, click and drag a triangle that is slightly longer than the radius of your circle.- Don’t release ⇧ Shift until after you let go of the mouse click. This will ensure that you have made a perfect equilateral triangle.
-
5
Align the triangle with the center of the circle. Make sure the black arrow is selected on toolbar and click on the triangle. Drag it to the center of the circle so that the bottom-left corner snaps to the center of the circle.
- The right side of the triangle should hang outside the circle with the bottom and left side of the triangle intersecting the circle.
-
6
Join the circle and the triangle into a wedge with the Intersect tool. Highlight both the triangle and the circle. With both highlighted, find the Intersect tool nested under Object>Pathfinder. After clicking Intersect, the circle should disappear and a wedge shape should appear.
- This wedge is one-sixth of the circle.
-
7
Copy and rotate the wedge 60°. Highlight the wedge and right click. Click on Transform>Rotate. Set the angle to 60° and click Copy. Once you click copy, a second wedge, rotated 60° from the original wedge, will appear.
- Align this second wedge next to the first wedge. You will start to see the circle forming.
-
8
Repeat the rotate and copy process until you have 6 wedges. Using the second wedge you just made, right click again and rotate and copy the second wedge. This will form a third wedge that you can place next to the second. Repeat this with the third, fourth, and fifth wedge until you have six total wedges.
- Align each wedge next to the previous one until you have a perfect circle divided into 6 equal parts.
Advertisement
Add New Question
-
Question
How do I divide a circle into 4 equal parts using a set square?
First you have to find and mark the exact center of the circle. Then draw a straight line from one side of the circle through the center to the other side of the circle. That’s a diameter. Finally, use the set square to draw another diameter perpendicular to the first diameter. You have now divided the circle into four equal quadrants.
-
Question
How can I divide a circle into nine equal parts?
Draw a radius. Then, using a protractor, draw eight more radii, each 40° from the nearest radius.
-
Question
How can I divide a circle into seven equal parts?
360° ÷ 7 = 51.43°. Use a protractor to draw eight radii, each approximately 51.43° from each other.
See more answers
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
Video
Thanks for submitting a tip for review!
References
About This Article
Article SummaryX
To divide a circle into 6 equal parts, start by drawing a line through the center of the circle starting on a point anywhere along the edge and ending at the opposite edge. Next, draw two more lines that divide half of the circle into three parts, making sure that the sections are as equal as possible. Then, extend those two lines into the other half of the circle to the opposite edges to create 6 wedge shapes. For tips on dividing a circle into equal parts using a compass, read on!
Did this summary help you?
Thanks to all authors for creating a page that has been read 198,291 times.
Did this article help you?

Круговой сегмент — часть круга ограниченная дугой и секущей (хордой).
На рисунке:
L — длина дуги сегмента
c — хорда
R — радиус
a — угол сегмента
h — высота
Первый калькулятор рассчитывает параметры сегмента, если известен радиус и угол по следующим формулам:
Формулы вычисления параметров сегмента
Площадь сегмента:
[1]
Длина дуги:
Длина хорды:
Высота сегмента:
Сегмент
Угол в градусах, образуемый радиусами сектора
Точность вычисления
Знаков после запятой: 2
Однако, как справедливо заметил наш пользователь:«на практике часто случается, что как радиус дуги, так и угол неизвестны» (см. длина дуги ). Для этого случая для расчета площади сегмента и длины дуги можно использовать следующий калькулятор:
Параметры сегмента по хорде и высоте
Точность вычисления
Знаков после запятой: 2
Калькулятор вычисляет радиус круга по длине хорды и высоте сегмента по следующей формуле:
Далее, зная радиус и длину хорды, легко найти угол сегмента по формуле:
Остальные параметры сегмента вычисляются аналогично первому калькулятору, по формулам, приведенным в начале статьи.
Следующий калькулятор вычисляет площадь сегмента по высоте и радиусу:
Площадь сегмента круга по радиусу и высоте
Точность вычисления
Знаков после запятой: 2
Этот калькулятор вычисляет угол из высоты и радиуса по следующей формуле:
далее используется формула [1] для получения площади.
15 вычислений по сегменту круга в одной программе
Последний калькулятор включает в себя все оставшиеся вычисления параметров кругового сегмента:
- длина дуги
- угол
- хорда
- высота
- радиус
- площадь
Выберите два известных аргумента и калькулятор выдаст вам все оставшиеся.
Круговой сегмент — все варианты расчета
Точность вычисления
Знаков после запятой: 2
Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.