Две фигуры называют равными, если одну их них можно так наложить на другую,
что эти фигуры совпадут.
Площади равных фигур равны. Их периметры тоже равны.
Площадь квадрата
Запомните!
Для вычисления площади квадрата нужно умножить его длину на саму себя.
S = a · a
Пример:
SEKFM = EK · EK
SEKFM = 3 · 3 = 9 см2
Формулу площади квадрата, зная
определение степени,
можно записать следующим образом:
S = a2
Площадь прямоугольника
Запомните!
Для вычисления площади прямоугольника нужно умножить его длину на ширину.
S = a · b
Пример:
SABCD = AB · BC
SABCD = 3 · 7 = 21 см2
Запомните!
Нельзя вычислять периметр или площадь, если длина и ширина выражены в разных единицах длины.
Обязательно проверяйте, чтобы и длина, и ширина были выражены в одинаковых единицах, то есть обе в см, м и т.д.
Площадь сложных фигур
Запомните!
Площадь всей фигуры равна сумме площадей её частей.
Задача: найти площадь огородного участка.
Так как фигура на рисунке не является ни квадратом, ни прямоугольником, рассчитать её площадь можно используя
правило выше.
Разделим фигуру на два прямоугольника, чьи площади мы можем легко рассчитать по известной формуле.
SABCE = AB · BC
SEFKL = 10 · 3 = 30 м2
SCDEF = FC · CD
SCDEF = 7 · 5 = 35 м2
Чтобы найти площадь всей фигуры, сложим площади найденных прямоугольников.
S = SABCE + SEFKL
S = 30 + 35 = 65 м2
Ответ: S = 65 м2 — площадь огородного участка.
Свойство ниже может вам пригодиться при решении задач на площадь.
Запомните!
Диагональ прямоугольника делит прямоугольник на два равных треугольника.
Площадь любого из этих треугольников равна половине площади прямоугольника.
Рассмотрим прямоугольник:
АС — диагональ прямоугольника
ABCD. Найдём площадь треугольников
ABC и

Вначале найдём площадь прямоугольника по формуле.
SABCD = AB · BC
SABCD = 5 · 4 = 20 см2
S
ABC = SABCD : 2
S
ABC = 20 : 2 = 10 см2
S
ABC =
S
ACD = 10 см2
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
3 декабря 2015 в 22:54
Ирина Петренко
Профиль
Благодарили: 0
Сообщений: 1
Ирина Петренко
Профиль
Благодарили: 0
Сообщений: 1
как написать правильно площадь треугольника?
0
Спасибо
Ответить
9 декабря 2015 в 19:41
Ответ для Ирина Петренко
Тима Клюев
Профиль
Благодарили: 0
Сообщений: 8
Тима Клюев
Профиль
Благодарили: 0
Сообщений: 8
S(рисуешь мини треугольник) = ,,,,,
0
Спасибо
Ответить
Все формулы по геометрии. Площади фигур
Чтобы решать задачи по геометрии, надо знать формулы — такие, как площадь треугольника или площадь параллелограмма — а также простые приёмы, о которых мы расскажем.
Начнем с квадрата.
Площадь квадрата равна квадрату его стороны.
Площадь прямоугольника равна произведению его длины и ширины.
Площадь параллелограмма равна произведению его стороны на высоту, проведенную к этой стороне. Она также равна произведению его сторон на синус угла между ними.
Для площади треугольника есть целых 5 формул. И все они применяются в задачах ЕГЭ.
1) Площадь треугольника равна половине произведения его стороны на высоту, проведенную к этой стороне:
2) Она также равна половине произведения его сторон на синус угла между ними:
3) По формуле Герона, где
полупериметр.
4) Также площадь треугольника равна произведению его полупериметра на радис вписанной окружности, S = pr.
5) Еще один способ. Площадь треугольника равна произведению его сторон, деленному на 4 радиуса описанной окружности,
Есть и другие формулы для площади треугольника. Но для решения заданий ЕГЭ, и первой, и второй части, достаточно этих пяти.
Площадь прямоугольного треугольника равна половине произведения его катетов. Она также равна половине произведения гипотенузы на высоту, проведенную к этой гипотенузе:
Площадь правильного треугольника равна квадрату его стороны, умноженному на и деленному на 4:
Площадь трапеции равна произведению полусуммы оснований на высоту,
Также можно сказать, что площадь трапеции равна произведению ее средней линии на высоту,
Площадь произвольного четырехугольника равна половине произведения его диагоналей на синус угла между ними,
Площадь ромба равна произведению квадрата его стороны на синус угла ромба. Она также равна половине произведения диагоналей:
Площадь круга равна произведению числа и квадрата радиуса круга.
Ее также можно записать как произведение числа и квадрата диаметра круга, деленного на 4:
Вспомним важные свойства площадей фигур.
- Равные фигуры имеют равные площади.
Иногда фигуры, имеющие равные площади, еще называют равновеликими. - Если фигура составлена из нескольких фигур, не имеющих общих внутренних точек, то ее площадь равна сумме площадей этих фигур.
Пример. Найдем площадь фигуры, изображенной на клетчатой бумаге с размером клетки 1см1см.
Решение:
Найдем площадь фигуры на рисунке как сумму площадей нескольких фигур.
На рисунке это три треугольника и трапеция, указаны их площади. Тогда площадь фигуры равна 10 + 3,5 + 1,5 + 3 = 18.
Ответ: 18.
3. Отношение площадей подобных фигур равно квадрату коэффициента подобия.
Треугольники АВС и на рисунке называются подобными.
У треугольника все стороны в k раз длиннее, чем у треугольника АВС. Высота треугольника
в k раз длиннее, чем высота треугольника АВС. Тогда площадь треугольника
в
раз больше, чем площадь треугольника АВС.
4. На рисунке показаны треугольники АВС и BCD, имеющие общую высоту. Отношение площадей этих треугольников равно отношению АС к CD:
5. Треугольники АВС и АЕС на рисунке имеют одинаковое основание и разные высоты.
Отношение площадей этих треугольников равно отношению их высот:
6. Медиана треугольника делит его на два равновеликих, то есть равных по площади, треугольника.
На рисунке СМ — медиана треугольника АВС. Площади треугольников АСМ и ВСМ равны.
7. Три медианы треугольника делят его на шесть равных по площади треугольников.
На рисунке все 6 треугольников, из которых состоит треугольник АВС, имеют равные лощади.
Задачи ЕГЭ и ОГЭ по теме: Площади фигур.
Задача 1. Найдите площадь треугольника, две стороны которого равны 8 и 12, а угол между ними равен
Решение:
Площадь треугольника равна половине произведения его сторон на синус угла между ними. Поэтому
Ответ: 24.
Задача 2. Площадь треугольника ABC равна 4, DE — средняя линия, параллельная стороне AB. Найдите площадь треугольника CDE.
Решение:
Так как DE и АВ параллельны, треугольники CDE и САВ подобны с коэффициентом подобия Площади подобных фигур относятся как квадрат коэффициента подобия. Тогда
Ответ: 1.
Задача 3. У треугольника со сторонами 9 и 6 проведены высоты к этим сторонам. Высота, проведенная к первой стороне, равна 4. Чему равна высота, проведенная ко второй стороне?
Решение:
Выразим площадь двумя способами:
Тогда
Ответ: 6.
Задача 4. Площадь треугольника ABC равна 10, DE — средняя линия, параллельная стороне AB. Найдите площадь трапеции ABED.
Решение:
Треугольник CDE подобен треугольнику CAB с коэффициентом Площади подобных фигур относятся как квадрат коэффициента подобия, поэтому
Следовательно, 
Ответ: 7,5.
Задача 5. В параллелограмме ABCD AB = 3, AD = 21, . Найдите большую высоту параллелограмма.
Решение:
Большая высота — это DH, потому что проведена к меньшей стороне. Из треугольника АDН:
Ответ: 18.
Задача 6. Найдите площадь квадрата, если его диагональ равна 1.
Решение:
Квадрат — это частный случай ромба. Площадь квадрата равна половине произведения его диагоналей. Поэтому она равна 0,5.
Ответ: 0,5.
Задача 7. Найдите периметр прямоугольника, если его площадь равна 18, а отношение соседних сторон равно 1:2.
Решение:
Площадь прямоугольника равна произведению его длины на ширину. Периметр прямоугольника равен сумме длин всех сторон. Пусть одна из сторон прямоугольника равна a, тогда вторая равна 2a. Площадь прямоугольника равна тогда одна из сторон равна 3, а другая 6. Периметр P = 2 · 3 + 2 · 6 = 18.
Ответ: 18.
Задача 8. Параллелограмм и прямоугольник имеют одинаковые стороны. Найдите острый угол параллелограмма, если его площадь равна половине площади прямоугольника. Ответ дайте в градусах.
Решение:
Площадь параллелограмма равна произведению его сторон на синус угла между ними. Площадь прямоугольника равна произведению длины на ширину. Пусть одна сторона параллелограмма и прямоугольника равна вторая равна
а острый угол параллелограмма равен
Тогда площадь параллелограмма равна
а площадь прямоугольника равна
По условию площадь прямоугольника вдвое больше:
Следовательно,
Ответ: 30.
Задача 9. Площадь параллелограмма равна 40, две его стороны равны 5 и 10. Найдите большую высоту этого параллелограмма.
Решение:
Площадь параллелограмма равна произведению его основания на высоту, проведенную к этому основанию. Пусть высоты равны соответственно a и b. Тогда S = 5 · a = 10 · b = 40. Поэтому a = 8, b = 4. Большая высота равна 8.
Ответ: 8.
Задача 10. Найдите площадь ромба, если его высота равна 2, а острый угол 30
Решение:
Площадь ромба равна произведению квадрата его стороны на синус угла ромба. С другой стороны, площадь ромба равна произведению его основания на высоту, проведенную к этому основанию. Пусть сторона ромба равна
Получим уравнение:
Корень уравнения a = 4, поэтому
Ответ: 8.
Задача 11. Найдите площадь ромба, если его диагонали равны 4 и 12.
Решение:
Площадь ромба равна половине произведения его диагоналей.
Ответ: 24.
Задача 12. Основания равнобедренной трапеции равны 14 и 26, а ее периметр равен 60. Найдите площадь трапеции.
Решение:
Трапеция равнобедренная, значит,
Тогда по теореме Пифагора из треугольника ADH:
Ответ: 160.
Задача 13. Найдите площадь прямоугольной трапеции, основания которой равны 6 и 2, большая боковая сторона составляет с основанием угол 45
Решение:
Проведем высоту CH. Треугольник CHB — прямоугольный, в нем
значит, он также равнобедренный, CH = HB = 4.
Ответ: 16.
Задача 14. Высота трапеции равна 5, площадь равна 75. Найдите среднюю линию трапеции.
Решение:
Средняя линия трапеции равна полусумме оснований. Выразим её из формулы площади трапеции:
Ответ: 15.
Задача 15. Основания трапеции равны 27 и 9, боковая сторона равна 8. Площадь трапеции равна 72. Найдите острый угол трапеции, прилежащий к данной боковой стороне. Ответ выразите в градусах.
Решение:
Площадь трапеции равна произведению полусуммы оснований на высоту. Пусть высота равна h, тогда
Из этого уравнения получим: h = 4.
Рассмотрим прямоугольный треугольник, гипотенузой которого является боковая сторона трапеции, равная 8, а катетом — высота трапеции. Длина катета равна половине гипотенузы, следовательно, он лежит напротив угла
Ответ: 30.
Как найти площадь нестандартной фигуры? Например, произвольного четырёхугольника? Простой приём — разобьём эту фигуру на такие, о которых мы всё знаем, и найдем её площадь — как сумму площадей этих фигур.
Задача 16. Найдем площадь четырехугольника на рисунке.
Решение:
Разделим этот четырёхугольник горизонтальной линией на два треугольника с общим основанием, равным 5. Высоты этих треугольников равны 2 и 3. Тогда площадь четырёхугольника равна сумме площадей двух треугольников:
Ответ: 12,5.
В некоторых случаях площадь фигуры можно представить как разность каких-либо площадей.
Задача 17. Найдем площадь треугольника, изображенного на клетчатой бумаге.
Не так-то просто посчитать, чему равны основание и высота в этом треугольнике! Зато мы можем сказать, что его площадь равна разности площадей квадрата со стороной 5 и трёх прямоугольных треугольников. Видите их на рисунке? Получаем:
Ответ: 10,5.
Иногда в задании надо найти площадь не всей фигуры, а её части. Обычно речь здесь идет о площади сектора — части круга.
Задача 18.
Найдите площадь сектора круга радиуса 1, длина дуги которого равна 2.
Решение:
На этом рисунке мы видим часть круга. Площадь всего круга равна так как
Остается узнать, какая часть круга изображена. Поскольку длина всей окружности равна
(так как R = 1), а длина дуги данного сектора равна 2, следовательно, длина дуги в
раз меньше, чем длина всей окружности. Угол, на который опирается эта дуга, также в
раз меньше, чем полный круг (то есть 360 градусов). Значит, и площадь сектора будет в
раз меньше, чем площадь всего круга.
Ответ: 1.
Формула Пика
Покажем, как вычислять площадь фигуры, изображенной на координатной плоскости, с помощью формулы Пика.
Задача 19. Найдите площадь многоугольника АВСDE, изображенного на рисунке.
Первый способ:
Площадь многоугольника ABCDE равна сумме площадей треугольника BCD, трапеции BKDE и треугольника AKE.
Имеем:
Второй способ — применить формулу Пика.
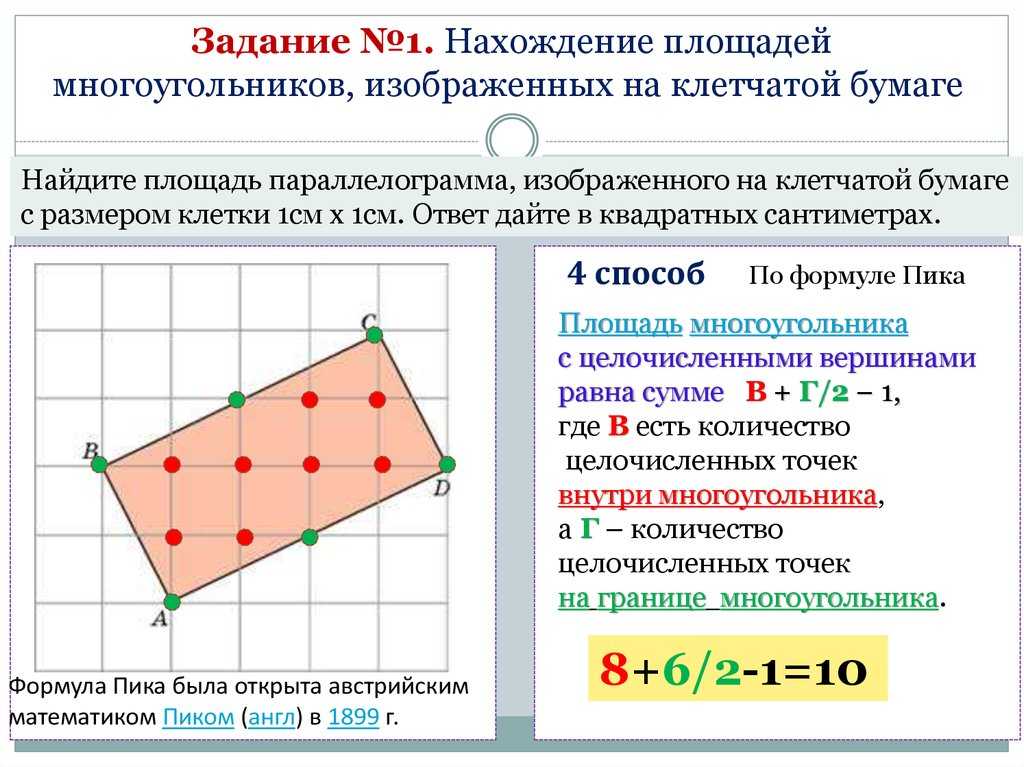
Назовем точку координатной плоскости целочисленной, если обе ее координаты — целые числа. На нашем рисунке это точки на пересечениях линий, разделяющих клетчатую бумагу на клетки.
Площадь многоугольника с целочисленными вершинами равна

Здесь В — количество целочисленных точек внутри многоугольника, Г — количество целочисленных точек на границе многоугольника.
Главное — аккуратно посчитать. На нашем рисунке
В = 24 (показаны зеленым),
Г = 8 (показаны красным),
S = 24 + — 1 = 27.
Ответ: 27.
Благодарим за то, что пользуйтесь нашими материалами.
Информация на странице «Все формулы по геометрии. Площади фигур» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.
Публикация обновлена:
08.05.2023
A combined figure is a geometrical shape that is the combination of many simple geometrical shapes.
To find the area of combined figures we will follow the steps:
Step I: First we divide the combined figure into its simple geometrical shapes.
Step II: Then calculate the area of these simple geometrical shapes separately,
Step III: Finally, to find the required area of the combined figure we need to add or subtract these areas.
Solved Examples on Area of combined figures:
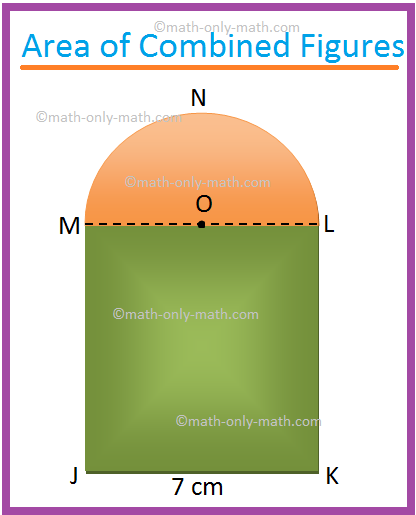
1. Find the area of the shaded region of the adjoining figure. (Use π = (frac{22}{7}))
JKLM is a square of side 7 cm. O is the centre of the
semicircle MNL.
Solution:
Step I: First we divide the combined figure into
its simple geometrical shapes.
The given combined shape is combination of a
square and a semicircle.
Step II: Then calculate the area of
these simple geometrical shapes separately.
Area of the square JKLM = 72 cm2
=
49 cm2
Area of the semicircle LNM = (frac{1}{2}) π ∙ ((frac{7}{2})^{2}) cm2 , [Since,
diameter LM = 7 cm]
=
(frac{1}{2}) ∙ (frac{22}{7}) ∙ (frac{49}{4}) cm2
=
(frac{77}{4}) cm2
=
19.25 cm2
Step III: Finally, add these areas up to get
the total area of the combined figure.
Therefore, the required area = 49 cm2 + 19.25 cm2
=
68.25 cm2.
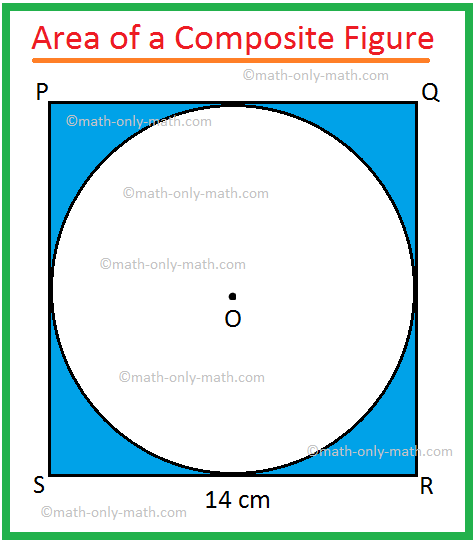
2. In the adjoining figure, PQRS is a square of side 14 cm
and O is the centre of the circle touching all sides of the square.
Find the area of the shaded region.
Solution:
Step I: First we divide the combined figure into its simple geometrical shapes.
The given combined shape is combination of a square and a circle.
Step II: Then calculate the area of these simple geometrical shapes separately.
Area of the square PQRS = 142 cm2
= 196 cm2
Area of the circle with centre O = π ∙ 72 cm2, [Since, diameter SR = 14 cm]
= (frac{22}{7}) ∙ 49 cm2
= 22 × 7 cm2
= 154 cm2
Step III: Finally, to find the required area of the combined figure we need to subtract the area of the circle from the area of the square.
Therefore, the required area = 196 cm2 — 154 cm2
= 42 cm2
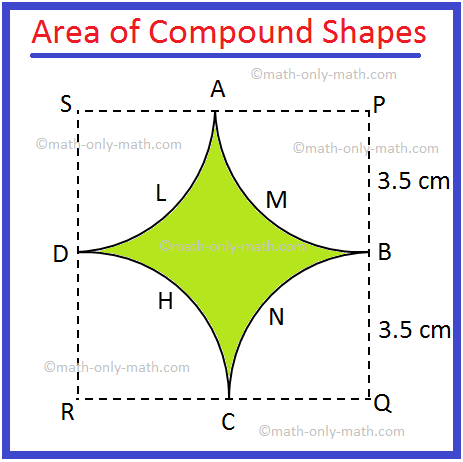
3. In the adjoining figure alongside, there are four equal quadrants of circles each of radius 3.5 cm, their centres being P, Q, R and S.
Find the area of the shaded region.
Solution:
Step I: First we divide the combined figure into its simple geometrical shapes.
The given combined shape is combination of a square and four quadrants.
Step II:Then calculate the area of these simple geometrical shapes separately.
Area of the square PQRS = 72 cm2, [Since, side of the square = 7 cm]
= 49 cm2
Area of the quadrant APB = (frac{1}{4}) π ∙ r2 cm2
= (frac{1}{4}) ∙ (frac{22}{7}) ∙ ((frac{7}{2})^{2}) cm2, [Since, side of the square = 7 cm and radius of the quadrant = (frac{7}{2}) cm]
= (frac{77}{8}) cm2
There are four quadrants and they have the same area.
So, total area of the four quadrants = 4 × (frac{77}{8}) cm2
= (frac{77}{2}) cm2
= (frac{77}{2}) cm2
Step III: Finally, to find the required area of the combined figure we need to subtract the area of the four quadrants from the area of the square.
Therefore, the required area = 49 cm2 — (frac{77}{2}) cm2
= (frac{21}{2}) cm2
= 10.5 cm2
10th Grade Math
From Areas of Combined Figures to HOME PAGE
Didn’t find what you were looking for? Or want to know more information
about Math Only Math.
Use this Google Search to find what you need.
Как найти общую площадь
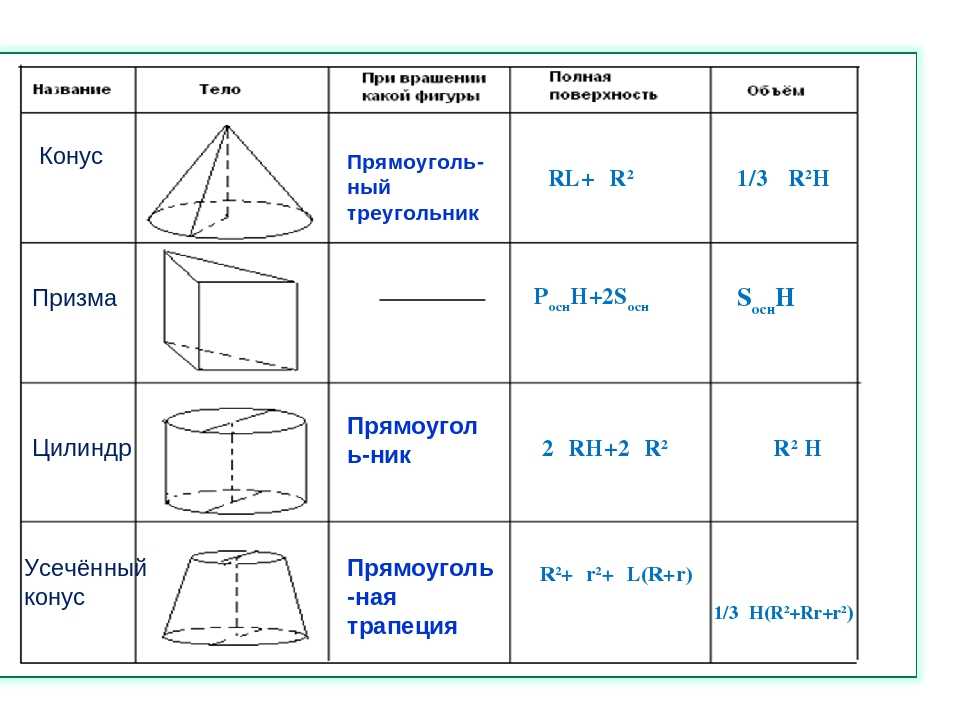
Площадью называют количественную меру плоскости, ограниченной периметром какой-либо двухмерной фигуры. Поверхность многогранников составлена не менее чем из четырех граней, каждая из которых может иметь собственную форму и размеры, а значит, и площадь. Поэтому вычисление общей площади объемных фигур с плоскими гранями не всегда простая задача.

Инструкция
Полная площадь поверхности таких многогранников как, например, призма, параллелепипед или пирамида складывается из суммы площадей граней разной величины и формы. У этих объемных фигур есть боковые поверхности и основания. Вычисляйте раздельно площади этих поверхностей, исходя из их формы и размеров, а затем суммируйте полученные значения. Например, общая площадь (S) шести граней параллелепипеда может быть найдена удвоением суммы произведений длины (a) на ширину (w), длины на высоту (h) и ширины на высоту: S = 2*(a*w + a*h + w*h).
Полная площадь поверхности правильного многогранника (S) складывается из суммы площадей каждой его грани. Так как все боковые поверхности этой объемной фигуры по определению имеют одинаковые формы и размеры, достаточно рассчитать площадь одной грани, чтобы получить возможность найти общую площадь. Если из условий задачи кроме числа боковых поверхностей (N) вам известна длина любого ребра фигуры (a) и число вершин (n) многоугольника, который образует каждую грань, сделать это можно с использованием одной из тригонометрических функций — тангенса. Найдите тангенс от угла, равного отношению 360° к удвоенному числу вершин и увеличьте результат в четыре раза: 4*tg(360°/(2*n)). Затем на полученную величину разделите произведение числа вершин на квадрат длины стороны многоугольника: n*a²/(4*tg(360°/(2*n))). Это и будет площадь каждой грани, а общую площадь поверхности многогранника рассчитайте, умножив ее на число боковых поверхностей: S = N*n*a²/(4*tg(360°/(2*n))).
В вычислениях второго шага использованы градусные меры углов, но часто вместо них применяют радианные. Тогда в формулы нужно внести поправки исходя из того, что углу в 180° соответствует количество радиан, равное числу Пи. Замените угол в 360° в формулах на величину, равную двум таким константам, и итоговая формула даже немного упростится: S = N*n*a²/(4*tg(2*π/(2*n))) = N*n*a²/(4*tg(π/n)).
Видео по теме
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Все формулы вычисления площади. Как вычислить площадь фигуры
Площади геометрических фигур — численные значения, характеризующие их размер в двумерном пространстве. Эта величина может измеряться в системных и внесистемных единицах. Так, например, внесистемная единица площади — сотка, гектар. Это в том случае, если измеряемой поверхностью является участок земли. Системная же единица площади — квадрат длины. В системе СИ принято считать, что единица площади плоской поверхности — это квадратный метр. В СГС единица площади выражается через квадратный сантиметр.
Геометрия и формулы площадей неразрывно связаны. Эта связь заключается в том, что вычисление площадей плоских фигур основывается именно на их применении. Для многих фигур выведены несколько вариантов, по которым вычисляются их квадратные размеры. Опираясь на данные из условия задачи, мы можем определить максимально простой способ для решения. Тем самым облегчить расчет и свести вероятность ошибки вычисления к минимуму. Для этого рассмотрим основные площади фигур в геометрии.
Формулы для нахождения площади любого треугольника представлены несколькими вариантами:
1) Площадь треугольника рассчитывается по основанию a и высоте h. Основанием считают сторону фигуры, на которую опущена высота. Тогда площадь треугольника:
2) Площадь прямоугольного треугольника рассчитывается точно также, если гипотенузу считать основанием. Если же за основание принять катет, то площадь прямоугольного треугольника будет равна уменьшенному вдвое произведению катетов.
На этом формулы для вычисления площади любого треугольника не заканчиваются. Другое выражение содержит стороны a,b и синусоидальную функцию угла γ, заключенного между a и b. Значение синуса находится по таблицам. Также его можно узнать с помощью калькулятора. Тогда площадь треугольника:
По данному равенству тоже можно убедиться в том, что площадь прямоугольного треугольника определяется через длины катетов. Т.к. угол γ — прямой, поэтому площадь прямоугольного треугольника рассчитывается без умножения на функцию синуса.
3) Рассмотрим частный случай — правильный треугольник, у которого сторона a известна по условию или ее длина найдется при решении. О фигуре в задаче по геометрии больше ничего не известно. Тогда площадь как найти при этом условии? В этом случае применяется формула для площади правильного треугольника:
Прямоугольник
Как найти площадь прямоугольника и использовать при этом размеры сторон, имеющих общую вершину? Выражение для вычисления такое:
Если для вычисления площади прямоугольника требуется использовать длины диагоналей, то тогда понадобится функция синуса угла, образованного при их пересечении. Такая формула площади прямоугольника имеет вид:
Квадрат
Площадь квадрата определяют как вторую степень длины стороны:
Доказательство вытекает из определения, согласно которому квадратом называют прямоугольник. У всех сторон, образующих квадрат, одинаковые размеры. Поэтому вычисление площади такого прямоугольника сводится к перемножению одной на другую, т.
е. ко второй степени стороны. И формула для вычисления площади квадрата примет искомый вид.
Площадь квадрата можно найти другим способом, например, если использовать диагональ:
Как вычислить площадь фигуры, которая образована частью плоскости, ограниченной окружностью? Для расчета площади формулы такие:
Параллелограмм
Для параллелограмма формула содержит линейные размеры стороны, высоты и математическое действие — умножение. Если же высота неизвестна, то тогда как найти площадь параллелограмма? Есть еще один способ вычисления. Потребуется определенное значение, которое примет тригонометрическая функция угла, образованного смежными сторонами, а также их длины.
Формулы площади параллелограмма таковы:
Ромб
Как найти площадь четырехугольника, называемого ромбом? Площадь ромба определяется с помощью простых математических действий с диагоналями. Доказательство опирается на тот факт, что отрезки диагоналей в d1 и d2 пересекаются под прямым углом.
Еще площадь ромба может быть найдена другим способом. Доказать это тоже нетрудно, если учесть, что стороны его одинаковы по длине. Затем подставить их произведение в похожее выражение для параллелограмма. Ведь частным случаем именно этой фигуры является ромб. Здесь γ — внутренний угол ромба. Площадь ромба определяют так:
Трапеция
Как найти площадь трапеции через основания (a и b), если в задаче указаны их длины? Здесь без известного значения длины высоты h вычислить площадь такой трапеции не удастся. Т.к. эту величину содержит выражение для вычисления:
Квадратный размер прямоугольной трапеции тоже можно вычислить таким же способом. При этом учитывают, что в прямоугольной трапеции понятия высоты и боковой стороны объединены. Поэтому для прямоугольной трапеции нужно указывать вместо высоты длину боковой стороны.
Цилиндр и параллелепипед
Рассмотрим что нужно, чтобы рассчитать поверхность всего цилиндра.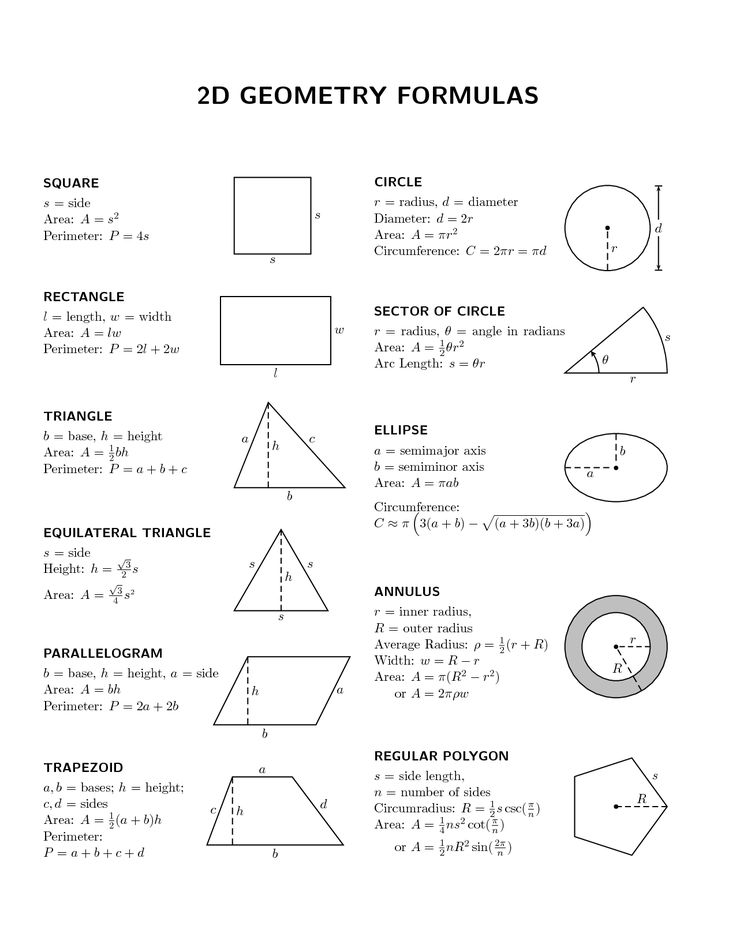
Как найти площадь параллелепипеда, который состоит из трех пар граней? Его измерения совпадают с конкретной парой. Грани, находящиеся противоположно, имеют одинаковые параметры. Сначала находят S(1), S(2), S(3) — квадратные размеры неравных граней. Затем уже площадь поверхности параллелепипеда:
Кольцо
Две окружности с общим центром образуют кольцо. Они же ограничивают площадь кольца. При этом обе расчетные формулы учитывают размеры каждой окружности. Первая из них, вычисляющая площадь кольца, содержит больший R и меньший r радиусы. Чаще их называют внешним и внутренним. Во втором выражении площадь кольца рассчитывается через больший D и меньший d диаметры. Таким образом, площадь кольца по известным радиусам рассчитывают так:
Площадь кольца, с использованием длин диаметров, определяют следующим образом:
Многоугольник
Как найти площадь многоугольника, форма которого не является правильной? Общей формулы для площади таких фигур нет.
Но если она изображена на координатной плоскости, например, это может быть клетчатая бумага, тогда как найти площадь поверхности в этом случае? Тут применяют способ, который не требует приблизительно измерить фигуру. Поступают так: если нашли точки, которые попадают в уголок клетки или имеют целые координаты, то учитывают только их. Чтобы затем выяснить, чему равна площадь, используют формулу, доказанную Пиком. Необходимо сложить количество точек, расположенных внутри ломаной линии с половиной точек, лежащих на ней, и вычесть единицу, т. е. вычисляется это таким образом:
где В,Г — количество точек, расположенных внутри и на всей ломаной линии соответственно.
Вычисление площади фигуры
– это, пожалуй, одна из наиболее сложных задач теории площадей. В школьной геометрии учат находить площади основных геометрических фигур таких как, например, треугольник, ромб, прямоугольник, трапеция, круг и т.п. Однако зачастую приходится сталкиваться с вычислением площадей более сложных фигур.
Именно при решении таких задач очень удобно использовать интегральное исчисление.
Определение.
Криволинейной трапецией
называют некоторую фигуру G, ограниченную линиями y = f(x), у = 0, х = а и х = b, причем функция f(x) непрерывна на отрезке [а; b] и не меняет на нем свой знак (рис. 1).
Площадь криволинейной трапеции можно обозначить S(G).
Определенный интеграл ʃ а b f(x)dx для функции f(x), являющийся непрерывной и неотрицательной на отрезке [а; b], и есть площадь соответствующей криволинейной трапеции.
То есть, чтобы найти площадь фигуры G, ограниченной линиями y = f(x), у = 0, х = а и х = b, необходимо вычислить определенный интеграл ʃ а b f(x)dx.
Таким образом, S(G) = ʃ а b f(x)dx.
В случае, если функция y = f(x) не положительна на [а; b], то площадь криволинейной трапеции может быть найдена по формуле
S(G) = -ʃ а b f(x)dx.
Пример 1.
Вычислить площадь фигуры, ограниченной линиями у = х 3 ; у = 1; х = 2.
Решение.
Заданные линии образуют фигуру АВС, которая показана штриховкой на рис. 2.
Искомая площадь равна разности между площадями криволинейной трапеции DACE и квадрата DABE.
Используя формулу S = ʃ а b f(x)dx = S(b) – S(a), найдем пределы интегрирования. Для этого решим систему двух уравнений:
{у = х 3 ,
{у = 1.
Таким образом, имеем х 1 = 1 – нижний предел и х = 2 – верхний предел.
Итак, S = S DACE – S DABE = ʃ 1 2 x 3 dx – 1 = x 4 /4| 1 2 – 1 = (16 – 1)/4 – 1 = 11/4 (кв. ед.).
Ответ: 11/4 кв. ед.
Пример 2.
Вычислить площадь фигуры, ограниченной линиями у = √х; у = 2; х = 9.
Решение.
Заданные линии образуют фигуру АВС, которая ограничена сверху графиком функции
у = √х, а снизу графиком функции у = 2. Полученная фигура показана штриховкой на рис. 3.
Искомая площадь равна S = ʃ а b (√x – 2). Найдем пределы интегрирования: b = 9, для нахождения а, решим систему двух уравнений:
{у = √х,
{у = 2.
Таким образом, имеем, что х = 4 = а – это нижний предел.
Итак, S = ∫ 4 9 (√x – 2)dx = ∫ 4 9 √x dx –∫ 4 9 2dx = 2/3 x√х| 4 9 – 2х| 4 9 = (18 – 16/3) – (18 – 
Ответ: S = 2 2/3 кв. ед.
Пример 3.
Вычислить площадь фигуры, ограниченной линиями у = х 3 – 4х; у = 0; х ≥ 0.
Решение.
Построим график функции у = х 3 – 4х при х ≥ 0. Для этого найдем производную у’:
y’ = 3x 2 – 4, y’ = 0 при х = ±2/√3 ≈ 1,1 – критические точки.
Если изобразить критические точки на числовой оси и расставить знаки производной, то получим, что функция убывает от нуля до 2/√3 и возрастает от 2/√3 до плюс бесконечности. Тогда х = 2/√3 – точка минимума, минимальное значение функции у min = -16/(3√3) ≈ -3.
Определим точки пересечения графика с осями координат:
если х = 0, то у = 0, а значит, А(0; 0) – точка пересечения с осью Оу;
если у = 0, то х 3 – 4х = 0 или х(х 2 – 4) = 0, или х(х – 2)(х + 2) = 0, откуда х 1 = 0, х 2 = 2, х 3 = -2 (не подходит, т.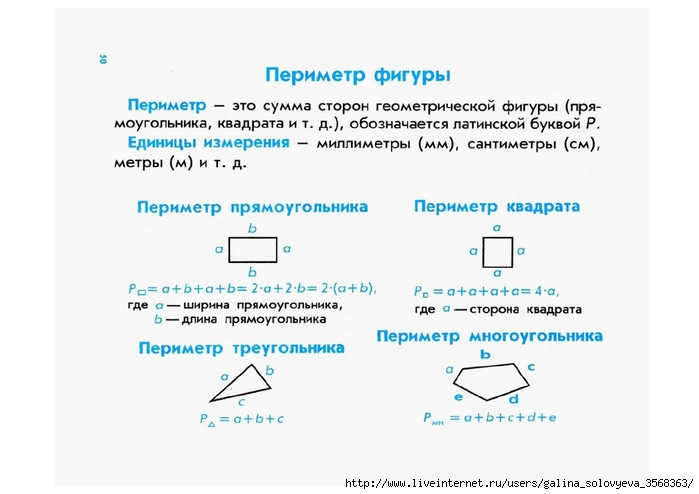
Точки А(0; 0) и В(2; 0) – точки пересечения графика с осью Ох.
Заданные линии образуют фигуру ОАВ, которая показана штриховкой на рис. 4.
Так как функция у = х 3 – 4х принимает на (0; 2) отрицательное значение, то
S = |ʃ 0 2 (x 3 – 4x)dx|.
Имеем: ʃ 0 2 (x 3 – 4х)dx =(x 4 /4 – 4х 2 /2)| 0 2 = -4, откуда S = 4 кв. ед.
Ответ: S = 4 кв. ед.
Пример 4.
Найти площадь фигуры, ограниченной параболой у = 2х 2 – 2х + 1, прямыми х = 0, у = 0 и касательной к данной параболе в точке с абсциссой х 0 = 2.
Решение.
Сначала составим уравнение касательной к параболе у = 2х 2 – 2х + 1 в точке с абсциссой х₀ = 2.
Так как производная y’ = 4x – 2, то при х 0 = 2 получим k = y’(2) = 6.
Найдем ординату точки касания: у 0 = 2 · 2 2 – 2 · 2 + 1 = 5.
Следовательно, уравнение касательной имеет вид: у – 5 = 6(х – 2) или у = 6х – 7.
Построим фигуру, ограниченную линиями:
у = 2х 2 – 2х + 1, у = 0, х = 0, у = 6х – 7.
Г у = 2х 2 – 2х + 1 – парабола. Точки пересечения с осями координат: А(0; 1) – с осью Оу; с осью Ох – нет точек пересечения, т.к. уравнение 2х 2 – 2х + 1 = 0 не имеет решений (D
x b = 2/4 = 1/2;
y b = 1/2, то есть вершина параболы точка В имеет координаты В(1/2; 1/2).
Итак, фигура, площадь которой требуется определить, показана штриховкой на рис. 5.
Имеем: S О A В D = S OABC – S ADBC .
Найдем координаты точки D из условия:
6х – 7 = 0, т.е. х = 7/6, значит DC = 2 – 7/6 = 5/6.
Площадь треугольника DBC найдем по формуле S ADBC = 1/2 · DC · BC. Таким образом,
S ADBC = 1/2 · 5/6 · 5 = 25/12 кв. ед.
S OABC = ʃ 0 2 (2x 2 – 2х + 1)dx = (2x 3 /3 – 2х 2 /2 + х)| 0 2 = 10/3 (кв. ед.).
Окончательно получим: S О A В D = S OABC – S ADBC = 10/3 – 25/12 = 5/4 = 1 1/4 (кв. ед).
Ответ: S = 1 1/4 кв. ед.
Мы разобрали примеры нахождения площадей фигур, ограниченных заданными линиями
. Для успешного решения подобных задач нужно уметь строить на плоскости линии и графики функций, находить точки пересечения линий, применять формулу для нахождения площади, что подразумевает наличие умений и навыков вычисления определенных интегралов.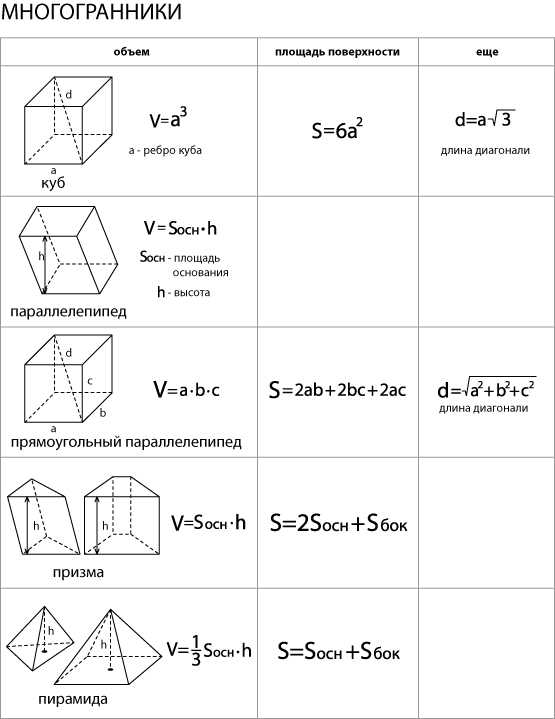
сайт,
при полном или частичном копировании материала ссылка на первоисточник обязательна.
Если вы планируете сделать ремонт самостоятельно, то у вас возникнет необходимость составить смету по строительным и отделочным материалам. Для этого вам понадобится рассчитать площадь помещения, в котором вы планируете произвести ремонтные работы. Главным помощником в этом выступает специально разработанная формула. Площадь помещения, а именно ее расчет, позволит вам сэкономить немалые деньги на строительных материалах и направить высвободившиеся денежные ресурсы в более нужное русло.
Геометрическая форма комнаты
Формула расчета площади помещения напрямую зависит от ее формы. Наиболее типичными для отечественных сооружений являются прямоугольные и квадратные комнаты. Однако в ходе перепланировки стандартная форма может искажаться. Комнаты бывают:
- Прямоугольные.
- Квадратные.
- Сложной конфигурации (например, круглые).
- С нишами и выступами.
Каждая из них имеет свои особенности расчета, но, как правило, используется одна и та же формула. Площадь помещения любой формы и размера, так или иначе, поддается вычислению.
Помещение прямоугольной или квадратной формы
Чтобы рассчитать площадь комнаты прямоугольной или квадратной формы, достаточно вспомнить школьные уроки геометрии. Поэтому для вас не должно составить особого труда определить площадь помещения. Формула расчета имеет вид:
S комнаты=A*B, где
А — длина помещения.
В — ширина помещения.
Для измерения этих величин вам понадобится обычная рулетка. Чтобы получить наиболее точные расчёты, стоит измерить стену с обеих сторон. Если значения не сходятся, возьмите за основу среднее значение получившихся данных. Но помните, что любые расчёты имеют свои погрешности, поэтому материал стоит закупать с запасом.
Помещение со сложной конфигурацией
Если ваша комната не попадает под определение «типичной», т.е.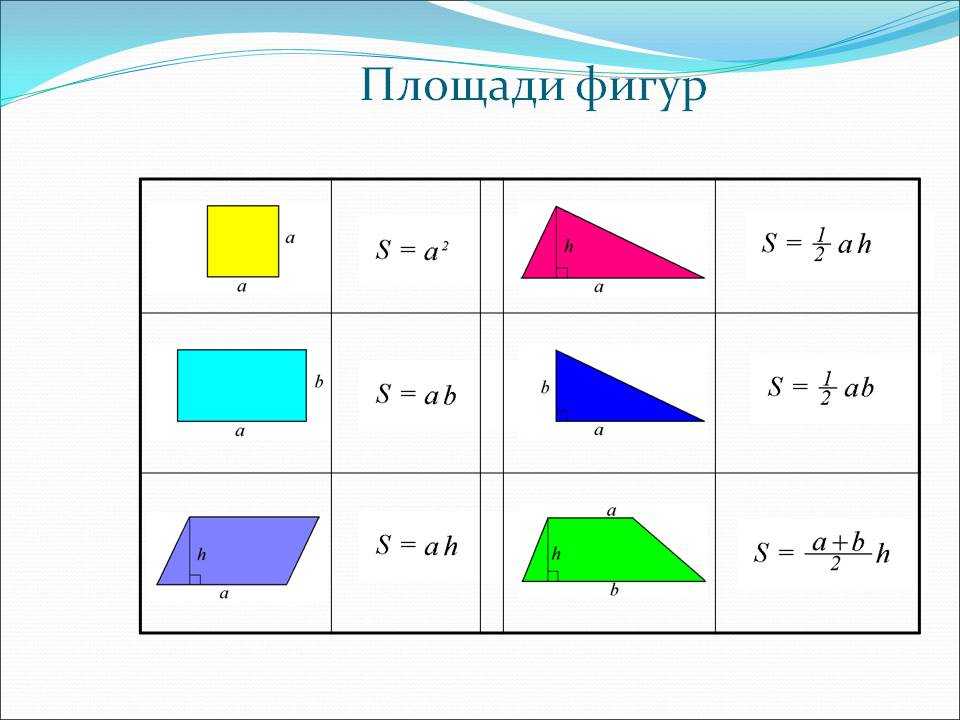
- Формула нахождения площади круга:
S комн.=π*R 2 , где
R — радиус помещения.
- Формула нахождения площади треугольника:
S комн.= √ (P(P — A) х (Р — В) х (Р — С)), где
Р — полупериметр треугольника.
А, В, С — длины его сторон.
Отсюда Р=А+В+С/2
Если в процессе расчета у вас возникли затруднения, то лучше не мучать себя и обратиться к профессионалам.
Площадь помещения с выступами и нишами
Зачастую стены украшают декоративными элементами в форме всевозможных ниш или выступов. Также их наличие может быть обусловлено необходимостью скрыть некоторые неэстетичные элементы вашей комнаты.
Площадь стены находится по формуле:
S стен = Р х С, где
Р — периметр
С — высота
Также нужно учитывать наличие окон и дверей. Их площадь необходимо отнять от получившегося значения.
Комната с многоуровневым потолком
Многоуровневый потолок не так сильно усложняет расчеты, как это кажется на первый взгляд. Если он имеет простую конструкцию, то можно произвести расчеты по принципу нахождения площади стен, осложненных нишами и выступами.
Однако если конструкция вашего потолка имеет дуго- и волнообразные элементы, то целесообразнее определить его площадь с помощью площади пола. Для этого необходимо:
- Найти размеры всех прямых участков стен.
- Найти площадь пола.
- Перемножить длину и высоту вертикальных участков.
- Суммировать получившееся значение с площадью пола.
Пошаговая инструкция по определению общей
площади помещения
- Освободите помещение от ненужных вещей. В процессе замеров вам понадобится свободный доступ ко всем участкам вашей комнаты, поэтому нужно избавиться от всего, что может этому препятствовать.
- Визуально разделите комнату на участки правильной и неправильной формы. Если ваше помещение имеет строго квадратную или прямоугольную форму, то этот этап можно пропустить.
- Сделайте произвольную схему помещения. Этот чертеж нужен для того, чтобы все данные были у вас всегда под рукой. Также он не даст вам возможности запутаться в многочисленных замерах.
- Замеры необходимо производить несколько раз. Это важное правило для исключения ошибок в подсчетах. Также если вы используете убедитесь, что луч лежит ровно на поверхности стены.
- Найдите общую площадь помещения. Формула общей площади помещения заключается в нахождении суммы всех площадей отдельных участков комнаты. Т.е. S общ.
= S стен+S пола+S потолка
Чтобы решить задачи по геометрии, надо знать формулы — такие, как площадь треугольника или площадь параллелограмма — а также простые приёмы, о которых мы расскажем.
Для начала выучим формулы площадей фигур. Мы специально собрали их в удобную таблицу. Распечатайте, выучите и применяйте!
Конечно, не все формулы по геометрии есть в нашей таблице. Например, для решения задач по геометрии и стереометрии во второй части профильного ЕГЭ по математике применяются и другие формулы площади треугольника. О них мы обязательно расскажем.
А что делать, если надо найти не площадь трапеции или треугольника, а площадь какой-либо сложной фигуры? Есть универсальные способы! Покажем их на примерах из банка заданий ФИПИ.
1. Как найти площадь нестандартной фигуры? Например, произвольного четырёхугольника? Простой приём — разобьём эту фигуру на такие, о которых мы всё знаем, и найдем её площадь — как сумму площадей этих фигур.
Разделим этот четырёхугольник горизонтальной линией на два треугольника с общим основанием, равным .
Ответ: .
2. В некоторых случаях площадь фигуры можно представить как разность каких-либо площадей.
Не так-то просто посчитать, чему равны основание и высота в этом треугольнике! Зато мы можем сказать, что его площадь равна разности площадей квадрата со стороной и трёх прямоугольных треугольников. Видите их на рисунке? Получаем: .
Ответ: .
3. Иногда в задании надо найти площадь не всей фигуры, а её части. Обычно речь здесь идет о площади сектора — части круга.Найдите площадь сектора круга радиуса , длина дуги которого равна .
На этом рисунке мы видим часть круга. Площадь всего круга равна , так как . Остается узнать, какая часть круга изображена. Поскольку длина всей окружности равна (так как ), а длина дуги данного сектора равна , следовательно, длина дуги в раз меньше, чем длина всей окружности. Угол, на который опирается эта дуга, также в раз меньше, чем полный круг (то есть градусов).
Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Сбор и использование персональной информации
Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.
От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.
Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.
Какую персональную информацию мы собираем:
- Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.
д.
Как мы используем вашу персональную информацию:
- Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
- Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
- Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
- Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.
Раскрытие информации третьим лицам
Мы не раскрываем полученную от Вас информацию третьим лицам.
Исключения:
- В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию.
Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
- В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.
Защита персональной информации
Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.
Соблюдение вашей конфиденциальности на уровне компании
Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.
Калькулятор площади планиметрических фигур — AndroidInsider.

Вычисляющий площади планиметрических фигур калькулятор Площадь фигур от разработчика Vitaly Karavan, которое можно загрузить из Google Play, является одним из тех приложений, которые с началом учебного года окажутся необходимыми многим учащимся. Ведь геометрия не только необходимый каждому учебный предмет, но и достаточно увлекательная наука, если творчески подойти к ее изучению, используя те возможности, которые предоставляют современные Android-девайсы и разработанное для них ПО.
Среди тех приложений, которые понадобятся студентам и школьникам в новом учебном году особое место занимают небольшие программные инструменты, позволяющие решать пусть одну, но очень часто возникающую в процессе учебы, задачу.
Как и следует из названия рассматриваемого калькулятора, он позволяет вычислять площадь геометрических фигур по заданным пользователем параметрам. Это, несомненно, поможет учащимся в решении многочисленных задач по геометрии.
К примеру, для того, чтобы вычислить площадь параллелограмма, необходимо ввести длину его стороны и высоту проведенного из верхнего угла перпендикуляра.
Интерфейс этого калькулятора весьма прост. Слева располагаются геометрические фигуры, на которых схематически показан тот способ вычисления их площади, который будет применяться, если пользователь коснется данной картинки.
С помощью рассматриваемого приложение можно вычислить площадь не только треугольника и круга, но также и сектора, сегмента, эллипса и кольца.
После ввода значений, необходимых для вычисления площади выбранной пользователем геометрической фигуры, нужно коснуться кнопки «Посчитать» и результат вычислений будет отображен в нижней части экрана приложения.
Среди преимуществ данного приложения следует особо отметить его легкость, как в отношении занимаемого пространства накопителя мобильного устройства, так и в смысле простоты его освоения даже теми людьми, которые не могут назвать себя уверенными и опытными пользователями мобильных девайсов. Воспользоваться приложением можно на смартфонах и планшетах под управлением Android 2.
Все это возможно в том числе и по той причине, что приложение является строго функциональным и его интерфейс лишен каких-либо дизайнерских излишеств, которые могли бы увеличить его объем и затруднить понимание программного инструмента множеством пользователей. При этом все необходимое для осуществления вычислений для которых оно предназначено в приложении присутствует.
Рассмотренный калькулятор — одно из множества размещенных в Google Play приложений, облегчающих учебу. Для решения треугольников можно воспользоваться калькулятором треугольников, способным производить те вычисления, которые необходимы именно в отношении данных геометрических фигур.
Существует даже калькулятор, в котором собраны все основы школьной геометрии. Ну а для тех, кому только предстоит пойти в школу полезной может оказаться игра, в процессе которой геометрические фигуры можно изучать в виртуальных зоопарке и лесу.
Приложения для решения каких задач необходимо еще до начала учебного года установить на свой девайс каждому студенту и школьнику?
- Приложение: Площадь фигур
- Разработчик: Vitaly Karavan
- Категория: Образование
- Версия: 1.
9
- Цена: Бесплатно
- Скачать: Google Play
- Приложением уже заинтересовались: 282 человека
- Теги
-
- Google Play
- Образование
- Операционная система Android
- Приложения для Андроид
Лонгриды для вас
Лучшие бесплатные игры для Android с открытым миром
Многие игры отличатся жанрами по принцип того, что надо делать. Шутеры, чтобы пострелять, квесты, чтобы подумать, гонки, чтобы гонять и так далее. Но есть игры, которые выносятся в отдельный жанр игр с открытым миром, хотя они предлагаю несколько жанров внутри себя. Просто в них можно делать все так, как вы захотите, а это уже стоит вынесения в отдельный жанр. Мы собрали для вас несколько отличных бесплатных игр с открытым миром, которых вам хватит не на одну неделю, если вы решите попробовать все из них.
Читать далее
Лучшие головоломки для Android: судоку
В нашей традиционной подборке игр мы уже много раз поднимали вопрос головоломок.
Читать далее
Зачем в смартфоне нужны предустановленные приложения и почему их так много
На новых смартфонах частенько неожиданно попадается большое количество приложений, которого явно не ожидаешь там увидеть: соцсети, браузеры, магазины приложений от производителя и много другого. Эти приложения уже загружены — в идеале, вам остается авторизоваться и начать ими пользоваться. Но на деле происходит так, что 70-80% программ удаляется со смартфона! А ведь, между прочим, за все эти предустановленные приложения разработчики заплатили немало денег производителям смартфоном.
Читать далее
Новый комментарий
Новости партнеров
-
Классные фишки Siri в iOS 16, которые стоит попробовать
-
Как правильно настроить Айфон и выспаться. Мой любимый способ
-
Как сделать Always On Display с черным экраном на iPhone 14 Pro как на Андроиде
-
Классные фишки Siri в iOS 16, которые стоит попробовать
Геометрические фигуры — Области
квадрат
Площадь квадрата может быть рассчитана как
A = A 2 (1a)
Сточа квадрата может быть рассчитана как
. A = A 1/2 (1B)
Диагональный квадрат можно рассчитать как
D = A 2 1/2 (1C)
прямоугольник
Площадь прямоугольника может быть рассчитана как
A = A B (2A)
Диагональ прямоугольника может быть рассчитана как
D = (A 2 + B 2 ) 1/2 (2B)
Параллелограмм
Площадь параллелограммы может быть рассчитана как
A = A H
= A B SNIC α (3A) 9000
= A B SNIC α (3A) 9000
= A B SNIC α (3A) 9000
= A B SNIC α (3A)
= A B SNIN параллелограмм можно рассчитать как
D 1 = ((A + H COT α ) 2 + H 2 ) 1/2 (3B)
D 2 = (A — — — — H COT α ) 2 + H 2 ) 1/2 (3B)
ЭКОЛИЗАТЕЛЬНЫЙ ТРЕЗОН
ЭКОЛИЗАТЕЛЬНЫЙ КРЕЙНГЛ — это треугольник, в котором равны все три стороны.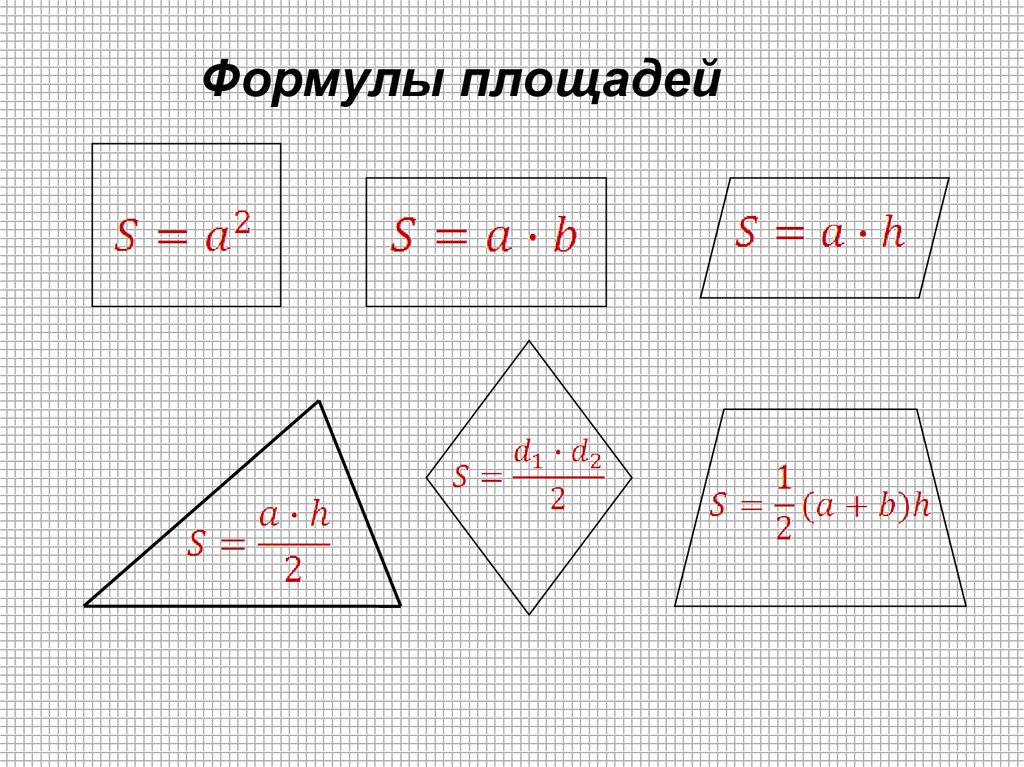
Площадь равностороннего треугольника можно вычислить как
A = A 2 /3 3 1/2 (4A)
Площадь равностороннего треугольника может быть рассчитана как
H = A/2 3 1/2 (4B)
Треугольник
Площадь треугольника может быть рассчитана как
A = A H / 2
= R S (5A)
R = A H / 2S (5B)
R = A H / 2S (5B)
R = A H / 2S (5B)
R = A H / 2S (5B)
.0014
R = B C / 2 H (5C)
S = (A + B + C) / 2 (5d)
X = S — A (5E)
Y = S = S — A (5E)
Y = S = S = S = S = S = S = S = S = S = S — A (5E)
Y = S = S = S = S = S = S = с. — B (5F)
Z = S — C (5G)
Трапезиоид
Площадь трапеции может быть рассчитана как
A = 1/2 (A + B) H
= M H (6A)
M = (A + B) / 2 (6B)
Hexagon
Область гексагона может быть рассчитана как
A = 3/2 A 2 3 1/2 (7A)
D = 2 A
= 2/3 1/2 S
= 1,1547005 S (7B)
= 1,1547005 S (7B)
= 1,1547005 S (7B)
= 1,1547005 S (7B)
= 1,1547005 S (7B)
= 1,1547005 S (7B)
= 1,1547005 S (7B) 0005
S = 3 1/2 /2 D
= 0,866025 D (7C)
Круг
Область круга может быть рассчитана как
.
= π r 2
= 0.785.. d 2 (8a)
C = 2 π r
= π D (8b)
, где
C = округ
- , сколько кругов входит в прямое в прямом эфире?
- Сколько меньших кругов помещается в большом круге?
Сектор и сегмент круга
Сектор круга
Площадь сектора круга может быть выражена как
A = 1/2 θ r r 2 (9)
= 1/360 θ D π r 2
, где
θ R = Угол в Radians
D = Угол в Radians
θ D = Угол в Radians θ D = угла в Radians D = угла в Radians θ D .
Сегмент круга
Площадь сегмента круга может быть выражена как
A = 1/2 (θ R — SIN θ R ) R 2
= 10012 2
= 1/12).
Правый круговой цилиндр
Площадь боковой поверхности правого круга может быть выражена как
A = 2 π R H (11)
5
где
h = высота цилиндра (м, фут)
r = радиус основания (м, фут) выражается как
A = π R L
= π R (R 2 + H 2 ) 1/2 (12)
, где
H = высота из CONESE (M.
H = высота CONE of CONE of CONE (M.
H = высота CONE of CON. , фут)
r = радиус основания (м, фут)
l = наклонная длина (м, фут)
Сфера
Площадь боковой поверхности сферы может быть выражена как 9001 9 = 4 π r 2 (13)
какова площадь фигуры? Определение, формула, примеры, факты
Геометрические фигуры – это фигуры с набором точек, соединенных линиями, образующими замкнутую фигуру.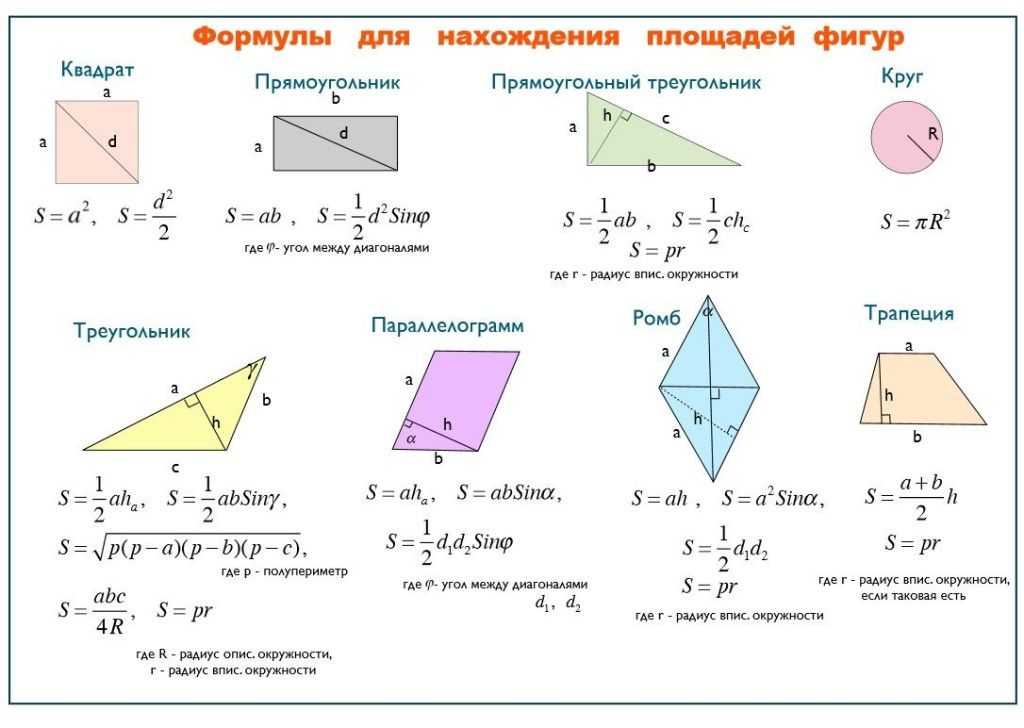
Например, , треугольник, квадрат, прямоугольник и четырехугольник — это фигуры с 3 и 4 точками, соединенными линиями. Фигуры с ограниченными кривыми не имеют сторон, но имеют окружность.
Площадь фигуры — это «пространство, ограниченное периметром или границей» данной формы. Мы вычисляем площадь для различных форм, используя математические формулы.
На следующих рисунках заштрихованная область обозначает область соответствующих фигур.
Единицей измерения площади всегда является квадрат единицы измерения длины. Результирующая единица является произведением единиц данных длин.
Формула площади применяется в архитектуре, геодезии и составлении карт. Масштабированная версия области для данного места полезна при разработке инструментов знаний, таких как глобусы и геофизические карты. Вычисление площади для двумерной формы — это первый шаг к интерпретации объема трехмерного объекта, такого как конус, цилиндр, шар и куб.
1
Какова площадь параллелограмма с основанием 4 см и высотой на 3 см больше основания?
12 кв.
14 кв. см
24 кв. см
28 кв. см
Правильный ответ: 28 кв. см
Высота параллелограмма = основание + 3 см,
т. е. 4 см + 3 см или 7 см.
Итак, площадь параллелограмма = основание ✕ высота = 7 см ✕ 4 см или 28 квадратных см.
2
Какова площадь прямоугольника шириной 5 единиц и длиной, удвоенной его ширины?
25 квадратных единиц
30 квадратных единиц
50 квадратных единиц
100 квадратных единиц
Правильный ответ: 50 квадратных единиц
Длина прямоугольника = 2 ✕ ширина,
т. е. 5 единиц или ✕ 1 единиц .
Итак, площадь прямоугольника = длина ✕ ширина = 10 единиц ✕ 5 единиц или 50 квадратных единиц.
3
Какова площадь фигуры, полученной путем соединения трех квадратов со стороной 3 см?
6 кв. см
9 кв. см
18 кв. см
27 кв. см
Правильный ответ: 27 кв. см квадратный см.
No related posts.



















































 = S стен+S пола+S потолка
= S стен+S пола+S потолка д.
д. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.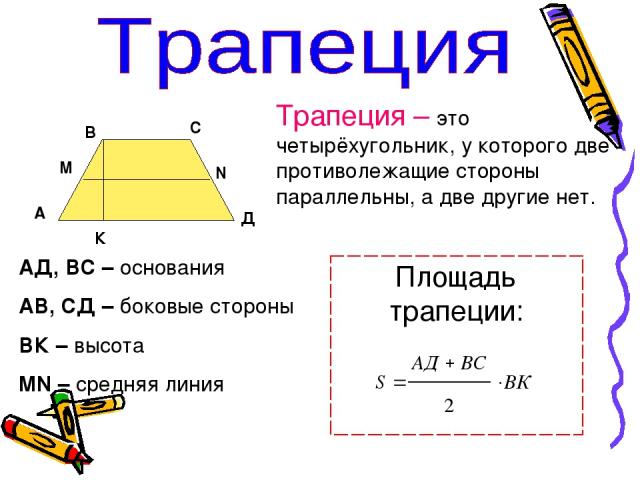 9
9