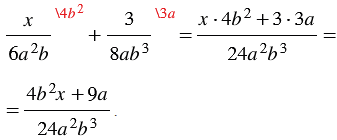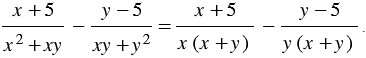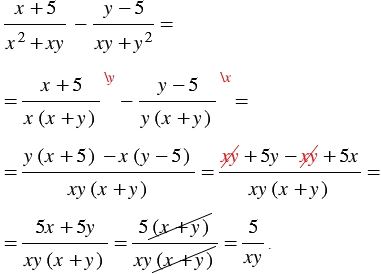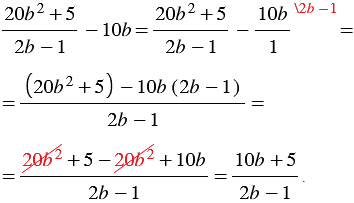Как найти общий множитель рациональных дробей - Avtoru.top

Приведение рациональных дробей к общему знаменателю

Общим знаменателем двух или нескольких рациональных Дробей называется целое рациональное выражение, которое делится на знаменатель каждой дроби.
Например, общим знаменателем дробей

является многочлен (x — 1)(2х + 1), однако не только он, но и многочлены 2(х-1)(2х + 1), 7х(х — 1)(2х + 1), 9х²(х-1)³(2х+1)² и Т. Д. Предпочтительнее взять наименьший общий знаменатель — такой простейший общий знаменатель, что любой другой общий знаменатель делится на этот простейший. Наименьшим общим
знаменателем дробей

является (х — 1)(2х + 1).
Можно записать:

Приведение исходных дробей к наименьшему общему знаменателю (в дальнейшем будем называть его просто общим знаменателем) было достигнуто умножением числителя и знаменателя первой дроби на (2х +1), а числителя и знаменателя второй дроби на (х-1). Многочлены (2х + 1) и (х-1) называют дополнительными множителями для первой и второй дробей соответственно. Таким образом, дополнительный множитель для данной дроби равен частному от деления общего знаменателя на знаменатель данной дроби.
Для того чтобы несколько рациональных дробей привести к общему знаменателю, необходимо:
1) разложить знаменатель каждой дроби на множители, если это возможно;
2) составить общий знаменатель, включив в него в качестве сомножителей все различные множители, полученные в пункте 1); если некоторый множитель имеется в нескольких разложениях, то он берется с показателем степени, равным наибольшему из имеющихся;
3) определить дополнительные множители для каждой из дробей, для чего общий знаменатель разделить на знаменатель каждой дроби;
4) умножить числитель и знаменатель каждой дроби на дополнительный множитель.
Пример. Привести дроби к общему знаменателю.

Решение.

Наименьшее общее кратное чисел 9, 36, 20 есть число 180. Отсюда общий знаменатель имеет вид 180·а³(а- 2b)(а + 2b). Дополнительные множители: 20а², 5(а + 2b), 9а(а — 2b),— для первой, второй и третьей дробей соответственно.
Окончательно получаем:

Источник

Приведение алгебраических дробей к общему знаменателю

Приведение алгебраических дробей к общему знаменателю выполняется по тем же правилам, что и приведение обыкновенных дробей к общему знаменателю. Следовательно, чтобы привести алгебраические дроби к общему знаменателю, нужно:

найти общий знаменатель для данных дробей;
найти дополнительный множитель для каждой дроби;
умножить числитель каждой дроби на её дополнительный множитель;
записать дроби с найденными новыми числителями и общим знаменателем.

Чтобы найти наименьший общий знаменатель для дробей, надо разложить знаменатель каждой дроби на множители и взять каждый множитель в наибольшей встречающейся степени.

Пример 1. Привести дроби к общему знаменателю:

2b	,	c	и	a	.
3a²	2b	6ab

Решение: Разложим знаменатели дробей на множители:

3a² = 3 · a²;

2b = 2 · b;

6ab = 2 · 3 · a · b.

Выпишем множители первого знаменателя и добавим к ним недостающие множители из второго и третьего знаменателя:

3 · a² · 2 · b = 6a²b.

Мы нашли наименьший общий знаменатель для данных дробей. Теперь, чтобы привести дроби к общему знаменателю, нам надо найти для каждой дроби дополнительный множитель. Для этого нужно разделить общий знаменатель на знаменатель каждой дроби:

6a²b : 3a² = 2b;

6a²b : 2b = 3a²;

6a²b : 6ab = a.

Умножаем числитель каждой дроби на её дополнительный множитель:

2b · 2b = 4b²;

c · 3a² = 3a²c;

a · a = a².

Осталось записать дроби с найденными новыми числителями и их общим знаменателем:

4b²	,	3a²c	и	a²	.
6a²b	6a²b	6a²b

Пример 2. Привести дроби к общему знаменателю:

Решение: Разложим на множители знаменатель второй дроби, используя формулу разности квадратов:

a² — 4 = a² — 2² = (a + 2)(a — 2).

Получившееся произведение и будет общим знаменателем для данных дробей. Значит, для приведения дробей к общему знаменателю, нам нужно только умножить числитель первой дроби на сумму чисел (a + 2).

3a · (a + 2) = 3a² + 6a.

В результате у нас получилось:

3a² + 6a	и	4	.
(a + 2)(a — 2)	(a + 2)(a — 2)

Произведение суммы и разности чисел a и 2 можно обратно свернуть в квадрат разности для более краткой записи дробей:

3a² + 6a	и	4	.
a² — 4	a² — 4

Источник

Главная
Справочники
Справочник по математике 5-9 класс
Рациональные выражения
Сложение и вычитание рациональных дробей с разными знаменателями

Чтобы сложить или вычесть рациональные дроби с разными знаменателями, нужно сначала привести эти дроби к общему знаменателю, после чего воспользоваться правилами сложения или вычитания рациональных дробей с одинаковыми знаменателями.

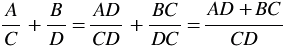
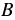
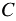
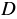
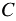
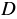
или , где , , и — многочлены, причём многочлены и — ненулевые.

Здесь в качестве общего знаменателя выбрано выражение, равное произведению знаменателей данных дробей. Но произведение знаменателей данных дробей не всегда является наиболее удобным общим знаменателем. Помним, что при нахождении общего знаменателя обыкновенных дробей мы находили наименьшее общее кратное знаменателей, раскладывая их на простые множители. Аналогично для нахождения общего знаменателя рациональных дробей может оказаться удобным предварительно разложить знаменатели на множители.

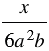
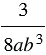
Пример 1. Найдите сумму дробей и .

Решение:

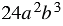
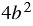
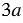
Знаменатели дробей представляют собой одночлены. Наиболее простым общим знаменателем является одночлен . Коэффициент этого одночлена равен наименьшему общему кратному коэффициентов знаменателей складываемых дробей, а каждая переменная взята с наибольшим показателем степени, с которым она входит в знаменатели дробей. Тогда дополнительным множителем к первой дроби будет одночлен , ко второй дроби — одночлен . Получаем:

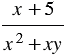
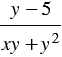
Пример 2. Найдите разность дробей и .

Решение:

Чтобы найти общий знаменатель вычитаемых дробей, разложим знаменатель каждой дроби на множители:

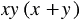
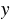
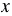
Простейшим общим знаменателем служит выражение . Тогда дополнительный множитель к первой дроби — , ко второй дроби — . Получаем:

Пример 3. Упростите выражение .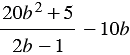

Решение:

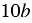
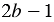
Представим выражение в виде дроби со знаменателем 1 и выполним вычитание дробей, учитывая то, что простейшим общим знаменателем дробей будет выражение . Получаем:

Обратите внимание, сумма и разность двух рациональных дробей являются рациональными дробями.

Советуем посмотреть:

Рациональные дроби

Основное свойство рациональной дроби

Сложение и вычитание рациональных дробей с одинаковыми знаменателями

Умножение и деление рациональных дробей. Возведение рациональной дроби в степень

Равносильные уравнения. Рациональные уравнения

Степень с целым отрицательным показателем

Свойства степени с целым показателем

Функция y=k/x и её график.

Рациональные выражения

Правило встречается в следующих упражнениях:

8 класс

Номер 104,
Мерзляк, Полонский, Якир, Учебник

Номер 116,
Мерзляк, Полонский, Якир, Учебник

Номер 122,
Мерзляк, Полонский, Якир, Учебник

Номер 127,
Мерзляк, Полонский, Якир, Учебник

Номер 130,
Мерзляк, Полонский, Якир, Учебник

Номер 8,
Мерзляк, Полонский, Якир, Учебник

Номер 184,
Мерзляк, Полонский, Якир, Учебник

Номер 192,
Мерзляк, Полонский, Якир, Учебник

Номер 9,
Мерзляк, Полонский, Якир, Учебник

Номер 290,
Мерзляк, Полонский, Якир, Учебник

Источник

Например, для дробей (frac{1}{5a}) и (frac{3}{b}) общим знаменателем будет (5ab), потому что именно это выражение содержит в себе все множители первого знаменателя (то есть, пятерку и (a)), а также все множители второго (это (b)).

Получается, что для нахождения общего знаменателя достаточно просто перемножить знаменатели всех дробей? Да, вообще говоря, это так. Однако на практике такой способ часто бывает неудобен, так как приводит к громоздким вычислениям в дальнейшем. Поэтому обычно находят наименьший общий знаменатель.

Например, для дробей (frac{1}{ab}) и (frac{3}{abc}) наименьшим общим знаменателем будет выражение (abc), но не (a^2 b^2c) (которое мы получим, если просто перемножим (ab) и (abc)).

Как искать наименьший общий знаменатель?

В приведенном выше примере наименьший общий знаменатель был очевиден. Однако в более сложных случаях его вот так сходу не напишешь.

Чтобы найти наименьший общий знаменатель нескольких дробей нужно все знаменатели разложить на множители, а потом собрать из этих множителей наименьший общий знаменатель.

Пример. Найдите общий знаменатель для дробей (frac{3}{x^2-5x}) и (frac{x}{x^2-25}).

Решение.

Пример. Найдите общий знаменатель для дробей (frac{a+1}{5a^2}), (frac{11-b}{a^3-9a}) и (frac{7}{(a-3)^2}).

Решение. И вновь раскладываем на множители знаменатели всех трех дробей, а потом собираем нашего «Франкенштейна»:

Общий знаменатель зависит только от знаменателей дробей, числители же на него не влияют вообще никак!

Поиск общего знаменателя важный этап при работе с алгебраическими дробями, а также при решении дробно-рациональных уравнений.

Скачать статью

Источник

Приведение рациональных дробей к общему знаменателю

Приведение алгебраических дробей к общему знаменателю

Советуем посмотреть:

Правило встречается в следующих упражнениях:

Как искать наименьший общий знаменатель?

Общий знаменатель зависит только от знаменателей дробей, числители же на него не влияют вообще никак!

Не пропустите также: