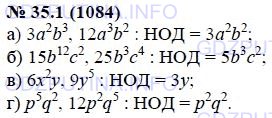Одночленом в алгебре называют произведение, состоящее из числового множителя и одной или нескольких переменных, возведённых в неотрицательные степени. Например, выражения
являются одночленами.
Говорят, что один одночлен делится на другой, если в результате деления получается одночлен. Например, одночлен делится на
но не делится на
так как
— в результате деления получается выражение, не являющееся одночленом.
Наибольший общий делитель двух одночленов
Одночлены и
делятся на одночлен
. Дейсвительно,
а
Поэтому
называют общим делителем одночленов
и
Определение. Общий делитель двух одночленов, содержащий каждую из переменных в наивысшей возможной степени, называется наибольшим общим делителем (НОД) этих одночленов.
Для того, чтобы найти НОД двух одночленов, нужно выбрать перменные, входящие в оба одночлена, затем выбрать наименьшие показатели степени, с которыми эти переменные входят в одночлены, и составить произведение переменных в этих степенях.
Наименьшее общее кратное двух одночленов
Одночлен делится на одночлены
и
:
Поэтому одночлен называется общим кратным одночленов
и
Определение. Наименьшим общим кратным (НОК) двух одночленов называется общее кратное этих одночленов, которое содержит каждую из переменных в наименьшей возможной степени.
Для того, чтобы найти НОК двух одночленов, нужно взять все перменные, входящие в эти одночлены, затем выбрать наибольшие показатели степени, с которыми эти переменные входят в одночлены, и составить произведение переменных в этих степенях.
Наименьшее общее кратное также определено с точностью до коэффициента.
← назад | далее →
Щебетун Виктор
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Одночлен
Определение 1
Выражения, являющиеся произведением чисел, переменных и их степеней, называются одночленами. Например, ${6х}^2,-11 sqrt{у, }{34a}^5b^4$. Также одночленами являются и сами числа, например $-243$, и переменные, например, y и их степени, например $x^{23}$.
Стандартным видом записи одночлен является такая, в которой на первом месте произведения стоит число, далее в произведении записаны переменные по их следовании в алфавите.
Например, одночлен ${34a}^5b^4$ записан в стандартном виде, а одночлен ${b^434a}^5$ — нет.
Число, стоящее на первом месте при стандартной записи одночлена, называется коэффициентом одночлена. Коэффициент одночлена ${34a}^5b^4$ равен $34$, а у одночлена $,-11 sqrt{y }$ равен $-11$.
Наибольший общий делитель
Наибольшее натуральное число, на которое делятся без остатка числа $a$ и $b$, называется наибольшим общим делителем и часто обозначается НОД.
Чтобы найти наибольший общий делитель двух чисел, необходимо:
1) разложить числа на простые множители
2) выбрать числа, которые входят в разложение этих чисел
3) найти произведение чисел, найденных на шаге $2$. Полученное число и будет искомым наибольшим общим делителем.
Пример 1
Найти НОД чисел $121$ и $132$.
Будем находить согласно представленному алгоритму. Для этого
-
разложить числа на простые множители
$242=2cdot 11cdot 11$
$132=2cdot 2cdot 3cdot 11$
-
Выбрать числа, которые входят в разложение этих чисел
$242=2cdot 11cdot 11$
$132=2cdot 2cdot 3cdot 11$
-
Найти произведение чисел, найденных на шаге $2$. Полученное число и будет искомым наибольшим общим делителем.
$НОД=2cdot 11=22$
Наибольший общий делитель одночленов
«Наибольший общий делитель (НОД) и наименьшее общее кратное (НОК) одночленов» 👇
Определение 2
Одночлен, на который делится каждый из исходных одночленов, называется общим одночленом.
Например, для одночленов $a^2b^3$ и abc общим одночленом будет одночлен $ab$.
Наибольшим общим делителем одночленов будет являться одночлен, содержащий общие переменные с наибольшими показателями степеней.
Например, для одночленов $a^4b^3$ и $a^2b^5c^3$ наибольшим общим делителем будет $a^2b^3$.
Чтобы найти наибольший общий делитель двух одночленов, необходимо:
1) найти переменные, входящие в состав каждого из исходных одночленов;
2) выбрать из показателей степеней выбранных переменных наименьшие и НОД коэффициентов исходных одночленов;
3) найти произведение переменных и чисел, найденных на шаге $2$. Полученный одночлен и будет искомым наибольшим общим делителем одночленов.
Пример 2
Найти НОД одночленов ${ 63a}^2b^6c^{11} $ и ${81a}^3b^4c^9$
Будем находить согласно представленному алгоритму. Для этого
-
найти переменные, входящие в состав исходных одночленов
${a}^2b^6c^{11} $ и $a^3b^4c^9$
-
выбрать из показателей степеней выбранных переменных наименьшие и НОД коэффициентов исходных одночленов
${a}^2b^6c^{11} $ и $a^3b^4c^9$
Найдем НОД коэффициентов одночленов, т.е. чисел $63$ и $81$
Разложим числа на простые множители
$63=3cdot 3cdot 7$
$81=3cdot 3cdot 3cdot 3$
Выбираем числа, которые входят в разложение этих чисел
$63=3cdot 3cdot 7$
$81=3cdot 3cdot 3cdot 3$
Найдем произведение чисел, найденных на шаге $2$. Полученное число и будет искомым наибольшим общим делителем.
$НОД=3cdot 3=9$
-
Найти произведение переменных и чисел, найденных на шаге $2$. Полученный одночлен и будет искомым наибольшим общим делителем одночленов
$НОД({63a}^2b^6c^{11} $ и ${81a}^3b^4c^9)=9a^2b^4c^9$
Наименьшее общее кратное двух чисел
Определение 3
Общими кратными чисел называются числа, которые делятся на исходные без остатка. Например, для чисел $25$ и $50$ общими кратными будут числа $50,100,150,200$ и т.д.
Наименьшее из общих кратных будет называться наименьшим общим кратным и обозначается НОК
Чтобы найти НОК двух чисел, необходимо:
-
Разложить числа на простые множители
-
Выписать множители, входящие в состав первого числа, и добавить к ним множители, которые входят в состав второго и не ходят в состав первого;
-
Найти произведение чисел, найденных на шаге $2$. Полученное число и будет искомым наименьшим общим кратным
Пример 3
Найти НОК чисел $9$ и $77$.
Будем находить согласно представленному алгоритму. Для этого
-
Разложить числа на простые множители:
$99=3cdot 3cdot 11$
$77=7cdot 11$
-
Выписать множители, входящие в состав первого:
$3,3,11 $
Добавить к ним множители, которые входят в состав второго и не ходят в состав первого:
$7$
-
Найти произведение чисел, найденных на шаге $2$. Полученное число и будет искомым наименьшим общим кратным
$НОК=3cdot 3cdot 11cdot 7=693$
Наименьшее общее кратное двух одночленов
Определение 4
Общим кратным двух одночленов называется одночлен, который делится на исходные без остатка. Например, для одночленов $b^6c^{11}$ и ${ b}^4c^9$ общими кратными будут одночлены $b^6c^{11}$, $b^7c^{22}$ и т.д. Наименьший из них и будет наименьшим общим кратным двух одночленов.
Чтобы найти НОК двух одночленов, необходимо:
1) Найти переменные, входящие в состав каждого из исходных одночленов;
2) Выбрать из показателей степеней выбранных переменных наибольшие степени и добавить к ним множители, которые входят в состав второго и не ходят в состав первого;
3) Найти произведение переменных, найденных на шаге $2$. Полученный одночлен и будет искомым наименьшим общим кратным одночленом.
Пример 4
Найти НОК${3a}^4b^7c^{12}d $ и ${8a}^3b^5c^9d^{12}$
Будем находить согласно представленному алгоритму. Для этого
-
Найти переменные, входящие в состав каждого из исходных одночленов
${a}^4b^7c^{12}d $ и $a^3b^5c^9d^{12}$
-
Выбрать из показателей степеней выбранных переменных наибольшие степени и добавить к ним множители, которые входят в состав второго и не ходят в состав первого
${a}^4b^7c^{12}d $ и $a^3b^5c^9d^{12}$
-
Найти произведение переменных, найденных на шаге $2$. Полученный одночлен и будет искомым наименьшим общим кратным одночленом
$НОК{3a}^4b^7c^{12}d $;${8a}^3b^5c^9d^{12}= {a}^4b^7c^{12}d^{12}$
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Найдите общий делитель для данных одночленов:
а)
3
a
2
b
3
,
12
a
3
b
2
;
б)
15
b
12
c
2
,
25
b
3
c
4
;
в)
6
x
2
y
,
9
y
5
;
г)
p
5
q
2
,
12
p
2
q
5
.
reshalka.com
ГДЗ учебник по алгебре 7 класс Мордкович. §35. Сокращение алгебраических дробей. Номер №35.1.
Решение а
Получай решения и ответы с помощью нашего бота
3
a
2
b
3
,
12
a
3
b
2
общий делитель:
3
a
2
b
2
Решение б
15
b
12
c
2
,
25
b
3
c
4
общий делитель:
5
b
3
c
2
Решение в
6
x
2
y
,
9
y
5
общий делитель:
3
y
Решение г
p
5
q
2
,
12
p
2
q
5
общий делитель:
p
2
q
2
Алгоритм отыскания общего множителя
нескольких одночленов
1.Найти наибольший общий делитель коэффициентов всех одночленов, входящих в многочлен, — он и будет общим числовым множителем (разумеется, это относится только к случаю целочисленных коэффициентов).
2.Найти переменные, которые входят в каждый член многочлена, и выбрать для каждой из них наименьший (из имеющихся) показатель степени.
3.Произведение коэффициента, найденного на первом шаге, и степеней, найденных на втором шаге, является общим множителем нескольких одночленов.
Алгоритм отыскания общего множителя
нескольких одночленов
1.Найти наибольший общий делитель коэффициентов всех одночленов, входящих в многочлен, — он и будет общим числовым множителем (разумеется, это относится только к случаю целочисленных коэффициентов).
2.Найти переменные, которые входят в каждый член многочлена, и выбрать для каждой из них наименьший (из имеющихся) показатель степени.
3.Произведение коэффициента, найденного на первом шаге, и степеней, найденных на втором шаге, является общим множителем нескольких одночленов.
Алгоритм отыскания общего множителя
нескольких одночленов
1.Найти наибольший общий делитель коэффициентов всех одночленов, входящих в многочлен, — он и будет общим числовым множителем (разумеется, это относится только к случаю целочисленных коэффициентов).
2.Найти переменные, которые входят в каждый член многочлена, и выбрать для каждой из них наименьший (из имеющихся) показатель степени.
3.Произведение коэффициента, найденного на первом шаге, и степеней, найденных на втором шаге, является общим множителем нескольких одночленов.
Алгоритм отыскания общего множителя
нескольких одночленов
1.Найти наибольший общий делитель коэффициентов всех одночленов, входящих в многочлен, — он и будет общим числовым множителем (разумеется, это относится только к случаю целочисленных коэффициентов).
2.Найти переменные, которые входят в каждый член многочлена, и выбрать для каждой из них наименьший (из имеющихся) показатель степени.
3.Произведение коэффициента, найденного на первом шаге, и степеней, найденных на втором шаге, является общим множителем нескольких одночленов.
Алгоритм отыскания общего множителя
нескольких одночленов
1.Найти наибольший общий делитель коэффициентов всех одночленов, входящих в многочлен, — он и будет общим числовым множителем (разумеется, это относится только к случаю целочисленных коэффициентов).
2.Найти переменные, которые входят в каждый член многочлена, и выбрать для каждой из них наименьший (из имеющихся) показатель степени.
3.Произведение коэффициента, найденного на первом шаге, и степеней, найденных на втором шаге, является общим множителем нескольких одночленов.
Классы
Все классы
- 7
- 8
- 9
Предметы
Все предметы
- Русский язык
- Английский язык
- Алгебра
- Геометрия
- Физика
войтирегистрация
- Ответкин
- Решебники
- 7 класс
- Алгебра
- Мордкович
- Задание №35.1
Назад к содержанию
ГДЗ (готовое домашние задание из решебника) на Задание №35.1 по учебнику Алгебра. 7 класс. Часть 2. Задачник для учащихся общеобразовательных учреждений / А.Г. Мордкович и др. — 17-е издание. Мнемозина, 2013-2019г.
Условие
Найдите общий делитель для данных одночленов:
а) 3а^2b^3, 12а^3b^2;
б) 15b^12с^2, 25b^3с^4;
в) 6х^2у, 9у^5;
г) р^5q^2, 12р^2q^5.
Решение 1
Другие задачи из этого учебника
Популярные решебники

Издатель: Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворова, 2013-2022г.

Издатель: А.Г. Мордкович и др., 2013-2019г.

Издатель: А.Г. Мерзляк, В.Б. Полонский, М.С. Якир. 2015-2022г.
Сообщить об ошибке
Выберите тип ошибки:
Решено неверно
Опечатка
Плохое качество картинки
Опишите подробнее
в каком месте ошибка
Ваше сообщение отправлено
и скоро будет рассмотрено
ОК, СПАСИБО