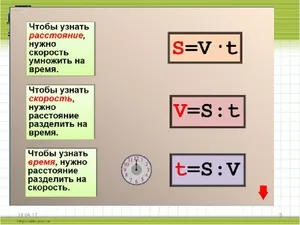
С древних времен людей беспокоит мысль о достижении сверх скоростей, так же как не дают покоя раздумья о высотах, летательных аппаратах. На самом деле это два очень сильно связанных между собой понятия. То, насколько быстро можно добраться из одного пункта в другой на летательном аппарате в наше время, зависит полностью от скорости. Рассмотрим же способы и формулы расчета этого показателя, а также времени и расстояния.
Как же рассчитать скорость?
На самом деле, рассчитать ее можно несколькими способами:
- через формулу нахождения мощности;
- через дифференциальные исчисления;
- по угловым параметрам и так далее.
В этой статье рассматривается самый простой способ с самой простой формулой — нахождение значения этого параметра через расстояние и время. Кстати, в формулах дифференциального расчета также присутствуют эти показатели. Формула выглядит следующим образом:
v=S/t, где
- v — скорость объекта,
- S — расстояние, которое пройдено или должно быть пройдено объектом,
- t — время, за которое пройдено или должно быть пройдено расстояние.
Как видите, в формуле первого класса средней школы нет ничего сложного. Подставив соответствующие значения вместо буквенных обозначений, можно рассчитать быстроту передвижения объекта. Например, найдем значение скорости передвижения автомобиля, если он проехал 100 км за 1 час 30 минут. Сначала требуется перевести 1 час 30 минут в часы, так как в большинстве случаев единицей измерения рассматриваемого параметра считается километр в час (км/ч). Итак, 1 час 30 минут равно 1,5 часа, потому что 30 минут есть половина или 1/2 или 0,5 часа. Сложив вместе 1 час и 0,5 часа получим 1,5 часа.
Теперь нужно подставить имеющиеся значения вместо буквенных символов:
v=100 км/1,5 ч=66,66 км/ч
Здесь v=66,66 км/ч, и это значение очень приблизительное (незнающим людям об этом лучше прочитать в специальной литературе), S=100 км, t=1,5 ч.
Таким нехитрым способом можно найти скорость через время и расстояние.
А что делать, если нужно найти среднее значение? В принципе, вычисления, показанные выше, и дают в итоге результат среднего значение искомого нами параметра. Однако можно вывести и более точное значение, если известно, что на некоторых участках по сравнению с другими скорость объекта была непостоянной. Тогда пользуются таким видом формулы:
vср=(v1+v2+v3+…+vn)/n, где v1, v2, v3, vn — значения скоростей объекта на отдельных участках пути S, n — количество этих участков, vср — средняя скорость объекта на всем протяжении всего пути.
Эту же формулу можно записать иначе, используя путь и время, за которое объект прошел этот путь:
- vср=(S1+S2+…+Sn)/t, где vср — средняя скорость объекта на всем протяжении пути,
- S1, S2, Sn — отдельные неравномерные участки всего пути,
- t — общее время, за которое объект прошел все участки.
Можно записать использовать и такой вид вычислений:
- vср=S/(t1+t2+…+tn), где S — общее пройденное расстояние,
- t1, t2, tn — время прохождения отдельных участков расстояния S.
Но можно записать эту же формулу и в более точном варианте:
vср=S1/t1+S2/t2+…+Sn/tn, где S1/t1, S2/t2, Sn/tn — формулы вычисления скорости на каждом отдельном участке всего пути S.
Таким образом, очень легко найти искомый параметр, используя данные выше формулы. Они очень просты, и как уже было указано, используются в начальных классах. Более сложные формулы базируются на этих же формулах и на тех же принципах построения и вычисления, но имеют другой, более сложный вид, больше переменных и разных коэффициентов. Это нужно для получения наиболее точного значения показателей.
Другие способы вычисления
Существую и другие способы и методы, которые помогают вычислить значения рассматриваемого параметра. В пример можно привести формулу вычисления мощности:
N=F*v*cos α , где N — механическая мощность,
F — сила,
v — скорость,
cos α — косинус угла между векторами силы и скорости.
Способы вычисления расстояния и времени
Можно и наоборот, зная скорость, найти значение расстояния или времени. Например:
S=v*t, где v — понятно что такое,
S — расстояние, которое требуется найти,
t — время, за которое объект прошел это расстояние.
Таким образом вычисляется значение расстояния.
Или вычисляем значение времени, за которое пройдено расстояние:
t=S/v, где v — все та же скорость,
S — расстояние, пройденный путь,
t — время, значение которого в данном случае нужно найти.
Для нахождения средних значений этих параметров существует довольно много представлений как данной формулы, так и всех остальных. Главное, знать основные правила перестановок и вычислений. А еще главнее знать сами формулы и лучше наизусть. Если же запомнить не получается, тогда лучше записывать. Это поможет, не сомневайтесь.
Пользуясь такими перестановками можно с легкостью найти время, расстояние и другие параметры, используя нужные, правильные способы их вычисления.
И это еще не предел!
Видео
В нашем видео вы найдете интересные примеры решения задач на нахождение скорости, времени и расстояния.
Общая характеристика
Скорость, время и расстояние являются физическими показателями, взаимосвязанными между собой процессом движения. На практике и теории известно равномерное и равноускоренное движение тел. Первый случай описывает постоянство времени, а второй — его изменение.
Основные понятия
Однозначное и конкретное определение тяжело сформулировать, но существуют разные концепции современной философской мысли в математике и физике. Течение времени является естественным процессом. Оно уходит, меняется все вокруг, совершаются разные события в мире, поэтому для физической меры характерен контекст событий.
Чтобы измерить время, нужно знать общие повторяющиеся события с одинаковым периодом. Это может быть смена дня, ночи или времени года. Чтобы определить единицу измерения времени (метр, час, секунда), ученые обращались к древнейшим источникам познаний.
Год состоит из двенадцати месяцев или четырех сезонов. Такое количество раз в весенний, летний, зимний и осенний периоды главный спутник Земли меняет свои фазы.
По мере развития прогресса измерение t модифицировалось, появлялись новые солнечные, водные, песчаные, огненные, механические, электронные и молекулярные измерители времени — часы.
Время включено в семь основных физических величин международной системы единиц СИ. Этот показатель используют для остальных составляющих. Четкое понимание t помогает проведению экспериментов и в обычной жизни.
Основной целью навигации и астрономии было измерение t. С 1000 по 1960 год секундное измерение воспринималось как 1/86400 дней. С 1970 г. это понятие видоизменилось, поскольку стала учитываться периодичность земной орбиты.
Самые точные мерила —швейцарские часы FOCS, измеряющие t с погрешностью хода в одну секунду за 30 млн лет.
Физическая величина отражает свойство материальных процессов, имеет определенную продолжительность, следует друг за другом. Взаимосвязан этот показатель с материей, движением, так как является формой его существования.
Длительность физического процесса, происходящего в определенной точке, устанавливают с помощью часов, расположенных в ней. Здесь используется прямое сравнение, уравнивается длительность процессов. Измерение продолжительности сводится к фиксированию начала и окончанию процесса на шкале. Когда говорят о фиксации показаний часов во время начала и завершения процесса, это не относится к фактическому месту их нахождения.
Теория относительности Эйнштейна меняет понимание времени, утверждая, что прогресс его не универсален и зависит от того, кто его изменяет. В такой картине реальности часы тикают с разной скоростью в зависимости от того, кто их носит.
Принимая большое ускорение или располагаясь рядом с сильными силами гравитации (вблизи черной дыры), можно изменить скорость течения времени, остановить его или возвратить. Для человека, находящегося внутри черной дыры, пространство и время кажутся взаимозаменяемыми, поэтому спуск в нее неизбежен, как и течение t вне этой области. Относительность уравнивает время и пространство.
Древняя система исчисления
До существования нашей эры люди привязывали отсчет времени к движению небесных тел или событий, связанных с ними. Древние народы искали основу для построения своей системы исчисления. В Вавилоне это было число 60, благодаря ему окружность содержит 360°, градус равен 60 минутам, а каждая из них состоит из 60 секунд.
Год представлялся окружностью в 360 градусов. Когда-то минимальной мерой исчисления был час. Жители Древнего Вавилона оказались сильны в математике, поэтому производили важные расчеты и решали задачи. Вводилась наименьшая единица времени. 60 минут составляют час, а в минуте столько же секунд.
Объяснение того, что сутки составляют 24 часа, а день делится пополам и равен 12 часам, выявили египтяне. Самой большой единицей измерения является индуистское и буддистское понятие Кальпа. Величина равна 4,32 млрд лет, что совпадает с возрастом планеты. Если перевести век Брахмы в обычные годы, получится 311 трлн и 40 млрд лет.
Первыми старинными часами являются солнечные мерила. Действие их основывается на изменении длины теней предметов по мере движения Солнца по небу. Такие часы внешне представляли собой длинный шест, воткнутый в землю. Затем возникли водяные, песчаные и огненные часы. Работа таких механизмов не привязывалась к движению Солнца, Луны либо звезд.
Первые механические мерила начали производиться мастерами Китая в 725 г. Жители Европы в Средние века устанавливали на башнях соборов часы, которые имели только одну часовую стрелку. Карманные измерители возникли в середине XVII века, а наручные намного позже.
В соответствии с международной системой измерения определение одной секунды привязано к периоду электромагнитного излучения, начинающемуся при переходе между тонкими уровнями основного состояния атома цезия-133. Одна секунда составляет 919 263 770 периодов.
Показатели физики
Не существует определенной концепции или класса времени. Показатель непрерывности процессов можно вычислить по формуле, проанализировать на графике или диаграмме.
Определения и концепции расчета
Термодинамика гласит, что время не вернуть. Его ход зависит от движения системы отсчета и может быть мгновенным.
Существует понятие «релятивистское замедление времени»: если часы находятся в неподвижной системе, то в движущемся теле все процессы замедлены. Этап старения для двух братьев-близнецов может пройти по-разному, если одного отправить в космос, а другого оставить на Земле. Человек в космосе не постареет, поскольку там изменяется масса его тела, а также замедляется гравитационное время. В условиях притяжения меняется ход часов. Чем сильнее поле гравитации, тем больше замедление. Между объектами, имеющими массу, создается взаимодействие.
Периодическая цепь событий рассчитывается неодинаково в зависимости от показателей. Зависимые величины:
- время;
- скорость;
- расстояние.
Секунда — стандартная единица, характеризующая время. Его определение в физике представляется как продолжительный показатель. Время через расстояние и скорость вычисляется по формуле t=S/V. Стандартная расшифровка:
- S — расстояние;
- V — конечная скорость (километровое значение);
- t — время.
Когда скорость измеряется в км/ч, то и время выражается в часах. В любой системе события развиваются одновременно.
Формула времени при равноускоренном движении выглядит как t = (V — V0)/a или t = S/(V — V0), где V0 — начальная скорость, a — ускорение. Таблица показателей:
| Вид движения | Скорость (V) | Перемещение (S) | Время (t) |
| Равномерное | V = знак постоянства (const) | S = Vt | t = S/V |
| Равноускоренное | V = V0+at | S = V0t+at2/2 | t = V-V0/a |
Атом изотопа цезия за секунду совершает 9192631770 собственных квантовых переходов. В зависимости от его расположения секунда имеет разные значения.
Решение задач
Понять действие формул времени при равномерном движении или равноускоренном можно, решив задачу. Многие сайты предлагают онлайн-калькулятор для удобного подсчета. В соответствующие графы достаточно ввести основные данные, после чего программа рассчитает все самостоятельно.
Задача 1. Автомобиль ехал со скоростью 200 км/ч и проехал всего 80 км. Требуется определить время движения машины. Условные обозначения:
- V — скорость;
- S — расстояние;
- t — время.
Показатели нужно перевести из километров в метры, из часов в секунды: 1 км = 1 тыс. м, 1 час = 3600 секунд. Получаем S = 80000 м, V= 200000/3600 = 55,55 м/с. Находим скорость по формуле: V= S/t = 80000/55,55 = 1440,14 сек.
t = 1440
14/3600 = 0,4 часа.
Ответ: автомобиль пройдет 0,4 ч.
При неравномерном движении путь, пройденный телом, равен произведению средней скорости на время, в течение которого тело перемещалось.
Задача 2. Движение точки задано уравнением: х = 2t — 0,03t2. Нужно определить, в какой период скорость точки сближения сравняется с нулевой отметкой. Коэффициенты равны 2м/с, 0,03 м/с2.
Условия задачи содержат функцию x (t). Скорость можно вычислить по формуле V = dx/dt = 2 — 0,06t Приравниваем скорость к 0, находим t:
2 — 0,06t = 0
t = 2/0,06 = 33,33 сек.
Необходимо определить зависимость модуля ускорения от времени: A (t)= dv/dt = -0,06.
Задача 3. Самолет для взлета набирает 350 км/ч. Нужно определить время разгона, если скорость достигается в конце взлетной полосы длиной в 2 км. Движение считается равноускоренным.
При равноускоренном движении формула выглядит как S = V0t+at2/2. При этом V= V0+at. Разгон самолета начинается с состояния покоя, то есть V0 = 0.
S = at2/2
V=at.
S = (V/t)*(t2/2) = Vt/2.
S = 2000 м
V=350 км/ч = 97,2 м/с.
t= 2S/V = 2*2000/97,2 = 41,15.
Благодаря вычислению известно, что разгон самолета длится 41,15 сек.
Задача 4. Скорость конькобежца составляет 15 м/с. Нужно вычислить время, за которое он пробежит путь 3 км.
V= 15 м/с.
S = 3 км (3000 м).
t = S/V = 3000/15 = 200
Ответ: за 200 секунд конькобежец пробежит 3 км.
Современная наука распределяет известные представления о времени в разные концепции — относительную и вещественную. По мнению относительной, в природе не существует временных рамок, а понятие времени является отношением между событиями. Время — проявление свойств физических тел и изменений, оно статично, как и пространство.
Когда лодка движется по течению, течение помогает лодке двигаться, и лодка начинает двигаться быстрее. Таким образом, скорость самой лодки и скорость течения объединяются.
Как рассчитать скорость формула
Скорость 90 км/ч означает, что объект проходит 90 км за один час.
Запишите тип скорости.
Формулы приводятся в математической нотации, а значения выражаются общими буквами (переменными).
V — скорость, V — расстояние, S — время, t — время.
Исходя из этого, уравнение скорости приобретает вид
Примените эту формулу для решения следующей задачи.
Автомобиль, движущийся с постоянной скоростью, проезжает 120 км за 2 часа. С какой скоростью двигался автомобиль?
Пройденное расстояние (дистанция) и время, затраченное на путь, были заменены формулой для нахождения скорости. V = 60 км/ч.
Теперь, исходя из формулы скорости, напишем формулу пути.
Поезд двигался со скоростью 50 км/ч в течение 3 часов равномерно. Какое расстояние было пройдено поездом за этот период?
Используя тип маршрута, мы нашли ответ. Поезд проехал 150 км за 3 часа.
Скорость — это физическая величина, определяющая расстояние, которое проходит объект за единицу времени. Поэтому уравнение для определения скорости (равномерного движения) может быть выражено как.
V, значение скорости — S, значение пройденного расстояния — T, время движения.
Скорость почти всегда выражается в м/с или км/ч, расстояние — в метрах (м) или километрах (км), а время — в секундах, минутах или часах.
Из перечисленных выше типов скоростей можно экспортировать определенные типы маршрутов.
Пройденное расстояние — это произведение скорости на время. Если известны расстояние и скорость, то время можно найти по следующей формуле
Разделите расстояние на скорость, чтобы найти время.
Вы можете использовать онлайн-калькуляторы для быстрого и точного расчета времени, скорости и расстояния в различных единицах измерения.
С древних времен людей волновала идея достижения сверхскорости, и никогда не волновала высота, летающих машин. На самом деле, это два очень тесно связанных понятия. То, насколько быстро вы сможете добраться из одной точки в другую на современном самолете, зависит исключительно от скорости. Рассматриваются методы и виды расчетов, а также время и расстояние.
Как же рассчитать скорость?
На самом деле, существует несколько методов расчета.
- через формулу нахождения мощности;
- через дифференциальные исчисления;
- по угловым параметрам и так далее.
В этой статье описан самый простой метод, в котором используется самое простое уравнение. Он заключается в нахождении значения этого параметра из расстояния и времени. Кстати, формула разности также содержит эти значения. Формула выглядит следующим образом.
- v — скорость объекта,
- S — расстояние, которое пройдено или должно быть пройдено объектом,
- t — время, за которое пройдено или должно быть пройдено расстояние.
Как видите, нет ничего сложного в том, чтобы быть первокурсником. Вы можете рассчитать скорость, с которой движется объект, подставив значения, соответствующие позициям букв. Например, давайте найдем значение скорости, с которой автомобиль проезжает 100 км за 1 час 30 минут. В большинстве случаев единицей измерения являются километры в час (км/ч), поэтому сначала нужно перевести 1 час 30 минут в часы. Это означает, что 1 час 30 минут равен 1,5 часа. Это потому, что 30 минут — это половина или 1/2 или 0,5 часа. Сумма 1 часа и 0,5 часа равна 1,5 часа.
Затем замените буквы алфавита на доступные значения.
Здесь v = 66,66 км/ч. Это значение очень приблизительное (неосведомленным лучше почитать о нем в специальной литературе), S = 100 км и t = 1,5ч.
С помощью этого простого метода скорость можно найти из времени и расстояния.
Что произойдет, если я захочу найти среднюю цену? Как правило, приведенный выше расчет приводит к среднему значению искомого параметра. Однако, если мы знаем, что скорость объекта не постоянна в определенном сечении по сравнению с другими сечениями, мы можем экспортировать более точные значения. В этом случае используйте тип.
V1, V2, V3 и VN — величины объектов на конкретном участке, n — количество этих участков, а VCR — средняя скорость на всех расстояниях.
Один и тот же тип можно записать по-разному, используя маршрут и время, которое объект прошел по этому маршруту.
- vср=(S1+S2+. +Sn)/t, где vср — средняя скорость объекта на всем протяжении пути,
- S1, S2, Sn — отдельные неравномерные участки всего пути,
- t — общее время, за которое объект прошел все участки.
Можно также написать его, используя вычисления такого типа.
- vср=S/(t1+t2+. +tn), где S — общее пройденное расстояние,
- t1, t2, tn — время прохождения отдельных участков расстояния S.
Однако тот же тип можно записать и в более точной форме
vcp = s1/t1+s2/t2+. +sn/tn, где s1/t1, s2/t2 и sn/tn — типы для расчета скорости на отдельных участках общего маршрута S.
Поэтому очень легко найти необходимые параметры, используя вышеуказанные типы. Он очень прост и, как уже говорилось, используется в начальном образовании. Самый сложный тип основан на том же типе и тех же принципах структуры и расчета, но имеет другой, более сложный формат, больше переменных и разные коэффициенты. Это необходимо для получения наиболее точной цены индикатора.
Другие способы вычисления
Существуют и другие методы и способы, помогающие рассчитать значение этого параметра. Примером может служить тип вычислительной мощности.
n = f*v*cos a, где n — механическая мощность, и
cos a — косинус угла между вектором силы и скоростью.
Скорость сближения — это расстояние, на которое два объекта приближаются друг к другу в единицах времени. Чтобы найти скорость сближения двух объектов, движущихся навстречу друг другу, необходимо суммировать скорости этих объектов.
Формула нахождения значений скорости, времени и расстояния
С древних времен людей волновала идея достижения сверхскорости, и никогда не волновала высота, летающих машин. На самом деле, это два очень тесно связанных понятия. То, насколько быстро вы сможете добраться из одной точки в другую на современном самолете, зависит исключительно от скорости. Рассматриваются методы и виды расчетов, а также время и расстояние.
На самом деле, существует несколько методов расчета.
- через формулу нахождения мощности;
- через дифференциальные исчисления;
- по угловым параметрам и так далее.
В данной статье рассматривается самый простой тип и самый простой метод — нахождение цены этого параметра через расстояние и время. Кстати, различные формулы включают эти значения. Мужчины следующие.
- v — скорость объекта,
- S — расстояние, которое пройдено или должно быть пройдено объектом,
- t — время, за которое пройдено или должно быть пройдено расстояние.
Как видите, ничего сложного для первоклассников нет. Вы можете вычислить скорость, с которой движется объект, подставив вместо буквы соответствующее значение. Например, найдите значение скорости, с которой автомобиль проезжает 100 километров за 1 час 30 минут. В большинстве случаев единицей измерения является один километр в час (км/ч), который сначала необходимо перевести в один час и 30 минут. Поэтому один час и 30 минут равны 1,5 часа, так как 30 минут — это половина, или половина, или 0,5 часа. При сложении 1 часа и 0,5 часа получается 1,5 часа.
Затем замените буквы алфавита на доступные значения.
Здесь v = 66,66 км/ч. Это значение очень приблизительное (неосведомленным лучше почитать о нем в специальной литературе), S = 100 км и t = 1,5ч.
С помощью этого простого метода скорость можно найти из времени и расстояния.
Что произойдет, если я захочу найти среднюю цену? Как правило, приведенный выше расчет приводит к среднему значению искомого параметра. Однако, если мы знаем, что скорость объекта не постоянна в определенном сечении по сравнению с другими сечениями, мы можем экспортировать более точные значения. В этом случае используйте тип.
V1, V2, V3 и VN — это значения для объектов на конкретном участке, n — количество этих участков, а VCR — средняя скорость на всех расстояниях.
Один и тот же тип можно записать по-разному, используя маршрут и время, которое объект прошел по этому маршруту.
- vср=(S1+S2+. +Sn)/t, где vср — средняя скорость объекта на всем протяжении пути,
- S1, S2, Sn — отдельные неравномерные участки всего пути,
- t — общее время, за которое объект прошел все участки.
Можно также написать его, используя вычисления такого типа.
- vср=S/(t1+t2+. +tn), где S — общее пройденное расстояние,
- t1, t2, tn — время прохождения отдельных участков расстояния S.
Однако тот же тип можно записать и в более точной форме
vcp = s1/t1+s2/t2+. +sn/tn, где s1/t1, s2/t2 и sn/tn — типы для расчета скорости на отдельных участках общего маршрута S.
Поэтому очень легко найти необходимые параметры, используя вышеуказанные типы. Он очень прост и, как уже говорилось, используется в начальном образовании. Самый сложный тип основан на том же типе и тех же принципах структуры и расчета, но имеет другой, более сложный формат, больше переменных и разные коэффициенты. Это необходимо для получения наиболее точной цены индикатора.
Другие способы вычисления
Существуют и другие методы и способы, помогающие рассчитать значение этого параметра. Примером может служить тип вычислительной мощности.
n = f*v*cos a, где n — механическая мощность, и
cos a — косинус угла между вектором силы и скоростью.
Способы вычисления расстояния и времени
Также можно найти цены расстояния и времени, зная скорость. Например:.
s = v*t, где v дает понять, что это такое, и
s — расстояние, которое вы хотите найти, и
t — время, необходимое объекту для прохождения этого расстояния.
При этом рассчитывается цена расстояния.
В качестве альтернативы рассчитайте значение времени прохождения расстояния.
t = s/v, где v — та же скорость и
s — пройденное расстояние, и
В данном случае это время, за которое нужно найти цену.
Существует несколько выражений этого типа и все остальные для нахождения среднего значения этих параметров. Самое главное — знать основные правила перевода и расчета. Еще важнее знать сами типы, причем желательно извне. Если вы не помните их, лучше запишите их. Это поможет, не сомневайтесь.
С помощью таких переводов можно легко найти время, расстояние и другие параметры, используя правильный способ их вычисления.
Водитель едет из города А в город Б, и через три часа к нему приближается мотоциклист со скоростью 60 км/ч. Водитель и мотоциклист встретились в 350 км от А. Расстояние между А и В составляет 470 км. Найдите скорость мотоциклиста.
Время
Время — это самое ценное, что у нас есть. Однако, помимо философии, время играет важную роль в математике.
Время — это продолжительность определенной деятельности или события.
Время обозначается латинской буквой t.
Наиболее распространенными единицами измерения времени являются секунды, минуты и часы.
на некоторое время.
Чтобы найти время, разделите расстояние на скорость.
Этот человек полезен, когда вы хотите узнать, сколько времени требуется вашему телу, чтобы преодолеть расстояние.
Взаимосвязь скорости, времени, расстояния
Скорость, время и расстояние тесно связаны между собой. Трудно представить себе человека без другого.
Если известны скорость и время движения, можно найти расстояние. Время равно скорости: s = v x t.
Работа 1. Мы вышли из нашего дома и посетили соседний двор. Нам потребовалось 15 минут, чтобы добраться до следующего сада. Наш спортивный браслет показывал, что наша скорость составляет 50 метров в минуту. Какое расстояние мы прошли?
Если мы проходим 50 метров в минуту, сколько из этих 50 метров мы проходим за 10 минут? Умножьте 50 метров в минуту на 15 минут, чтобы определить расстояние от дома до магазина.
Ответ: 750 метров пешком.
Если время и расстояние известны, найдите скорость: v = s:t.
Вопрос 2. Два ученика решили посмотреть, кто быстрее пробежит двор детской площадки. Расстояние между двором и детской площадкой составляет 100 метров. Первый выполняется за 25 секунд, а второй — за 50 секунд. Кто быстрее?
Самым быстрым считается тот, который проходит наибольшую длину за 1 секунду. Считается, что это самая высокая скорость. В этом вопросе скорость студента — это расстояние, пройденное за одну секунду.
Чтобы найти скорость, разделите расстояние на время. Чтобы найти скорость первого ученика, разделите 100 метров на время движения первого ученика, т.е. 25 секунд.
Если расстояние задано в метрах, а время движения в секундах, то скорость измеряется в метрах в секунду (м/с). Если расстояние указано в километрах, а продолжительность времени в часах, то скорость измеряется в километрах в час (км/ч).
В нашей задаче расстояние задано в виде измерения, а время в секундах. Это позволяет измерять скорость в метрах в секунду (м/с).
Таким образом, мы узнаем, что скорость первого ученика составляет 4 метра в секунду.
Затем мы можем найти скорость второго ученика. Для этого разделите расстояние на время движения второго ученика, т.е. 50 секунд.
Таким образом, скорость второго ученика составляет 2 метра в секунду.
Теперь вы можете сравнить скорость каждого ученика и определить, кто бежал быстрее.
Скорость первого ученика выше. Так он быстрее добирался до корта.
ОТВЕТ: первый ученик бежал быстрее.
Если скорость и расстояние известны, можно найти время: t = s:v.
Вопрос 3: Стадион находится в 500 метрах от школы. Мы должны идти туда пешком. Скорость составляет 100 метров в минуту. Сколько времени нужно, чтобы дойти от школы до стадиона?
Если мы проходим 100 метров в минуту, сколько минут в 100 метрах нам нужно, чтобы пройти 500 метров?
Чтобы ответить на этот вопрос, нужно разделить 500 метров на 1 минуту, то есть на расстояние, которое вам нужно пройти до 100. Затем требуется время, чтобы достичь этой стадии.
Ответ: дойти от школы до суда за пять минут.
Печатайте или рисуйте таблицы, особенно в математических курсах, чтобы быстрее запомнить и применить скорость, время и расстояние.
Например, определите угловую скорость преобразователя, когда подвешенная масса перемещается на 10 метров. Радиус руки равен 40 см. В начале подвеса он находится в состоянии покоя и начинает спускаться с ускорением A = 0,04 м/S2.
Единицы измерения скорости
Основной единицей измерения скорости в системе СИ является: V = M/S2
Задание. Движение точки A задается уравнением: $ x = 2 t^-4 t^$. Пойнт начинает свое движение.0= 0 c. Как движется ось под осью в момент времени t = 0,5 с?
Решение. Найдите уравнение, определяющее скорость этой точки. Для этого получите первую производную по времени от функции x = x(t), заданной в условиях задачи.
Чтобы определить направление движения, заменим полученную функцию скорости на v = v(t) в (1.1) и сравним результат с нулем за время, определенное конвенцией.
Получив свою скорость в этой точке, материальная точка будет двигаться по оси x, так как ее скорость отрицательна.
Ответ. Ось x.
Мы уже помогли 4372 студентам старших классов и колледжей сдать экзамены, начиная с решения задач и заканчивая бакалаврской работой! Узнайте, сколько будет стоить ваша работа за 15 минут!
Задание. Скорость материала точки является функцией времени формы.
Скорость в м/с, время в с. Каковы координаты точки в момент времени t = 10 с? Считайте, что в момент t = 0 c точка начала двигаться вдоль оси x от своей начальной точки.
Разрешение. Точка движется вдоль оси x, и связь между координатами x и скоростью имеет следующий вид
Чтобы ответить на первый вопрос задачи, давайте поменяем в уравнении (2.1) время t = 10 c.
Чтобы определить точку, в которой достигается 10 м от начала, пусть уравнение (2.1) равно 10 и пусть следующее квадратное уравнение равно.
$ begin 10 t-t^= 10 (2.2) ǫ t_ = 5+ ǫ sqrt compx 8.8 (c); t_ = 5- sqrt amptx 1.13 (c) ǫ end $
Рассмотрим второй вариант нахождения точки на расстоянии 10 м от начала, когда x = -10. Решение квадратного уравнения:.
При решении уравнения (2.3) скорректируйте следующий маршрут
Ответ. 1) $ x = 0 mathrm $ 2) $ t_ = 8.8 mathrm, t_ = 1.13 c, t_ = 11 c $
«Формула времени. Решение задач»
Скорость, время и расстояние — физические величины, взаимосвязаны процессом движения. Виды движений: 1) равномерное (прямолинейное, криволинейное и по окружности), 2) равноускоренное (с постоянным ускорением), 3) гармоническое. Для каждого вида движения своя формула времени.
Время обозначается как t. Единица измерения времени – с (секунды).
Самая простая формула при равномерном прямолинейном движении. Время, необходимое для прохождения пути равняется частному от деления пути на скорость равномерного прямолинейного движения: t = S / v.
При равноускоренном движении время равняется частному от деления разницы конечной и начальной скорости на ускорение: t = (v — v0) / a или частному от деления пути на разность конечной и начальной скорости: t = S / (v — v0).
Решение задач через формулу времени
Задача № 1.
Конькобежец может развивать скорость до 13 м/с. За какое время он пробежит дистанцию длиной 2,6 км?

Задача № 2.
Двигаясь с ускорением 5 м/с2 скорость космической ракеты увеличилась на 100 м/с. За какое время произошло такое изменение скорости?
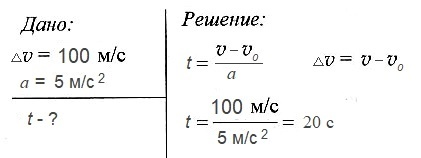
Задача № 3.
Пункты А и В находятся на берегу реки на некотором расстоянии друг от друга. Моторная лодка проходит расстояние АВ вниз по течению реки за время t1 = 3 ч, а плот то же расстояние – за время t0 =12 ч. Какое время t2 затратит моторная лодка на обратный путь?
Решение. Обозначим расстояние между пунктами А и В через L, скорость моторной лодки относительно воды через vл , а скорость течения через vт. Тогда t0 = L / vт , t1 = L / (vл + vт) , t2 = L / (vл — vт) . Исключая из записанной системы уравнений L, vл и vт
находим
Ответ: 6 ч.
Конспект урока «Формула времени. Решение задач».
Следующая тема: «».
Расчёт
пути и времени движения
«Движение
– это жизнь»
Аристотель
В
данной теме будем применять приобретённые знания о механическом движении на
практике. Прежде чем начать решать задачи, вспомним, необходимые определения. Путь
– это физическая величина, равная длине траектории, по которой двигалось тело,
в течение данного промежутка времени. Путь является скалярной величиной,
то есть, не имеет направления. Скорость при равномерном движении – это
величина, равная отношению пройденного пути к промежутку времени, за который
этот путь пройден.
Скорость
является векторной величиной, то есть, характеризуется как числовым значением,
так и направлением.
Средняя
скорость при неравномерном движении – это величина, равная отношению всего
пройденного пути к общему времени в пути.
Задача
1.
Какой путь пройдет автомобиль, двигаясь равномерно со скоростью 75 км/ч за 20 минут?
В
первую очередь, необходимо научиться правильно оформлять задачи по физике.
При решении любой задачи нужно писать «дано». То есть, в левой части
листа необходимо записать слово «дано», после которого ставится двоеточие, а
дальше в столбик перечисляете все исходные данные, которые указаны в условии
задачи. В нашем случае – это скорость и время в пути. После этого, нужно
очеркнуть данные и ниже (уже под линией) записать, что необходимо найти.
В задаче спрашивается, какой путь пройдет автомобиль. Дальше приступаем
непосредственно к решению задачи.
А
теперь обратите внимание вот на что: скорость в условии задачи дана в км/ч, то есть,
сколько километров автомобиль проходит за час. А время в условии дано в
минутах. Поэтому, прежде чем делать вычисления, необходимо перевести минут в
часы.
В
общем и целом, этот способ правильный. Но, чтобы не запутаться с единицами
измерения, можно (и даже нужно) переводить данные в систему СИ сразу после
того, как записано «дано». Напомним, что для перевода км/ч в м/с или м/с в
км/ч необходимо
1 м/с = 3,6 км/ч
1 км/ч = 1/3,6 м/с
Время
в системе СИ измеряется в секундах. В одной минуте шестьдесят секунд, поэтому,
чтобы перевести минуты в секунды, нужно минуты умножить на 60. После того, как
перевели все данные в систему СИ, необходимо очеркнуть и эту колонку, а правее
пишитсяе само решение. Решение и ответ будут одинаковыми. Однако рекомендуется
переводить данные в систему СИ.
Задача
2.
Мотоциклист проехал 5 км вдвое быстрее, чем следующие 7 км. Найдите его среднюю скорость, если общее время в пути составило 10 минут.
Получившееся
выражение, в котором остались, только те величины, которые были даны
изначально, называется расчетной формулой. Только в расчетную формулу необходимо
подставлять числовые значения, а до этого, все делается в буквенном виде.
Задача
3.
Самолет взлетел, после чего пролетел 120 км на определенной высоте, а потом приземлился. Известно, что пути, пройденные в процессе взлета и посадки равны 120 км каждый. Во время взлета и посадки, скорость самолета была равна 200 м/с, а во время остального
пути – 250 м/с. Какое время самолет затратил на весь путь? Какова средняя
скорость?
Сразу
хочется обратить ваше внимание на распространенную ошибку. Среднюю
скорость нельзя находить как среднее арифметическое разных скоростей на разных
участках движения. В этом можно убедиться с помощью простых расчетов:
если подсчитать среднюю скорость, как среднее арифметическое скоростей, то
получим 216,7 м/с. Этот результат неправильный. Теперь подсчитаем среднюю
скорость как отношение всего пройденного пути к общему времени в пути. В
результате получим 214,3 м/с. Получается вроде небольшая разница. В
результате неверных расчётов за каждую секунду, пройденное расстояние
увеличивается на 2,4 м/с. Поэтому, при неверном расчете за час пройденное
расстоянии будет больше на 8,6 км, а это существенно.
Задача
4.
Средняя скорость движения велосипедиста равна 8 м/с. Известно, что первую часть
своего пути велосипедист проехал за 3 минуты. За какое время велосипедист
проехал вторую часть, если общий путь составил 2 км?
Задача
5.
Определите по графику скорость равномерного движения тела.
Здесь,
конечно, никаких данных, кроме самого графика нет, поэтому, «дано» писать не
нужно. В таких заданиях, в первую очередь нужно посмотреть на оси графика:
какие величины они обозначают и в каких единицах измеряются. Вертикальная ось –
обозначает пройденный путь в метрах, а горизонтальная ось – время в минутах.
Значит, это график зависимости пройденного пути от времени. При равномерном
движении скорость постоянна, значит, можно путь, пройденный за определенный
промежуток времени, разделить на это время и, таким образом, найти скорость.
Для наибольшей точности желательно найти точку, на графике, наиболее близкую к
пересечению клеточек. Когда нашли такую точку, смотрим на соответствующие
координаты, то есть, на значения пути и времени. Для этого из точки опускаем
перпендикуляры на обе оси. Теперь, когда получили значение координат, можно определить скорость.
Основные
выводы:
В
качестве итогов урока, рассмотрим общий алгоритм решения задач на движение.