Общая характеристика
Скорость, время и расстояние являются физическими показателями, взаимосвязанными между собой процессом движения. На практике и теории известно равномерное и равноускоренное движение тел. Первый случай описывает постоянство времени, а второй — его изменение.
Основные понятия
Однозначное и конкретное определение тяжело сформулировать, но существуют разные концепции современной философской мысли в математике и физике. Течение времени является естественным процессом. Оно уходит, меняется все вокруг, совершаются разные события в мире, поэтому для физической меры характерен контекст событий.
Чтобы измерить время, нужно знать общие повторяющиеся события с одинаковым периодом. Это может быть смена дня, ночи или времени года. Чтобы определить единицу измерения времени (метр, час, секунда), ученые обращались к древнейшим источникам познаний.
Год состоит из двенадцати месяцев или четырех сезонов. Такое количество раз в весенний, летний, зимний и осенний периоды главный спутник Земли меняет свои фазы.
По мере развития прогресса измерение t модифицировалось, появлялись новые солнечные, водные, песчаные, огненные, механические, электронные и молекулярные измерители времени — часы.
Время включено в семь основных физических величин международной системы единиц СИ. Этот показатель используют для остальных составляющих. Четкое понимание t помогает проведению экспериментов и в обычной жизни.
Основной целью навигации и астрономии было измерение t. С 1000 по 1960 год секундное измерение воспринималось как 1/86400 дней. С 1970 г. это понятие видоизменилось, поскольку стала учитываться периодичность земной орбиты.
Самые точные мерила —швейцарские часы FOCS, измеряющие t с погрешностью хода в одну секунду за 30 млн лет.
Физическая величина отражает свойство материальных процессов, имеет определенную продолжительность, следует друг за другом. Взаимосвязан этот показатель с материей, движением, так как является формой его существования.
Длительность физического процесса, происходящего в определенной точке, устанавливают с помощью часов, расположенных в ней. Здесь используется прямое сравнение, уравнивается длительность процессов. Измерение продолжительности сводится к фиксированию начала и окончанию процесса на шкале. Когда говорят о фиксации показаний часов во время начала и завершения процесса, это не относится к фактическому месту их нахождения.
Теория относительности Эйнштейна меняет понимание времени, утверждая, что прогресс его не универсален и зависит от того, кто его изменяет. В такой картине реальности часы тикают с разной скоростью в зависимости от того, кто их носит.
Принимая большое ускорение или располагаясь рядом с сильными силами гравитации (вблизи черной дыры), можно изменить скорость течения времени, остановить его или возвратить. Для человека, находящегося внутри черной дыры, пространство и время кажутся взаимозаменяемыми, поэтому спуск в нее неизбежен, как и течение t вне этой области. Относительность уравнивает время и пространство.
Древняя система исчисления
До существования нашей эры люди привязывали отсчет времени к движению небесных тел или событий, связанных с ними. Древние народы искали основу для построения своей системы исчисления. В Вавилоне это было число 60, благодаря ему окружность содержит 360°, градус равен 60 минутам, а каждая из них состоит из 60 секунд.
Год представлялся окружностью в 360 градусов. Когда-то минимальной мерой исчисления был час. Жители Древнего Вавилона оказались сильны в математике, поэтому производили важные расчеты и решали задачи. Вводилась наименьшая единица времени. 60 минут составляют час, а в минуте столько же секунд.
Объяснение того, что сутки составляют 24 часа, а день делится пополам и равен 12 часам, выявили египтяне. Самой большой единицей измерения является индуистское и буддистское понятие Кальпа. Величина равна 4,32 млрд лет, что совпадает с возрастом планеты. Если перевести век Брахмы в обычные годы, получится 311 трлн и 40 млрд лет.
Первыми старинными часами являются солнечные мерила. Действие их основывается на изменении длины теней предметов по мере движения Солнца по небу. Такие часы внешне представляли собой длинный шест, воткнутый в землю. Затем возникли водяные, песчаные и огненные часы. Работа таких механизмов не привязывалась к движению Солнца, Луны либо звезд.
Первые механические мерила начали производиться мастерами Китая в 725 г. Жители Европы в Средние века устанавливали на башнях соборов часы, которые имели только одну часовую стрелку. Карманные измерители возникли в середине XVII века, а наручные намного позже.
В соответствии с международной системой измерения определение одной секунды привязано к периоду электромагнитного излучения, начинающемуся при переходе между тонкими уровнями основного состояния атома цезия-133. Одна секунда составляет 919 263 770 периодов.
Показатели физики
Не существует определенной концепции или класса времени. Показатель непрерывности процессов можно вычислить по формуле, проанализировать на графике или диаграмме.
Определения и концепции расчета
Термодинамика гласит, что время не вернуть. Его ход зависит от движения системы отсчета и может быть мгновенным.
Существует понятие «релятивистское замедление времени»: если часы находятся в неподвижной системе, то в движущемся теле все процессы замедлены. Этап старения для двух братьев-близнецов может пройти по-разному, если одного отправить в космос, а другого оставить на Земле. Человек в космосе не постареет, поскольку там изменяется масса его тела, а также замедляется гравитационное время. В условиях притяжения меняется ход часов. Чем сильнее поле гравитации, тем больше замедление. Между объектами, имеющими массу, создается взаимодействие.
Периодическая цепь событий рассчитывается неодинаково в зависимости от показателей. Зависимые величины:
- время;
- скорость;
- расстояние.
Секунда — стандартная единица, характеризующая время. Его определение в физике представляется как продолжительный показатель. Время через расстояние и скорость вычисляется по формуле t=S/V. Стандартная расшифровка:
- S — расстояние;
- V — конечная скорость (километровое значение);
- t — время.
Когда скорость измеряется в км/ч, то и время выражается в часах. В любой системе события развиваются одновременно.
Формула времени при равноускоренном движении выглядит как t = (V — V0)/a или t = S/(V — V0), где V0 — начальная скорость, a — ускорение. Таблица показателей:
| Вид движения | Скорость (V) | Перемещение (S) | Время (t) |
| Равномерное | V = знак постоянства (const) | S = Vt | t = S/V |
| Равноускоренное | V = V0+at | S = V0t+at2/2 | t = V-V0/a |
Атом изотопа цезия за секунду совершает 9192631770 собственных квантовых переходов. В зависимости от его расположения секунда имеет разные значения.
Решение задач
Понять действие формул времени при равномерном движении или равноускоренном можно, решив задачу. Многие сайты предлагают онлайн-калькулятор для удобного подсчета. В соответствующие графы достаточно ввести основные данные, после чего программа рассчитает все самостоятельно.
Задача 1. Автомобиль ехал со скоростью 200 км/ч и проехал всего 80 км. Требуется определить время движения машины. Условные обозначения:
- V — скорость;
- S — расстояние;
- t — время.
Показатели нужно перевести из километров в метры, из часов в секунды: 1 км = 1 тыс. м, 1 час = 3600 секунд. Получаем S = 80000 м, V= 200000/3600 = 55,55 м/с. Находим скорость по формуле: V= S/t = 80000/55,55 = 1440,14 сек.
t = 1440
14/3600 = 0,4 часа.
Ответ: автомобиль пройдет 0,4 ч.
При неравномерном движении путь, пройденный телом, равен произведению средней скорости на время, в течение которого тело перемещалось.
Задача 2. Движение точки задано уравнением: х = 2t — 0,03t2. Нужно определить, в какой период скорость точки сближения сравняется с нулевой отметкой. Коэффициенты равны 2м/с, 0,03 м/с2.
Условия задачи содержат функцию x (t). Скорость можно вычислить по формуле V = dx/dt = 2 — 0,06t Приравниваем скорость к 0, находим t:
2 — 0,06t = 0
t = 2/0,06 = 33,33 сек.
Необходимо определить зависимость модуля ускорения от времени: A (t)= dv/dt = -0,06.
Задача 3. Самолет для взлета набирает 350 км/ч. Нужно определить время разгона, если скорость достигается в конце взлетной полосы длиной в 2 км. Движение считается равноускоренным.
При равноускоренном движении формула выглядит как S = V0t+at2/2. При этом V= V0+at. Разгон самолета начинается с состояния покоя, то есть V0 = 0.
S = at2/2
V=at.
S = (V/t)*(t2/2) = Vt/2.
S = 2000 м
V=350 км/ч = 97,2 м/с.
t= 2S/V = 2*2000/97,2 = 41,15.
Благодаря вычислению известно, что разгон самолета длится 41,15 сек.
Задача 4. Скорость конькобежца составляет 15 м/с. Нужно вычислить время, за которое он пробежит путь 3 км.
V= 15 м/с.
S = 3 км (3000 м).
t = S/V = 3000/15 = 200
Ответ: за 200 секунд конькобежец пробежит 3 км.
Современная наука распределяет известные представления о времени в разные концепции — относительную и вещественную. По мнению относительной, в природе не существует временных рамок, а понятие времени является отношением между событиями. Время — проявление свойств физических тел и изменений, оно статично, как и пространство.
Содержание материала
- Как же рассчитать скорость?
- Видео
- Молекулярная физика
- Единицы измерения времени
- Скорость
- Формулы для расчета пути и времени движения при неравномерном движении тела
- Импульс
- Самая большая единица измерения времени
- Основные формулы электричества
- График пути равномерного движения
- Решение задач
Как же рассчитать скорость?
На самом деле, рассчитать ее можно несколькими способами:
- через формулу нахождения мощности;
- через дифференциальные исчисления;
- по угловым параметрам и так далее.
В этой статье рассматривается самый простой способ с самой простой формулой — нахождение значения этого параметра через расстояние и время. Кстати, в формулах дифференциального расчета также присутствуют эти показатели. Формула выглядит следующим образом:
v=S/t, где
- v — скорость объекта,
- S — расстояние, которое пройдено или должно быть пройдено объектом,
- t — время, за которое пройдено или должно быть пройдено расстояние.
Как видите, в формуле первого класса средней школы нет ничего сложного. Подставив соответствующие значения вместо буквенных обозначений, можно рассчитать быстроту передвижения объекта. Например, найдем значение скорости передвижения автомобиля, если он проехал 100 км за 1 час 30 минут. Сначала требуется перевести 1 час 30 минут в часы, так как в большинстве случаев единицей измерения рассматриваемого параметра считается километр в час (км/ч). Итак, 1 час 30 минут равно 1,5 часа, потому что 30 минут есть половина или 1/2 или 0,5 часа. Сложив вместе 1 час и 0,5 часа получим 1,5 часа.
Теперь нужно подставить имеющиеся значения вместо буквенных символов:
v=100 км/1,5 ч=66,66 км/ч
Здесь v=66,66 км/ч, и это значение очень приблизительное (незнающим людям об этом лучше прочитать в специальной литературе), S=100 км, t=1,5 ч.
Таким нехитрым способом можно найти скорость через время и расстояние.
А что делать, если нужно найти среднее значение? В принципе, вычисления, показанные выше, и дают в итоге результат среднего значение искомого нами параметра. Однако можно вывести и более точное значение, если известно, что на некоторых участках по сравнению с другими скорость объекта была непостоянной. Тогда пользуются таким видом формулы:
vср=(v1+v2+v3+…+vn)/n, где v1, v2, v3, vn — значения скоростей объекта на отдельных участках пути S, n — количество этих участков, vср — средняя скорость объекта на всем протяжении всего пути.
Эту же формулу можно записать иначе, используя путь и время, за которое объект прошел этот путь:
- vср=(S1+S2+…+Sn)/t, где vср — средняя скорость объекта на всем протяжении пути,
- S1, S2, Sn — отдельные неравномерные участки всего пути,
- t — общее время, за которое объект прошел все участки.
Можно записать использовать и такой вид вычислений:
- vср=S/(t1+t2+…+tn), где S — общее пройденное расстояние,
- t1, t2, tn — время прохождения отдельных участков расстояния S.
Но можно записать эту же формулу и в более точном варианте:
vср=S1/t1+S2/t2+…+Sn/tn, где S1/t1, S2/t2, Sn/tn — формулы вычисления скорости на каждом отдельном участке всего пути S.
Таким образом, очень легко найти искомый параметр, используя данные выше формулы. Они очень просты, и как уже было указано, используются в начальных классах. Более сложные формулы базируются на этих же формулах и на тех же принципах построения и вычисления, но имеют другой, более сложный вид, больше переменных и разных коэффициентов. Это нужно для получения наиболее точного значения показателей.
Видео
Молекулярная физика
К оглавлению…
Химическое количество вещества находится по одной из формул:
Масса одной молекулы вещества может быть найдена по следующей формуле:
Связь массы, плотности и объёма:
Основное уравнение молекулярно-кинетической теории (МКТ) идеального газа:
Определение концентрации задаётся следующей формулой:
Для средней квадратичной скорости молекул имеется две формулы:
Средняя кинетическая энергия поступательного движения одной молекулы:
Постоянная Больцмана, постоянная Авогадро и универсальная газовая постоянная связаны следующим образом:
Следствия из основного уравнения МКТ:
Уравнение состояния идеального газа (уравнение Клапейрона-Менделеева):
Газовые законы. Закон Бойля-Мариотта:
Закон Гей-Люссака:
Закон Шарля:
Универсальный газовый закон (Клапейрона):
Давление смеси газов (закон Дальтона):
Тепловое расширение тел. Тепловое расширение газов описывается законом Гей-Люссака. Тепловое расширение жидкостей подчиняется следующему закону:
Для расширения твердых тел применяются три формулы, описывающие изменение линейных размеров, площади и объема тела:
Единицы измерения времени
Основной единицей измерения момента силы в системах СИ и СГС является: [t]=c
Единицы измерения времени основываются на периоде вращения Земли около своей оси и вокруг Солнца, Луни вокруг Земли. Внесистемные единицы измерения времени: час, минута, сутки и т.д.
Скорость
Двигаться со скоростью черепахи — значит медленно, а со скоростью света — значит очень быстро. Сейчас узнаем, как пишется скорость в математике и как ее найти по формуле.
Скорость определяет путь, который преодолеет объект за единицу времени. Скорость обозначается латинской буквой v.
Проще говоря, скоростью называют расстояние, пройденное телом за единицу времени.
Впервые формулу скорости проходят на математике в 5 классе. Сейчас мы ее сформулируем и покажем, как ее использовать.
Формула скорости
Чтобы найти скорость, нужно разделить путь на время:
v = s : t
Показатели скорости чаще всего выражаются в м/сек или км/час.
Скорость сближения — это расстояние, на которое сблизились два объекта за единицу времени. Чтобы найти скорость сближения двух объектов, которые движутся навстречу друг другу, надо сложить скорости этих объектов.
Скорость удаления — расстояние, на которое отдалились друг от друга два объекта за единицу времени.
Чтобы найти скорость удаления объектов, которые движутся в противоположных направлениях, нужно сложить скорости этих объектов.
Чтобы найти скорость удаления при движении с отставанием или скорость сближения при движении вдогонку, нужно из большей скорости вычесть меньшую.
Онлайн-курсы по математике для детей — отличный способ разобраться в сложных темах под руководством внимательного преподавателя.
Формулы для расчета пути и времени движения при неравномерном движении тела
При неравномерном движении мы используем определение средней скорости, которую можем найти по формуле
$$upsilon_{ср} = frac{S}{t}$$
Чтобы определить путь при неравномерном движении, нужно среднюю скорость движения умножить на время:
$$large S = upsilon_{ср} t$$
Также мы можем рассчитать время, разделив путь, пройденный телом, на среднюю скорость его движения:
$$t = frac{s}{upsilon_{ср}}$$
Импульс
К оглавлению…
Импульс тела находится по следующей формуле:
Изменение импульса тела или системы тел (обратите внимание, что разность конечного и начального импульсов векторная):
Общий импульс системы тел (важно то, что сумма векторная):
Второй закон Ньютона в импульсной форме может быть записан в виде следующей формулы:
Закон сохранения импульса. Как следует из предыдущей формулы, в случае если на систему тел не действует внешних сил, либо действие внешних сил скомпенсировано (равнодействующая сила равна нолю), то изменение импульса равно нолю, что означает, что общий импульс системы сохраняется:
Если внешние силы не действуют только вдоль одной из осей, то сохраняется проекция импульса на данную ось, например:
Самая большая единица измерения времени
Самая большая единица измерения времени – кальпа. Кальпа является понятием из индуизма и буддизма. Она равняется примерно 4,32 миллиардам лет, что совпадает с возрастом Земли с точностью до 5%.
Как в голову древним индуистам пришли такие цифры? Ответа на этот вопрос мы не знаем, но вся система как будто говорит нам, что тогда люди знали о Вселенной немного больше, чем мы.
Кальпу в индуизме еще называют «днем Брахмы». День сменяется ночью, равной ему по продолжительности. 30 дней и ночей составляют месяц, а год состоит из 12 месяцев. Вся жизнь Брахмы – 100 лет, по прошествии которых мир погибает вместе с ним.
Если перевести сто лет Брахмы в наши традиционные годы, получится 311 триллионов и 40 миллиардов лет! Нынешнему Брахме 51 год.
Вывод: если все это правда, то беспокоится не стоит — Вселенная будет существовать еще долгое время.
Основные формулы электричества
Для многих студентов тема про электричество сложнее, чем про термодинамика, но она не менее важна. Итак, начнём с электростатики:
Переходим к постоянному электрическому току:
Далее добавляем формулы по теме: “Магнитное поле электрического тока”
Электромагнитная индукция тоже важная тема для знания и понимания физики. Конечно, формулы по этой теме необходимы:
Ну и, конечно, куда же без электромагнитных колебаний:
График пути равномерного движения
Пример графика зависимости пути равномерного движения представлен на рисунке 3.
Здесь $S$ — ось пройденных путей, $t$ — ось времени. По этому графику мы можем найти путь, пройденный телом за определенный промежуток времени. Например, за 1 с тело проходит путь длиной 2 м, за 2 с – 4 м, за 3 с – 6 м.
Зная путь и время, мы можем рассчитать скорость. Для удобства расчета возьмем самый первый отрезок пути: $t = 1 с, s = 2 м$. Тогда,
$upsilon = frac{s}{t} = frac{2 м}{1 с} = 2 frac{м}{с}$.
Решение задач
Понять действие формул времени при равномерном движении или равноускоренном можно, решив задачу. Многие сайты предлагают онлайн-калькулятор для удобного подсчета. В соответствующие графы достаточно ввести основные данные, после чего программа рассчитает все самостоятельно.
Задача 1. Автомобиль ехал со скоростью 200 км/ч и проехал всего 80 км. Требуется определить время движения машины. Условные обозначения:
- V — скорость;
- S — расстояние;
- t — время.
Показатели нужно перевести из километров в метры, из часов в секунды: 1 км = 1 тыс. м, 1 час = 3600 секунд. Получаем S = 80000 м, V= 200000/3600 = 55,55 м/с. Находим скорость по формуле: V= S/t = 80000/55,55 = 1440,14 сек.
t = 1440
14/3600 = 0,4 часа.
Ответ: автомобиль пройдет 0,4 ч.
При неравномерном движении путь, пройденный телом, равен произведению средней скорости на время, в течение которого тело перемещалось.
Задача 2. Движение точки задано уравнением: х = 2t — 0,03t2. Нужно определить, в какой период скорость точки сближения сравняется с нулевой отметкой. Коэффициенты равны 2м/с, 0,03 м/с2.
Условия задачи содержат функцию x (t). Скорость можно вычислить по формуле V = dx/dt = 2 — 0,06t Приравниваем скорость к 0, находим t:
2 — 0,06t = 0
t = 2/0,06 = 33,33 сек.
Необходимо определить зависимость модуля ускорения от времени: A (t)= dv/dt = -0,06.
Задача 3. Самолет для взлета набирает 350 км/ч. Нужно определить время разгона, если скорость достигается в конце взлетной полосы длиной в 2 км. Движение считается равноускоренным.
При равноускоренном движении формула выглядит как S = V0t+at2/2. При этом V= V0+at. Разгон самолета начинается с состояния покоя, то есть V0 = 0.
S = at2/2
V=at.
S = (V/t)*(t2/2) = Vt/2.
S = 2000 м
V=350 км/ч = 97,2 м/с.
t= 2S/V = 2*2000/97,2 = 41,15.
Благодаря вычислению известно, что разгон самолета длится 41,15 сек.
Задача 4. Скорость конькобежца составляет 15 м/с. Нужно вычислить время, за которое он пробежит путь 3 км.
V= 15 м/с.
S = 3 км (3000 м).
t = S/V = 3000/15 = 200
Ответ: за 200 секунд конькобежец пробежит 3 км.
Современная наука распределяет известные представления о времени в разные концепции — относительную и вещественную. По мнению относительной, в природе не существует временных рамок, а понятие времени является отношением между событиями. Время — проявление свойств физических тел и изменений, оно статично, как и пространство.
Теги
С древних времен людей беспокоит мысль о достижении сверх скоростей, так же как не дают покоя раздумья о высотах, летательных аппаратах. На самом деле это два очень сильно связанных между собой понятия. То, насколько быстро можно добраться из одного пункта в другой на летательном аппарате в наше время, зависит полностью от скорости. Рассмотрим же способы и формулы расчета этого показателя, а также времени и расстояния.
Как же рассчитать скорость?
На самом деле, рассчитать ее можно несколькими способами:
- через формулу нахождения мощности;
- через дифференциальные исчисления;
- по угловым параметрам и так далее.
В этой статье рассматривается самый простой способ с самой простой формулой — нахождение значения этого параметра через расстояние и время. Кстати, в формулах дифференциального расчета также присутствуют эти показатели. Формула выглядит следующим образом:
v=S/t, где
- v — скорость объекта,
- S — расстояние, которое пройдено или должно быть пройдено объектом,
- t — время, за которое пройдено или должно быть пройдено расстояние.
Как видите, в формуле первого класса средней школы нет ничего сложного. Подставив соответствующие значения вместо буквенных обозначений, можно рассчитать быстроту передвижения объекта. Например, найдем значение скорости передвижения автомобиля, если он проехал 100 км за 1 час 30 минут. Сначала требуется перевести 1 час 30 минут в часы, так как в большинстве случаев единицей измерения рассматриваемого параметра считается километр в час (км/ч). Итак, 1 час 30 минут равно 1,5 часа, потому что 30 минут есть половина или 1/2 или 0,5 часа. Сложив вместе 1 час и 0,5 часа получим 1,5 часа.
Теперь нужно подставить имеющиеся значения вместо буквенных символов:
v=100 км/1,5 ч=66,66 км/ч
Здесь v=66,66 км/ч, и это значение очень приблизительное (незнающим людям об этом лучше прочитать в специальной литературе), S=100 км, t=1,5 ч.
Таким нехитрым способом можно найти скорость через время и расстояние.
А что делать, если нужно найти среднее значение? В принципе, вычисления, показанные выше, и дают в итоге результат среднего значение искомого нами параметра. Однако можно вывести и более точное значение, если известно, что на некоторых участках по сравнению с другими скорость объекта была непостоянной. Тогда пользуются таким видом формулы:
vср=(v1+v2+v3+…+vn)/n, где v1, v2, v3, vn — значения скоростей объекта на отдельных участках пути S, n — количество этих участков, vср — средняя скорость объекта на всем протяжении всего пути.
Эту же формулу можно записать иначе, используя путь и время, за которое объект прошел этот путь:
- vср=(S1+S2+…+Sn)/t, где vср — средняя скорость объекта на всем протяжении пути,
- S1, S2, Sn — отдельные неравномерные участки всего пути,
- t — общее время, за которое объект прошел все участки.
Можно записать использовать и такой вид вычислений:
- vср=S/(t1+t2+…+tn), где S — общее пройденное расстояние,
- t1, t2, tn — время прохождения отдельных участков расстояния S.
Но можно записать эту же формулу и в более точном варианте:
vср=S1/t1+S2/t2+…+Sn/tn, где S1/t1, S2/t2, Sn/tn — формулы вычисления скорости на каждом отдельном участке всего пути S.
Таким образом, очень легко найти искомый параметр, используя данные выше формулы. Они очень просты, и как уже было указано, используются в начальных классах. Более сложные формулы базируются на этих же формулах и на тех же принципах построения и вычисления, но имеют другой, более сложный вид, больше переменных и разных коэффициентов. Это нужно для получения наиболее точного значения показателей.
Другие способы вычисления
Существую и другие способы и методы, которые помогают вычислить значения рассматриваемого параметра. В пример можно привести формулу вычисления мощности:
N=F*v*cos α , где N — механическая мощность,
F — сила,
v — скорость,
cos α — косинус угла между векторами силы и скорости.
Способы вычисления расстояния и времени
Можно и наоборот, зная скорость, найти значение расстояния или времени. Например:
S=v*t, где v — понятно что такое,
S — расстояние, которое требуется найти,
t — время, за которое объект прошел это расстояние.
Таким образом вычисляется значение расстояния.
Или вычисляем значение времени, за которое пройдено расстояние:
t=S/v, где v — все та же скорость,
S — расстояние, пройденный путь,
t — время, значение которого в данном случае нужно найти.
Для нахождения средних значений этих параметров существует довольно много представлений как данной формулы, так и всех остальных. Главное, знать основные правила перестановок и вычислений. А еще главнее знать сами формулы и лучше наизусть. Если же запомнить не получается, тогда лучше записывать. Это поможет, не сомневайтесь.
Пользуясь такими перестановками можно с легкостью найти время, расстояние и другие параметры, используя нужные, правильные способы их вычисления.
И это еще не предел!
Видео
В нашем видео вы найдете интересные примеры решения задач на нахождение скорости, времени и расстояния.
«Формула времени. Решение задач»
Скорость, время и расстояние — физические величины, взаимосвязаны процессом движения. Виды движений: 1) равномерное (прямолинейное, криволинейное и по окружности), 2) равноускоренное (с постоянным ускорением), 3) гармоническое. Для каждого вида движения своя формула времени.
Время обозначается как t. Единица измерения времени – с (секунды).
Самая простая формула при равномерном прямолинейном движении. Время, необходимое для прохождения пути равняется частному от деления пути на скорость равномерного прямолинейного движения: t = S / v.
При равноускоренном движении время равняется частному от деления разницы конечной и начальной скорости на ускорение: t = (v — v0) / a или частному от деления пути на разность конечной и начальной скорости: t = S / (v — v0).
Решение задач через формулу времени
Задача № 1.
Конькобежец может развивать скорость до 13 м/с. За какое время он пробежит дистанцию длиной 2,6 км?

Задача № 2.
Двигаясь с ускорением 5 м/с2 скорость космической ракеты увеличилась на 100 м/с. За какое время произошло такое изменение скорости?
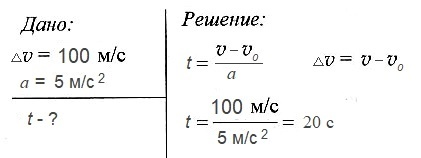
Задача № 3.
Пункты А и В находятся на берегу реки на некотором расстоянии друг от друга. Моторная лодка проходит расстояние АВ вниз по течению реки за время t1 = 3 ч, а плот то же расстояние – за время t0 =12 ч. Какое время t2 затратит моторная лодка на обратный путь?
Решение. Обозначим расстояние между пунктами А и В через L, скорость моторной лодки относительно воды через vл , а скорость течения через vт. Тогда t0 = L / vт , t1 = L / (vл + vт) , t2 = L / (vл — vт) . Исключая из записанной системы уравнений L, vл и vт
находим
Ответ: 6 ч.
Конспект урока «Формула времени. Решение задач».
Следующая тема: «».
Содержание:
- Определение и формула времени
- Особенности времени как физической величины
- Особенности времени как физической величины
- Единицы измерения времени
- Примеры решения задач
Определение и формула времени
В понятие времени отражаются такие свойства мира как постоянное развитие, изменение его в сознании человека. Процессы идут в определенной последовательности, при этом имеют определённую продолжительность.
Определение
Время – физическая величина, отражающая свойство материальных процессов иметь определенную продолжительность,
следовать друг за другом в установленной последовательности и развиваться этапно. Обозначают время буквой t.
Особенности времени как физической величины
Время неотделимо от материи и ее движения, так как является ее формой существования. Нет смысла говорить о времени самом по себе, так как в отрыве от материальных процессов течение времени становится бессодержательным. Только исследование процессов, происходящих в материальном мире и их взаимосвязей, делает понятие времени физически содержательным.
В череде процессов, происходящих в природе, особенное место занимают повторяющиеся процессы (повторение дней и ночей, дыхание, перемещение звезд по небосводу и т. д). Исследование и сравнение подобных процессов между собой ведет к идее о длительности материальных процессов, сравнение их длительности приводит к идее об их измерении.
Эталоном измерения является периодический процесс, который называют часами. Существуют системы отсчета, в которых возможно введение единого времени с достаточной для практики точностью. Введение единого времени хорошо подтверждается экспериментом. Теория дает возможность предсказать отклонения единого времени, что можно проверить эмпирически.
Длительность физического процесса, который происходит в некоторой точке, определяют при помощи часов, которые располагают в той же точке. При этом применяется прямое сравнение, сравниваются длительности процессов, которые текут в одной точке. Измерение длительности сводят к фиксации начала и окончания рассматриваемого процесса на шкале процесса, который принимают за эталонный. При этом говорят как о фиксации показаний часов в момент начала и окончания процесса, и это не имеет отношения к фактическому месту нахождения часов (процесса) в точке рассмотрения.
Синхронизация часов и изучения законов распространения физических сигналов развивались параллельно, при этом происходили взаимные уточнения и дополнения. Синхронизацию проводят при помощи сигналов, которые распространяются с конечной скоростью. Этот метод использует определение постоянной скорости: если из точки, в которой часы показывают t0, исходит сигнал, перемещающийся со скоростью v=const, то тогда, когда сигнал придет в точку на расстоянии s, часы в этой точке должны показать время:
$$t=t_{0}+frac{s}{v}(1)$$
Такая синхронизация согласуется с синхронизацией с использованием световых сигналов. Тогда часы синхронизируются по формуле:
$$t=t_{0}+frac{s}{c}(2)$$
где c=299792,4562 км/с – скорость света, которая не зависит от скорости источника и приемника по всем направлениям пространства одинакова.
Особенности времени как физической величины
Перемещение ($bar{s}$), равно:
$$bar{s}left(t_{2}, t_{1}right)=bar{s}left(t_{2}right)-bar{s}left(t_{1}right)(3)$$
где $bar{s}(t_2)$ – радиус-вектор в момент времени
$t_2, bar{s}(t_1)$ – радиус-вектор в момент времени
$t_1$ .
Мгновенная скорость ($bar{v}$):
$$bar{v}=frac{d bar{s}}{d t}(4)$$
Мгновенное ускорение ($bar{a}$):
$$bar{a}=frac{d bar{v}}{d t}(5)$$
Единицы измерения времени
Основной единицей измерения момента силы в системах СИ и СГС является: [t]=c
Единицы измерения времени основываются на периоде вращения Земли около своей
оси и вокруг Солнца, Луни вокруг Земли. Внесистемные единицы измерения времени: час, минута, сутки и т.д.
Примеры решения задач
Пример
Задание. Движения двух тел заданы уравнениями: и s1(t)=5t и s2(t)=150-10t. Найдите время встречи.
Решение. В точке встречи s1(t)=s2(t). Приравняем правые части функцийx(t), имеем:
$$5 t=150-10 t rightarrow 15 t=150 rightarrow t=10$$
Ответ. t=10 c

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Движение материальной точки, задано уравнением: x=4t-0,05t2 .
В какой момент времени, скорость точки равна нулю? Коэффициенты имеют размерности: 4 м/с, 0,05м/с2 .
Изобразите графики зависимости модуля ускорения от времени.
Решение. В условиях задачи задана функция x(t), скорость можно найти как:
$$v=frac{d x}{d t}=4-0,1 t(2.1)$$
Приравняем скорость к нулю, найдем время:
$$4-0,1 t=0 rightarrow t=frac{4}{0,1}=40(c)$$
Определим, какова зависимость модуля ускорения от времени, для этого возьмем производную по времени от функции v(t) (2.1):
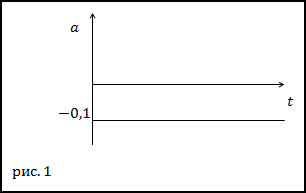
$$a(t)=frac{d v}{d t}=-0,1(2.2)$$
Тогда график зависимости a(t) имеет вид:
Ответ. t=40 c
Читать дальше: Формула длины волны.