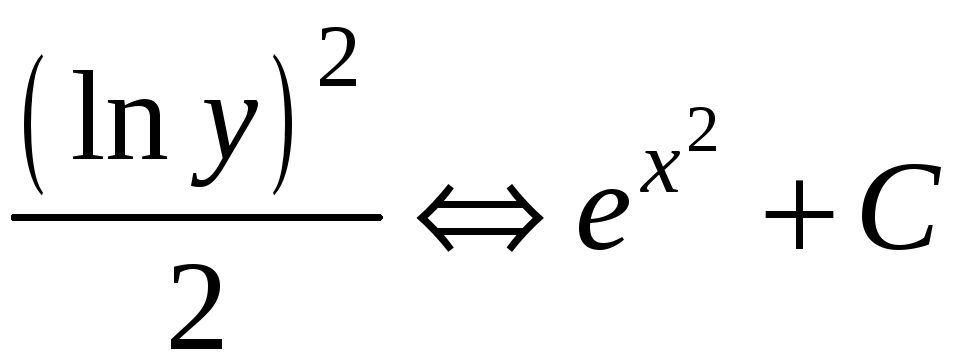1. Уравнения с разделяющимися переменными
Общий вид уравнений
. (8.10)
С учетом равенства
(8.11)
уравнение (8.10) может быть записано в виде 
.
Разделим обе части на произведение функций M(x)∙Q(y) (при условии 
) и после сокращения получим: 
. Так как переменные разделены, проинтегрируем уравнение
почленно:
. После нахождения интегралов получаем общий интеграл
исходного ДУ. Предполагая, что
, мы могли потерять решения. Следовательно, необходимо
подстановкой M(x)=0, Q(y)=0 в исходное уравнение сделать проверку. В том
случае, когда данные функции удовлетворяют уравнению, они также являются его решениями.
Пример 8.2. Проинтегрировать уравнение 
.
Решение. Представим уравнение в виде
. Разделим переменные: 
. Проинтегрируем уравнение:
.
После
применения теоремы о сумме логарифмов и потенцирования получаем
– общий интеграл исходного уравнения
2.
Однородные дифференциальные уравнения первого порядка
Общий вид уравнений
, (8.12)
где M(x;y) и N(x;y)– однородные функции аргументов x и y одного и
того же измерения m, то есть
имеют место равенства
. (8.13)
Метод решения уравнения (8.12) – деление на переменную
x в
степени измерения m: 
. Далее уравнение преобразуются с помощью следующей замены:
. (8.14)
Однородное уравнение (8.12) принимает вид: 
– уравнение с
разделяющимися переменными. Следовательно, дальнейшее решение – по пункту 1.
Пример 8.3. Проинтегрировать уравнение 
.
Решение. Поделим уравнение на x2, получим
. После замены (8.14) заданное по условию уравнение принимает
вид 
,
. В результате интегрирования получим 
. После обратной замены 
– искомый общий
интеграл
Пример 8.4. Найти общее решение
(общий интеграл) дифференциального уравнения 
.
Решение. Правая часть уравнения 
обладает свойством 
. Поэтому заданное
уравнение является однородным дифференциальным уравнением первого порядка.
Совершим замену 
, где u – некоторая
функция от аргумента x. Отсюда
. Исходное уравнение приобретает вид
или 
. Разделим переменные: 
.
После
интегрирования обеих частей уравнения получаем
. Таким образом,
.
Потенцируя,
находим 
.
Итак,
общий интеграл исходного уравнения приобретает вид cy=x2+y2, где c – произвольная
постоянная
3. Дифференциальные уравнения первого порядка, приводящиеся к однородным или к уравнениям с разделяющимися переменными
Общий вид уравнений
, (8.15)
где
– числа.
При c1=c2=0 уравнение
является однородным. Рассмотрим два случая при c1 и c2 не равных нулю одновременно.
1) Определитель
. Вводят новые переменные u и v, положив x=u+x0, y=v+y0, где (x0;y0) – решение системы уравнений
.
В результате данной подстановки уравнение (8.15)
становится однородным.
Пример 8.5. Найти общее решение
(общий интеграл) дифференциального уравнения 
.
Решение. Определитель 
, следовательно,
решаем систему уравнений 
. Получаем значения x0= –1; y0=2, с
использованием которых осуществляем
замену x=u–1;y=v+2, при этом 
. Заданное по условию
ДУ принимает вид:
, (*) – однородное ДУ относительно функции v и переменной u.
Обозначим 
. Уравнение (*) принимает вид: 
. Продолжим преобразования:
. Проинтегрируем уравнение:
С помощью формул
интегрирования (4.8) и (4.17) получаем:
.
Осуществим обратную
подстановку
:
– общий интеграл исходного уравнения
2) Определитель
. Это означает пропорциональность коэффициентов 
или
. Уравнение (8.15) принимает вид: 
. С помощью замены
, оно приводится к
уравнению с разделяющимися переменными вида 
.
Пример 8.6. Найти общее решение
(общий интеграл) дифференциального уравнения
.
Решение. Определитель 
, следовательно, осуществляем замену
.
Исходное
уравнение принимает вид:
или 
.
Далее 
. Разделим переменные: 
или 
. Проинтегрируем уравнение:
.
После обратной замены получим: 
– общий интеграл
исходного уравнения
4.
Линейные дифференциальные уравнения первого порядка
Общий вид уравнений
, (8.16)
где
P(x) и Q(x) –
заданные функции (могут быть постоянными).
Уравнение (8.16) может быть решено двумя способами.
1) Метод Бернулли-Фурье состоит в том,
что решение ищется в виде произведения двух неизвестных функций y(x)=u(x)∙v(x) или коротко y=u∙v, при этом 
. Одна из функций будет представлять общую часть решения и
содержать константу интегрирования c, другая функция может быть взята в частном виде при
конкретном значении константы (общее решение ДУ первого порядка должно содержать
одну константу интегрирования). Подставим выражения y и 
в (8.16), после чего
оно принимает вид:
. (8.17)
Функцию v(x) подберем в частном виде так, чтобы выражение в
скобках обратилось в ноль. Для этого решим уравнение с разделяющимися
переменными 
или 
. Отсюда в результате интегрирования получим: 
. Так функция v(x) выбиралась произвольно, то можно положить c = 1, тогда 
. Подставив найденную v(x) в (8.17), приходим к еще одному уравнению с
разделяющимися переменными 
. Интегрируя его, получим функцию 
. Общее решение исходного ДУ (8.16) принимает вид
. (8.18)
Пример 8.7. Проинтегрировать уравнение 
с помощью метода
Бернулли.
Решение. Данное уравнение является линейным ДУ первого порядка с
функциями 
. Применим подстановку
y=u∙v, где u и v – некоторые функции аргумента x. Так
как y=u∙v, 
то , и заданное уравнение принимает вид:
.
(**)
Выберем функцию u так, чтобы выражение, стоящее в скобках, обращалось в ноль, то есть 
или
.
Полагая c=1, получим
u=cos x.
При таком выборе функции u уравнение
(**) примет вид:
. Отсюда v=tg x+c. Тогда 
– общее решение
заданного уравнения.
Общее решение заданного ДУ можно также получить,
пользуясь непосредственно формулой (8.18):
.
По условию задачи имеем: P(x)=tg x, 
. Следовательно, 
. Так как
, то с использованием основного логарифмического тождества
получаем:
.
Таким образом, 
– общее решение исходного дифференциального
уравнения
2) Метод Лагранжа иначе называют методом вариации произвольной постоянной.
Рассмотрим сначала соответствующее линейное однородное ДУ первого порядка, то есть
исходное уравнение без правой части 
. Разделив переменные и проинтегрировав, в найденном решении
полагают постоянную c функцией c(x). После этого функцию y дифференцируют и вместе с подставляют в исходное
уравнение. При этом получают уравнение относительно неизвестной функции c(x), отыскав
которую, подставляют ее в y – общее решение заданного линейного неоднородного
уравнения (с правой частью).
Пример 8.8. Проинтегрировать уравнение с помощью метода
Лагранжа (сравни с примером 8.7).
Решение. Решим сначала соответствующее линейное однородное ДУ
первого порядка 
или 
. Разделим переменные: 
. В результате интегрирования получаем: 
– общее решение
соответствующего однородного уравнения. Применим метод варьирования константы,
то есть предположим c=c(x). Тогда общее решение исходного линейного
неоднородного уравнения будет иметь вид: 
. Подставим y и в исходное уравнение:
. После сокращений получим:
. Разделим переменные и проинтегрируем: 
.
Подставляя найденное c(x) в y, имеем общее решение линейного неоднородного
уравнения:
5.
Уравнения Бернулли
Общий вид уравнений
. (8.19)
При n=1 (8.19)– уравнение с разделяющимися переменными. При n=0 (8.19)– линейное ДУ.
Рассмотрим 
. Метод решения – деление уравнения на 
, после чего (8.19) принимает вид 
.
С помощью замены z=y–n+1
исходное уравнение становится линейным относительно функции z(x):
, (8.20)
то есть его решение находится аналогично пункту 4. На
практике искать решение уравнения (8.17) удобнее методом Бернулли в виде
произведения неизвестных функций y=u∙v. Заметим, что y=0 – всегда является решением исходного уравнения
(8.17).
Пример 8.9. Проинтегрировать уравнение 
.
Решение. Заданное
уравнение является уравнением Бернулли. Положим y=u∙v, тогда 
и уравнение примет
вид:
.
Выберем функцию u так, чтобы выполнялось равенство:
. Разделим переменные и
проинтегрируем:
. При c=1 получим функцию
.
Тогда заданное уравнение после сокращения на u примет
вид: 
или 
– уравнение
с разделяющимися переменными. Находим его общее решение:
. Интегрируя последнее уравнение,
получим:
. Следовательно, общее решение заданного уравнения имеет вид:
6. Уравнения
в полных дифференциалах
6.1. Общий вид уравнений
, (8.21)
где
левая часть есть полный дифференциал некоторой функции F(x;y), то есть 
. В этом случае ДУ (8.21) можно записать в виде
, а его общий интеграл будет F(x;y)=c.
Условие, по которому можно судить, что выражение 
является полным
дифференциалом, можно сформулировать в виде следующей теоремы.
Теорема 8.2.
Для того чтобы выражение , где функции M(x;y) и N(x;y), их частные
производные 
и 
непрерывны в некоторой
области D плоскости x0y, было
полным дифференциалом, необходимо и
достаточно выполнение условия
(8.22)
Таким образом, согласно определению полного
дифференциала (6.6) должны выполняться равенства:
. (8.23)
Формула (8.22) представляет собой теорему Шварца,
согласно которой смешанные производные второго порядка функции F(x;y) равны.
Зафиксируем переменную y и проинтегрируем первое уравнение из (8.23) по x, получим:
. (8.24)
Здесь
мы применили метод вариации произвольной постоянной, так как предположили, что
константа c зависит от y (либо
является числом). Продифференцировав (8.24) по переменной y
и приравняв производную к функции N(x;y), мы получим уравнение для нахождения неизвестной c(y).
Подставив c(y) в (8.24), находим функцию F(x;y) такую, что
.
Пример 8.10. Решить
уравнение 
.
Решение. Здесь функция 
.
Проверим условие (8.22): 
. Следовательно, левая часть заданного уравнения представляет собой полный дифференциал
некоторой функции F(x;y). Для ее
отыскания проинтегрируем функцию M(x;y) по
переменной x, считая y=const:
.
Пусть c=c(y),
тогда 
. Продифференцируем данную функцию по y,
получим 
. Отсюда 
.
Найденное c(y) подставляем в функцию F(x;y), получаем
решение заданного ДУ:
Если условие (8.22) не выполняется, то ДУ (8.21) не
является уравнением в полных дифференциалах.
Однако это уравнение иногда можно привести к уравнению
в полных дифференциалах умножением его на некоторую функцию μ(x;y), называемую интегрирующим множителем.
Чтобы уравнение 
было уравнение в полных
дифференциалах, должно выполняться условие
. (8.25)
Выполнив дифференцирование 
и приведя подобные
слагаемые, получим: 
. Для нахождения μ(x;y) надо
проинтегрировать полученное ДУ в частных производных. Решение этой задачи не
простое. Нахождение интегрирующего множителя может быть упрощено, если
допустить существование μ как функции только одного аргумента x либо
только y.
6.2. Пусть μ = μ(x). Тогда уравнение (8.25) принимает вид:
(8.26)
При этом подынтегральное выражение должно зависеть только от x.
6.3. Пусть
μ = μ(y). Тогда
аналогично можно получить
, (8.27)
где подынтегральное выражение должно зависеть только
от y.
Пример 8.11. Решить
уравнение 
.
Решение. Здесь 
, то есть 
. Проверим существование интегрирующего множителя. По
формуле (8.26) составляем подынтегральное выражение:
, оно зависит только от
переменной x. Следовательно, уравнение имеет интегрирующий
множитель μ(x). В нашем
случае он имеет вид 
. Умножая исходное уравнение на
μ=x, получаем: 
, то есть уравнение в полных дифференциалах. Действительно, для него
. Решив его аналогично пункту 6.1, найдем, что общий
интеграл исходного уравнения имеет вид 
7. Дифференциальные уравнения, неразрешенные относительно производной
К уравнениям данного вида относятся уравнения Лагранжа и Клеро, которые образуют достаточно большой класс ДУ, решаемых методом введения параметра 
.
7.1.
Уравнение Лагранжа
Общий вид уравнений
, (8.28)
где
φ
и ψ– известные функции от 
. После введения параметра 
уравнение (8.28)
принимает вид
. (8.29)
Продифференцируем его по x:
. (8.30)
Полученное уравнение (8.30) является линейным уравнением относительно
неизвестной функции x = x(p). Решив
его, найдем:
x = λ(p;c). (8.31)
Исключая параметр p из уравнений
(8.29) и (8.31), получаем общий
интеграл уравнения (8.28) в
виде y = γ(x;c).
Примечание. При переходе к уравнению (8.30) мы делили на 
. При этом могли быть потеряны решения, для которых 
или p = p0=const. Это
означает, что p0 является
корнем уравнения p = φ(p)=0 (смотри уравнение (8.30)). Тогда
решение 
для уравнения (8.28)
является особым
7.2. Уравнение
Клеро представляет собой частный случай уравнения Лагранжа
при 
, следовательно, его общий вид
. (8.32)
Вводим
параметр , после чего уравнение (8.30) записывается так:
. (8.33)
Продифференцируем уравнение (8.33) по переменной x:
,
то согласно (8.33), уравнение (8.32) имеет общее решение
. (8.34)
При 
получаем частное решение уравнения
в параметрической форме:
.
(8.35)
Это – особое решение уравнения Клеро, так как оно не
содержится в формуле общего решения уравнения.
Пример 8.12.
Решить уравнение Клеро 
.
Решение. Согласно формуле (8.32) общее решение имеет вид y=cx+c2. Особое решение уравнения получим по (8.33) в виде
. Отсюда следует: 
, то есть 
Вопросы для самопроверки
Найти общий интеграл дифференциального уравнения
Общий интеграл дифференциального уравнения записывается следующим образом $$F(x,y)=С.$$
| Пример 1 |
| Найти общий интеграл дифференциального уравнения первого порядка $$(x^2 y + y)dy = sqrt{4+y^2}dx.$$ |
| Решение |
|
Перед нами уравнение с разделяющимися переменными. То есть можно отделить $y$ от $x$ по разные стороны уравнения. Для этого видим, что можно в левой части уравнения вынести за скобку $y$. Затем разделим обе части уравнения на скобку и корень. $$y(x^2+1)dy=sqrt{4+y^2}dx,$$ $$frac{ydy}{sqrt{4+y^2}}=frac{dx}{x^2+1}$$ Теперь нужно проинтегрировать обе части уравнения. Для этого необходимо использовать таблицу интегрирования основных элементарных функций. Для правой части преобразований делать не нужно, можно сразу взять данные из таблицы. А вот левую часть нужно преобразовать в подходящий вид. Для этого выполним подведение под знак дифференциала числитель. $$int frac{d(4+y^2)}{2sqrt{4+y^2}} = arctg x + C$$ Теперь левую часть можно легко проинтегрировать, зная, что $(sqrt{x})’ = frac{1}{2sqrt{x}}$. Получаем $$sqrt{4+y^2} = arctg x + C.$$ И вот теперь мы подошли к самому главному. Вытащить $y$ из под корня или нет? Так как общий интеграл дифференциального уравнения выглядит следующим образом $F(x,y)=С$, то достаточно перенести арктангенс из правой части равенства в левую $$sqrt{4+y^2}-arctg x = C.$$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$sqrt{4+y^2}-arctg x = C$$ |
| Пример 2 |
| Найти общий интеграл однородного дифференциального уравнения $(x^2+y^2)dx-xydy=0$. |
| Решение |
|
Для начала убеждаемся, что уравнение однородное. Для этого подставляем $lambda$ перед всеми $x$ и $y$. Для подтверждения однородности все $lambda$ должны сократиться и уравнение примет исходный вид. $$((lambda x)^2 + (lambda y)^2) dx — lambda x lambda y dy = 0,$$ $$lambda^2 (x^2 + y^2) dx — lambda^2 xy dy = 0,$$ $$(x^2+y^2)dx — xydy = 0.$$ Далее начинаем решение уравнения с подстановки $y = tx$, $y’ = t’x+t$. Но заметим, что $y’ = frac{dy}{dx}$. Получаем $$(x^2+t^2x^2)-x^2 t (t’x+t)=0,$$ $$x^2 + t^2 x^2 — t’tx^3 — t^2 x^2=0,$$ $$x^2 — t’tx^3=0.$$ После раскрытия скобок и сокращения подобных получили дифференциальное уравнение с разделяющимися переменными. Выполняем разделение переменных $t$ и $x$ по левой и правой частям уравнения. $$t’tx^3 = x^2,$$ $$t’t = frac{1}{x},$$ $$tfrac{dt}{dx} = frac{1}{x}, $$ $$tdt = frac{dx}{x}.$$ Далее теперь можно проинтегрировать обе части уравнения. Для этого используем таблицу интегралов. $$int t dt = int frac{dx}{x},$$ $$frac{t^2}{2} = ln|x| + C,$$ $$t^2 = 2ln|x|+C.$$ Выполняем обратную замену $t = frac{y}{x}$ $$frac{y^2}{x^2} = 2ln|x|+C.$$ Так как достаточно по условию задания найти общий интеграл дифференциального уравнения, то запишем ответ в виде $$frac{y^2}{x^2} — 2ln|x| = C.$$ |
| Ответ |
| $$frac{y^2}{x^2} — 2ln|x| = C$$ |
Начальные
условия
,
будучи набором из
чисел, задают точку пространства
.
Множество всех рассматриваемых вариантов
начальных условий образует некоторую
область
.
Для
различных видов ограничений на функцию
и на область
имеет место существование и единственность
решения задачи Коши для начальных
условий из
.
Приведем примеры соответствующих
теорем.
I.
Пусть уравнение 1-го порядка является
разрешённым относительно производной
:
.
Теорема 1. Если
функция
и ее частная производная
непрерывны в области
плоскости
,
то решение задачи Коши для любых начальных
условий
существует и единственно в некоторой
окрестности точки
.
II.
Пусть
уравнение
-го
порядка является разрешённым относительно
старшей производной
:
.
Теорема 2. Если
функция
и ее частные производные
непрерывны в области
-мерного
пространства
,
то решение задачи Коши для любых начальных
условий
существует и единственно в некоторой
окрестности точки
.
В дальнейшем будем
предполагать, что дифференциальные
уравнения рассматриваются в области
существования и единственности решения.
Определение.
Общим решением
дифференциального уравнения
-го
порядка называется функция
,
зависящая от аргумента
и от
произвольных постоянных
,
которая удовлетворяет двум условиям:
1) при любых значениях
произвольных постоянных эта функция
является решением;
2) за счет выбора
значений произвольных постоянных можно
получить решение задачи Коши для любых
начальных условий из области существования
и единственности решения.
Заметим, что
количество
произвольных постоянных равно порядку
уравнения.
Определение.
Частным
решением
дифференциального уравнения называется
функция, которая получается из общего
решения, если произвольным постоянным
придать определенные значения.
Напомним определение
неявной функции: функция
в окрестности
точки
,
задана неявно
уравнением
,
если при всех
из этой окрестности справедливо равенство
.
Обычное, «явное»
задание функции можно рассматривать
как частный случай неявного:
;
здесь
.
Определение.
Общим
интегралом
дифференциального уравнения
-го
порядка называется уравнение
,
(3)
зависящее от
произвольных постоянных
,
которое задает общее решение
как неявную функцию.
Определение.
Частным
интегралом
называется уравнение, которое получается
из общего интеграла (3), если произвольным
постоянным придать определенные
значения.
Замечание.
В тех случаях, когда удается найти
решение дифференциального уравнения,
оно имеет, как правило, вид общего
интеграла (3). Если при этом можно
явно выразить через
(«разрешить уравнение относительно
»),
то приходим к общему решению.
4. Метод разделения переменных
Определение.
Уравнением
с разделенными переменными называется
дифференциальное
уравнение первого порядка вида
,
(4)
с
непрерывными функциями
и
Смысл
этого термина заключается в том, что
переменные
и
разделены по разным частям равенства
(4).
Напомним,
что, согласно определению, дифференциал
функции
есть произведение производной на
дифференциал независимой переменной:
.
Если умножить обе части равенства (4) на
,
получим:
.
(5)
Это
другой, более традиционный способ записи
уравнения с разделенными переменными.
Теорема.
Если в уравнении (5) функции
и
имеют первообразные
и
,
то общий интеграл уравнения имеет вид:
,
(6)
где
—
произвольная постоянная.
Замечание.
Если для обозначения первообразных
использовать символ неопределенного
интеграла, то общий интеграл записывается
в виде:
.
(7)
Доказательство.
Опуская доказательство того, что
уравнение (6) действительно задает
неявную функцию
,
убедимся, что
удовлетворяет уравнению (4). Для этого
продифференцируем по
равенство (6), применяя для левой части
правило производной сложной функции с
промежуточной переменной
:
,
или,
учитывая, что
и
первообразные для
и
:
.
Остается
убедиться, что за счет выбора значения
произвольной постоянной
можно обеспечить выполнение любых
начальных условий
.
Подставляя начальные условия в (6),
получаем:
.
▄
Примеры.
1. Для уравнения
найдем общий интеграл и частный интеграл
для начальных условий
.
Имеем:
—
это
общий интеграл.
Подставим
теперь в общий интеграл начальные
условия и найдем соответствующее
значение константы
:
.
Следовательно,
частный интеграл, дающий решение задачи
Коши, имеет вид:
.
2.
Рассмотрим уравнение
с начальными условиями
.
Умножая обе части уравнения на
и затем интегрируя, получаем:
– это
общий интеграл. Выражая отсюда явно
через
и
,
получаем общее решение:
.
Подстановка начальных условий в общее
решение дает:
,
так что
.
Следовательно, функция
является решением задачи Коши.
Определение.
Уравнением
с разделяющимися переменными называется
дифференциальное
уравнение первого порядка вида
,
(8)
с
непрерывными функциями
.
В
этом уравнении каждая из частей является
произведением двух множителей, один из
которых зависит только от
,
а другой – только от
.
От
этого уравнения легко перейти к уравнению
с разделенными переменными, деля обе
части на произведение
(«разделяя переменные»):
.
Примеры.
1.
.
Обе части разделим на
и умножим на
:
.
Интегрируем:
—
общий
интеграл.
2.
;
начальные условия:
.
Записываем производную
как отношение дифференциалов:
.
Обе
части умножим на
,
разделим на
и проинтегрируем:
—
общий
интеграл. Найдем теперь частный интеграл,
удовлетворяющий начальным условиям.
Подставляя начальные условия в полученное
уравнение, имеем:
;
.
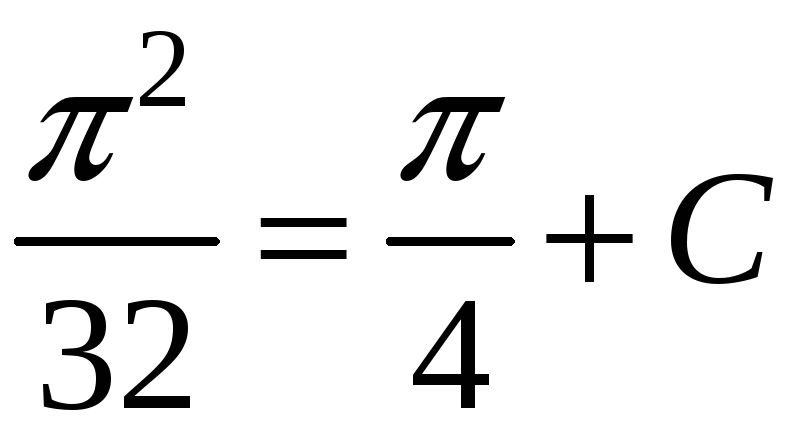
Следовательно,
частный интеграл, дающий решение задачи
Коши, имеет вид:
.
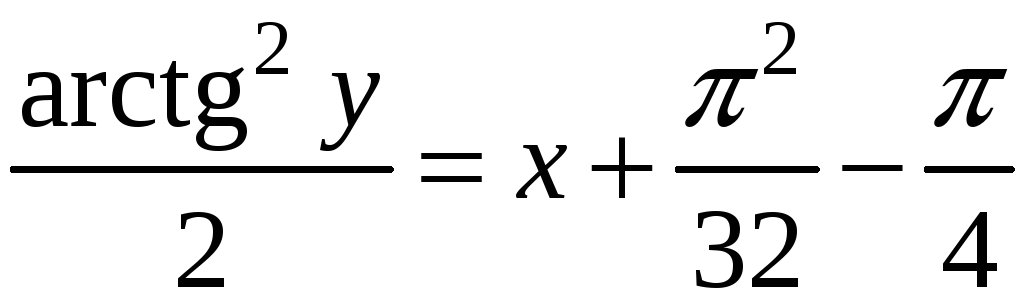
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Примеры дифференциальных уравнений с решениями
- Попробуйте решить приведенные ниже дифференциальные уравнения.
- Нажмите на изображение уравнения, и вы попадете на страницу с подробным решением.
Примеры решений дифференциальных уравнений первого порядка
Примеры решений дифференциальных уравнений второго и высших порядков
Найти общее решение дифференциального уравнения, или решение с заданными начальными условиями.
Примеры решений линейных дифференциальных уравнений с постоянными коэффициентами
Примеры решений линейных уравнений в частных производных первого порядка
Найти общее решение линейного однородного уравнения в частных производных первого порядка и решить задачу Коши с указанным граничным условием:
,
при .
Найти поверхность, удовлетворяющую данному уравнению
,
и проходящую через данную окружность
, .
Автор: Олег Одинцов . Опубликовано: 28-01-2016 Изменено: 26-11-2021
Примеры решения дифференциальных уравнений с ответами
Простое объяснение принципов решения дифференциальных уравнений и 10 наглядных примеров. В каждом примере поэтапный ход решения и ответ.
Алгоритм решения дифференциальных уравнений
Дифференциальные уравнения не так сильно отличаются от привычных уравнений, где необходимо найти переменную x , как кажется на первый взгляд. Всё различие лишь в том, что в дифференциальных уравнениях мы ищем не переменную, а функцию у(х) , с помощью которой можно обратить уравнение в равенство.
Дифференциальное уравнение – это уравнение, содержащее саму функцию (y=y(x)), производные функции или дифференциалы (y′, y″) и независимые переменные (наиболее распространённая – х). Обыкновенным дифференциальным уравнением называют уравнение, в котором содержится неизвестная функция под знаком производной или под знаком дифференциала.
Чтобы решить ДУ, необходимо найти множество всех функций, которые удовлетворяют данному уравнению. Это множество в большинстве случаев выглядит следующим образом:y=f(x; С), где С – произвольная постоянная.
Проверить решённое ДУ можно, подставив найденную функцию в изначальное уравнение и убедившись, что уравнение обращается в тождество (равенство).
Примеры решения дифференциальных уравнений
Задание
Решить дифференциальное уравнение xy’=y.
Решение
В первую очередь, необходимо переписать уравнение в другой вид. Пользуясь
переписываем дифференциальное уравнение, получаем
Дальше смотрим, насколько реально разделить переменные, то есть путем обычных манипуляций (перенос слагаемых из части в часть, вынесение за скобки и пр.) получить выражение, где «иксы» с одной стороны, а «игреки» с другой. В данном уравнении разделить переменные вполне реально, и после переноса множителей по правилу пропорции получаем
Далее интегрируем полученное уравнение:
В данном случае интегралы берём из таблицы:
После того, как взяты интегралы, дифференциальное уравнение считается решённым. Решение дифференциального уравнения в неявном виде называется общим интегралом дифференциального уравнения.
– это общий интеграл. Также для удобства и красоты, его можно переписать в другом виде: y=Cx, где С=Const
Ответ
Задание
Найти частное решение дифференциального уравнения
Решение
Действуем по тому же алгоритму, что и в предыдущем решении.
Переписываем производную в нужном виде, разделяем переменные и интегрируем полученное уравнение:
Получили общий интеграл.Далее, воспользуемся свойством степеней, выразим у в «общем» виде и перепишем функцию:
Если – это константа, то
0]» title=»Rendered by QuickLaTeX.com» />
– тоже некоторая константа, заменим её буквой С:
– убираем модуль и теперь константа может принимать и положительные, и отрицательные значения.
Получаем общее решение:
Ответ
Задание
Решить дифференциальное уравнение
Решение
В первую очередь необходимо переписать производную в необходимом виде:
Второй шаг – разделение переменных и перенос со сменой знака второго слагаемого в правую часть:
После разделения переменных, интегрируем уравнение, как в примерах выше.
Чтобы решить интегралы из левой части, применим метод подведения функции под знак дифференциала:
В ответе мы получили одни логарифмы и константу, их тоже определяем под логарифм.
Далее упрощаем общий интеграл:
Приводим полученный общий интеграл к виду: F(x,y)=C:
Чтобы ответ смотрелся красивее, обе части необходимо возвести в квадрат.
Ответ
Задание
Найти частное решение дифференциального уравнения
удовлетворяющее начальному условию y(0)=ln2.
Решение
Первый шаг – нахождение общего решения. То, что в исходном уравнении уже находятся готовые дифференциалы dy и dx значительно упрощает нам решение.
Начинаем разделять переменные и интегрировать уравнение:
Мы получили общий интеграл и следующий шаг – выразить общее решение. Для этого необходимо прологарифмировать обе части. Знак модуля не ставим, т.к. обе части уравнения положительные.
Получаем общее решение:
Далее необходимо найти частное решение, которое соответствует заданному начальному условию y(0)=ln2.
В общее решение вместо «икса» подставляем ноль, а вместо «игрека» логарифм двух:
Подставляем найденное значение константы C=1 в общее решение.
Ответ
Задание
Решить дифференциальное уравнение
Решение
При внимательном разборе данного уравнения видно, что можно разделить переменные, что и делаем, после интегрируем:
В данном случае константу C считается не обязательным определять под логарифм.
Ответ
Задание
Найти частное решение дифференциального уравнения
удовлетворяющее начальному условию y(1)=e. Выполнить проверку.
Решение
Как и в предыдущих примерах первым шагом будет нахождение общего решения. Для этого начинаем разделять переменные:
Общий интеграл получен, осталось упростить его. Упаковываем логарифмы и избавляемся от них:
можно выразить функцию в явном виде.
Осталось найти частное решение, удовлетворяющее начальному условию y(1)=e.
Подставляем найденное значение константы C=1 в общее решение.
Ответ
Проверка
Необходимо проверить, выполняется ли начальное условие:
Из равенства выше видно, что начальное условие y(1)=e выполнено.
Далее проводим следующую проверку: удовлетворяет ли вообще частное решение
дифференциальному уравнению. Для этого находим производную:
Подставим полученное частное решение
и найденную производную в исходное уравнение
Получено верное равенство, значит, решение найдено правильно.
Задание
Найти общий интеграл уравнения
Решение
Данное уравнение допускает разделение переменных. Разделяем переменные и интегрируем:
Ответ
Задание
Найти частное решение ДУ.
Решение
Данное ДУ допускает разделение переменных. Разделяем переменные:
Найдем частное решение (частный интеграл), соответствующий заданному начальному условию
Подставляем в общее решение
Ответ
Задание
Решить дифференциальное уравнение
Решение
Данное уравнение допускает разделение переменных. Разделяем переменные и интегрируем:
Левую часть интегрируем по частям:
В интеграле правой части проведем замену:
(здесь дробь раскладывается методом неопределенных коэффициентов)
Ответ
Задание
Решить дифференциальное уравнение
Решение
Данное уравнение допускает разделение переменных.
Разделяем переменные и интегрируем:
Методом неопределенных коэффициентов разложим подынтегральную функцию в сумму элементарных дробей:
Как найти общий интеграл уравнения примеры
1. У равнения с разделяющимися переменными
Общий вид уравнений
С учетом равенства
уравнение (8.10) может быть записано в виде .
Разделим обе части на произведение функций M ( x )∙ Q ( y ) (при условии ) и после сокращения получим: . Так как переменные разделены, проин тегрируем уравнение почленно: . После нахождения интегралов получаем общий интеграл исходного ДУ. Предполагая, что , мы могли потерять решения. Следовательно, необходимо подстановкой M ( x )=0, Q ( y )=0 в исходное уравнение сделать проверку. В том случае, когда данные функции удовлетворяют уравнению, они также являются его решениями.
Пример 8.2. Проинтегрировать уравнение .
Решение . Представим уравнение в виде . Разделим переменные: . Проинтегрируем уравнение:
После применения теоремы о сумме логарифмов и потенцирования получаем
2. Однородные дифференциальные уравнения первого порядка
Общий вид уравнений
где M ( x ; y ) и N ( x ; y )– однородные функции аргументов x и y одного и того же измерения m , то есть имеют место равенства
Метод решения уравнения (8.12) – деление на переменную x в степени измерения m : . Далее уравнение преобразуются с помощью следующей замены:
Однородное уравнение (8.12) принимает вид: – уравнение с разделяющимися переменными. Следовательно, дальнейшее решение – по пункту 1.
Пример 8.3. Проинтегрировать уравнение .
Решение. Поделим уравнение на x 2 , получим . После замены (8.14) заданное по условию уравнение принимает вид , . В результате интегрирования получим . После обратной замены – искомый общий интеграл
Пример 8.4. Найти общее решение (общий интеграл) дифференциального уравнения .
Решение . Правая часть уравнения обладает свойством . Поэтому заданное уравнение является однородным дифференциальным уравнением первого порядка. Совершим замену , где u – некоторая функция от аргумента x . Отсюда . Исходное уравнение приобретает вид
или . Разделим переменные: .
После интегрирования обеих частей уравнения получаем
Потенцируя, находим .
Итак, общий интеграл исходного уравнения приобретает вид cy = x 2 + y 2 , где c – произвольная постоянная
3. Дифференциальные уравнения первого порядка, приводящиеся к однородным или к уравнениям с разделяющимися переменными
Общий вид уравнений
где – числа.
При c 1 = c 2 = 0 уравнение является однородным. Рассмотрим два случая при c 1 и c 2 не равных нулю одновременно.
1) Определитель . Вводят новые переменные u и v , положив x = u + x 0 , y = v + y 0 , где ( x 0 ; y 0 ) – решение системы уравнений .
В результате данной подстановки уравнение (8.15) становится однородным.
Пример 8.5. Найти общее решение (общий интеграл) дифференциального уравнения .
Решение . Определитель , следовательно, решаем систему уравнений . Получаем значения x 0 = – 1; y 0 =2, с использованием которых осуществляем замену x = u – 1; y = v + 2, при этом . Заданное по условию ДУ принимает вид:
, (*) – однородное ДУ относительно функции v и переменной u .
С помощью формул интегрирования (4.8) и (4.17) получаем:
Осуществим обратную подстановку :
– общий интеграл исходного уравнения
2) Определитель . Это означает пропорциональность коэффициентов или
Пример 8.6. Найти общее решение (общий интеграл) дифференциального уравнения
Решение . Определитель , следовательно, осуществляем замену
Исходное уравнение принимает вид:
Далее . Разделим переменные: или . Проинтегрируем уравнение:
После обратной замены получим: – общий интеграл исходного уравнения
4. Линейные дифференциальные уравнения первого порядка
Общий вид уравнений
где P ( x ) и Q ( x ) – заданные функции (могут быть постоянными).
Уравнение (8.16) может быть решено двумя способами.
1) Метод Бернулли-Фурье состоит в том, что решение ищется в виде произведения двух неизвестных функций y ( x )= u ( x )∙ v ( x ) или коротко y = u ∙ v , при этом . Одна из функций будет представлять общую часть решения и содержать константу интегрирования c , другая функция может быть взята в частном виде при конкретном значении константы (общее решение ДУ первого порядка должно содержать одну константу интегрирования). Подставим выражения y и в (8.16), после чего оно принимает вид:
Функцию v ( x ) подберем в частном виде так, чтобы выражение в скобках обратилось в ноль. Для этого решим уравнение с разделяющимися переменными или . Отсюда в результате интегрирования получим: . Так функция v ( x ) выбиралась произвольно, то можно положить c = 1, тогда . Подставив найденную v ( x ) в (8.17), приходим к еще одному уравнению с разделяющимися переменными . Интегрируя его, получим функцию . Общее решение исходного ДУ (8.16) принимает вид
Пример 8.7. Проинтегрировать уравнен ие с помощью метода Бернулли.
Решение . Данное уравнение является линейным ДУ первого порядка с функциями . Применим подстановку y = u ∙ v , где u и v – некоторые функции аргумента x . Так как y = u ∙ v , то , и заданное уравнение принимает вид:
Выберем функцию u так, чтобы выражение, стоящее в скобках, обращалось в ноль, то есть и л и
Полагая c = 1, получим u = cos x . При таком выборе функции u уравнение (**) примет вид:
. Отсюда v=tg x+c . Тогда – общее решение заданного уравнения.
Общее решение заданного ДУ можно также получить, пользуясь непосредственно формулой (8.18):
По условию задачи имеем: P ( x )= tg x , . Следовательно, . Так как , то с использованием основного логарифмического тождества получаем:
Таким образом, – общее решение исходного дифференциального уравнения
2) Метод Лагранжа иначе называют методом вариации произвольной постоянной. Рассмотрим сначала соответствующее линейное однородное ДУ первого порядка, то есть исходное уравнение без правой части . Разделив переменные и проинтегрировав, в найденном решении полагают постоянную c функцией c ( x ). После этого функцию y дифференцируют и вместе с подставляют в исходное уравнение. При этом получают уравнение относительно неизвестной функции c ( x ), отыскав которую, подставляют ее в y – общее решение заданного линейного неоднородного уравнения (с правой частью).
Пример 8.8. Проинтегрировать уравнение с помощью метода Лагранжа (сравни с пример ом 8.7).
Решение . Решим сначала соответствующее линейное однородное ДУ первого порядка или . Разделим переменные: . В результате интегрирования получаем: – общее решение соответствующего однородного уравнения. Применим метод варьирования константы, то есть предположим c = c ( x ). Тогда общее решение исходного линейного неоднородного уравнения будет иметь вид: . Подставим y и в исходное уравнение:
Подставляя найденное c ( x ) в y , имеем общее решение линейного неоднородного уравнения:
5. Уравнения Бернулли
Общий вид уравнений
При n = 1 (8.1 9) – уравнение с разделяющимися переменными. При n = 0 (8.1 9) – линейное ДУ.
Рассмотрим . Метод решения – деление уравнения на , после чего (8.1 9) принимает вид . С помощью замены z = y – n +1 исходное уравнение становится линейным относительно функции z ( x ):
то есть его решение находится аналогично пункту 4. На практике искать решение уравнения (8.17) удобнее методом Бернулли в виде произведения неизвестных функций y = u ∙ v . Заметим, что y = 0 – всегда является решением исходного уравнения (8.17).
Пример 8.9. Проинтегрировать уравнение .
Решение. Заданное уравнение является уравнением Бернулли. Положим y = u ∙ v , тогда и уравнение примет вид:
Выберем функцию u так, чтобы выполнялось равенство: . Разделим переменные и проинтегрируем:
Тогда заданное уравнение после сокращения на u примет вид: или – уравнение с разделяющимися переменными. Находим его общее решение: . Интегрируя последнее уравнение, получим: . Следовательно, общее решение заданного уравнения имеет вид:
6. Уравнения в полных дифференциалах
6.1. Общий вид уравнений
где левая часть есть полный дифференциал некоторой функции F ( x ; y ), то есть . В этом случае ДУ (8.21) можно записать в виде , а его общий интеграл будет F ( x ; y )= c .
Условие, по которому можно судить, что выражение является полным дифференциалом, можно сформулировать в виде следующей теоремы.
Теорема 8.2. Для того чтобы выражение , где функции M ( x ; y ) и N ( x ; y ), их частные производные и непрерывны в некоторой области D плоскости x 0 y , было полным дифференциалом, необходимо и достаточно выполнение условия
(8.22)
Таким образом, согласно определению полного дифференциала (6.6) должны выполняться равенства:
Формула (8.22) представляет собой теорему Шварца, согласно которой смешанные производные второго порядка функции F ( x ; y ) равны.
Зафиксируем переменную y и проинтегрируем первое уравнение из (8.23) по x , получим:
Здесь мы применили метод вариации произвольной постоянной, так как предположили, что константа c зависит от y (либо является числом). Продифференцировав (8.24) по переменной y и приравняв производную к функции N ( x ; y ), мы получим уравнение для нахождения неизвестной c ( y ). Подставив c ( y ) в (8.24), находим функцию F ( x ; y ) такую, что .
Пример 8.10. Решить уравнение .
Решение. Здесь функция .
Проверим условие (8.22): . Следовательно, левая часть заданного уравнения представляет собой полный дифференциал некоторой функции F ( x ; y ). Для ее отыскания проинтегрируем функцию M ( x ; y ) по переменной x , считая y = const :
Пусть c = c ( y ), тогда . Продифференцируем данную функцию по y , получим . Отсюда .
Найденное c ( y ) подставляем в функцию F ( x ; y ), получаем решение заданного ДУ:
Если условие (8.22) не выполняется, то ДУ (8.21) не является уравнением в полных дифференциалах.
Однако это уравнение иногда можно привести к уравнению в полных дифференциалах умножением его на некоторую функцию μ ( x ; y ), называемую интегрирующим множителем .
Чтобы уравнение было уравнение в полных дифференциалах, должно выполняться условие
Выполнив дифференцирование и приведя подобные слагаемые, получим: . Для нахождения μ ( x ; y ) надо проинтегрировать полученное ДУ в частных производных. Решение этой задачи не простое. Нахождение интегрирующего множителя может быть упрощено, если допустить существование μ как функции только одного аргумента x либо только y .
6.2. Пусть μ = μ ( x ). Тогда уравнение (8.25) принимает вид:
При этом подынтегральное выражение должно зависеть только от x.
6.3. Пусть μ = μ ( y ). Тогда аналогично можно получить
где подынтегральное выражение должно зависеть только от y .
Пример 8.11. Решить уравнение .
Решение . Здесь , то есть . Проверим существование интегрирующего множителя. По формуле (8.26) составляем подынтегральное выражение:
7. Дифференциальные уравнения, не разрешенные относительно производной
К уравнениям данного вида относятся уравнения Лагранжа и Клеро, которые образуют достаточно большой класс ДУ, решаемых методом введения параметра .
7.1. Уравнение Лагранжа
Общий вид уравнений
где φ и ψ– известные функции от . После введения параметра уравнение (8.28) принимает вид
Продифференцируем его по x :
Полученное уравнение (8.30) является линейным уравнением относительно неизвестной функции x = x ( p ). Решив его, найдем:
Исключая параметр p из уравнений (8.29) и (8.31), получаем общий интеграл уравнения (8.28) в виде y = γ ( x ; c ).
Примечание. При переходе к уравнению (8.30) мы делили на . При этом могли быть потеряны решения, для которых или p = p 0 = const . Это означает, что p 0 является корнем уравнения p = φ ( p )=0 (смотри уравнение (8.30)). Тогда решение для уравнения (8.28) является особым
7.2. Уравнение Клеро представляет собой частный случай уравнения Лагранжа при , следовательно, его общий вид
. (8.32)
Вводим параметр , после чего уравнение (8.30) записывается так:
Продифференцируем уравнение (8.33) по переменной x:
При получаем частное решение уравнения в параметрической форме:
Это – особое решение уравнения Клеро, так как оно не содержится в формуле общего решения уравнения.
Пример 8.12. Решить уравнение Клеро .
Решение. Согласно формуле (8.32) общее решение имеет вид y = cx + c 2 . Особое решение уравнения получим по (8.33) в виде . Отсюда следует: , то есть
http://nauchniestati.ru/spravka/primery-resheniya-differenczialnyh-uravnenij-s-otvetami/
http://www.sites.google.com/site/vyssaamatem/glava-viii-elementy-teorii-obyknovennyh-differencialnyh-uravnenij/viii-2-nekotorye-vidy-differencialnyh-uravnenij-pervogo-poradka