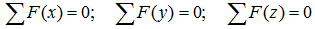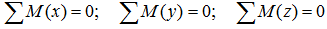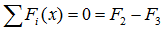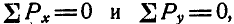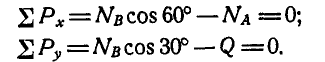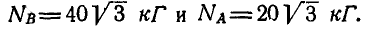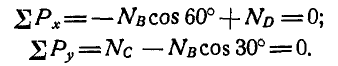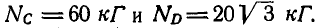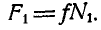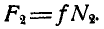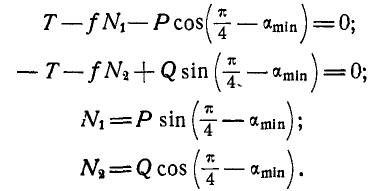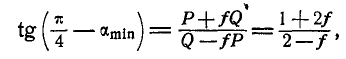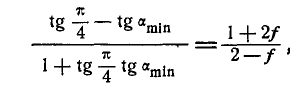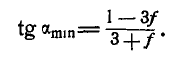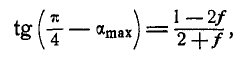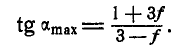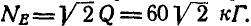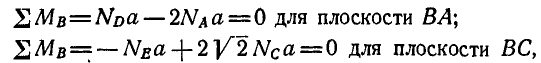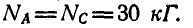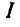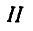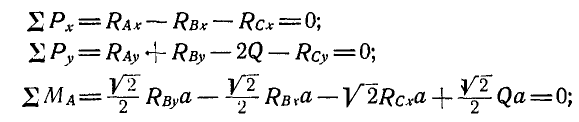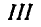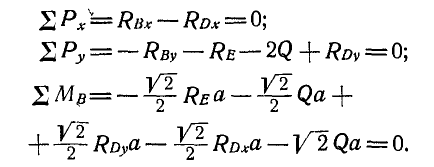Материалы из методички: Сборник задач по теоретическим основам химии для студентов заочно-дистанционного отделения / Барботина Н.Н., К.К. Власенко, Щербаков В.В. – М.: РХТУ им. Д.И. Менделеева, 2007. -155 с.
Понятие химического равновесия
Признаки химического равновесия
Принцип Ле Шателье
Влияние температуры на химическое равновесие
Влияние давления на химическое равновесие
Влияние концентрации на химическое равновесие
Константа химического равновесия
Примеры решения задач
Задачи для самостоятельного решения
Понятие химического равновесия
Равновесным считается состояние системы, которое остается неизменным, причем это состояние не обусловлено действием каких-либо внешних сил. Состояние системы реагирующих веществ, при котором скорость прямой реакции становится равной скорости обратной реакции, называется химическим равновесием. Такое равновесие называется еще подвижным или динамическим равновесием.
Признаки химического равновесия
- Состояние системы остается неизменным во времени при сохранении внешних условий.
- Равновесие является динамическим, то есть обусловлено протеканием прямой и обратной реакции с одинаковыми скоростями.
- Любое внешнее воздействие вызывает изменение в равновесии системы; если внешнее воздействие снимается, то система снова возвращается в исходное состояние.
- К состоянию равновесия можно подойти с двух сторон – как со стороны исходных веществ, так и со стороны продуктов реакции.
- В состоянии равновесия энергия Гиббса достигает своего минимального значения.
Принцип Ле Шателье
Влияние изменения внешних условий на положение равновесия определяется принципом Ле Шателье (принципом подвижного равновесия):
Если на систему, находящуюся в состоянии равновесия, производить какое–либо внешнее воздействие, то в системе усилится то из направлений процесса, которое ослабляет эффект этого воздействия, и положение равновесия сместится в том же направлении.
Принцип Ле Шателье применим не только к химическим процессам, но и к физическим, таким как кипение, кристаллизация, растворение и т. д.
Рассмотрим влияние различных факторов на химическое равновесие на примере реакции окисления NO:
2NO(г) + O2(г) → 2NO2(г); ΔHо298 = — 113,4 кДж/моль.
Влияние температуры на химическое равновесие
При повышении температуры равновесие сдвигается в сторону эндотермической реакции, при понижении температуры – в сторону экзотермической реакции.
Степень смещения равновесия определяется абсолютной величиной теплового эффекта: чем больше по абсолютной величине энтальпия реакции ΔH, тем значительнее влияние температуры на состояние равновесия.
В рассматриваемой реакции синтеза оксида азота (IV) повышение температуры сместит равновесие в сторону исходных веществ.
Влияние давления на химическое равновесие
Сжатие смещает равновесие в направлении процесса, который сопровождается уменьшением объема газообразных веществ, а понижение давления сдвигает равновесие в противоположную сторону.
В рассматриваемом примере в левой части уравнения находится три объема, а в правой – два. Так как увеличение давления благоприятствует процессу, протекающему с уменьшением объема, то при повышении давления равновесие сместится вправо, т.е. в сторону продукта реакции – NO2. Уменьшение давления сместит равновесие в обратную сторону. Следует обратить внимание на то, что, если в уравнении обратимой реакции число молекул газообразных веществ в правой и левой частях равны, то изменение давления не оказывает влияния на положение равновесия.
Влияние концентрации на химическое равновесие
Для рассматриваемой реакции введение в равновесную систему дополнительных количеств NO или O2 вызывает смещение равновесия в том направлении, при котором концентрация этих веществ уменьшается, следовательно, происходит сдвиг равновесия в сторону образования NO2. Увеличение концентрации NO2 смещает равновесие в сторону исходных веществ.
Катализатор одинаково ускоряет как прямую, так и обратную реакции и поэтому не влияет на смещение химического равновесия.
При введении в равновесную систему (при Р = const) инертного газа концентрации реагентов (парциальные давления) уменьшаются. Поскольку рассматриваемый процесс окисления NO идет с уменьшением объема, то при добавлении инертного газа равновесие сместится в сторону исходных веществ.
Константа химического равновесия
Для химической реакции:
2NO(г) + O2(г) → 2NO2(г)
константа химической реакции Кс есть отношение:
Кс = [NO2]2/([NO]2 · [O2]) (1)
В этом уравнении в квадратных скобках – концентрации реагирующих веществ, которые устанавливаются при химическом равновесии, т.е. равновесные концентрации веществ.
Константа химического равновесия связана с изменением энергии Гиббса уравнением:
ΔGTо = – RTlnK (2)
Примеры решения задач
Задача 1. При некоторой температуре равновесные концентрации в системе 2CO (г) + O2 (г)→2CO2 (г) составляли: [CO] = 0,2 моль/л, [O2] = 0,32 моль/л, [CO2] = 0,16 моль/л. Определите константу равновесия при этой температуре и исходные концентрации CO и O2, если исходная смесь не содержала СО2.
Решение.
2CO(г) + O2(г) →2CO2(г)
|
Вещество |
CO | O2 | CO2 |
| Сисходн, моль/л | 0,36 | 0,40 | 0 |
| Спрореагир,моль/л | 0,16 | 0,08 | 0,16 |
| Сравн, моль/л | 0,2 | 0,32 | 0,16 |
Во второй строке под Спрореагир понимается концентрация прореагировавших исходных веществ и концентрация образующегося CO2, причем, Сисходн= Спрореагир + Сравн.
Задача 2. Используя справочные данные, рассчитайте константу равновесия процесса
3 H2 (г) + N2 (г) →2 NH3 (г) при 298 К.
Решение.
ΔG298о = 2·(- 16,71) кДж = -33,42·103 Дж.
ΔGTо = — RTlnK.
lnK = 33,42·103/(8,314× 298) = 13,489. K = 7,21× 105.
Задача 3. Определите равновесную концентрацию HI в системе
H2(г) + I2(г) →2HI(г),
если при некоторой температуре константа равновесия равна 4, а исходные концентрации H2 , I2 и HI равны, соответственно, 1, 2 и 0 моль/л.
Решение. Пусть к некоторому моменту времени прореагировало x моль/л H2.
| Вещество | H2 | I2 | HI |
| сисходн., моль/л | 1 | 2 | 0 |
| спрореагир., моль/л | x | x | 2x |
| cравн., моль/л | 1-x | 2-x | 2x |
Тогда, К = (2х)2/((1-х)(2-х))
Решая это уравнение, получаем x = 0,67.
Значит, равновесная концентрация HI равна 2× 0,67 = 1,34 моль/л.
Задача 4. Используя справочные данные, определите температуру, при которой константа равновесия процесса: H2(г) + HCOH(г) →CH3OH(г) становится равной 1. Принять, что ΔНоТ » ΔНо298, а ΔSоT » ΔSо298.
Решение.
Если К = 1, то ΔGоT = — RTlnK = 0;
ΔGоT = ΔНо298 — ТΔ Sо298 .
ΔНо298 = -202 – (- 115,9) = -86,1 кДж = — 86,1× 103 Дж;
ΔSо298 = 239,7 – 218,7 – 130,52 = -109,52 Дж/К;
0 = — 86100 — Т·(-109,52)
Т = 786,15К
Задача 5. Для реакции SO2(Г) + Cl2(Г) →SO2Cl2(Г) при некоторой температуре константа равновесия равна 4. Определите равновесную концентрацию SO2Cl2, если исходные концентрации SO2, Cl2 и SO2Cl2 равны 2, 2 и 1 моль/л соответственно.
Решение. Пусть к некоторому моменту времени прореагировало x моль/л SO2.
SO2(г) + Cl2(г) →SO2Cl2(г)
| Вещество | SO2 | Cl2 | SO2Cl2 |
| cисходн., моль/л | 2 | 2 | 1 |
| cпрореагир., моль/л | x | x | х |
| cравн., моль/л | 2-x | 2-x | x + 1 |
Тогда получаем:
(х + 1)/(2 — х)2 = 4
Решая это уравнение, находим: x1 = 3 и x2 = 1,25. Но x1 = 3 не удовлетворяет условию задачи.
Следовательно, [SO2Cl2] = 1,25 + 1 = 2,25 моль/л.
Задачи для самостоятельного решения
1. В какой из приведенных реакций повышение давления сместит равновесие вправо? Ответ обоснуйте.
1) 2 NH3 (г) → 3H2 (г) + N2 (г)
2) ZnCO3 (к) → ZnO(к) + CO2 (г)
3) 2HBr (г) → H2 (г) + Br2 (ж)
4) CO2 (г) + C (графит) →2CO (г)
|
Так как увеличение давления благоприятствует процессу, протекающему с уменьшением количества |
2. При некоторой температуре равновесные концентрации в системе:
2HBr (г) →H2 (г) + Br2 (г)
составляли: [HBr] = 0,3 моль/л, [H2] = 0,6 моль/л, [Br2] = 0,6 моль/л. Определите константу равновесия и исходную концентрацию HBr.
3. Для реакции H2(г) + S(г) →H2S(г) при некоторой температуре константа равновесия равна 2. Определите равновесные концентрации H2 и S, если исходные концентрации H2, S и H2S равны, соответственно, 2, 3 и 0 моль/л.
4. Используя справочные данные, вычислите температуру, при которой константа равновесия процесса
CO2(г) + C(графит) →2CO(г)
становится равной 1. Примите, что ΔНоТ≈ΔНо298, а ΔSоT≈ΔSо298
5. Используя справочные данные, рассчитайте константу равновесия процесса:
С2Н4(г) →С2Н2(г) + Н2(г) при 298 К
6. Для реакции 2С3Н8(г) → н-С5Н12(г)+СН4(г) при температуре 1000 К константа равновесия равна 4. Определите равновесную концентрацию н-пентана, если исходная концентрация пропана равна 5 моль/л.
7. При температуре 500 К константа равновесия процесса:
СО2(г) + 3Н2(г) → СН3ОН(г) + Н2О(г)
равна 3,4·10-5. Вычислите Δ Gо500.
8. При температуре 800 К константа равновесия процесса н-С6Н14(г)+ 2С3Н6(г)+Н2(г) равна 8,71. Определите ΔGоf,800(С3Н6(г)), если ΔGоf,800(н-С6Н14(г)) = 305,77 кДж/моль.
9. Для реакции СО(г) + Cl2(г) →СO2Cl2(г) при некоторой температуре равновесная концентрация СO2Cl2(г) равна 1,2 моль/л. Определите константу равновесия данного процесса, если исходные концентрации СО(г) и Cl2(г) равны соответственно 2,0 и 1,8 моль/л.
10. При некоторой температуре равновесные концентрации в системе 2SО2(г) + О2(г) →2SO3(г) составляли: [SО2 ]=0,10 моль/л, [О2]=0,16 моль/л, [SО3]=0,08 моль/л. Вычислите константу равновесия и исходные концентрации SО2 и О2.
|
К=4,0; исходная концентрация SО2 составляет 0,18 моль/л; |
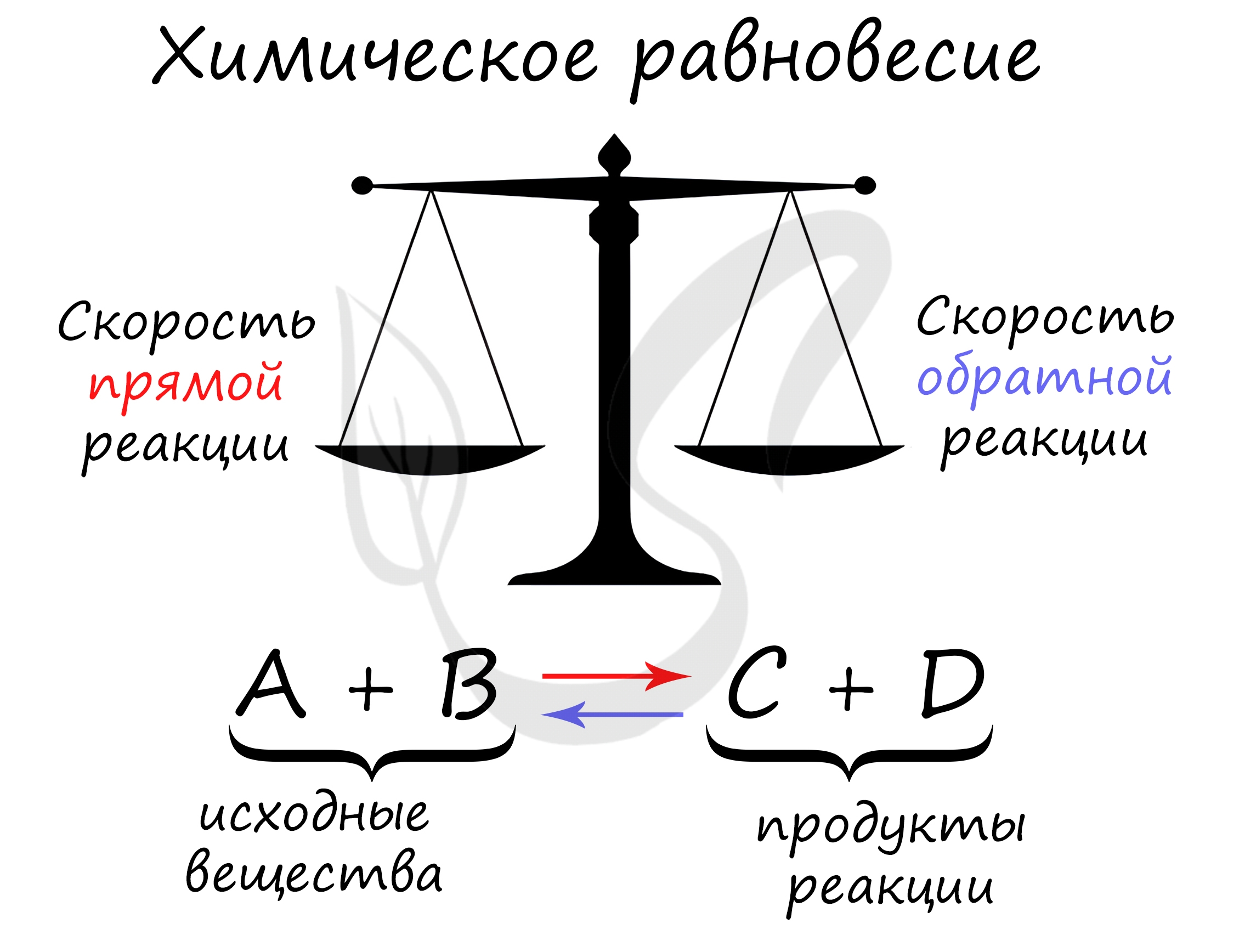
Химическое равновесие — состояние химической системы, при котором скорость прямой реакции равна скорости обратной.
В большом количестве заданий, которые мне довелось увидеть, я ни один раз видел, как коверкают это определение. Например, в заданиях верно-неверно
предлагают похожий вариант, однако говорят о «равенстве концентраций исходных веществ и продуктов» — это грубая ошибка. Химическое равновесие —
равенство скоростей.
Принцип Ле Шателье
В 1884 году французским химиком Анри Ле Шателье был предложен принцип, согласно которому, если на систему, находящуюся в состоянии
равновесия, оказать внешнее воздействие (изменить температуру, давление, концентрацию), то система будет стремиться компенсировать
внешнее воздействие.

Это принцип обоснован термодинамически и доказан. Однако в такой абстрактной формулировке его сложно применить для решения конкретных
задач по химическому равновесию. В этой статье я покажу конкретные примеры и обозначу алгоритм действия, чтобы вы могли успешно
справляться с заданиями.
Влияние изменения концентрации на химическое равновесие
При увеличении концентрации какого-либо компонента химической реакции, система будет стремиться восстановить равновесие:
равновесие будет смещаться в сторону расходования добавленного компонента.
Объясню проще: если вы увеличиваете концентрацию вещества, которое находится в левой части, равновесие сместится в правую сторону.
Если добавляете вещество из левой части (продуктов реакции) — смещается в сторону исходных веществ. Посмотрите на пример ниже.

Если мы попытаемся удалить какое-либо вещество из системы (уменьшить его концентрацию), то система будет стремиться заполнить «пустое»
место, которые мы создали. Наглядно демонстрирую на примере:
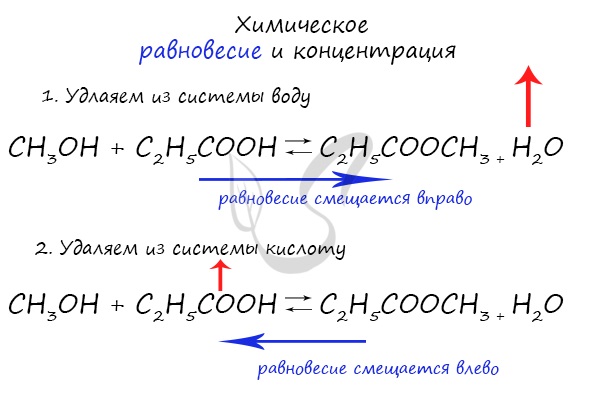
Можно подвести итог полученным знаниям таким образом: «Куда добавляем — оттуда смещается, откуда берем — туда смещается». Воспользуйтесь
этой или придумайте свое правило для запоминания этой закономерности 
Изменения давления и химическое равновесие
Если речь в задании идет об изменении давления, то первое, что нужно сделать, это посчитать количество газов в уравнении слева и справа.
Твердые вещества и жидкости считать не нужно. Например:
CO2(г) + С(тв) ⇄ 2CO(г) — Q
В приведенном уравнении количество молекул газа в левой части — 1, в правой — 2.
Запомните правило: «При увеличении давления равновесие смещается в сторону меньших газов, при уменьшении давления — в сторону больших газов».
Для нашей системы правило действует таким образом:

В случае, если слева и справа количество молекул газа одинаково, например, в реакции:
H2(г) + I2(г) ⇄ 2HI(г) — Q
Слева — 2 газа, и справа — 2. В такой реакции увеличение или уменьшение давления не повлияет на химическое равновесие.
Изменение температуры и химическое равновесие
Если в задании увеличивают или уменьшают температуру, то первое, что вы должны оценить: экзотермическая это реакция или
эндотермическая.
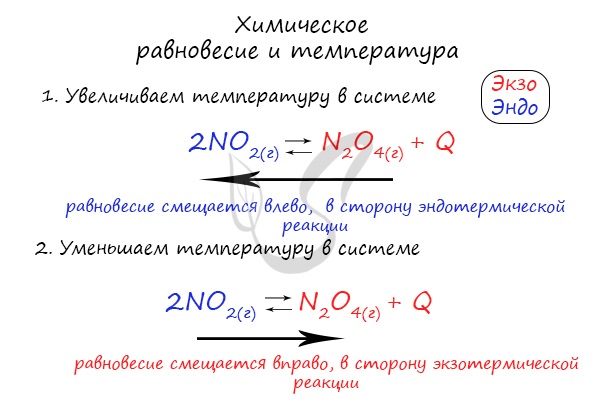
Следуйте следующему правилу: «При увеличении температуры равновесие смещается в сторону эндотермической реакции, при
уменьшении — в сторону экзотермической реакции». У любой обратимой реакции есть экзо- и эндотермические части:
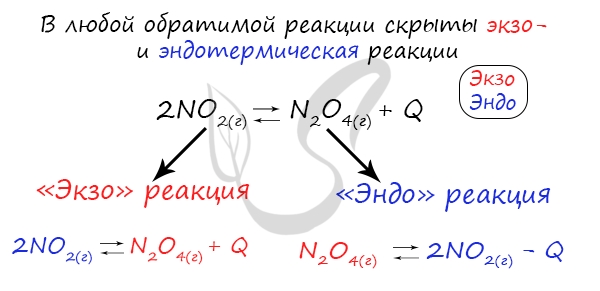
Поэтому данное правило универсально и применимо для всех реакций. Для примера разберем следующие задачи:

Чтобы не осталось белых пятен, возьмем экзотермическую реакцию и повторим с ней подобный эксперимент.
Катализатор и ингибитор
Действие катализатора и ингибитора соответственно касается только ускорения и замедления химической реакции. Они никоим образом не влияют на равновесие.
Константа равновесия
Константой равновесия называют отношения скоростей прямой и обратной реакции. Для реакции типа aA + bB = cC + dD константа
равновесия будет записана следующим образом:

Решим задачу. Дана реакция: 2NO + Cl2 ⇄ 2NOCl . Вычислите константу равновесия, если равновесные концентрации
веществ для данной реакции: c(NO) = 1.8 моль/л , c(Cl2) = 1.2 моль/л , c(NOCl) = 0.8 моль/л.

Константу равновесия для данной задачи можно представить в виде 1.64 * 10-1.
© Беллевич Юрий Сергеевич 2018-2023
Данная статья написана Беллевичем Юрием Сергеевичем и является его интеллектуальной собственностью. Копирование, распространение
(в том числе путем копирования на другие сайты и ресурсы в Интернете) или любое иное использование информации и объектов
без предварительного согласия правообладателя преследуется по закону. Для получения материалов статьи и разрешения их использования,
обратитесь, пожалуйста, к Беллевичу Юрию.
2.1. Общее и частичное экономическое равновесие.
Сущность общего (макроэкономического) равновесия
Практически на протяжении всего периода рыночных реформ в России сменяющие друг друга правительства утверждали, что они проводят политику, направленную на достижение макроэкономической стабилизации. В действительности же периоды относительной стабилизации сменяются в России периодами кризисов и стагнаций, затем вновь относительная стабильность, за которой маячит очередной кризис. Возникает вопрос: может ли государство в принципе способствовать стабилизации экономики, и если да, то при помощи каких способов?
Очевидно, что, прежде чем отвечать на эти вопросы, необходимо выяснить параметры того состояния, которое в экономике называют стабильным или равновесным, а также каков механизм достижения подобного состояния.
Понятие равновесия
Равновесие — универсальное понятие, используемое почти во всех точных и естественных науках. Его применяют при анализе сложных систем, в рамках которых отдельные части взаимосвязаны и взаимодействуют. В подобных условиях возникает проблема обеспечения устойчивого и согласованного функционирования всех частей системы. Не является исключением и такая сложная система, как экономика, которая также состоит из множества разнообразных элементов, находящихся между собой во взаимозависимости и в разного рода взаимодействиях, что предполагает наличие определенной согласованности между ними.
Разговор о том, что в экономике «все зависит от всего» начинается с первых шагов по освоению экономической теории. Вспомним, например, модель кругооборота ресурсов, продуктов и дохода. В обыденной жизни такая всеобщая взаимозависимость, пожалуй, нагляднее всего проявляется в периоды нефтяных кризисов. Так было в 70-х годах ХХ в., когда четырехкратное повышение цен на нефть привело не только к росту цен на все энергоносители, но и к сокращению объемов производства, всплеску инфляции, безработицы, к перераспределению доходов. Оно стимулировало также новый виток научно-технического прогресса с характерным для него переходом на ресурсосберегающие технологии.
Подобная «цепочка» зависимостей при колебании цен на нефть наблюдается и в настоящее время — от изменения структуры затрат и доходов в отрасли, всплесков инфляции и безработицы до социальных изменений в отдельных странах и в мировом сообществе в целом.
Анализ условий достижения согласованности взаимозависимых процессов и является предметом теорий, изучающих равновесие в экономике. Равновесие означает не только сбалансированность, но и устойчивость, т.е. либо отсутствуют тенденции к изменению, либо существуют механизмы, восстанавливающие отклонения от равновесия. Теорию экономического равновесия иногда называют теорией экономической статики, в отличие от теорий экономической динамики, к которым относятся теории экономического роста и экономических циклов. При этом анализ равновесия означает не только описание параметров устойчивых состояний, но и причин их нарушения и механизмов восстановления.
Общее равновесие и общие пропорции в экономике
Достижение макроэкономического равновесия возможно в том случае, когда устанавливается пропорциональность и сбалансированность между взаимосвязанными экономическими процессами. Соответствие должно достигаться между следующими параметрами экономических систем:
- производством и потреблением;
- совокупным спросом и совокупным предложением;
- товарной массой и ее денежным эквивалентом;
- сбережениями и инвестициями;
- рынками труда, капитала, потребительских благ и пр.
Достижение соответствия между перечисленными взаимосвязанными параметрами экономической системы будет означать установление так называемых общих пропорций в экономике. Отсутствие равновесия при таком подходе означает, что какие-то сферы экономики не сбалансированы. Нарушение общих пропорций будет проявляться в таких явлениях, как инфляция, безработица, спад производства, уменьшение объема национального продукта и снижение реальных доходов населения.
Частичное равновесие
Анализируя поведение обособленных экономических субъектов — производителей и потребителей на отдельных (локальных) рынках, можно сделать вывод, что стремление фирмы к максимизации прибыли, а потребителя к максимизации полезности приводит к установлению равновесия на отдельно взятых рынках.
О достижении равновесия при таком подходе мы говорим, когда поведение субъектов экономических отношений характеризуется стремлением к достижению равновесия. При этом разнонаправленные силы имеют возможность одинаково воздействовать на ту или иную ситуацию, например взаимодействие спроса и предложения в условиях совершенной конкуренции. Это равновесие может нарушаться в условиях несовершенной конкуренции, когда интересы экономических субъектов, обладающих монопольной властью, превалируют над интересами остальных участников экономического процесса. Анализ подобных ситуаций называется анализом частичного равновесия. Основы анализа частичного равновесия заложены в трудах А. Маршалла.
К частичным пропорциям относится соответствие элементов в рамках отдельных функциональных и организационных компонентов экономической системы. Мы рассматриваем частичные пропорции, когда анализируем спрос и предложение на отдельных рынках товаров и услуг и на рынках факторов производства. Анализ частичного равновесия необходим, но недостаточен, если речь идет о хозяйственной системе в целом.
Стабильность общего равновесия и причины его нарушения
На уровне макроэкономики закономерно возникают вопросы: гарантирует ли достижение частичного равновесия, пусть даже на всех рынках товарных и факторных, достижение общего равновесия в масштабе всей хозяйственной системы; будет ли подобное макроэкономическое равновесие единственно возможным; будет ли оно устойчивым?
Следует отметить, что рассогласование или неравновесие в масштабах всей хозяйственной системы может быть вызвано как обособленностью отдельных ее сфер, порождаемой процессом общественного разделения труда, специализацией и кооперированием, так и динамизмом развития. В этом случае ситуация в экономике постоянно изменяется под воздействием множества разнообразных факторов: технического прогресса, условий производства, спроса и др. Возникают иные представления об оптимальных пропорциях. Отсюда очевидно, что макроэкономическое равновесие, если оно в данное время имеет место, вряд ли будет стабильно. Неизбежно его постоянное нарушение.
Но если так, то возникает вопрос: есть ли смысл «останавливать прекрасное мгновение», есть ли смысл исследовать ситуацию, которая похожа на некий абстрактный труднодостижимый идеал? Ответ сколь очевиден, столь и важен. Подобного рода анализ, как и создание на его основе моделей идеального и реального макроэкономического равновесия, важен, помимо прочего, тем, что он может быть «точкой отсчета», дающей исходные параметры для анализа причин нарушения равновесия — типичной экономической ситуации, которая представляет собой некое постоянное колебание вокруг состояния равновесия. Другими словами, анализ динамичных экономических процессов, которые можно охарактеризовать также как состояние «равновесия — неравновесия», возможен только на основе представлений о параметрах того состояния, которое принято называть общим экономическим равновесием (ОЭР).
Отсюда понятно, почему проблемы частичного и общего равновесия, а также выбор способов и средств обеспечения общего равновесия относятся к числу центральных проблем экономической теории, во многом определяющих ее философскую базу.
Из истории вопроса: Об исследовании процессов экономики
Леон Вальрас о системе общего равновесия
Основателем теории общего экономического равновесия справедливо считают известного швейцарского экономиста Леона Вальраса (1834-1910), которому удалось показать через систему уравнений, как связаны между собой различные рынки в рамках национальной экономики, и математически доказать принципиальную возможность общего равновесия.
Общее равновесие по Вальрасу — это ситуация, при которой равновесие устанавливается одновременно на всех рынках — рынках потребительских благ, денег и труда, а достигается оно в результате гибкости системы относительных цен.
Равновесие на отдельных рынках означает: на рынках потребительских благ спрос и предложение уравновешены так, что у производителей не остается нереализованной продукции, а у потребителей — вынужденных сбережений; на рынке денег равновесие означает, что спрос на деньги со стороны экономических субъектов, т.е. их желание держать деньги в виде наличных или банковских депозитов, равен предложению, т.е. выпущенному банковской системой количеству денег — равновесие между ними обеспечивается гибкой ставкой процента; на рынках труда равновесие между спросом на труд и его предложением регулируется равновесной ставкой реальной заработной платы так, что все желающие могут найти работу.
Перечисленные рынки с одной стороны взаимосвязаны, с другой — достаточно обособлены. Возникают вопросы: каков механизм координации между данными рынками и гарантирует ли он достижение внутренней согласованности между рынками и в экономике в целом?
Л. Вальрас исходил из предположения, что рыночные контракты могут пересматриваться в течение определенного периода времени, и относительные цены (цена одного товара, выраженная в другом) будут меняться при изменении спроса на товар или его предложения. В результате корректировки условий торговли на рынках устанавливается такой набор относительных цен, при которых совпадают желания покупателей купить, а производителей — продать. Иначе говоря, благодаря взаимному согласованию цен и количества товаров и ресурсов нет избыточного спроса и предложения. В конечном виде систему уравнений Вальраса можно представить в следующем виде:
| где | Pi | — | цены конечных товаров и услуг i-го вида; |
| Xi | — | количество товаров и услуг i-го вида; | |
| Uj | — | цены производственных ресурсов j-го вида; | |
| Yj | — | количество производственных ресурсов j-го вида; | |
| m | — | количество конечных товаров и услуг, потребляемых в национальной экономике; | |
| n | — | количество производительных ресурсов, затрачиваемых на производство. |
Данное уравнение можно прокомментировать следующим образом: общее предложение созданных товаров и услуг в денежном выражении должно быть равно общему спросу на них, как сумме доходов, приносимых всеми факторами производства их собственникам.
Вальрас, показав возможность описания экономики через систему уравнений, в которой число уравнений равно числу неизвестных, доказал тем самым принципиальную возможность анализа экономического равновесия.
Описанные Вальрасом условия установления общего равновесия, т.е. неоклассическая модель ценовой координации, хотя и дает возможность объяснить определенные экономические реалии, безусловно, не является всеобъемлющей. Однако это отнюдь не умаляет ее значение.
Работа Вальраса «Элементы политической экономии» (1874 г.) явилась одной из первых работ, развивающих математическое направление в экономических исследованиях. В рамках математического направления экономические идеи формализуются, переводятся на математический язык, что позволяет строить математические модели экономики, с помощью которых обосновываются и проверяются различные теоретические гипотезы и практические рекомендации.
Вальраса часто обвиняют в формализме, говорят о том, что он описал картину, которая ничего не дает, кроме уверенности, что все в конечном итоге образуется. Существуют и иные оценки. Так Блауг пишет, что «вся современная микро- и макроэкономическая теория может рассматриваться как совокупность различных способов придать системе общего равновесия операциональность: в методе частичного равновесия Маршалла… в кейнсианской теории дохода… в леонтьевском анализе «затраты — выпуск». С каждым днем становится все более очевидно, что Шумпетер был прав, назвав «Элементы» Вальраса Великой Хартией современной экономической теории».
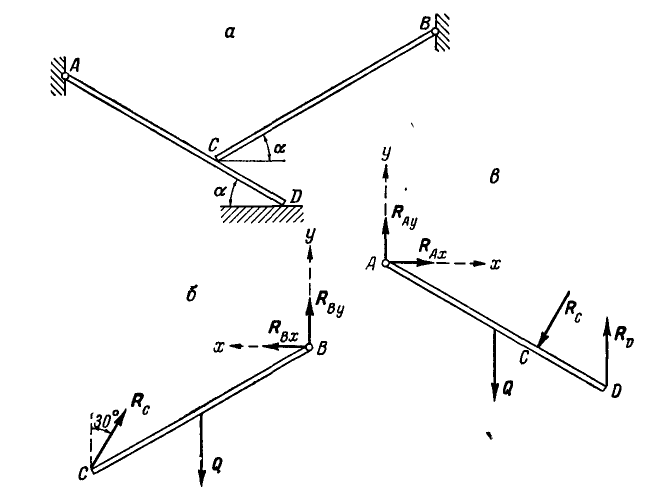
Равновесие систем тел
Под
системой
тел
понимается
конструкция, состоящая из нескольких
твердых
тел, взаимодействующих между собой
через какие-либо связи, допускающие
относительные перемещения этих тел
(они могут соединяться шарнирами,
гибкой нитью, опираться друг на друга
и т.д.).
При
равновесии системы тел как каждое тело,
так и вся система в целом находятся в
равновесии. В связи с этим имеется два
способа решения задач, связанных
с исследованием равновесия системы
тел.
-
Поскольку
каждое тело системы находится в
равновесии, то составляются уравнения
равновесия каждого из тел (тогда
уравнения равновесия системы в целом
могут быть использованы для проверки
правильности решения). -
Сначала
записываются уравнения равновесия
системы в целом, а затем уравнения
равновесия отдельных тел системы (в
этом случае нет необходимости в
составлении уравнений равновесия по
крайней мере одного из тел системы,
но они могут быть применены для проверки).
Замечания:
1.
При составлении уравнений равновесия
всей системы в целом она рассматривается
как абсолютно твердое тело, поэтому в
эти уравнения не войдут силы
взаимодействия между отдельными телами
системы.
2.
Силы, которыми действуют друг на друга
тела системы, в соответствии с аксиомой
о действии и противодействии равны по
модулю и направлены вдоль одной
прямой в противоположные стороны.
Если
несколько тел взаимодействуют в одной
точке, то суммы проекций всех
сил, действующих на эту точку со стороны
контактирующих с ней тел, а также суммы
моментов соответствующих пар сил должны
быть равны нулю.
3. Если внешняя
сила приложена к точке контакта
исследуемых тел, ее следует относить
только к одному из тел системы.
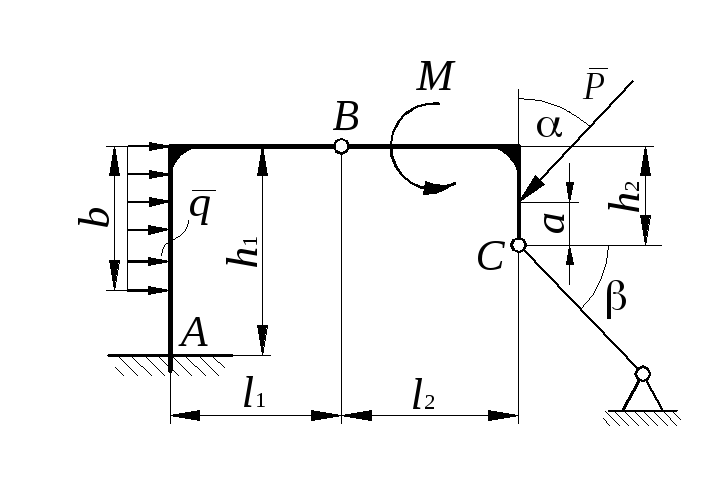
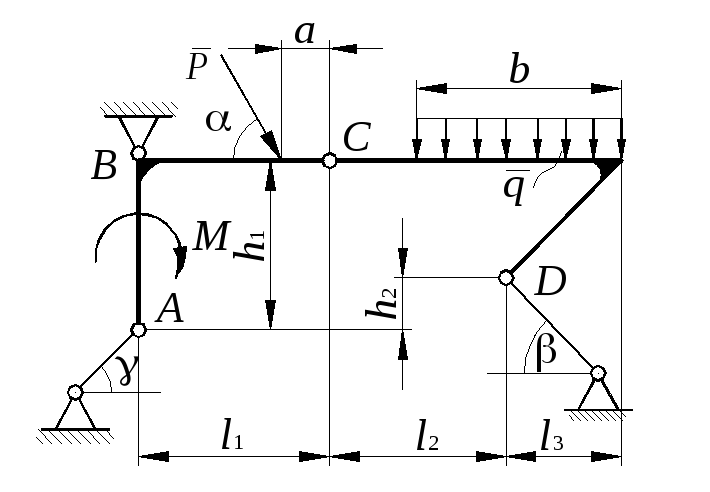
Задание С 4
Найти
реакции опор и давление в промежуточном
шарнире составной конструкции. Схемы
конструкций представлены на рис. С 4
– 1 – С 4 – 5. Размеры – в
м), нагрузка указана в табл. С 4.
Таблица
С 4
|
Вариант (схема) |
|
|
М, кН·м |
q, кН/м |
Вариант (схема) |
|
|
М, кН·м |
q, кН/м |
|
кН |
кН |
||||||||
|
1 |
6,0 |
— |
25,0 |
0,8 |
16 |
8,0 |
11,0 |
31,0 |
0,8 |
|
2 |
5,0 |
8,0 |
26,0 |
— |
17 |
9,0 |
15,0 |
26,0 |
1,1 |
|
3 |
8,0 |
10,0 |
33,0 |
1,1 |
18 |
7,0 |
16,0 |
27,0 |
0,8 |
|
4 |
10,0 |
— |
25,0 |
1,3 |
19 |
6,0 |
18,0 |
35,0 |
1,4 |
|
5 |
12,0 |
— |
27,0 |
1,0 |
20 |
7,0 |
16,0 |
32,0 |
0,8 |
|
Вариант (схема) |
|
|
М, кН·м |
q, кН/м |
Вариант (схема) |
|
|
М, кН·м |
q, кН/м |
|
кН |
кН |
||||||||
|
6 |
14,0 |
12,0 |
— |
0,9 |
21 |
8,0 |
17,0 |
30,0 |
1,2 |
|
7 |
16,0 |
8,0 |
18,0 |
1,4 |
22 |
5,0 |
6,0 |
34,0 |
1,5 |
|
8 |
12,0 |
6,0 |
20,0 |
1,0 |
23 |
14,0 |
10,0 |
36,0 |
1,2 |
|
9 |
14,0 |
— |
28,0 |
1,4 |
24 |
10,0 |
13,0 |
28,0 |
1,3 |
|
10 |
8,0 |
— |
26,0 |
0,9 |
25 |
11,0 |
10,0 |
33,0 |
1,0 |
|
11 |
15,0 |
10,0 |
29,0 |
1,0 |
26 |
15,0 |
15,0 |
18,0 |
1,4 |
|
12 |
15,0 |
8,0 |
28,0 |
1,5 |
27 |
11,0 |
14,0 |
36,0 |
1,5 |
|
13 |
7,0 |
6,0 |
15,0 |
1,1 |
28 |
12,0 |
12,0 |
30,0 |
1,1 |
|
14 |
5,0 |
— |
30,0 |
0,9 |
29 |
10,0 |
9,0 |
35,0 |
1,3 |
|
15 |
6,0 |
10,0 |
24,0 |
1,5 |
30 |
9,0 |
10,0 |
29,0 |
1,5 |
|
1 |
2 |
|
3 |
4 |
|
5 |
6 |
Рис. С 4 – 1
|
7 |
8 |
||
|
9 |
|
10 |
|
|
11 |
12 |
||
|
13 |
14 |
Рис. С 4 – 2
|
15 |
16 |
|
17 |
18 |
|
19 |
20 |
|
21 |
22 |
Рис. С 4 – 3
|
23 |
24 |
|
25 |
26
|
|
27 |
28
|
|
29 |
30 |
Рис. С 4 – 4
Задание С 5
Для заданных систем
тел определить реакции опор и реакции
внутренних связей между телами.
|
1 |
|
|
|
2 |
|
|
|
3 |
|
|
|
4
|
|
Рис. С 5 – 1
|
5 |
|
|
6 |
|
|
7 |
|
|
8 |
|
Рис. С 5 – 2
|
9 |
|
|
|
10 |
|
|
|
11 |
|
|
|
12 |
|
Рис. С 5 – 3
|
13 |
|
|
14 |
|
|
15 |
|
|
16 |
|
|
17 |
|
Рис. С 5 – 4
|
18 |
|
|
|
19 |
|
|
|
20 |
|
|
|
21 |
|
|
|
22 |
|
|
Рис. С 5 – 5
|
23 |
|
|
|
24 |
|
|
|
25 |
|
m = 30 кН·м
АМ = 1 м ВN =ND AC =BD = 2 м
|
|
26 |
|
m = 30 H·м F = 60 H Р = 180 Н АС = 1 м AD = CD
|
Рис. С 5 – 6
|
27 |
|
F = 80 H q =30 H/м Р = 60 Н а =1 м
|
|
28 |
m = 20 Н·м F = 30 Н Р = 40 Н
АК = ВК, СD =2 МN = 4DN =4 м АВ = 4 м |
|
|
29 |
|
m = 50 Н·м F = 120 H Р = 200 Н АD = BD = 2 м BE = ЕС
|
|
30 |
|
m = 18 Н·м q = 10 Н/м F = 20 H P = 12 H AB = 2 м АВ = 2ВС = 2СD
|
Рис. С 5 – 7
Задание С 6
Определить
опорные реакции и реакции в промежуточных
шарнирах составной конструкции от
заданной нагрузки. Варианты задания
показаны на рис. С 6 – 1 – С 6
– 5, а необходимые для решения данные
приведены в табл. С 6.
Таблица С 6
|
Ва-риант |
кН |
кН/м |
М, кН·м |
м |
м |
м |
м |
м |
м |
м |
гр. |
гр. |
гр. |
а, м |
b, м |
|
1 |
4 |
1 |
8 |
10 |
12 |
14 |
– |
– |
– |
– |
30 |
60 |
– |
2 |
9 |
|
2 |
5 |
1,2 |
10 |
9 |
11 |
13 |
15 |
– |
– |
– |
45 |
30 |
60 |
5 |
4 |
|
3 |
6 |
1,4 |
12 |
8 |
10 |
12 |
14 |
– |
– |
– |
30 |
45 |
60 |
6 |
10 |
|
4 |
8 |
1,6 |
16 |
7 |
9 |
11 |
– |
13 |
– |
– |
45 |
30 |
– |
4 |
6 |
|
5 |
10 |
1,8 |
20 |
6 |
8 |
10 |
– |
12 |
6 |
– |
45 |
60 |
– |
8 |
6 |
|
6 |
12 |
2 |
24 |
5 |
7 |
9 |
– |
11 |
5,5 |
– |
60 |
30 |
– |
4,5 |
6 |
|
7 |
14 |
2,2 |
30 |
4 |
6 |
8 |
– |
10 |
5 |
– |
45 |
30 |
60 |
4 |
5,5 |
|
8 |
16 |
2,4 |
32 |
3 |
5 |
– |
– |
9 |
8 |
– |
30 |
60 |
– |
4 |
3,5 |
|
9 |
18 |
2,6 |
40 |
4 |
4 |
– |
– |
8 |
4 |
– |
60 |
45 |
– |
2 |
6 |
|
10 |
20 |
3 |
50 |
3 |
3 |
2 |
– |
7 |
3,5 |
0,5 |
30 |
45 |
60 |
1 |
2 |
|
11 |
4 |
1 |
10 |
14 |
12 |
10 |
– |
16 |
8 |
– |
30 |
60 |
45 |
3 |
16 |
|
12 |
5 |
1,2 |
15 |
9 |
11 |
– |
– |
15 |
7,5 |
4,5 |
30 |
45 |
– |
3 |
7 |
|
13 |
6 |
1,4 |
16 |
12 |
10 |
8 |
– |
14 |
7 |
7,5 |
30 |
60 |
– |
6 |
8 |
|
14 |
8 |
1,6 |
20 |
7 |
9 |
– |
– |
13 |
6,5 |
10 |
45 |
60 |
30 |
4 |
5 |
|
15 |
10 |
1,8 |
30 |
10 |
8 |
6 |
– |
12 |
6 |
3 |
30 |
60 |
45 |
3 |
7 |
|
16 |
12 |
2 |
36 |
7 |
5 |
9 |
– |
11 |
5 |
4,5 |
45 |
30 |
– |
5 |
6 |
|
17 |
14 |
2,2 |
40 |
6 |
4 |
8 |
10 |
10 |
5 |
4 |
45 |
60 |
– |
5 |
6 |
|
18 |
16 |
2,4 |
32 |
5 |
7 |
3 |
– |
9 |
4 |
8 |
30 |
60 |
45 |
2 |
7 |
|
19 |
18 |
2,6 |
42 |
6 |
4 |
2 |
– |
8 |
4 |
6 |
35 |
45 |
60 |
3 |
4,5 |
|
20 |
20 |
3 |
50 |
1 |
3 |
5 |
– |
7 |
– |
– |
30 |
60 |
– |
4,5 |
3 |
|
21 |
4 |
1 |
12 |
10 |
12 |
16 |
– |
10 |
14 |
– |
45 |
30 |
– |
8 |
15 |
|
22 |
5 |
1,2 |
10 |
14 |
9 |
11 |
– |
14 |
15 |
– |
45 |
60 |
30 |
8 |
10 |
|
23 |
6 |
1,4 |
18 |
8 |
10 |
12 |
14 |
14 |
7 |
– |
30 |
60 |
– |
3,5 |
16 |
|
24 |
8 |
1,6 |
18 |
7 |
9 |
– |
– |
6 |
13 |
– |
60 |
– |
– |
3 |
6 |
|
25 |
10 |
1,8 |
20 |
6 |
18 |
– |
– |
6 |
12 |
– |
30 |
– |
– |
9 |
7 |
|
26 |
12 |
2 |
36 |
5 |
7 |
9 |
– |
7 |
9 |
– |
45 |
– |
– |
8 |
6 |
|
27 |
14 |
2,2 |
30 |
4 |
10 |
– |
– |
3 |
6 |
– |
60 |
– |
– |
3 |
5 |
|
28 |
16 |
2,4 |
28 |
4 |
5 |
2 |
– |
2 |
1 |
3 |
30 |
– |
– |
3 |
3 |
|
29 |
18 |
2,6 |
40 |
6 |
4 |
2 |
– |
8 |
4 |
– |
30 |
– |
– |
3 |
4 |
|
30 |
20 |
3 |
46 |
5 |
3 |
2 |
– |
7 |
3 |
– |
60 |
– |
– |
2 |
5 |
|
1 |
2 |
|
3 |
4 |
|
5 |
6 |
|
7 |
8 |
Рис. С 6 – 1
|
9 |
10 |
|
|
11 |
12 |
|
|
13 |
14 |
|
|
15 |
16 |
Рис. С 6 – 2
|
17 |
18 |
|
|
19 |
20 |
|
|
21 |
22 |
|
|
23 |
24 |
Рис. С 6 – 3
|
25 |
26 |
|
|
27 |
28 |
|
|
29 |
|
30 |
Рис. С 6
– 4
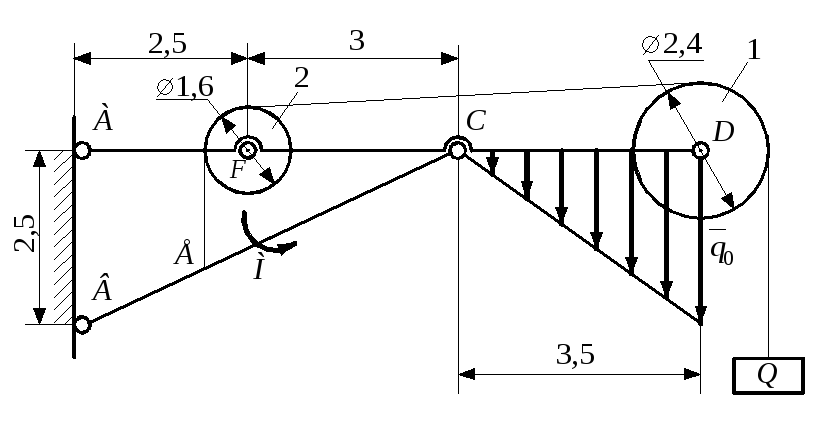
Задание С 7
Невесомые
стрежни AD
и BC
соединены шарниром С
и крепятся к вертикальной стене шарнирами
А
и В.
Груз Q
удерживается невесомой нерастяжимой
нитью, переброшенной через невесомые
неподвижные блоки 1
и 2,
и прикрепленной к стержню ВС
в точке Е.
На стержни действуют сосредоточенная
сила Р,
распределенная нагрузка интенсивности
q
или q0
и пара сил с моментом М.
Определить реакцию в шарнире В.
Данные приведены в табл. С 7.
Примечание.
В вариантах
10–14, 20–29 блок 2 отсутствует.
Таблица С 7
|
Вариант |
Р, |
Q, |
М, |
q, |
q0, |
|
|
– |
10 |
6 |
– |
2 |
|
|
10 |
8 |
– |
– |
– |
|
|
– |
12 |
6 |
– |
2 |
|
|
10 |
10 |
4 |
– |
– |
|
|
2 |
10 |
5 |
– |
– |
|
|
1 |
6 |
4 |
– |
– |
|
|
2 |
3 |
– |
– |
1 |
|
|
– |
10 |
2 |
– |
– |
|
|
– |
12 |
– |
– |
1,5 |
|
|
10 |
10 |
– |
2 |
– |
|
|
– |
6 |
4 |
– |
2 |
|
|
6 |
10 |
4 |
2 |
– |
|
|
2 |
6 |
5 |
2 |
– |
|
|
5 |
8 |
4 |
1,5 |
– |
|
|
5 |
6 |
3 |
– |
– |
|
|
3 |
4 |
– |
– |
– |
|
|
– |
5 |
– |
– |
2 |
|
|
– |
4,5 |
6 |
2 |
– |
|
|
– |
8 |
5 |
– |
2 |
|
|
6 |
10 |
4 |
– |
3 |
|
|
5 |
8 |
5 |
2 |
– |
|
|
– |
10 |
3 |
1 |
– |
|
|
– |
8 |
4 |
– |
1,5 |
|
|
4 |
10 |
5 |
2,5 |
– |
|
|
5 |
10 |
2 |
– |
3 |
|
|
6 |
10 |
– |
– |
3 |
|
|
4 |
10 |
– |
– |
2 |
|
|
– |
5 |
3 |
2 |
– |
|
|
– |
10 |
2 |
– |
3 |
|
|
2 |
10 |
5 |
– |
– |
|
1 |
|
|
2 |
|
|
3 |
|
Рис. С 7
– 1
|
4 |
|
5 |
|
6 |
Рис. С 7
– 2
|
7 |
|
8 |
|
9 |
Рис. С 7
– 3
|
10 |
|
11 |
|
12 |
Рис. С 7
– 4
|
13 |
|
|
14 |
|
|
15 |
|
Рис. С 7
– 5
|
16 |
|
17 |
|
18 |
Рис. С 7
– 6
|
19 |
|
20 |
|
21 |
Рис. С 7
– 7
|
22 |
|
23 |
|
24 |
Рис. С 7
– 8
|
25 |
|
|
26 |
|
|
27 |
|
Рис. С 7
– 9
|
28 |
|
|
29 |
|
|
30 |
|
Рис. С 7
– 10
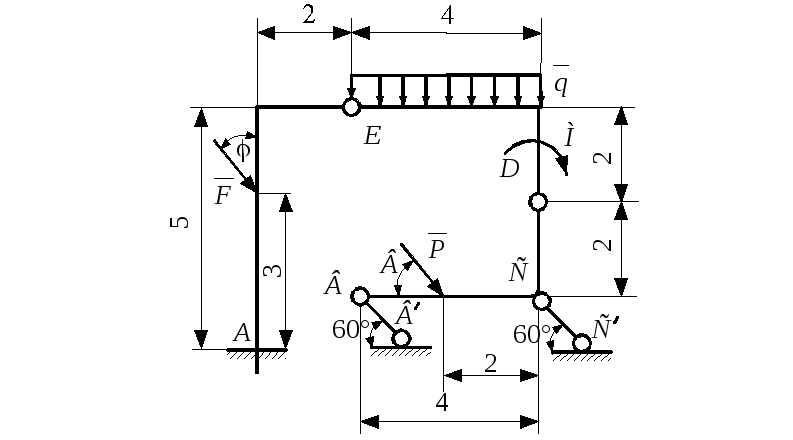
Задание С 8
Два
невесомых стержня АС
и СD,
соединенные между собой шарниром С,
находятся в равновесии под действием
сосредоточенной силы Р,
пары сил с моментом М
и распределенной нагрузки, изменяющейся
по закону q = q(s).
Определить реакции в заделке А
и усилие в невесомом стержне ВD.
Данные приведены в табл. С 8.
Направление
оси s
показано на чертеже. Начало отсчета для
вариантов 1, 2, 4, 8, 10–14, 22, 24, 26, 28 – в точке
А;
для вариантов 3, 5, 15, 16, 18-20, 27, 29 в точке
С;
для вариантов 6, 7, 9, 21, 23, 25 – в точке D;
для варианта 17 – в точке Е.
Для вариантов 2, 8 коэффициент К=1
м.
Таблица С 8
|
Вариант |
Р, кН |
М, кН·м |
q(S) |
q0, кН |
q01, кН |
q02, кН/м2 |
q03, кН/м3 |
|
1 |
4 |
4 |
0 |
— |
— |
— |
1 |
|
2 |
— |
2 |
0 |
— |
1 |
— |
— |
|
3 |
— |
4 |
0 |
1 |
— |
— |
— |
|
4 |
4 |
3 |
0 |
— |
1 |
0,5 |
— |
|
5 |
4 |
2 |
0 |
— |
1 |
— |
1 |
|
6 |
— |
4 |
0 |
— |
1 |
1 |
1 |
|
7 |
— |
4 |
0 |
— |
— |
1 |
1 |
|
8 |
6 |
4 |
0 |
— |
1 |
— |
— |
|
9 |
— |
6 |
0 |
— |
1 |
— |
1 |
|
10 |
— |
6 |
0 |
1 |
— |
— |
— |
|
Вариант |
Р, кН |
М, кН·м |
q(S) |
q0, кН |
q01, кН |
q02, кН/м2 |
q03, кН/м3 |
|
11 |
— |
6 |
0 |
— |
— |
— |
1 |
|
12 |
10 |
4 |
0 |
— |
— |
— |
1 |
|
13 |
— |
8 |
0 |
— |
1 |
— |
1 |
|
14 |
— |
4 |
0 |
1 |
— |
— |
— |
|
15 |
10 |
— |
0 |
— |
1 |
— |
1 |
|
16 |
— |
4 |
0 |
— |
— |
— |
1 |
|
17 |
— |
4 |
0 |
— |
— |
— |
1 |
|
18 |
6 |
4 |
0 |
— |
— |
— |
1 |
|
19 |
— |
6 |
0 |
— |
— |
1 |
1 |
|
20 |
— |
4 |
0 |
1 |
— |
— |
— |
|
21 |
— |
4 |
0 |
— |
— |
1 |
1 |
|
22 |
10 |
4 |
0 |
1 |
— |
— |
— |
|
23 |
— |
4 |
0 |
— |
2 |
— |
— |
|
24 |
10 |
— |
0 |
1 |
— |
— |
— |
|
25 |
2 |
4 |
0 |
— |
— |
— |
1 |
|
Вариант |
Р, кН |
М, кН·м |
q(S) |
q0, кН |
q01, кН |
q02, кН/м2 |
q03, кН/м3 |
|
26 |
10 |
4 |
0 |
— |
2 |
— |
— |
|
27 |
10 |
4 |
0 |
— |
— |
— |
1 |
|
28 |
10 |
6 |
0 |
— |
1 |
— |
1 |
|
29 |
4 |
4 |
0 |
— |
1 |
— |
1 |
|
30 |
150 |
100 |
20 |
— |
— |
— |
— |
|
1. |
2 |
|
|
3. |
4. |
|
|
5. |
6 |
|
Рис. С 8
– 1
|
7. |
8. |
|
9. |
10.
|
|
11. |
12. |
|
13. |
14. |
Рис. С 8
– 2
|
15. |
16. |
|
17. |
18. |
|
19. |
20. |
|
21. |
22. |
Рис. С 8
– 3
|
23. |
24. |
|
25. |
26. |
|
27. |
28. |
|
29. |
30. |
Рис. С 8
– 4
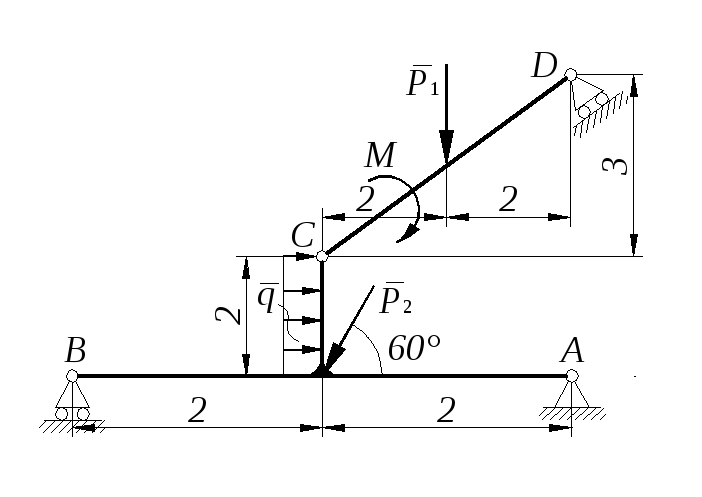
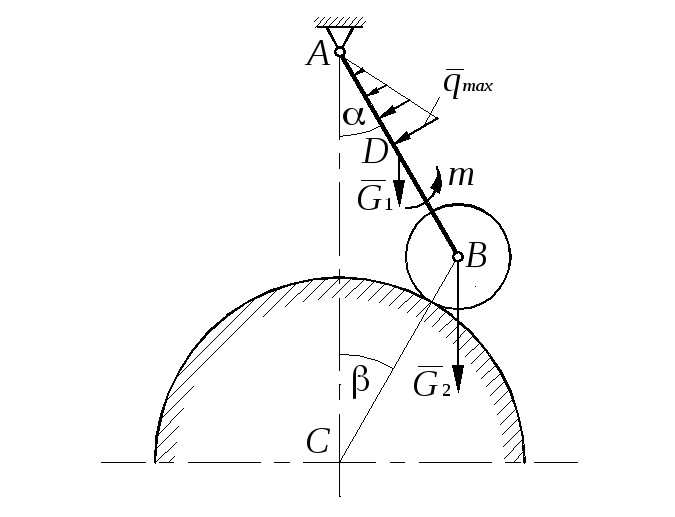
Задание С 9
Жесткая
рама представленная на рис. С9 – 1 и С9
– 6, состоящая из трех соединенных между
собой связями конструкций крепится с
помощью внешних опор, указанных на
рисунках к фундаменту.
На
конструкции действуют: пара сил с
моментом М,
равномерно распределенная нагрузка
интенсивностью
и силы
,
составляющие с элементами конструкции
соответственно углыи
.
Значение
момента М
пары сил, интенсивности
распределенной нагрузки, сил
и
,
а так же углови
указаны в табл. С 9.
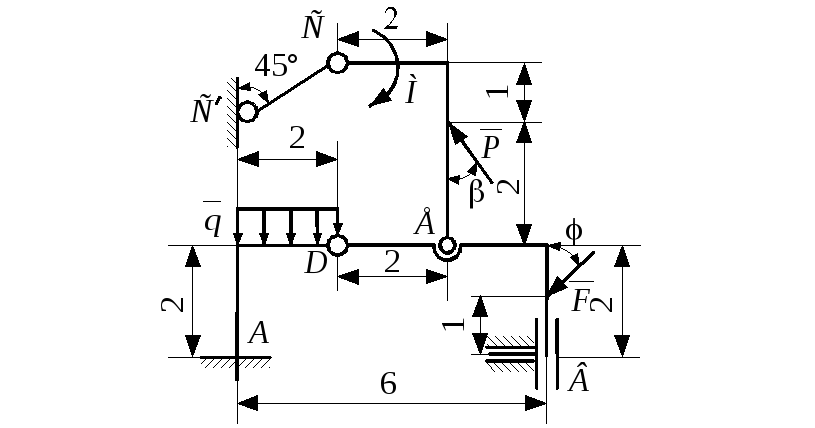
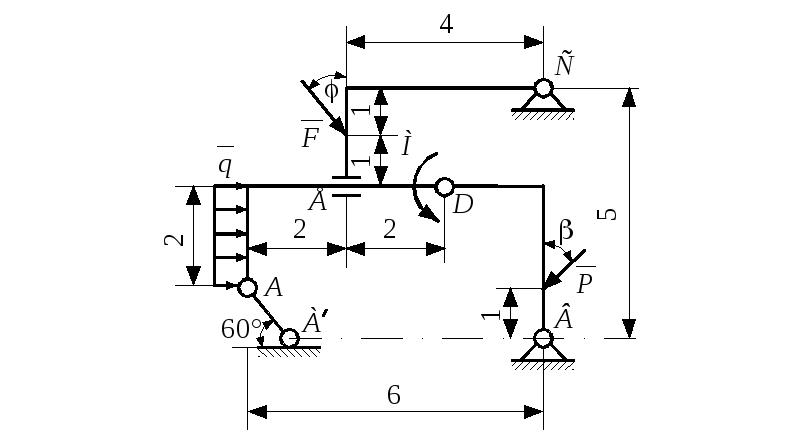
Определить
давления рамы на внешние опоры, а так
же усилия в связях соединяющих конструкции
между собой в раму вызванные заданными
нагрузками.
Таблица
С 9
|
Вариант |
Нагрузка |
|||||
|
М |
q |
P |
F |
|
|
|
|
кН ∙ м |
кН/м |
кН |
кН |
град. |
град. |
|
|
|
8 |
1 |
12 |
20 |
60 |
75 |
|
|
6 |
4 |
6 |
18 |
45 |
135 |
|
|
12 |
2 |
40 |
10 |
15 |
30 |
|
|
4 |
3 |
25 |
18 |
30 |
45 |
|
|
7 |
6 |
12 |
24 |
75 |
60 |
|
|
12 |
5 |
6 |
30 |
15 |
120 |
|
|
10 |
0,8 |
8 |
14 |
45 |
15 |
|
|
6 |
1,6 |
4 |
8 |
30 |
45 |
|
|
5 |
4 |
12 |
26 |
60 |
75 |
|
|
3 |
1 |
5 |
4 |
45 |
30 |
|
|
7 |
2 |
12 |
14 |
30 |
45 |
|
|
13 |
4 |
16 |
8 |
15 |
60 |
|
|
17 |
6 |
8 |
12 |
165 |
30 |
|
|
6 |
0,5 |
9 |
23 |
120 |
45 |
|
|
14 |
3 |
5 |
10 |
45 |
30 |
|
|
5 |
2 |
7 |
5 |
60 |
75 |
|
|
3 |
4 |
11 |
4 |
30 |
15 |
|
|
4 |
7 |
20 |
12 |
30 |
45 |
|
|
8 |
8 |
19 |
6 |
15 |
75 |
|
|
9 |
6 |
8 |
16 |
30 |
120 |
|
|
11 |
4 |
14 |
15 |
105 |
45 |
|
|
15 |
12 |
17 |
12 |
15 |
135 |
|
|
7 |
5 |
7 |
18 |
45 |
15 |
|
Вариант |
Нагрузка |
|||||
|
М |
q |
P |
F |
|
|
|
|
кН ∙ м |
кН/м |
кН |
кН |
град. |
град. |
|
|
|
6 |
4 |
5 |
6 |
60 |
105 |
|
|
9 |
3 |
4 |
4 |
30 |
75 |
|
|
8 |
7 |
2 |
12 |
45 |
30 |
|
|
4 |
6 |
3 |
6 |
60 |
30 |
|
|
17 |
2 |
6 |
17 |
120 |
75 |
|
|
21 |
4 |
8 |
20 |
30 |
15 |
|
|
6 |
5 |
9 |
7 |
75 |
60 |
|
1 |
2 |
|
3 |
4 |
Рис.
С 9 – 1
|
5 |
6 |
|
7 |
8 |
|
9 |
10 |
Рис.
С 9 – 2
|
11 |
12 |
|
13 |
14 |
|
15 |
16 |
Рис.
С 9 – 3
|
17 |
18 |
|
19 |
20 |
|
21 |
22 |
Рис.
С 9 – 4
|
23 |
24 |
|
25 |
26 |
|
27 |
28 |
Рис.
С 9 – 5
|
29 |
|
30 |
|
Рис.
С 9 – 6
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Раздел 2. Теория производства
Цель: выяснить, что представляет собой общее экономическое равновесие.
- раскрыть условия общего экономического равновесия и этапы его анализа;
- построить систему уравнений общего экономического равновесия;
- исследовать условия эффективности обмена;
- исследовать условия эффективности распределения ресурсов;
- раскрыть условия эффективного выпуска продукции;
- разобраться в понятии «квазиоптимум».
Оглавление
6.1. Анализ общего равновесия
В предыдущих темах рассматривались рынки потребительских товаров, рынки факторов производства, т. е. равновесие, складывающееся на отдельных рынках – частичное равновесие . В действительности все рынки взаимосвязаны, взаимодействуя друг с другом. Равновесие, возникающее в результате взаимодействия всех рынков, когда изменение спроса или предложения на одном рынке влияет на равновесные цены и объемы продаж на всех рынках, называется общим экономическиме равновесием .
Таким образом, при анализе общего равновесия рассматриваются экономические взаимозависимости всех цен и решений.
На передний план выходят взаимодополняемость и взаимозаменяемость различных товаров. Поэтому анализ общего равновесия включает следующие этапы:
- первичное изменение;
- влияние первичного изменения на рынки дополняющих товаров;
- влияние первичных изменений на рынки заменяющих товаров;
- эффект обратной связи.
Взаимосвязь товарных рынков может быть записана системой уравнений. Первым попытался сделать это Л. М. Вальрас. В рыночной экономике цены предопределяют объем выпускаемой продукции, а объем выпуска в значительной степени предопределяет цены. Цены потребительских товаров зависят от цен на ресурсы, а цены ресурсов – от цен потребительских благ, на которые существует спрос. Выйти из этого «замкнутого круга» Л. М. Вальрас считал возможным, решая всю систему уравнений одновременно:
где А – показатель реальных активов страны, отражающий ее богатство;
М – количество наличных денег.
Если известны А и М, то число уравнений равно числу неизвестных. Подставив реальные значения цен, в результате получим количества обмениваемых товаров.
Во времена Вальраса отсутствовал математический аппарат для решения такой системы. Поэтому он предлагал группировку уравнений, а путь к равновесию рассматривал как постепенный процесс – поиск «ощупью» верных пропорций обмена.
На этой основе В. В. Леонтьев создал модель «затраты-выпуск» – матрицу затрат и результатов, за которую получил Нобелевскую премию.
6.2. Эффективность обмена
Общее равновесие в экономике показывает взаимосвязь всех сделок, и следовательно, всех людей, живущих во многих странах мира. При этом производство осуществляется ради обмена: производя один товар, люди в обмене получают массу других, необходимых им.
Таким образом обмен приносит выгоду всем участникам сделок – в этом великая миссия рынка.
К. Менгер писал, что нельзя говорить об эквивалентности в обмене, т. к. выигрывают оба участника сделки.
Отсюда – очередная задача состоит в анализе эффективности обмена.
Возьмем, к примеру, двух человек – Антона и Бориса.
8 тюбиков зубной пасты
3 тюбика зубной пасты
11 тюбиков зубной пасты
Поскольку у Антона мало мыла и много пасты, он заинтересован в обмене. Предположим, он готов отдать за 1 кусок мыла 3 тюбика зубной пасты, т. е. MRS А м,п=1/3.
У Бориса мало зубной пасты. Он готов отдать 3 куска мыла за 1 тюбик пасты, т. е. MRS Б м,п=3/1.
Если при сделке удастся обменять 1 тюбик пасты на 1 кусок мыла, то выиграют оба: Антон за 1 кусок мыла отдаст не 3 тюбика пасты, а 1; Борис за 1 тюбик пасты отдаст не 3 куска мыла, а 1.
Сделка эффективна, т. к. оба были готовы на большие «жертвы». Таким образом, при том же количестве товаров выгоду получили оба.
Итак, если предельные нормы замены у участников сделки различаются, то существует возможность взаимовыгодного обмена, повышения его эффективности. Если же выполняется равенство:
т. е. предельные возможности обмена мыла на зубную пасту у обоих контрагентов равны, дальнейший обмен не эффективен.
При этом оптимум потребителя предполагает также учет цен мыла и зубной пасты, следовательно, выполняется равенство:
Для более тщательного исследования этого процесса, определения наиболее эффективных объемов обмена используется «коробка Эджуорта» , в которой заключены имеющиеся товары и фиксируются кривые безразличия, т. е. кривые равных полезностей для 2 контрагентов сделки. Точки касания кривых безразличия характеризуют Парето-оптимальное распределение благ . Это такое состояние экономики, при котором невозможно изменить распределение благ так, чтобы увеличилось их количество у какого-либо одного потребителя без уменьшения благосостояния других.
6.3. Эффективность производства
При данных ресурсах и технологии, чем больше производится одного товара, тем в данный момент меньше возможность производства других товаров.
Предположим, что в производстве используется 60 час. труда (L) и 40 час. машинного времени (К). Тогда ресурсное ограничение можно записать так:
По аналогии с предшествующим материалом можно утверждать, что парето-оптимальное распределение ресурсов достигается тогда, когда уже невозможно их перераспределить так, чтобы увеличить выпуск одного блага, не уменьшив выпуска другого.
Предельная норма замены-трансформации мыла зубной пастой MRT м,п в данном случае характеризует возможность переброски ресурсов из производства мыла в производство зубной пасты.
По мере роста производства зубной пасты MRT возрастает, поскольку все труднее переместить ресурсы из производства мыла в производство пасты.
Продолжим исследование, используя понятие альтернативных издержек или издержек упущенных возможностей . В таком случае предельные издержки зубной пасты выражаются в отказе от дополнительной единицы мыла, следовательно, МСп=-Δм. И наоборот, предельные издержки мыла МСм=-Δп. То есть:
И, наконец, следующая задача – определить эффективный выпуск продукции , соединив эффективность обмена и эффективность производства.
Выпуск будет эффективным, если он:
- не выходит за пределы имеющихся ресурсов;
- будет максимизировать полезность для покупателей при имеющимся количестве благ, т. е. выполняется равенство:
Следовательно, можно сделать вывод, что эффективность выпуска диктует определенные требования к ценам – они должны одновременно отражать предельные полезности для потребителей и предельные издержки на производство. Лишь в условиях совершенной конкуренции цена отвечает этим требованиям.
6.4. Общее равновесие в случаях отклонений от нормальных рыночных условий
Рассмотрим два варианта.
Первый вариант: производство зубной пасты монополизировано, а мыло по-прежнему производится в условиях совершенной конкуренции.
Таким образом, MRSм,п>MRTм,п, т. е. условие общего равновесия нарушено.
Поскольку потребители руководствуются ценами рынка, они при росте цен на монополизированный продукт сокращают его потребление (объем спроса). Освобождающиеся в монополизированном производстве зубной пасты ресурсы перетекают в производство мыла. Это приводит к перепроизводству мыла и снижению его цены.
Следовательно, существование монополии искажает цены, во-первых, в монополизированном производстве (рост цен и недопроизводство зубной пасты) и, во-вторых, во всех других отраслях (перепроизводство мыла и падение цены).
Таким образом, распределение ресурсов искажается на всех рынках, даже если монополия существует только на некоторых. Общее равновесие нарушается.
Другое искажение может быть вызвано налогом.
Второй вариант: производство (и продажа) мыла облагается налогом, а зубной пасты – не облагается.
Налог непосредственно выплачивают продавцы-производители. В итоге происходит сдвиг влево-вверх кривой предложения. Это приводит к росту равновесной цены. Покупатели оплачивают розничную цену с налогом – p tax м, а чистая цена производителя – без налога.
Следовательно, MRSм,п>MRTм,п, т. е. условие общего экономического равновесия нарушено.
В реальной действительности возможно совпадение обоих случаев. Если производство зубной пасты монополизировано, а производство мыла осуществляется в условиях совершенной конкуренции, то можно прибегнуть к налоговой политике, пытаясь восстановить нарушенное равновесие.
Если благодаря налогу удастся поднять цены на мыло, приток дополнительных ресурсов в эту отрасль прекратится и может даже возникнуть ситуация давления на отрасль, в которой господствует монополия.
Общее экономическое равновесие достигается на новом уровне – уровне квазиоптимума . Теория квазиоптимума утверждает, что в случае, когда в одной отрасли (или группе отраслей) отклонения от нормальных рыночных условий не могут быть устранены, лучше отказаться от достижения максимальной эффективности в других отраслях с тем, чтобы сбалансировать экономику в целом.
Достигнутый квазиоптимум компенсирует искажение на рынке, вызванное монополией, другим искажением (в данном случае налогом) на другом рынке, на котором в противном случае была бы достигнута эффективность. Конечный результат – увеличение производства зубной пасты и сокращение производства мыла, т. е. ресурсы распределяются примерно так, как в условиях совершенной конкуренции.
Выводы
- Равновесие, возникающее в результате взаимодействия всех рынков, когда изменение спроса или предложения на одном рынке влияет на равновесные цены и объемы продаж на всех рынках, называется общим экономическим равновесием. Анализ общего равновесия включает следующие этапы: первичное изменение, влияние первичного изменения на рынки дополняющих товаров, влияние первичных изменений на рынки заменяющих товаров, эффект обратной связи. Взаимосвязь товарных рынков может быть записана системой уравнений.
- Эффективность обмена достигается тогда, когда предельные нормы замены одного товара другим у участников сделки равны. Парето-оптимальное распределение благ — это такое состояние экономики, при котором невозможно изменить распределение благ так, чтобы увеличилось их количество у какого-либо одного потребителя без уменьшения благосостояния других.
- При данных ресурсах и технологии, чем больше производится одного товара, тем в данный момент меньше возможность производства других товаров. Парето-оптимальное распределение ресурсов достигается тогда, когда уже невозможно их перераспределить так, чтобы увеличить выпуск одного блага, не уменьшив выпуска другого.
- Выпуск продукции будет эффективным, если он: 1) не выходит за пределы имеющихся ресурсов; 2) будет максимизировать полезность для покупателей при имеющемся количестве благ. Таким образом, эффективность выпуска диктует определенные требования к ценам – они должны одновременно отражать предельные полезности для потребителей и предельные издержки на производство. Лишь в условиях совершенной конкуренции цена отвечает этим требованиям.
- Теория квазиоптимума утверждает, что в случае, когда в одной отрасли (или группе отраслей) отклонения от нормальных рыночных условий не могут быть устранены, лучше отказаться от достижения максимальной эффективности в других отраслях с тем, чтобы сбалансировать экономику в целом. Достигнутый квазиоптимум компенсирует искажение на рынке, вызванное, к примеру, монополией, другим искажением (к примеру, налогом) на другом рынке, на котором в противном случае была бы достигнута эффективность. Конечный результат – ресурсы распределяются примерно так, как в условиях совершенной конкуренции.
Вопросы для самопроверки
- Что представляет собой общее экономическое равновесие?
- Какие этапы включает в себя анализ общего экономического равновесия?
- Как строится система уравнений общего экономического равновесия?
- При каких условиях достигается эффективность обмена?
- Что означает Парето-оптимальное распределение благ?
- Что означает Парето-оптимальное распределение ресурсов и каковы его условия?
- При каких условиях достигается эффективный выпуск продукции?
- Что означает понятие «квазиоптимум»?
Литература
- Экономическая теория: Учебник / Под общ. ред. акад. В. И. Видяпина, А. И. Добрынина, Г. П. Журавлевой, Л. С. Тарасевича. – изд. испр. и доп.– М.: ИНФРА-М, 2005. – С. 217-231.
- Экономикс: принципы, проблемы и политика: Учеб. пособие. Т. 2 / К. Р. Макконнелл, С. Л. Брю. – М.: Республика, 1996. – С. 12-29.
- Павлова И. П. Микроэкономика: Электронное учеб. пособие. – СПб.: РИЦ МБИ, 2006.
- Павлова И. П. Микроэкономика. Опорный конспект: рабочая тетрадь. – СПб.: РИЦ МБИ, 2006.
- Нуреев Р. М. Курс микроэкономики: Учебник для вузов. – 2-е изд. – М.: Норма, 2005. – С. 80-95.
- Гальперин В. М., Игнатьев С. М., Моргунов В. М. Микроэкономика: Учебник: в 2 т. Т. 1 / Под ред. В. М. Гальперина. – 1998. – С. 39-65.
iSopromat.ru
Уравнения равновесия (статики) характеризуют неподвижность заданной системы нагруженной комплексом внешних усилий.
При решении задач теоретической механики и сопротивления материалов (например, при определении опорных реакций или внутренних силовых факторов) исходя из условия неподвижности системы или ее частей, записываются уравнения равенства нулю сумм проекций всех сил на оси выбранной системы координат
что следует из условия отсутствия перемещения системы вдоль этих осей, и сумм моментов относительно произвольных точек системы
из условия отсутствия ее вращения относительно указанных осей.
Надо отметить что в случае действия плоской системы сил можно получить только три уравнения статики, а линейная схема нагружения позволяет записать лишь одно уравнение.
Пример составления уравнений равновесия
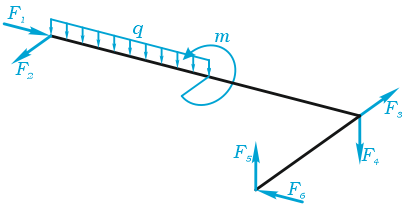
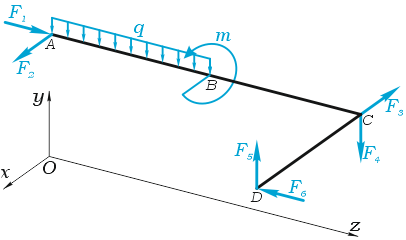
В качестве примера, рассмотрим общий случай пространственного нагружения, где комплекс усилий, включающий сосредоточенные силы F1-F6, равномерно распределенную нагрузку q, и момент m расположенный в плоскости перпендикулярной длинному стержню, удерживает L-образную систему в равновесии.
Обозначим характерные точки системы буквами A, B, C и D, зададим положение трехмерной системы координат xyz и запишем уравнения равновесия.
Суммы проекций сил
Сумма проекций всех сил на ось x (с учетом правила знаков для сил):
здесь при записи силы от распределенной нагрузки ее интенсивность q умножается на ее длину AB.
Суммы моментов
Суммы моментов всех нагрузок, например, относительно точки B (с учетом правила знаков для моментов):
Из полученных шести уравнений можно определить не более шести неизвестных усилий.
Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах
Равновесие системы, состоящей из нескольких тел в теоретической механике
Равновесие системы, состоящей из нескольких тел:
До сих пор мы рассматривали равновесие одной материальной точки или одного твердого тела, находящихся под действием сил. При этом мы видели, что для одной точки можно составить два уравнения равновесия
На практике же часто приходится иметь дело с системами, состоящими из нескольких материальных точек или твердых тел, соединенных между собой связями. Примерами таких систем могут служить машины, составленные из отдельных деталей, соединенных определенным образом между собой, сооружения, состоящие из отдельных блоков и пр.
На каждое из таких находящихся в равновесии тел действуют силы, часть которых представляет собой действие остальных тел системы на рассматриваемое и подлежит определению.
Так как при этом силы, действующие на каждое тело, вообще говоря, не пересекаются в одной точке, то для определения реакций связей в местах соприкасания тел с другими телами системы и связями можно для каждого из тел, входящих в систему, составить 3 уравнения равновесия, а для системы 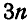
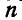
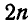
Может оказаться при этом, что число неизвестных, подлежащих определению, превысит общее число уравнений равновесия статики, тогда такая задача не может быть решена приемами статики и называется задачей статически неопределимой.
Определение неизвестных реакций связей выясним на отдельных примерах.
Задача №1
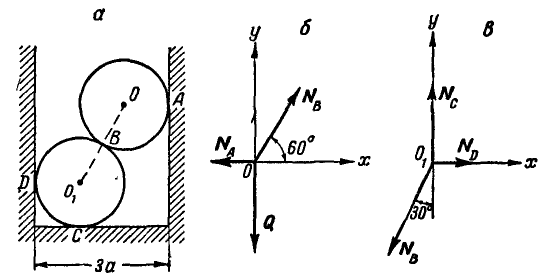
Два одинаковых однородных цилиндра весом Q = 60 кГ каждый (рис. 57, а) соприкасаются между собой в точке В и удерживаются в равновесии двумя вертикальными и горизонтальной плоскостями. Радиус каждого из цилиндров равен а. Пренебрегая трением между цилиндрами и плоскостями, найти реакции 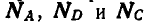
Решение. Соединяя центры цилиндров 
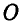
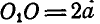
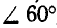
Рассмотрим сначала равновесие верхнего цилиндра (рис. 57, б):.
Отсюда получаем:
Обе реакции получились, со знаком 
Отсюда получаем:
Эту задачу можно было бы решить геометрическим способом, построив треугольники равновесия для каждого из цилиндров.
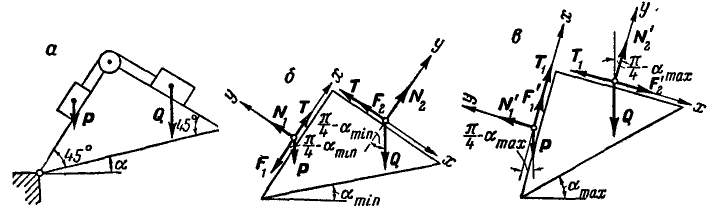
Задача №2
При каком наибольшем и наименьшем угле 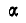
Решение. Рассмотрим сначала предельный случай равновесия грузов Р и Q, когда 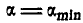
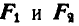
Уравнения равновесия груза Р будут:
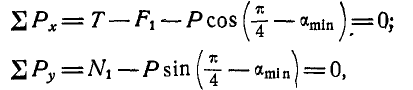
Точно так же уравнения равновесия для груза Q будут:
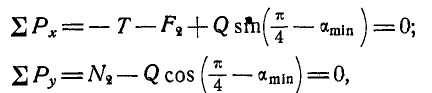
Подставляя вместо 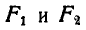
Складывая первые два уравнения и подставляя вместо 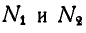
Для нахождения 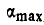
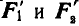
Задача №3
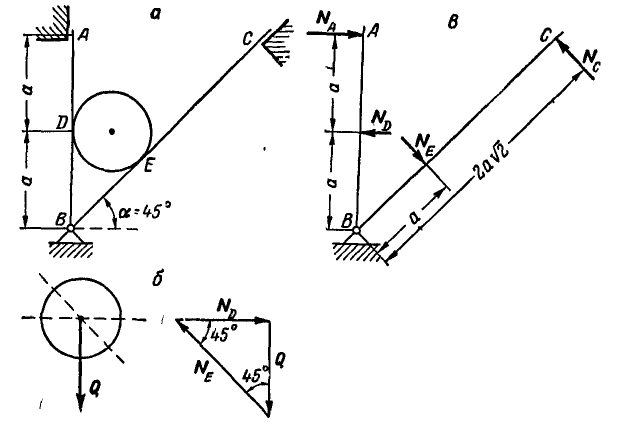
Два однородных бруска AD и СВ одинаковой длины и одинакового веса Q=60 кГ каждый наклонены к горизонтальной прямой под 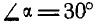
Решение. Рассмотрим равновесие каждого из брусков в отдельности. Составляя сначала уравнения равновесия сил для бруска СВ (рис. 60, б), имеем:
а затем для бруска AD (рис. 60, в):
Длина бруска 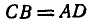
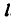
После решения уравнений получаем:
Задача №4
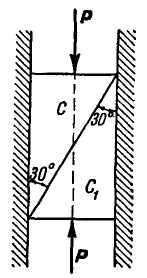
Однородный цилиндр весом Q = 60 кГ опирается свободно на вертикальную и наклонную плоскости АВ и ВС (рис. 61, а). В точках А и С плоскости опираются на гладкие опоры, расположенные на одной горизонтали. Найти давления 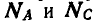
Решение. Рассмотрим сначала равновесие цилиндра (рис. 61, б) и, построив для него треугольник равновесия, находим: 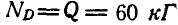
Теперь уже можно перейти к рассмотрению равновесия плоскостей ВА и ВС (рис. 61, в). Для определения давлений в точках А и С освободимся от связей и взамен них введем реакции 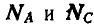
откуда
Мы нашли реакции связей в точках А и С; давления же в этих точках, численно равные реакциям связей, будут направлены в противоположные реакциям 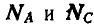
Задача №5
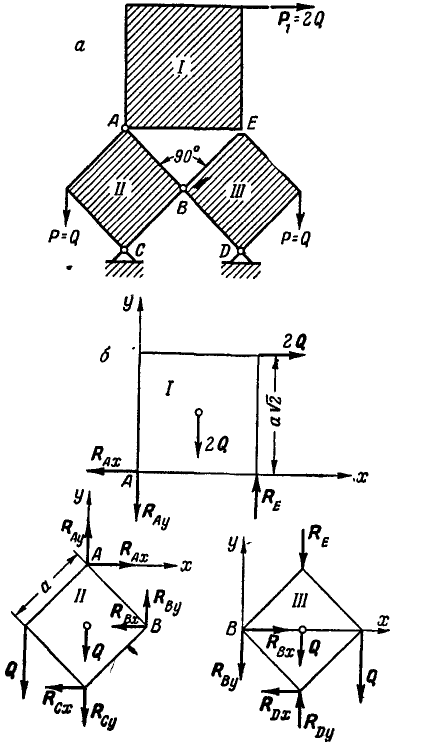
Система состоит из трек однородных квадратных пластинок I, II и III, соединенных в точках А, В, С и D шарнирно (рис. 62, а). Вес каждой из пластинок II и III равен Q кГ. Зная, что веса пластинок пропорциональны их площадям, найти реакции связей в шарнирах С и D, пренебрегая трением.
Решение. Общее число неизвестных сил равно девяти, так как каждый из неподвижных шарниров А, В, С и D дает по две неизвестные составляющие реактивные силы, а девятая реактивная сила, известная по направлению, возникает в точке Е, Для определения девяти неизвестных необходимо иметь девять уравнений, которые мы получим, если рассмотрим в отдельности равновесие каждой из пластинок I, II и III (рис. 62, б).
На чертеже указано направление действующих на каждую из пластинок сил.
Составляя для каждой из пластинок по три уравнения равновесия, имеем:
для пластинки
для пластинки
для пластинки
Решая полученные девять уравнений с девятью неизвестными, находим:
Все модули реакций получились со знаком плюс. Если бы некоторые из найденных модулей получились со знаком минус, то направление стрелок соответствующих реакций пришлось бы изменить на обратное тому, которое было принято при решении задачи.
| Рекомендую подробно изучить предмет: |
|
| Ещё лекции с примерами решения и объяснением: |
- Графостатика в теоретической механике
- Расчет ферм
- Пространственная система сходящихся сил
- Момент силы относительно точки и относительно оси
- Векторное исчисление
- Виды связей
- Параллельные силы
- Произвольная плоская система сил
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
источники:
http://isopromat.ru/sopromat/otvet/uravnenia-statiki
http://www.evkova.org/ravnovesie-sistemyi-sostoyaschej-iz-neskolkih-tel-v-teoreticheskoj-mehanike


























































 СЕ = ED
СЕ = ED