Рассмотрим
два непустых множества А
и В.
Элементы этих множеств могут каким-либо
образом сопоставляться друг другу,
образуя пары (а,
b).
Если задан способ такого сопоставления,
то говорят, что между множествами
установлено соответствие. При этом
совершенно необязательно, чтобы в
сопоставлении участвовали все элементы
множеств А и В.
Соответствием
между множествами А и В называется любое
подмножество G
АВ
– декартово произведения этих множеств.
Множество
А иногда называют областью
отправления соответствия
G,
а множество В – областью
прибытия.
График
этого соответствия – множество
упорядоченных
пар (а,
b)
соответствия G.
Обозначается
соответствие так:
G:
AB
или G
АВ
= {(a,
b)aA,
bB,
(a,
b)G}.
Первой
проекцией
или областью
определения
соответствия G
называется множество всех первых
компонентов пар (а,
b)G.
Обозначается
пр1
G или
Dom(G)
= {a
aA,
(а,
b)G}.
Второй
проекцией
или областью
значений
соответствия G
называется множество всех вторых
компонентов пар (а,
b)G.
Обозначается
пр2
G
или
Im(G)
= {bbB,
(а,
b)G}.
Каждый
элемент bB,
соответствующий элементу aA,
называется образом
этого элемента
a
. Множество всех образов элемента aA
будем обозначать δ(a,
G)
= {bbB,
(а,
b)G}.
Каждый
элемент aA,
соответствующий элементу bB,
называется прообразом
элемента b.
Множество всех прообразов элемента bB
будем обозначать δ─1(b,
G)
= {aaA,
(а,
b)G}.
Очевидно,
что множество всех образов всех элементов
aA
есть ни
что иное, как множество значений
соответствия G (его вторая проекция), а
множество всех прообразов всех элементов
bB
множество определения соответствия G
(его первая проекция).
Пусть
ХА,
а YB.
Образом
множества Х
при данном соответствии G
называется
такое множество
Г(X,G)
= {b
b=δ(x,G),
x
X,
b
B}.
Прообразом
множества Y
называется множество Г─1(Y,G)
= {x
x
A,
y
Y,
(x,
y)
G}.
Рассмотренное
выше соответствие относится к двум
множествам и поэтому носит название
бинарного
соответствия.
Однако этот понятие распространяется
на любое конечное число множеств.
Рассмотрим, например, декартово
произведение n
непустых
множеств: А1
А2
…Ап.
Рассмотрим какое-либо подмножество G
этого произведения, то есть отберём
элементы произведения, удовлетворяющие
некоторому условию
G
А1
А2
…Ап
=
=
{(a1,
a2,
…an)
a1A1,
a2A2,…,
anAn,
(a1,
a2,
…an)G}.
Это
подмножество называют п-местным
соответствием
на множестве А1
А2
…Ап.
Подобные многоместные соответствия
используются в теории баз данных.
Предметом же нашего рассмотрения будут
бинарные соответствия.
Задача
4.4.1.
Рассмотрим
экзаменационную ведомость студенческой
группы и установим соответствия между
студентами и полученными ими оценками.
Табл.4.1
|
Ф.И.О. студента |
Математика |
Физика |
История |
Физкультура |
|
Борисенко |
5 |
4 |
не |
2 |
|
Волошин |
2 |
не |
3 |
5 |
|
Марабу |
3 |
не |
3 |
5 |
|
Яковенко |
4 |
4 |
4 |
4 |
Решение.
Обозначим множество студентов через А
= {Б, В, М, Я},
множество оценок через B
= {2, 3, 4, 5}. Тогда соответствие G
AB
= {(Б,5), (Б,4), (Б,2), (В,2), (В,3), (В,5), (М,3), (М,5),
(Я,4), (Я,5)}. Некоторые упорядоченные пары
встречаются несколько раз, но мы их
записываем только один раз.
Первая
проекция (или область определения)
соответствия:
пр1G
= Dom(G)
= {Б,В,М,Я}, вторая проекция (область
значений):
пр2
= Im(G)
= {2,3,4,5}.
Образ
Б: δ(Б,G)
= {2,4,5}; образ В: δ(B,G)
= {2,3,5};
образ
M:
δ(M,G)
= {3,5}; образ Я:
δ(Я,G)
= {4}.
Прообраз
2: δ─1(2,G)
= {Б,В};
прообраз 3: δ─1(3,G)
= {В,М};
прообраз 4: δ─1(4,G)
= {Б,Я};
прообраз 5: δ─1(5,G)
= {Б,В,М}.
Задача
4.4.2. Дано
соответствие G
= {(a,2),
(b,1),
(b,5),
(d,4)}
для множеств А= {a,
b,
c,
d}
и B
= {1, 2, 3, 4, 5}. Найти образ множества X
= {a,
b}
и прообраз множества Y
= {3, 4}.
Решение.
Найдём образы элементов множества Х:
δ(а,G)=2;
δ(b,G)={1,5}.
Объединяя эти элементы в одно множество,
получим образ множества Х: Г(Х,G)
= {1,2,5}.
Найдём
прообразы элементов множества Y:
δ─1(3,G)
= ;
δ─1(4,G)
= d
. Поэтому
прообразом множества
Y
будет множество, состоящее из одного
элемента: Г─1(Y,G)
= {d}.
Пустое множество
является частью любого множества,
поэтому записи {,
d}
и { d
} выражают одну и ту же мысль.
Задача
4.4.3. Найти
образ отрезка [1, 10] при соответствии y
= lg
x.
Решение.
Функция
y
= lg
x
является
непрерывной и монотонной на множестве
(0, ∞) – множество А, область её изменения
(-∞, ∞) – множество В. G
= {(x,
y)|
xA,
yB,
y
= lg
x}.
Значению х=1
соответствует у
= lg1
= 0, значению х=10
соответствует у
= lg10
= 1. Следовательно, образом отрезка [1,
10] будет отрезок [0, 1].
Задачи для
самостоятельного решения.
1.
Дано соответствие G = {(a,4), (b,3), (b,2), (с,3),
(d,4)} для множеств А= {a, b, c, d} и B = {1, 2, 3, 4}.
Найти образы и прообразы элементов
множеств А и В, а также и прообраз множеств
X = {b, d} и Y = {2, 4}.
2.
Найти прообраз отрезка [-1, 1] при
соответствии y = sin x. (ответ – вся числовая
ось).
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Соответствия
Решение задач
- Дискретная математика
- Дискретная математика в примерах и задачах
- Соответствия
Соответствием g между множествами X и Y будем называть
тройку объектов: Г = (Х, K,G), где X — область отправления соответствия, Y — область прибытия соответствия, G — график соответствия, причём G ⊆ X × Y.
Областью определения соответствия будем называть пр1G.
Областью значений соответствия будем называть пр2G.
Соответствие называется всюду определённым, если пр1 G = X.
Соответствие называется сюръективным, если np2G = Y.
Соответствие будем называть функциональным, или функцией,
если его график не содержит пар с одинаковыми первыми и различными вторыми координатами.
Соответствие называется инъективным, если его график не
содержит пар с одинаковыми вторыми и различными первыми
координатами.
Соответствие называется отображением X в Y, если оно
всюду определено и функционально.
Соответствие называется отображением X на Y, если оно
всюду определено, функционально и сюръективно.
Соответствие называется взаимно однозначным, если оно
функционально и инъективно.
Соответствие называется биекцией, если оно всюду определено, сюръективно, функционально и инъективно.
Образом множества А при данном соответствии называется
множество Г(В) = {у|(х,у)∈ G и х∈ А].
Прообразом множecmвa В при данном соответствии называется множество Г-1 (В) = {х|(х,у)∈ G и у∈ В}.
Множества называются равномощными, если между ними
можно установить биекцию.
Множество называется счётным, если оно равномощно множеству натуральных чисел.
Множество называется континуальным, если оно равномощно множеству действительных чисел отрезка [0,1].
Задание 1.3.1
- Изобразить соответствие в виде графа.
- Выяснить, какими из 4 основных свойств (всюду определённость, сюръективность, функциональность, инъективность) обладает Г.
- Найти образ множества А и прообраз множества В при
данном соответствии. - Построить соответствие между бесконечными множествами, обладающее тем же набором свойств, что и Г.
- Построить соответствие между конечными множествами,
обладающее набором свойств, противоположным данному.
Замечание. Для данного и построенных соответствий отметить
случаи отображений, указать их тип, отметить случаи биекций.
Замечание. Для данного и постоенных соответствий отметить случаи отображений, указать их тип, отметить случаи биекций.
Таблица 1.3.1
| № | X | Y | G | A | B |
| 1 | a,b,с,d,e | 1,2,3 | (a,2),(b,3),(c,l),(d,2),(e,l) | e,c | 2,3 |
| 2 | a,b,с,d | 1,2,3,4 | (a,4),(b,3),(c,2),(d,1) | a,b | 1,3 |
| 3 | a,b,с,d | 1,2,3,4,5 | (a,3),(b,5),(c,4),(d,1) | a,c | 1,4 |
| 4 | a,b,с,d,e | 1,2,3,4 | (d,1),(b,2),(e,4),(a,3) | b,c | 1,2 |
| 5 | a,b,с,d,e | 1,2,3 | (b,2),(c,1),(e,3),(a,3) | e,c | 3,1 |
| 6 | a,b,с,d | 1,2,3,4 | (a,2),(b,3),(c,1),(a,4) | a,b | 1,2 |
| 7 | a,b,с,d,e | 1,2,3,4,5 | (a,5),(b,3),(d,1),(e,2) | d,e | 1,3 |
| 8 | a,b,с,d | 1,2,3,4 | (a,3),(b,4),(c,3),(d,1) | a,c | 1,3 |
| 9 | a,b,с | 1,2,3,4,5 | (a,2),(b,1),(c,5),(a,3) | a,b | 3,4 |
| 10 | a,b,с | 1,2,3 | (a,1),(a,3),(b,2),(c,3) | a,c | 2,3 |
| 11 | a,b,с,d | 1,2,3,4,5 | (a,2),(c,1),(d,5),(c,3) | b,c | 1,2 |
| 12 | a,b,с,d,e | 1,2,3,4 | (b,1),(c,3),(d,2),(c,1) | a,c | 1,2 |
| 13 | a,b,с,d | 1,2,3 | (a,1),(b,1),(c,3),(b,2) | b,d | 1,3 |
| 14 | a,b,с,d | 1,2,3,4 | (a,4),(b,3),(b,2),(c,3),(d,4) | a,b | 3,4 |
| 15 | a,b,с,d | 1,2,3,4 | (a,4),(c,4),(b,2),(a,3) | a,b | 2,4 |
| 16 | a,b,с,d,e | 1,2,3 | (a,2),(b,1),(d,3),(e,1) | a,b | 1,2 |
| 17 | a,b,с,d | 1,2,3,4 | (b,3),(a,2),(c,2),(d,1) | a,c | 1,4 |
| 18 | a,b,с,d | 1,2,3,4 | (a,3),(c,2),(d,1),(c,4) | c,d | 2,3 |
| 19 | a,b,с | 1,2,3,4,5 | (a,2),(b,5),(c,4),(b,3) | a,b | 2,5 |
| 20 | a,b,с,d | 1,2,3,4 | (a,1),(b,3),(a,2),(c,4) | a,b | 2,3 |
| 21 | a,b,с,d | 1,2,3,4 | (a,1),(b,3),(a,2),(c,4) | a,b | 2,3 |
| 22 | a,b,с,d | 1,2,3 | (a,1),(b,3),(c,2),(a,2) | a,b | 2,3 |
| 23 | a,b,с,d | 1,2,3,4 | (a,3),(b,4),(c,1),(d,2) | a,b | 1,4 |
| 24 | a,b,с | 1,2,3,4 | (a,3),(b,1),(c,2),(c,1) | a,c | 4,2 |
| 25 | a,b,с,d,e | 1,2,3 | (c,2),(d,1),(a,3),(b,3) | a,d | 3,1 |
| 26 | a,b,с,d | 1,2,3,4 | (b,2),(c,3),(d,1),(b,4) | b,c | 1,2 |
| 27 | a,b,с,d,e | 1,2,3,4,5 | (b,5),(c,3),(e,1),(a,2) | a,e | 1,3 |
| 28 | a,b,с,d | 1,2,3,4 | (b,3),(c,4),(d,3),(a,1) | b,d | 3,1 |
| 29 | a,b,с | 1,2,3,4,5 | (b,3),(c,4),(d,3),(a,1) | b,d | 3,1 |
| 30 | a,b,с | 1,2,3 | (b,1),(b,3),(c,2),(a,3) | a,b | 2,3 |
|
Пример решения заданя 1.3.1 Решим задание 1.3.1 для соответствия |
Рис 1.3.1,а |
- Изобразим соответствие в виде графа (рис. 1.3.1, а).
- Выясним, какими из свойств обладает данное соответствие.
α) Соответствие не всюду определено, так как
npjG -{a,byd} Ф X.
β) Соответствие не сюръективно, так как np2G = {1,2,4,5} Ф Y.
γ) Соответствие не функционально, так как его график содержит две пары (Ь,1)и (Ь,5) с одинаковыми первыми и различными вторыми координатами.
δ) Соответствие инъективно, так как его график G не содержит пар с одинаковыми вторыми и различными первыми координатами. - Найдём образ Г(А)и прообраз Г-1(В).
Г(А) = {1,2,5}, так как А = {a,b} и {(а,2),(b,1),(b,5)} ⊆ G
Г-1(B) = {d}, так как В = {3,4} и только (d,4) ⊆ G. -
Построим соответствие между бесконечными множествами,
обладающее тем же набором свойств, что и данное соответствие.
Пусть Х=[0,2], У = (-оо,+оо), G = {(x,y)x2 +у2=1 и х>0}.
Покажем, что это соответст-
вие (рис. 1.3.1, б) обладает тем же
набором свойств, что и данное.
|
α) Построенное соответствие β) Построенное соответствие γ) Построенное соответствие δ) Соответствие инъективно, так как его график не содержит |
Рис. 1.3.1, б
|
|
Построим соответствие между конечными множествами, чтобы оно было Г = ({u,v},{w},{(u,w),(v,w)}). Покажем, что это соответствие обладает требуемым набором свойств, |
Рис. 1.3.1, б |
α) Действительно, это соответствие всюду определено, так как
np1G = X = {u,v}.
β) Соответствие сюръективно, так как np2G = {w} = Y.
γ) Соответствие функционально, так как в его графике нет
пар с одинаковыми первыми и различными вторыми координатами.
δ) Соответствие не инъективно, так как его график состоит из
двух пар (u,w)и , (v,w) с различными первыми и одинаковыми
вторыми координатами.
Так как построенное соответствие всюду определено,
сюръективно и функционально, оно является отображением X
на Y.
Задание 1.3.2
Для соответствия Г =(X,Y,G)
- Определить набор свойств, которыми обладает данное соответствие.
- Построить соответствие между конечными множествами
с набором свойств, противоположным данному, изобразив соответствие аналитически и в виде графа.
Замечание. Отметить случаи отображений и биекций.
Таблица 1.3.2
| № | X | Y | G |
| 1 | многочлены 2 степени от одной переменной с действительными коэффичентами | R | (многочлен, его корень) |
| 2 | множество кугов на плоскости | множество точек плоскости | (круг, его центр) |
| 3 | (0, + ∞) | [-1,1] | (x,y)|x2 |
| 4 | N | R | (x, ± 1n x) |
| 5 | R | непрерывные на [a,b] функции |

|
| 6 | вузы вашего города | жители вышего города | (вуз; человек, окончивший этот вуз) |
| 7 | (0, + ∞) | отрезки на прямой | (x, отрезок длины x) |
| 8 | фамилии студентов вашей группы | {1,2,…,100} | (фамилия, число букв в фамилии) |
| 9 | окружности на плоскости | Z | (окружность, ее длина) |
| 10 | функции, определенные на [0,1] | R | (функция, ордината ее точки максимума) |
| 11 | R2 | N |

|
| 12 | Имена студентов вашей группы | буквы русского алфавита | (имя, буква из имени) |
| 13 | N | студенты вашего вуза | (n, человек с годом рождения n) |
| 14 | [0,1] | {0,1} |
(x,f(x)), где
|
| 15 | R | R10 |
(maxai,(at,a2,..,a10)) 1≤i≤10 |
| 16 | окружности на плоскости | прямые на плоскости | (окружность, касательная к этой оружности) |
| 17 | [P(U)]3 | P(U) | ((A,B,C),A⌒B⌒C) |
| 18 | [0,1] | R2 | (x,(x,y)|x2+ y2 = 1) |
| 19 | R | функции, непрерывные на [0,1] |

|
| 20 | P(U) | [P(U)]3 |

|
| 21 | {0,1,2} | N | (x,y)|x — остаток от деления y на 3 |
| 22 | [1,3] | R+ | (x,y)|(x-2)2 + (y-2)2≤1 |
| 23 | пары окружностей на плоскости | R2 | (пара окружностей, координаты точки пересечения этих окружностей) |
| 24 | множество книг в библиотеке вашего вуза | Z | (книга, число страниц в этой книге) |
| 25 | (-4,4) | [1,6] | (x,y)|y=|x-2|+1 |
| 26 | мужчины вашего города | женщины вашего города | (x,y)|x и y состоят или когда-либо состояли друг с другом в законном браке |
| 27 | [P(U)]2 | P(U) | ((A,B),AB) |
| 28 | политические партии вашего города | жители вашего города | ((партия), (человек, состоящий в этой партии) |
| 29 | P(U), где U ={1,2,…,40} | N | (A,|A|), где A∈ P(U) |
| 30 | пары прямых на плоскости | R | (пара прямых, абцисса точки пересечения прямых) |
Пример решения задания 1.3.2
Решим задание 1.3.2 для соответствия Г = (X,Y,G), если
X = N, Y — множество непрерывных на [а,Ь] функций, а график G задан так: G =
1. Определим набор свойств, которым обладает данное соответствие.
α) Для любого натурального числа п можно рассмотреть непрерывную функцию f(x) =
будем иметь:
Итак, доказано, что данное соответствие является всюду определённым.
β) Так как для некоторых непрерывных функций на [а,b] определённый интеграл не выражается натуральным числом, то
данное соответствие не является сюръективным.
γ) Покажем, что две различные функции могут иметь на рассматриваемом промежутке одинаковое значение определённого
интеграла. Для этого можно рассмотреть функции
Для f(x) определённый интеграл не отрезке [а,b], как мы
уже выяснили, равен n. Найдём соответствующий интеграл
для g(x):
Итак, доказано, что соответствие, описанное в условии задания, не является функциональным.
δ) Так как для каждой функции её определённый интеграл на
данном промежутке находится однозначно, данное соответствие
является инъективным.
2. Построим соответствие между конечными множествами,
чтобы оно было не всюду определено, сюръективно, функционально и не инъективно.
|
Пусть Г = ({a,d,c},{1},{(а,1),(b,1)} |
Рис. 1.3.2 |
α) Соответствие Г не всюду определено, так как элемент с, входящий в область отправления, не имеет образа при
данном соответствии.
β) Соответствие Г сюръективно, так как его область прибытия {1} совпадает с областью значений.
γ) Соответствие Г функционально, так как его график не содержит пар с равными первыми и различными вторыми координатами.
δ) Соответствие Г не инъективно. так как в его графике пары
(а,1) и (b,1) имеют различные первые и одинаковые вторые координаты.
Задание 1.3.3
Установить биекцию между множествами
Таблица 1.3.3
| № | Множества |
| 1 |
{(x,y)|x2+y2≤1}и{(x,y)|x2+y2<1} |
| 2 |
[0,1] и R |
| 3 |
[0,+∞)и[0,1] |
| 4 |
N и множество многочленов 3й степени с натуральными коэффицентами |
| 5 |
R и [0,+∞] |
| 6 |
{(x,y)|x2+y2=1} и [0.1) |
| 7 |
все окружности на плоскости и R×R×(0,+∞) |
| 8 |
{(x,y)|-π2 < x < π2 ,0 < y < π} и R2 |
| 9 |
Q⌒[0,1] и Q2⌒[0,1]2 |
| 10 |
(0,1) и [e,π] |
| 11 |
[0,+∞) и (a,b) |
| 12 |
все интервалы на прямой и полуплоскость, расположенная ниже линии y=x |
| 13 |
{(x,y)|x2+y2≤1} и {(x,y)|x2+y2<100} |
| 14 |
Q и Q⌒[0+∞) |
| 15 |
[0,1] и (2,5) |
| 16 |
полуокружность без концевых точек и луч (0,+∞) |
| 17 |
(-∞,0) и R |
| 18 |
N и Q2 |
| 19 |
Q и множество всех многочленов с рациональными коэффицентами |
| 20 |
(0,1) и R |
| 21 |
Q и Q2 |
| 22 |
сфера с выколотой точкой и вся плоскость |
| 23 |
{(x,y)|x2+y2≤4} и {(x,y)|x2+y2≥4} |
| 24 |
Q и Q⌒[0,1] |
| 25 |
R и [1,+∞)∪{-10} |
| 26 |
N и N2 |
| 27 |
все последовательности натуральных чисел и все возрастающие последовательности натуральных чисел |
| 28 |
N и множество всех многочленов с натуральными коффицентами |
| 29 |
R и RQ |
| 30 |
Q и N2 |
Пример решения задания 1.3.3
Установить биекцию между множествами [0,1] и (0,1).
Будем считать, что Х=[0,1], К = (0,1).Пусть A={ 1/2 , 1/3 ,…, 1/n ,…}, B={ 0,1, 1/2 , 1/3 ,…, 1/n ,…}=A∪{0,1}
Очевидно, что XB=YA, X=XB∪B, Y=YA∪A.
Установим биекцию между множествами ХВ и УА, как
тождественное соответствие f(x) = х.
Биекцию между множествами А и В зададим так:
f(0)=1/2 , f(1)=1/3 , f(1/2) = 1/4 , f(1/3) = 1/5 ,…,f(1/n)= 1/n+2 ,…
Таким образом, между X и К установлена биекция:
Изобразим график этой биекции в декартовой системе координат (рис. 1.3.3).
Рис. 1.3.3
Задание выполнено
Задание 1.3.4
Доказать, что множество:
Таблица 1.3.4
| № |
Условие |
| 1 |
всех многочленов от х с рациональными коэффициентами счетно |
| 2 |
всех пар рациональных чисел счётно |
| 3 |
всех многочленов от дг с целыми коэффициентами счётно |
| 4 |
всех кругов на плоскости, радиусы которых и координаты центра |
| 5 |
попарно непересекающихся замкнутых кругов на плоскости не более |
| 6 |
всех многочленов n-й степени от х с рациональными коэффициентами счётно |
| 7 |
всех многочленов п -и степени от х с целыми коэффициентами счётно |
| 8 |
попарно непересекающихся прямоугольников на плоскости не более |
| 9 |
всех окружностей на плоскости, радиусы которых и координаты центра являются целыми числами — счётно |
| 10 |
полученное объединением счётного числа конечных множеств — не |
| 11 |
полученное объединением счётного числа счётных множеств — |
| 12 |
рациональных чисел интервала (0,1) — счётно |
| 13 |
непересекающихся окружностей на плоскости может быть континуально |
| 14 |
всех действительных чисел интервала (0,1), в десятичном разложении |
| 15 |
точек разрыва монотонно убывающей на [а,Ь] функции — не более |
| 16 |
точек плоскости, расстояние между любыми элементами которого |
| 17 |
попарно непересекающихся открытых интервалов на прямой не более |
| 18 |
полученное объединением счётного числа непустых попарно непересекающихся конечных множеств, счётно |
| 19 |
всех конечных последовательностей натуральных чисел — счётно |
| 20 |
всех конечных подмножеств счётного множества — счётно |
| 21 |
попарно непересекающихся букв Г на плоскости может быть континуально |
| 22 |
попарно непересекающихся букв L на плоскости может быть континуально |
| 23 |
попарно непересекающихся букв Т на плоскости не более чем счётно |
| 24 |
А1×А2×…×Аn— счётно, если каждое из множеств А1,А2,…,Аn — |
| 25 |
чисел вида 2n .3m —счётно, если не N и m∈ N |
| 26 |
иррациональных чисел интервала (0,1) — несчётно |
| 27 |
всех бесконечных последовательностей, составленных из нулей и |
| 28 |
всех корней многочленов третьей степени с натуральными коэффициентами — счётно |
| 29 |
функций вида f:E»->E, где E = {0,1}, п = 1,2,3,… — счётно |
| 30 |
полученное объединением конечного числа счётных множеств — счётно |
Пример решения задания 1.3.4
Доказать, что множество всех конечных последовательнос-
тей, составленных из элементов некоторого счётного мно-
жества, счётно.
Пусть множество А счётно, А = {а1,а2,…,an,…}. Обозначим
через Вк множество конечных последовательностей длины к,
составленных из элементов множества A, k∈N. Покажем для
любого к, что множество Вк —счётно.
Пусть
Таким образом, любая конечная последовательность длины k,
составленная из элементов счётного множества, получит свой номер.
Выпишем элементы множеств Вk в виде бесконечной таблицы, где k∈N.
|
Таблица 1.3.4 |
Будем обходить таблицу по |
Имеем, что для любых индексов i,p последовательность bpi
получит когда-нибудь единственный номер.
Таким образом, установлена биекция между множеством, составленным из элементов bpi, и множеством индексов N,
то есть доказана счётность множества всех конечных последовательностей, составленных из элементов некоторого счётного
множества А.
Соответствия и бинарные отношения на множествах
Отображение из множества
в множество
считается заданным, если каждому элементу
сопоставлен единственный элемент
. Отображение
из множества
в множество
обозначают записью
или
. Элемент
, который отображением
сопоставляется элементу
, называют образом элемента
при отображении
и обозначают
.
Каждое отображение однозначно определяет множество упорядоченных пар , являющееся подмножеством декартова произведения
множества
на множество
и называемое графиком отображения
.
Наоборот, пусть в декартовом произведении задано такое подмножество
, что:
1) для любого существует
, для которого
;
2) для любых двух пар и
множества
из равенства
следует равенство
.
Тогда множество единственным образом определяет некоторое отображение из
в
. Это отображение, обозначаемое также
, элементу
сопоставляет элемент
, удовлетворяющий условию
. Таким образом, мы можем отождествить отображения с их графиками и считать, что отображение есть подмножество декартова произведения.
Отображение множества
в себя называют тождественным, если
при всех
из
.
В общем случае для отображения может существовать несколько различных элементов множества
, образы которых совпадают. Множество всех элементов
, для которых
, называют прообразом элемента
при отображении
.
Так, прообраз числа при отображении
есть множество всех решений уравнения
, т.е. множество
Прообраз элемента может быть пустым множеством. Это имеет место, например, для числа
при отображении
.
Множество всех , таких, что найдется
, для которого
, называют областью значений отображения
. Область значений отображения
будем обозначать
.
Отображение называют инъективным (инъекцией), если каждый элемент из области его значений имеет единственный прообраз, т.е. из
следует
.
Отображение называют сюръективным (сюръекцией), если его область значений совпадает со всем множеством
. Сюръективное отображение из
в
называют также отображением множества
на множество
.
Отображение называют биективным (биекцией), если оно одновременно инъективно и сюръективно.
Таким образом, если отображение биективно, то каждому элементу множества
отвечает единственный элемент множества
и наоборот. Тогда говорят, что множества
и
находятся между собой во взаимно однозначном соответствии.
Биекцию множества на себя называют автоморфизмом множества
. Используют также термин «подстановка множества».
Пример 1.2. а. Отображение, заданное равенством , есть, как нетрудно показать, биекция множества натуральных чисел
на его подмножество
.
б. Отображение есть биекция множества всех натуральных чисел на множество всех четных натуральных чисел.
в. Любая показательная функция , есть биекция множества
всех действительных чисел на множество
всех положительных действительных чисел.
г. Функция есть биекция множества
на интервал
.
д. Поворот окружности на заданный угол , т.е. отображение, сопоставляющее каждой точке окружности точку, в которую она перейдет при повороте всей окружности вокруг ее центра на угол
, есть автоморфизм множества точек окружности.
Образ и прообраз множества
Пусть задано отображение и
— некоторое множество. Множество
элементов
, таких, что
, называют образом множества
при отображении
. Например, при отображении
отрезок
является образом множества (отрезка)
, равно как и любого объединения отрезков вида
(для произвольного целого
). При
это можно записать следующим образом:
.
Заметим, что для любого отображения образ
всего множества
есть область значений данного отображения.
Для произвольного множества множество всех элементов
, таких, что
, называют прообразом множества
при отображении
.
Например, для любого действительного числа множество, которое является объединением всех отрезков вида
есть прообраз отрезка при отображении
.
Прообраз области значений произвольного отображения совпадает со всем множеством
.
Множество всех отображений из в
будем обозначать как
.
Частичное отображение и его область определения
Понятие отображения можно обобщить. Обобщение может проходить по двум позициям. Во-первых, можно отказаться от полной определенности отображения, полагая, что образ определен не для каждого элемента множества , а для некоторых элементов этого множества. Тогда придем к понятию частичного отображения. При этом подмножество всех элементов
, для которых определен образ, называют областью определения данного частичного отображения.
Многие элементарные функции являются частичными отображениями множества всех действительных чисел в себя. Например, функция
есть частичное отображение с областью определения
Во-вторых, можно отказаться от однозначности отображения, полагая, что данному сопоставлен не один, а несколько образов (множество образов) в множестве
. В этом случае говорят, что задано соответствие из множества
в множество
.
Примером могут служить обратные тригонометрические функции: скажем, «большой» арксинус, сопоставляющий каждому множество всех таких чисел
, что
, т.е. множество, являющееся прообразом элемента
при отображении, определяемом графиком функции
.
Если задано соответствие из
в
, будем использовать обозначение
по аналогии с обозначением
для отображений, понимая при этом, что
есть уже не элемент множества
, а его подмножество.
Аналогично графику отображения можно определить график соответствия из множества
в множество
как множество
упорядоченных пар
, таких, что
и элементы
связаны соответствием
, то есть
. Указанное множество
упорядоченных пар есть подмножество декартова произведения
.
Обратно, фиксируя на декартовом произведении какое-либо подмножество
, мы тем самым однозначно определяем некоторое соответствие
из
в
, а именно
Нетрудно заметить, что графиком соответствия будет как раз множество
, а соответствием, отвечающим графику
, будет
. Поэтому можно отождествить соответствие с его графиком и считать, что соответствие из множества
в множество
есть некоторое подмножество
декартова произведения
, то есть
. В частности, при
получаем пустое соответствие, а при
, совпадающем со всем указанным декартовым произведением, — универсальное соответствие.
При этом будем писать для упорядоченных пар, связанных соответствием
.
Используют также термины «частичное мультиотображение» и «частичная многозначная функция».
Пример 1.3. Рассмотрим множество программистов и множество программ
. Зададим соответствие
из
в
, связывающее программистов и разрабатываемые ими программы:
Область определения соответствия из множества
в множество
— это множество всех первых компонент упорядоченных пар из
Область значения соответствия — это множество всех вторых компонент упорядоченных пар из
Из определения вытекает, что . Соответствие из
в
называют всюду определенным, если его область определения совпадает с множеством
.
Сечением соответствия для фиксированного элемента
будем называть множество
. Можно сказать, что сечение соответствия
есть множество всех «образов» элемента
при данном соответствии.
Сечением соответствия по множеству
будем называть множество
Пример 1.4. Область определения соответствия т из примера 1.3 есть все множество , а область значения — все множество
. Сечением соответствия
по элементу
будет множество
.
Бинарные отношения на множествах
Соответствие из множества
в себя, т.е. подмножество множества
, называют бинарным отношением на множестве
.
Пример 1.5. Простейшим примером бинарного отношения является отношение нестрогого неравенства на множестве действительных чисел . Здесь каждому
поставлены в соответствие такие
, для которых справедливо
.
Для произвольного бинарного отношения на некотором множестве часто используют запись вместо
, говоря при этом об элементах, связанных бинарным отношением
. Это согласуется с традиционной формой записи некоторых часто используемых бинарных отношений. Так, пишут
, а не
. Для таких бинарных отношений употребляют устоявшиеся словосочетания. Например, запись
читается так: «
не больше
«.
Бинарное отношение на множестве , состоящее из всех пар
, т.е. пар с совпадающими компонентами, называют диагональю множества
и обозначают
. Нетрудно понять, что диагональ
есть тождественное отображение
на себя.
Иногда говорят о диагонали в множестве , хотя правильнее было бы называть это отношение диагональю декартова квадрата множества
.
Для наглядного изображения соответствий из в
(бинарных отношений, в частности) будем использовать два способа. Первый из этих способов состоит в интерпретации соответствия как подмножества декартова произведения, которое можно изображать примерно так же, как на плоскости можно изображать подмножества декартова квадрата числовых множеств. Второй способ, применяемый для конечных множеств
в
, — построение так называемого графа соответствия. В этом случае элементы множеств
в
изображаются на плоскости кружочками. Если и только если пара
принадлежит соответствию
, то в графе соответствия из кружочка, обозначающего элемент
, проводим стрелку к кружочку, обозначающему элемент
. Для бинарного отношения на конечном множестве
часто удобнее использовать граф другого вида. Элементы множества
изображаются кружочками только один раз, а стрелки проводятся по тем же правилам, что и в графе соответствия. Заметим, что при таком построении возможно соединение кружочка стрелкой с самим собой (петля).
Пример 1.6. а. На рис. 1.1, а изображены график и граф бинарного соответствия из примера 1.3.
б. Пусть . Бинарное отношение
на
определим как множество всех упорядоченных пар
, таких, что
. Тогда
Область определения отношения , область значений
. График и два варианта графа отношения
изображены на рис. 1.1, б.
в. Множество точек окружности есть график бинарного отношения на множестве действительных чисел, состоящего из всех таких упорядоченных пар
, что
, или, что равносильно, компоненты пары удовлетворяют уравнению
. Область определения бинарного отношения есть отрезок
, область значения — также отрезок
.
Функциональное соответствие
Соответствие называют функциональным по второй (первой) компоненте, если для любых двух упорядоченных пар
и
из равенства
следует
(и из
следует
). Функциональность соответствия по второй компоненте означает, что, фиксируя в любой упорядоченной паре, принадлежащей данному соответствию, первую компоненту, мы однозначно определяем и вторую компоненту. Таким образом, мы можем сказать, что соответствие, функциональное по второй компоненте, есть отображение (возможно, частичное).
Поэтому соответствие является отображением из
в
, если и только если оно всюду определено (т.е.
) и функционально по второй компоненте. Отметим также, что отображение из
в
является инъекцией тогда и только тогда, когда оно функционально по первой компоненте.
Отношения произвольной арности
В заключение обобщим понятие соответствия, определив отношения произвольной арности.
Определение 1.4. Произвольное подмножество декартова произведения
называют (п-арным или п-местным) отношением на множествах
.
В случае если все множества совпадают, т.е.
, говорят об n-арном отношении на множестве
.
Если — n-арное отношение на множествах
и
, то говорят об элементах
, связанных отношением
.
Замечание 1.3. При получаем бинарное отношение на множествах
. Это не что иное, как соответствие из
в
, где множества
и
, вообще говоря, различны.
При получаем введенное ранее бинарное отношение на множестве, т.е. подмножество декартова квадрата
.
Таким образом, в общем случае (при произвольном ) следует, строго говоря, различать термины «n-арное отношение» и «n-арное отношение на множестве».
Связь между введенными понятиями отношения, соответствия и отображения проиллюстрирована на рис. 1.2.
Пусть n-арное отношение удовлетворяет условию: для любых двух кортежей
и
из выполнения равенств для любого
следует, что и
. Тогда отношение
называют функциональным по i-й компоненте
.
Другими словами, функциональность n-местного отношения по i-й компоненте равносильна условию, что, фиксируя все компоненты, кроме i-й, мы однозначно определяем и i-ю компоненту.
Пример 1.7. а. Представим строку учебного расписания как кортеж вида
(преподаватель, группа, дисциплина, аудитория, день, час).
Тогда расписание можно рассматривать как секстарное (шестиместное) отношение на соответствующих множествах. Оно будет функционально по первой компоненте, если, конечно, предположить, что два преподавателя или более не проводят одно и то же занятие одновременно в одном и том же месте (хотя, например, на лабораторных работах это возможно). Оно также функционально по третьей компоненте (один преподаватель не может вести одновременно занятия по разным дисциплинам), по четвертой (преподаватель со своей группой не могут находиться в разных аудиториях) и не будет, вообще говоря, функционально по второй, пятой и шестой компонентам.
б. Рассмотрим на множестве геометрических векторов в пространстве тернарное (трехместное) отношение
, состоящее из всех упорядоченных троек
компланарных векторов. Это отношение не является функциональным ни по одной компоненте, так как любым двум векторам соответствует бесконечно много векторов, образующих с ними компланарную тройку.
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
ЛЕКЦИЯ 12 Образ и прообраз множества при данном соответствии 21. 11. 2012 г.
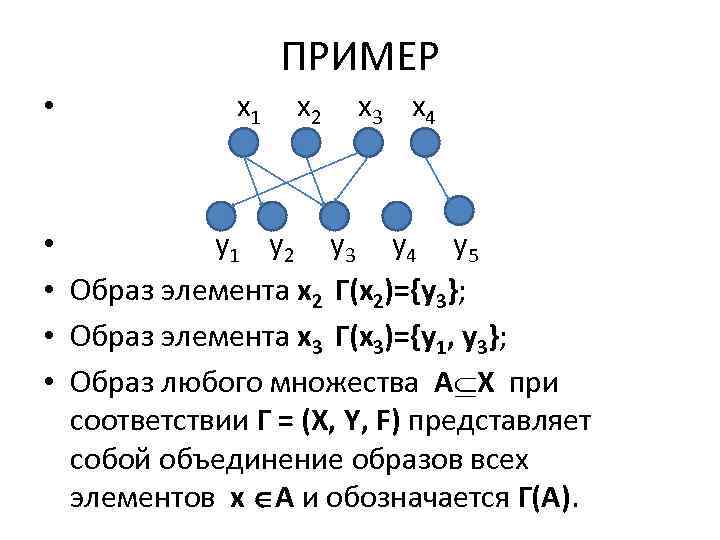
• Пусть дано соответствие Г = (X, Y, F). • Образом элемента х Х при соответствии Г называется и через Г(х) обозначается множество элементов y Y, для которых пара F. Иначе, Г(х)={y Y| F}. Т. е. , образ элемента х Х – это множество тех элементов y Y, которые соответствуют элементу x. • На графе образ элемента x можно представить как множество тех вершин y, в которые входят дуги, выходящие из вершины x.
ПРИМЕР • x 1 x 2 x 3 x 4 • y 1 y 2 y 3 y 4 y 5 • Образ элемента x 2 Г(x 2)={y 3}; • Образ элемента x 3 Г(x 3)={y 1, y 3}; • Образ любого множества A X при соответствии Г = (X, Y, F) представляет собой объединение образов всех элементов x A и обозначается Г(А).
• В общем случае справедливо: • Г(А) = Г(х) • х А • Для рассмотренного примера если А={x 2, x 3}, то Г(А)=Г(х2) Г(х3)={y 3} {y 1, y 3}={y 1, y 3}. • Пусть дано соответствие Г = (X, Y, F). • Прообразом элемента y Y при соответствии Г называется и через Г-1(y) обозначается множество элементов x X, для которых пара F.
5 • Таким образом, Г-1(y)={x X| F } – это множество тех элементов из Х, которым соответствует элемент y. • На графе прообраз элемента y можно представить множеством тех вершин х, из которых выходят дуги, заходящие в вершину y. Для рассмотренного примера • Г-1(y 3)={x 1, x 2, x 3}, Г(y 4)= .
6 • Прообразом произвольного множества B Y при соответствии Г = (X, Y, F) называется объединение прообразов всех элементов y B и обозначается Г-1(В), т. е. • Г-1(В) = Г-1(y) • y B • Если В={y 3, y 4, y 5}, то при соответствии Г для рассмотренного примера прообраз запишется • Г-1(В)={x 1, x 2, x 3, x 4}.
7 • Пусть Г = (X, Y, F) – произвольное соответствие и А – произвольное подмножество множества Х. • Сужением соответствия Г на множество А называется и через ГА обозначается соответствие, график которого FA определяется выражением: • FA = (A Y) F, т. е. ГА = (X, Y, FA). • Соответствие ГА Г. Соответствие Г в этом случае называют продолжением соответствия ГА на множество Х.
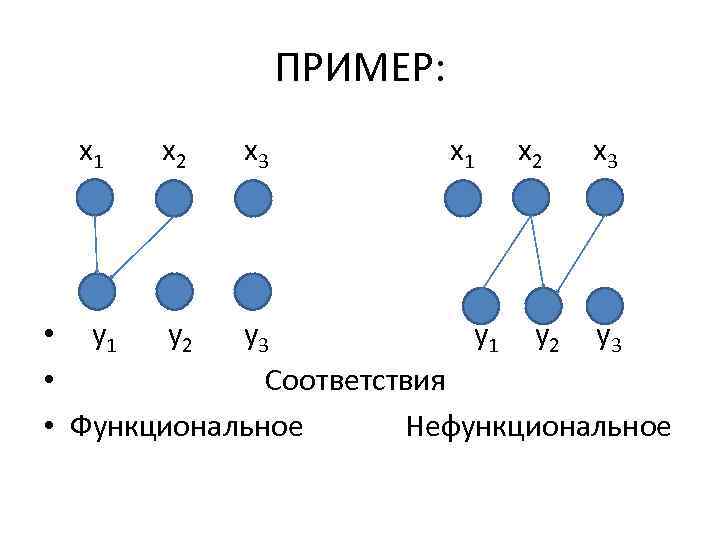
Основные свойства соответствий • 1. ФУНКЦИОНАЛЬНОСТЬ: • Соответствие Г = (X, Y, F) называется функциональным, если для любого х Х образ Г(х) содержит не более одного элемента y Y, в противном случае соответствие называется нефункциональным.
ПРИМЕР: x 1 x 2 x 3 • y 1 y 2 y 3 • Соответствия • Функциональное Нефункциональное
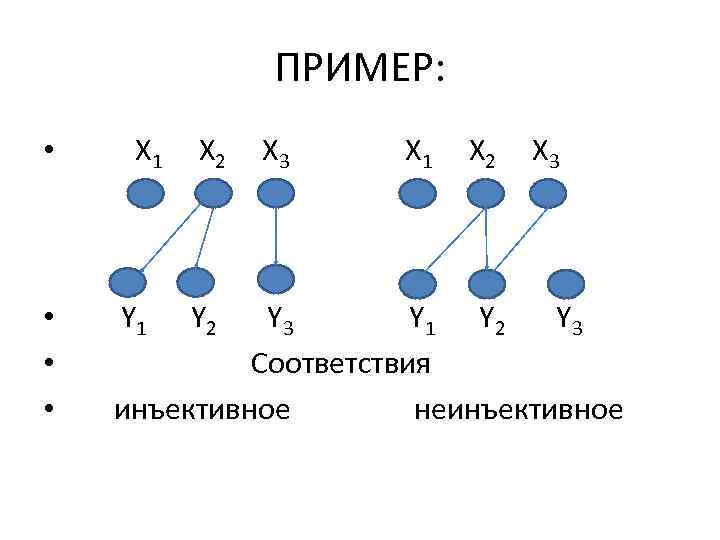
10 • 2. ИНЪЕКТИВНОСТЬ: • Соответствие Г = (X, Y, F) называется инъективным, если для любого y Y прообраз Г-1(y) содержит не более одного элемента х Х, в противном случае соответствие называется неинъективным.
ПРИМЕР: • • X 1 Y 1 X 2 Y 2 X 3 X 1 X 2 X 3 Y 1 Y 2 Y 3 Соответствия инъективное неинъективное
12 • 3. ОПРЕДЕЛЕННОСТЬ: • Соответствие Г = (X, Y, F) называется всюду определенным, если для каждого х Х образ Г(х) , в противном случае соответствие не всюду определено. • В графе всюду определенного соответствия из каждой вершины х Х выходит хотя бы одна дуга.
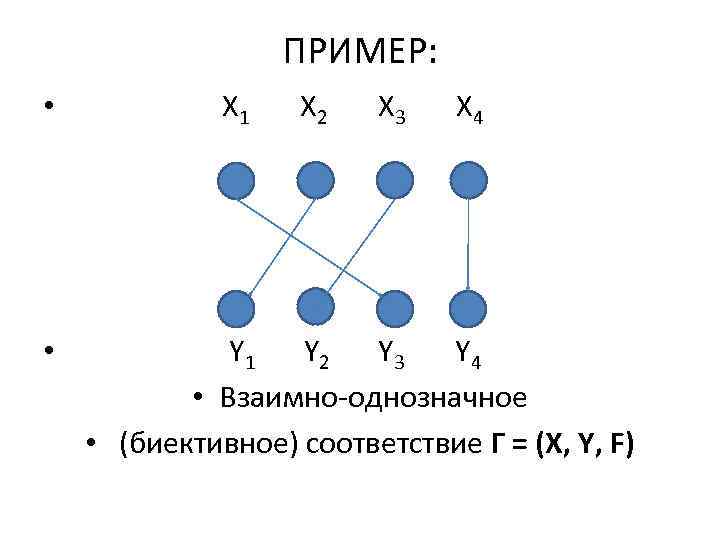
13 • 4. СЮРЪЕКТИВНОСТЬ: • Соответствие Г = (X, Y, F) называется сюръективным, если для любого элемента y Y прообраз Г-1(y) , в противном случае соответствие несюръективно. • В графе сюръективного соответствия в каждую вершину, соответствующую y Y, входит хотя бы одно ребро (дуга, стрелка). • Если соответствие одновременно функциональное, инъективное, всюду определенное и сюръективное, то оно называется взаимно-однозначным или биективным.
ПРИМЕР: • • X 1 X 2 X 3 X 4 Y 1 Y 2 Y 3 Y 4 • Взаимно-однозначное • (биективное) соответствие Г = (X, Y, F)
14 • Биекция — это отображение, которое является одновременно и сюръективным, и инъективным. При биективном отображении каждому элементу одного множества соответствует ровно один элемент другого множества, при этом, определено обратное отображение, которое обладает тем же свойством. Поэтому биективное отображение называют ещё взаимно-однозначным отображением (соответствием), одно-однозначным отображением. • Если между двумя множествами можно установить взаимно-однозначное соответствие (биекция), то такие множества называются равномощными. С точки зрения теории множеств, равномощные множества неразличимы. • Взаимно-однозначное отображение конечного множества в себя называется перестановкой (элементов этого множества). (википедия)
Общее понятие функции • Пусть Х – некоторое числовое множество. • Говорят, что на Х задана функция, если любому элементу из множества Х поставлено в соответствие определенное число y Y. • Если теперь перейти от числовых множеств к множествам произвольной природы, то приходим к самому общему понятию ФУНКЦИИ.
17 • Пусть X и Y – множества произвольной природы, и пусть между ними задано соответствие. • Если соответствие функционально, то оно называется функцией и обозначается • f = (X, Y, F). • Из определения следует, что функция может быть определена не на всех элементах множества Х.
18 • Если же функция определена на всех элементах множества Х, т. е. введенное соответствие не только функциональное, но и всюду определенное, то такая функция называется ОТОБРАЖЕНИЕМ. • Различают отображение X на Y и отображение X в Y. • X на Y, если f(X) = Y, • X в Y, если f(X) Y. • ФУНКЦИЯ – частный вид СООТВЕТСТВИЯ.
Скачать материал

Скачать материал


- Сейчас обучается 39 человек из 27 регионов




- Сейчас обучается 358 человек из 65 регионов


Описание презентации по отдельным слайдам:
-
1 слайд
ОП.08. Дискретная математика
Соответствия
для специальности 09.02.01 «Компьютерные системы и комплексы» -
2 слайд
Соответствие. Свойства соответствий.
2 -
3 слайд
Основные определения
Область определения соответствия G – множество пр1G={a: (a,b)G}
Область значений соответствия G – множество пр2G={b: (a,b)G}
3 -
4 слайд
Основные определения
Пример 1. Экзаменационная ведомость устанавливает следующее соответствие :
А={Иванов, Петров, Сидоров, Конев, Синицын, Васечкин, Макарова}.
В={2, 3, 4, 5}.
Иванов – 4
Петров – 2
Сидоров – 3
Конев – 4
Синицын на экзамен не явился
Васечкин – 3
Макарова – 5
G АВ, G-соответствие между студентами и оценками
4 -
5 слайд
G={(Иванов, 4), (Петров, 2), (Сидоров, 3), (Конев, 4), (Васечкин, 3), (Макарова, 5)}.
Область определения соответствия G –
пр1G={Иванов, Петров, Сидоров, Конев, Васечкин, Макарова}.
Область значений соответствия G – пр2G={2, 3, 4, 5}.Основные определения
А={Иванов, Петров, Сидоров, Конев, Синицын, Васечкин, Макарова}.
В={2, 3, 4, 5}.
5 -
6 слайд
Основные определения
В примере 1:
образом Иванова является 4;
образом Сидорова — 3 и т.д.
Прообразом 2 является Петров;
Прообразом 4 – Иванов, Конев.
6 -
7 слайд
Свойства соответствий
Соответствие GАВ называется всюду (полностью) определенным, если область определения совпадает с множеством А, т.е. пр1G=А. В противном случае соответствие называется частично определенным.
Соответствие GАВ называется сюръективным, если область значений совпадает с множеством В, т.е. пр2G=В.
Соответствие GАВ называется функциональным, если образом любого элемента а из области определения пр1G является единственный элемент b из области значений пр2G.
Соответствие GАВ называется инъективным, если прообразом любого элемента b из области значений пр2G является единственный элемент а из области определения пр1G.
7 -
8 слайд
Свойства соответствий
Определим свойства соответствия в примере 1.Частично определено, так как нет образа для Синицына;
Сюръективно, так как для каждой оценки определен прообраз;
Функционально, так как каждому студенту соответствует единственная оценка;
Неинъективно, так как оценка 4 соответствует двум студентам.
G={(Иванов, 4), (Петров, 2), (Сидоров, 3), (Конев, 4), (Васечкин, 3), (Макарова, 5)}.
А={Иванов, Петров, Сидоров, Конев, Синицын, Васечкин, Макарова}.
В={2, 3, 4, 5}.
пр1G={Иванов, Петров, Сидоров, Конев, Васечкин, Макарова}.
пр2G={2, 3, 4, 5}.
8 -
9 слайд
Свойства соответствий
частично определено, несюръективно, функционально, инъективноЧастично определено, сюръективно, нефункционально, инъективно
9 -
10 слайд
Свойства соответствий
Всюду определено, несюръективно, функционально, инъективно
Всюду определено, сюръективно, функционально, неинъективно
Всюду определено, сюръективно, функционально, инъективно
10 -
11 слайд
Свойства соответствий
11 -
-
13 слайд
GR+R+
Найти образы и прообразы чисел: 0, 1, 2; отрезков: [0,1], [2,3]
13 -
14 слайд
Пример 3. Соответствие G R R+ задано графиком. Найти образы и прообразы чисел: 0, 2, 3; отрезков [0,2], [-1,2]. Определить свойства соответствия.
14 -
15 слайд
Домашняя работа: определите свойства соответствий.
Придумайте пример соответствия, которое обладает свойствами: всюдоопределено, несюръективно, нефункционально, инъективно
3
Свойства соответствий
15 -
16 слайд
Функции. Отображения. Типы отображений
Взаимнооднозначные соответствия16
-
17 слайд
Функции и отображения
Функциональное соответствие называется функцией.
Если функция f устанавливает соответствие между множествами А и В, то говорят, что функция имеет тип АВ (обозначается f : АВ).
Каждому элементу а из области определения функция f ставит в соответствие элемент b из области значений. Это обозначается f(а)=b. Элемент а называется аргументом функции, элемент b – значение функции на а.
17 -
18 слайд
Функции и отображения
Отображением А в В называется всюду определенная функция f : АВ (обозначается f : А В).
Отображением А на В называется всюду определенная и сюръективная функция f : АВ (обозначается f : А В).
18 -
19 слайд
Какое соответствие является функцией, отображением в, отображением на?
19
Функции и отображения -
20 слайд
Функции и отображения
тип
Как нужно определить эту функцию, чтобы она стала отображением N на N
20 -
21 слайд
Взаимно-однозначное соответствие
Соответствие называется взаимно-однозначным, если оно всюду определено, сюръективно, функционально и инъективно.
A
B
C
D
K
X
a
b
c
d
r
Y
G X Y
Взаимно-однозначное соответствие
+
+
+
+
инъективное
21 -
22 слайд
Какое соответствие является взаимно-однозначным?
𝑓: 𝑋 в 𝑌
𝑓: 𝑋 на 𝑌
22
Взаимно-однозначное соответствие -
23 слайд
Взаимно-однозначное соответствие
23 -
24 слайд
Мощность множеств
Понятие мощности возникает при сравнении множеств по числу элементов.
Мощностью конечного множества является число его элементов. Множество, не являющееся конечным, называется бесконечным.
Если между множествами А и В существует взаимно-однозначное соответствие, то мощности этих множеств равны, т.е. А=В. В таком случае говорят, что множества А и В равномощны.
24 -
25 слайд
Мощность множеств
Этот факт позволяет:
установить равенство мощностей двух множеств, не вычисляя этих множеств;
вычислить мощность множества, установив его взаимно-однозначное соответствие с множеством, мощность которого известна или легко вычисляема.
Существование биекции между двумя эквивалентными множествами позволяет переносить изучение свойств с одного множества на другое, когда природа элементов не важна. Например, если |А|=n, то с элементами множества А можно работать как с числами 1,2,…,n.
25 -
26 слайд
Счетные множества
Любое множество, равномощное множеству всех натуральных чисел, называют счетным. Мощность счетного множества обозначают 0 (читается „алеф нуль»).
Если некоторое множество М равномощно множеству натуральных чисел N, то между М и N можно установить взаимно однозначное соответствие (биекцию) : N М, которое называют нумерацией счетного множества М.26
-
27 слайд
Счетные множества
Если элемент множества М есть (n) для некоторого n N, то этот элемент множества М обозначаем через an, называя натуральное число n номером элемента аn относительно данной нумерации .
Таким образом, элементы счетного множества можно перенумеровать, записав их в виде последовательности а1, …, аn, …27
-
28 слайд
Счетные множества
Пример. Множество всех нечетных натуральных чисел счетно. Нумерацию можно задать так: (n) = 2n-1,
N={1, 2, 3, 4, 5, 6, 7, …}
M2n-1- счетно.
M2n-1={1, 3, 5, 7, 9, 11, 13, …}Получили:
M2n-1 N;
M2n-1=N.
Множество равномощно своему подмножеству.
28 -
29 слайд
Счетные множества
Пример. Множество Z всех целых чисел счетно. Расположим элементы множества целых чисел в определенном порядке:N={1, 2, 3, 4, 5, 6, 7, 8, 9, …}
Z={0, -1, 1, -2, 2, -3, 3, -4, 4, … }
Получили:
N Z;
N=Z
Нумерацию можно задать так:— n/2, n- четное
(n) =
(n-1)/2, n — нечетное
29 -
30 слайд
Счетные множества
Пример. Множество Z всех целых чисел счетно.
Нумерацию можно было установить так:Z={…, -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, … }
Получили:
N Z;
N=Z.
1
2
3
4
5
6
7
8
9
10
30 -
31 слайд
Счетные множества
Примеры счетных множеств:
Множество рациональных чисел счетно;
Множество периодических дробей счетно;
Множество всех натуральных чисел, делящихся на заданное число к 2, счетно.
Множество пар натуральных чисел счетно.31
-
32 слайд
Счетные множества
Множество пар натуральных чисел счетно.
32 -
33 слайд
Счетные множества
Теорема .
(а) Подмножество счетного множества конечно или счетно.
(б) Всякое бесконечное множество содержит счетное подмножество.
(в) Объединение конечного или счетного числа конечных или счетных множеств конечно или счетно.
33 -
34 слайд
Несчетные множества
Теорема Кантора: Множество всех действительных чисел интервала (0,1) числовой оси несчетно.
Всякое множество, эквивалентное множеству всех действительных чисел интервала (0,1), называется континуальным или множеством мощности континуума.34
-
35 слайд
Примеры континуальных множеств
Множество действительных чисел;
Множество иррациональных чисел ;
Множество точек на отрезке [0,5];
Множество точек квадрата [1,10]×[1,10];
Множество (М) всех подмножеств некоторого счетного множества М
Множество точек пространства R3.35
-
-
37 слайд
Использованные источники
37
Спирина М. С., Спирин П. А. Дискретная математика: Учебник для студентов учр. среднего проф. образования.- М.:Издат. Центр «Академия», 2018
Москинова Г. И. Дискретная математика: Учебное пособие,-М.:Логос, 2016
Спирина М. С., Спирин П. А. Дискретная математика. Сборник задач с алгоритмами решений (TOP-50). — Издательский центр Академия Москва, 2018. — 288 с. 1-е изд.
Краткое описание документа:
Презентация по дисциплине ОП.08 «Дискретная математика» для специальности 09.02.01 «Компьютерные системы и комплексы» на тему «Соответствия. Свойства соответствий».
Тема «Соответствие. Свойства соответствий. Функции.
Отображения. Типы отображений. Взаимнооднозначные соответствия» изучается в разделе «Основы
теории множеств«. В презентации рассматриваются основные определения: соответствие, область определения и область значения соответствия, образ и прообраз элемента. Рассмотрены основные свойства соответствий: всюду (полностью) определенность, сюръективность, функциональность, инъективность, а так же понятия функции, отображения, взаимнооднозначного соответствия. Все понятия и свойства проиллюстрированы большим количеством примеров.
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
6 265 722 материала в базе
- Выберите категорию:
- Выберите учебник и тему
- Выберите класс:
-
Тип материала:
-
Все материалы
-
Статьи
-
Научные работы
-
Видеоуроки
-
Презентации
-
Конспекты
-
Тесты
-
Рабочие программы
-
Другие методич. материалы
-
Найти материалы
Другие материалы
- 27.10.2020
- 106
- 0

- 27.10.2020
- 91
- 3

- 27.10.2020
- 2943
- 64
- 27.10.2020
- 1027
- 9
- 27.10.2020
- 270
- 11


Вам будут интересны эти курсы:
-
Курс повышения квалификации «Сетевые и дистанционные (электронные) формы обучения в условиях реализации ФГОС по ТОП-50»
-
Курс профессиональной переподготовки «Информационные технологии в профессиональной деятельности: теория и методика преподавания в образовательной организации»
-
Курс повышения квалификации «Использование компьютерных технологий в процессе обучения в условиях реализации ФГОС»
-
Курс повышения квалификации «Специфика преподавания информатики в начальных классах с учетом ФГОС НОО»
-
Курс повышения квалификации «Введение в программирование на языке С (СИ)»
-
Курс профессиональной переподготовки «Управление в сфере информационных технологий в образовательной организации»
-
Курс повышения квалификации «Современные тенденции цифровизации образования»
-
Курс повышения квалификации «Специфика преподавания дисциплины «Информационные технологии» в условиях реализации ФГОС СПО по ТОП-50»
-
Курс повышения квалификации «Современные языки программирования интегрированной оболочки Microsoft Visual Studio C# NET., C++. NET, VB.NET. с использованием структурного и объектно-ориентированного методов разработки корпоративных систем»
-
Курс повышения квалификации «Применение интерактивных образовательных платформ на примере платформы Moodle»





































![GR+R+Найти образы и прообразы чисел: 0, 1, 2; отрезков: [0,1], [2,3] 13 GR+R+Найти образы и прообразы чисел: 0, 1, 2; отрезков: [0,1], [2,3] 13](https://documents.infourok.ru/abfd0012-3f4b-425e-86be-4e48814caf32/0/slide_13.jpg)























