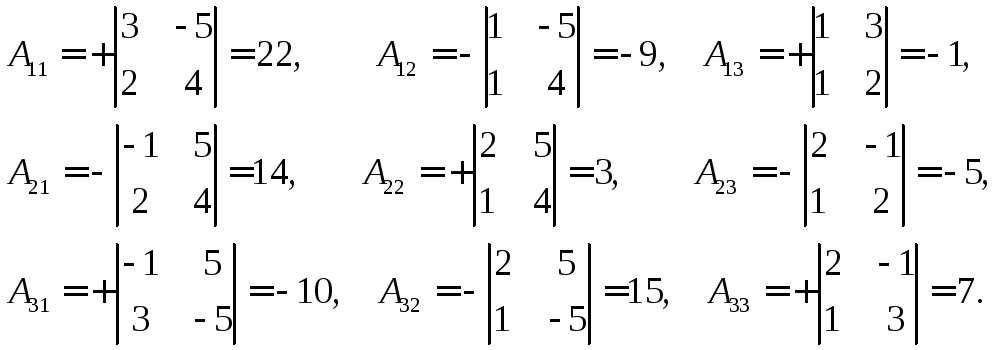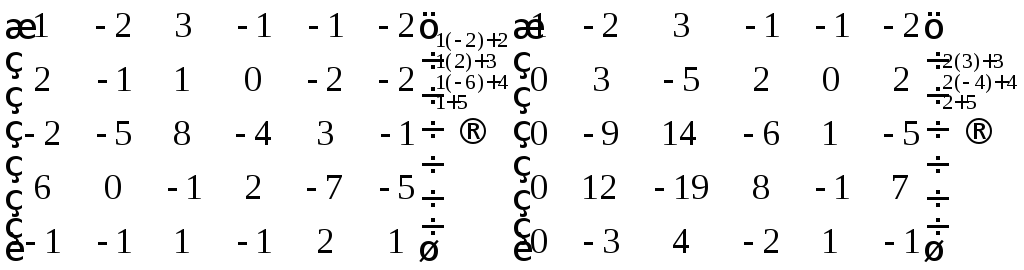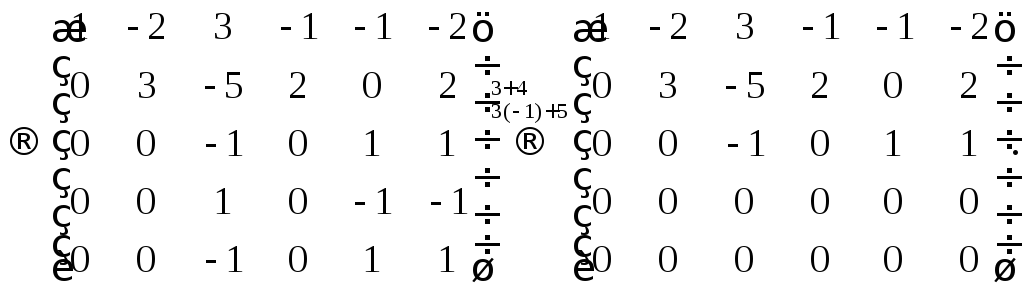Матрица
называется обратнойк квадратной матрице
,
если
,
где
— единичная матрица, имеющая тот же
порядок, что и матрица. Обратная
матрица существует только в том случае,
если,
и ее элементы находятся по формуле
,
где
— алгебраическое дополнение к элементу
.
Внимание! Алгебраические дополнения
вычисляются к элементам строки, а
записываются в столбец.
Если
,
то матрицаназываетсявырожденной,
в противном случаеневырожденной,т.е. обратная матрица существует только
для невырожденных матриц.
Обозначается обратная матрица
,
т.е.
,
при этом ее определитель
.
Для невырожденных матриц
и
выполнены соотношения
,
.
Введение обратной матрицы позволяет
решать матричные уравнения. В конечном
счете, матричные уравнения сводятся к
двум простейшим уравнениям:
или
.
Если матрица
— квадратная, невырожденная, то эти
уравнения имеют единственное решение,
которое можно получить с помощью обратной
матрицы. Так как при умножении матриц
коммутативный закон не выполняется,
указанные уравнения имеют различные
решения.
При поиске решения первое из уравнений
надо умножать на обратную матрицу
слева, а второе справа, т.е.
,
(5)
.
(6)
►Пример 5. Найти решение матричного
уравнения,
то есть определить матрицу,
если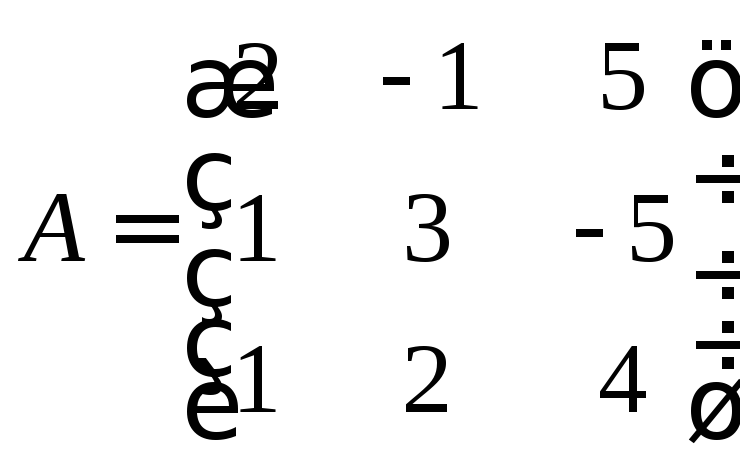
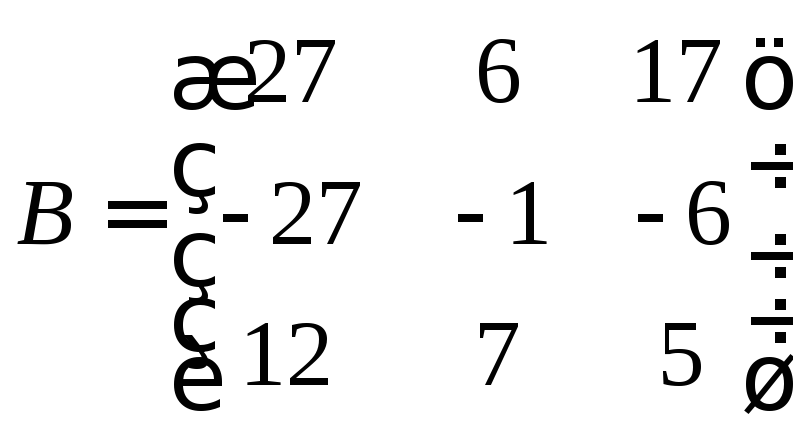
Решение.
Решение в матричном виде определяется
формулой (5), т.е.
,
если матрицаневырожденная. Вычислим определитель
матрицы:
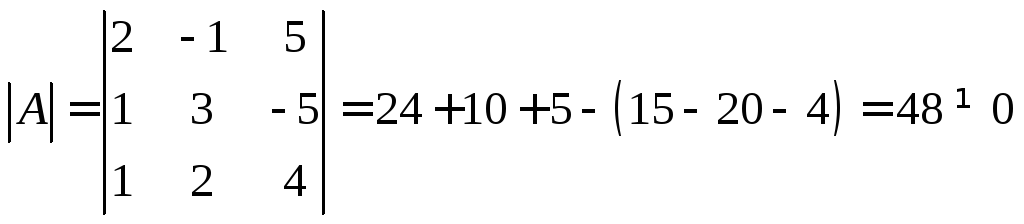
Следовательно, матрица
невырожденная, и для нее существует
обратная матрица. Проведем вычисления,
необходимые для построения обратной
матрицы. Вычислим алгебраические
дополнения:
Составим обратную матрицу
и
найдем неизвестную матрицу.
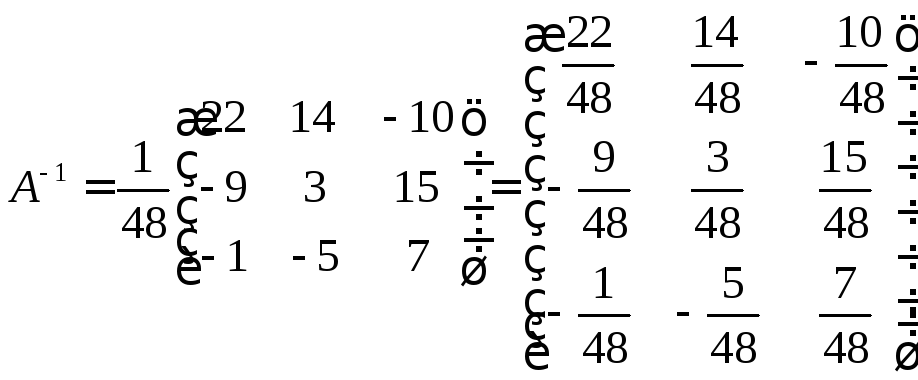
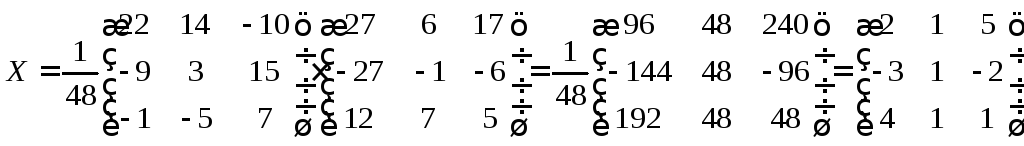
◄
При вычислениях множитель
лучше оставлять перед матрицей и
проводить умножение полученной матрицы
на него на последнем этапе вычислений.
Упражнения.
1. Для заданных матриц найти обратную
матрицу:
а)
;
б)
;
в)
;
г)
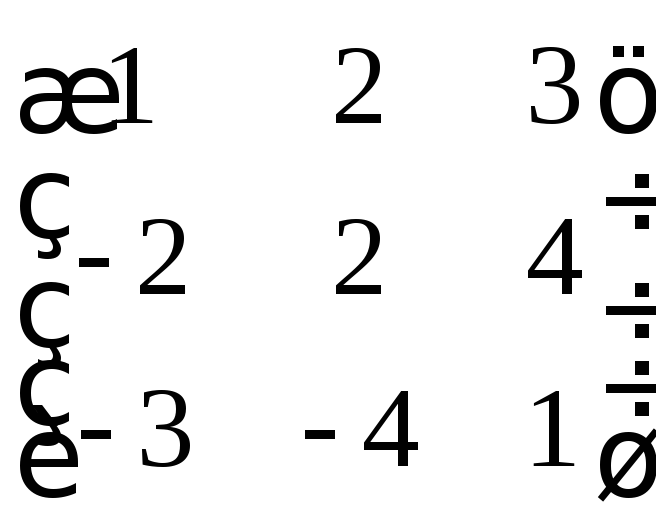
д)

Ответы:
а)
;
б) ; в)
;
г)
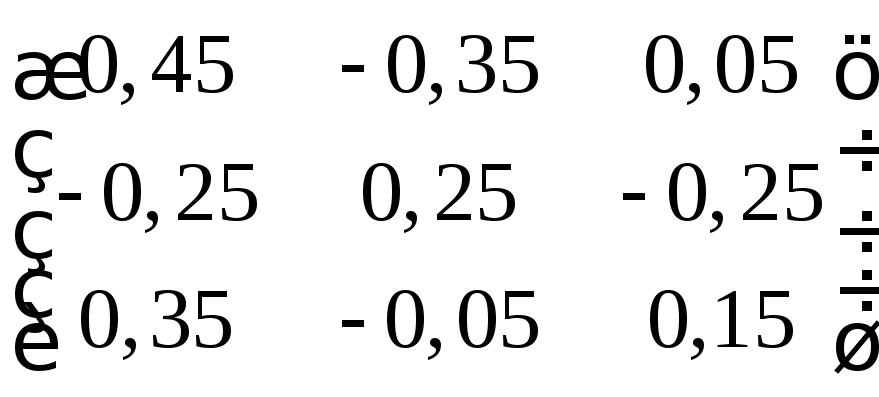
д)
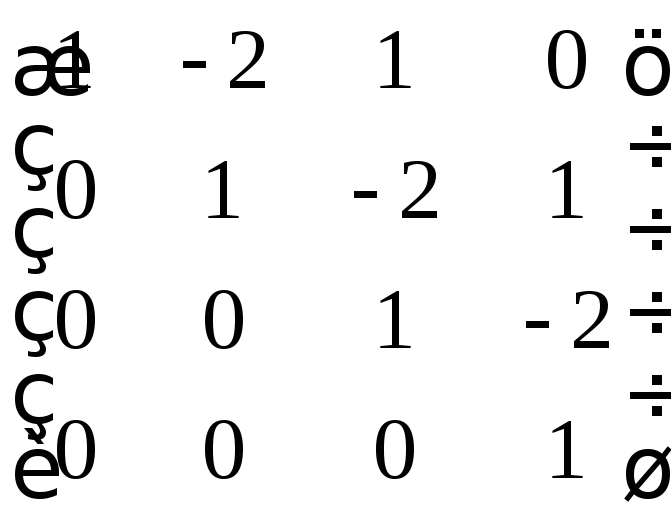
2. Найти неизвестную матрицу из уравнений:
а)
;
б);
в);
г)
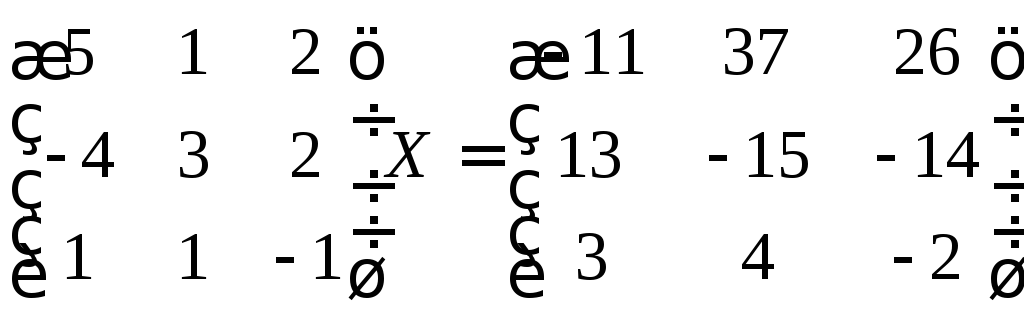
д)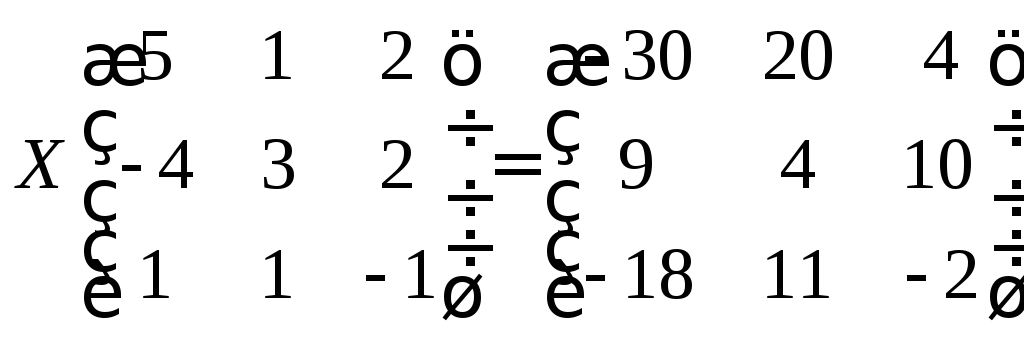
Ответы: а);
б);
в);
г)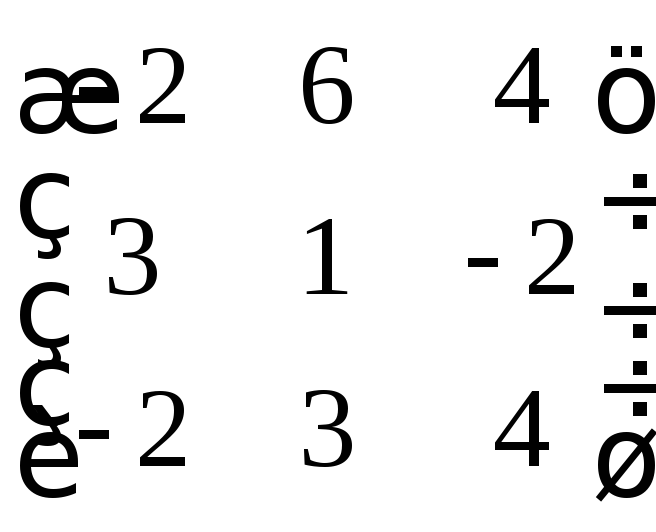
д)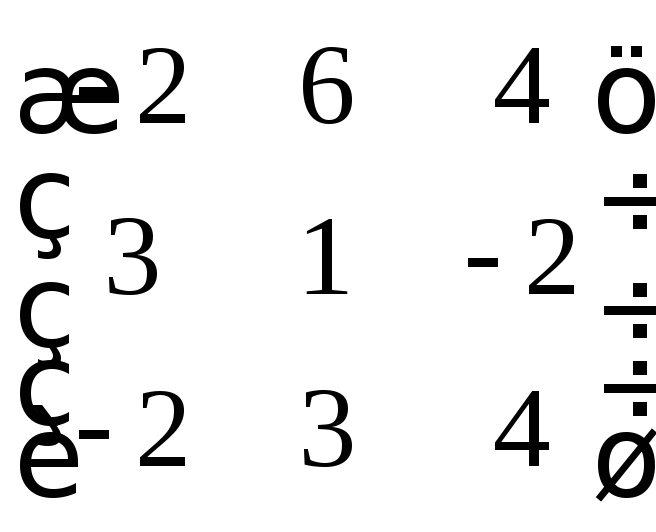
4. Ранг матрицы
Рангомматрицы(обозначение:
)
называетсяпорядок отличного от
нуля минора этой матрицы при условии,
что все ее миноры более высоких порядков
равны нулю. Минор наивысшего порядка,
отличный от нуля, называетсябазисным
миноромили просто базисом.
Матрица может иметь несколько различных
базисов. Для определения базиса над
матрицей производятэлементарные
преобразования, при которых ранг
матрицы не изменяется.
К элементарным
преобразованиямматрицы относятся:
— транспонирование;
— удаление или добавление строки
(столбца), состоящей из нулей;
— умножение строки (столбца) на число,
отличное от нуля;
— перестановка строк (столбцов);
-прибавление к элементам какой-либо
строки элементов другой строки,
умноженных на постоянное число (то же
самое для столбцов).
Выполняя элементарные преобразования
над матрицей, получаем другую матрицу,
называемую эквивалентной.
Переход от исходной матрицы к эквивалентной
будем обозначать символом.
Используя выше перечисленные действия,
матрицу можно преобразовать к треугольному
виду, что позволяет легко определить
ее ранг.
►Пример 7.Найти ранг матрицы
Решение.
Преобразуем матрицу:
Минор
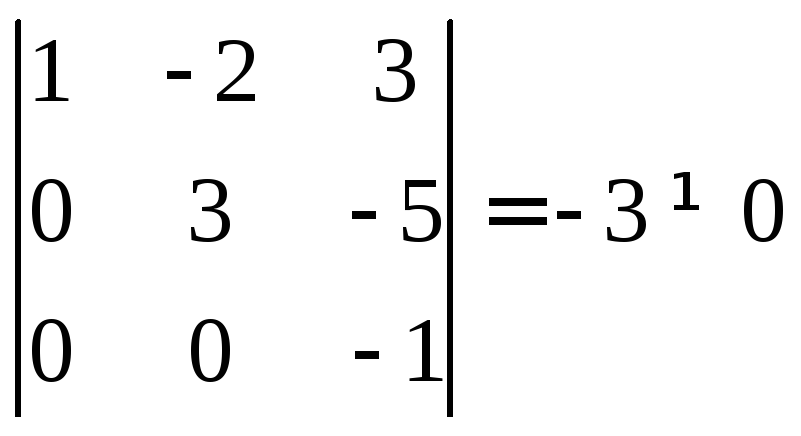
а все миноры четвертого порядка равны
нулю, т.к. содержат нулевую строку.
Следовательно,.
◄
При преобразовании матрицы мы проводили
операции только со строками и по
определенному алгоритму. Этот метод
стандартный, но не является обязательным.
Упражнения.
1. Найти ранг матриц:
а)
б)
в)
г)
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Заказать задачи по любым предметам можно здесь от 10 минут
Как найти обратную матрицу
- Быстрый способ для матриц $2 times 2$
- Пример 1
- Пример 2
- Нахождение с помощью метода Гаусса
- Пример 3
- Пример 4
- Метод союзной матрицы(алгебраические дополнения)
- Пример 5
Обратная матрица обозначается $ A^{-1} $ и существует только для матриц, у которых определитель не равен нулю $ det A neq 0 $.
Быстрый способ для матриц $2 times 2$
Пусть задана матрица $A = begin{pmatrix} a&b\c&d end{pmatrix}$. Для быстрого способа нахождения обратной матрицы необходимо поменять местами элементы стоящие на главной диагонали, а для оставшихся элементов поменять знак на противоположный. Затем каждый элемент разделить матрицы разделить на определитель исходной матрицы. Математическая формула выглядит следующим образом $$A^{-1} = frac{1}{det A} begin{pmatrix} d&-b \ -c&a end{pmatrix} = frac{1}{ad-bc} begin{pmatrix} d&-b \ -c&a end{pmatrix}.$$
| Пример 1 |
| Найти обратную матрицу для $A = begin{pmatrix} 3&4 \ 5&9 end{pmatrix}$. |
| Решение |
|
Первым делом вычисляем определитель и убеждаемся, что он не равен нулю $$det A = begin{vmatrix} 3&4 \ 5&9 end{vmatrix} = 3cdot9 — 4cdot5 = 27 — 20 = 7.$$ Итак, определитель не равен нулю, значит, обратная матрица существует. Продолжаем наш алгоритм. Меняем элементы на главной диагонали местами, а у оставшихся элементов меняем знак на противоположный. $$A^{-1} = frac{1}{7} begin{pmatrix} 9&-4 \ -5&3 end{pmatrix} = begin{pmatrix} frac{9}{7}&frac{-4}{7} \ frac{-5}{7}&frac{3}{7} end{pmatrix}.$$ |
| Ответ |
| $$A^{-1} = begin{pmatrix} frac{9}{7}&frac{-4}{7} \ frac{-5}{7}&frac{3}{7} end{pmatrix}$$ |
| Пример 2 |
| Вычислить обратную матрицу для $A = begin{pmatrix} 2&-1 \ 4&-6 end{pmatrix}$. |
| Решение |
|
Находим определитель $$det A = begin{vmatrix} 2&-1 \ 4&-6 end{vmatrix} = 2cdot(-6) — 4cdot(-1) = -12 + 4 = -8.$$ Меняем местами элементы главной диагонали, а остальным меняем знак на противоположный. Не забываем затем каждый элемент разделить на определитель. $$A^{-1} = frac{1}{-8} begin{pmatrix} -6&1 \ -4&2 end{pmatrix} = begin{pmatrix} frac{-6}{-8}&frac{1}{-8} \ frac{-4}{-8}&frac{2}{-8} end{pmatrix} = begin{pmatrix} frac{3}{4}&-frac{1}{8} \ frac{1}{2}&-frac{1}{4} end{pmatrix}$$ |
| Ответ |
| $$A^{-1} = begin{pmatrix} frac{3}{4}&-frac{1}{8} \ frac{1}{2}&-frac{1}{4} end{pmatrix}$$ |
Нахождение с помощью метода Гаусса
На практике чаще всего метод Гаусса используется как способ нахождения обратной матрицы. Суть метода в том, что к основной матрице добавляется дополнительная единичная матрица с такой же размерностью.
$$ Bigg (begin{matrix} a_{11}&a_{12}&a_{13}\a_{21}&a_{22}&a_{23}\a_{31}&a_{32}&a_{33} end{matrix} Bigg | begin{matrix} 1&0&0\0&1&0\0&0&1 end{matrix} Bigg ) $$
Далее нужно путем простейших элементарных преобразований привести левую матрицу к единичной, а одновременно с ней справа получится обратная матрица:
$$ Bigg (begin{matrix} 1&0&0\0&1&0\0&0&1 end{matrix} Bigg | begin{matrix} b_{11}&b_{12}&b_{13}\b_{21}&b_{22}&b_{23}\b_{31}&b_{32}&b_{33} end{matrix} Bigg ) $$
$$A^{-1} = begin{pmatrix} b_{11}&b_{12}&b_{13}\b_{21}&b_{22}&b_{23}\b_{31}&b_{32}&b_{33} end{pmatrix}$$
| Пример 3 |
| Найти обратную матрицу элементарными преобразованиями $$A = begin{pmatrix} 2&-1&0 \ 0&2&-1 \ -1&-1&1 end{pmatrix}.$$ |
| Решение |
|
Вычисляем определитель матрицы, чтобы убедиться что он не равен нулю $$det A = begin{vmatrix} 2&-1&0 \ 0&2&-1 \ -1&-1&1 end{vmatrix} = 4-1+0-0-2-0=1 neq 0.$$ Выписываем основную матрицу и добавляем справа единичную матрицу. $$begin{pmatrix} 2&-1&0 &|& 1&0&0 \ 0&2&-1 &|& 0&1&0 \ -1&-1&1 &|& 0&0&1 end{pmatrix}$$ Проводим элементарные преобразования над строками матриц таким образом, чтобы слева получилась единичная матрица. В то же время как справа получим обратную матрицу. Умножаем третью строку на 2 и прибавляем первую. $$begin{pmatrix} 2&-1&0 &|& 1&0&0 \ 0&2&-1 &|& 0&1&0 \ 0&-3&2 &|& 1&0&2 end{pmatrix}$$ Умножаем третью строку на 2 и прибавляем к ней вторую строку, умноженную на 3. $$begin{pmatrix} 2&-1&0 &|& 1&0&0 \ 0&2&-1 &|& 0&1&0 \ 0&0&1 &|& 2&3&4 end{pmatrix}$$ Теперь запускаем обратный ход преобразований снизу вверх. Ко второй строке прибавляем третью. $$begin{pmatrix} 2&-1&0 &|& 1&0&0 \ 0&2&0 &|& 2&4&4 \ 0&0&1 &|& 2&3&4 end{pmatrix}$$ Умножаем первую строку на 2 и прибавляем к ней вторую строчку матрицы. $$begin{pmatrix} 4&0&0 &|& 4&4&4 \ 0&2&0 &|& 2&4&4 \ 0&0&1 &|& 2&3&4 end{pmatrix}$$ Теперь, чтобы слева получилась единичная матрица нужно первую строку разделить на 4, вторую на 2. $$begin{pmatrix} 1&0&0 &|& 1&1&1 \ 0&1&0 &|& 1&2&2 \ 0&0&1 &|& 2&3&4 end{pmatrix}$$ Справа как видим получилась обратная матрица $$A^{-1} = begin{pmatrix} 1&1&1 \ 1&2&2 \ 2&3&4 end{pmatrix}.$$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$A^{-1} = begin{pmatrix} 1&1&1 \ 1&2&2 \ 2&3&4 end{pmatrix}$$ |
| Пример 4 |
| Дана матрица, найти обратную $$A = begin{pmatrix} 3&2&1 \ 1&0&2 \ 4&1&3 end{pmatrix}.$$ |
| Решение |
|
Первым делом вычисляем определитель, чтобы убедиться в существовании обратной матрицы $$det A = begin{vmatrix} 3&2&1 \ 1&0&2 \ 4&1&3 end{vmatrix} = 0+16+1-0-6-6=5.$$ Теперь справа от матрицы дописываем единичную матрицу $$begin{pmatrix} 3&2&1 &|& 1&0&0 \ 1&0&2 &|& 0&1&0 \ 4&1&3 &|& 0&0&1 end{pmatrix}.$$ Теперь с помощью элементарных преобразований делаем так, чтобы слева стояла единичная матрица. А справа получим одновременно обратную матрицу. Умножаем вторую строку на 3 и вычитаем из неё первую. Умножаем третью строчку на 3 и вычитаем первую, умноженную на 4. $$begin{pmatrix} 3&2&1 &|& 1&0&0 \ 0&-2&5 &|& -1&3&0 \ 0&-5&5 &|& -4&0&3 end{pmatrix}$$ Умножаем третью строку на 2 и вычитаем вторую, умноженную на 5. $$begin{pmatrix} 3&2&1 &|& 1&0&0 \ 0&-2&5 &|& -1&3&0 \ 0&0&-15 &|& -3&-15&6 end{pmatrix}$$ Третью строку можно разделить на 3, чтобы уменьшить числа для дальнейшего удобства. Сделаем это. $$begin{pmatrix} 3&2&1 &|& 1&0&0 \ 0&-2&5 &|& -1&3&0 \ 0&0&-5 &|& -1&-5&2 end{pmatrix}$$ Начинаем проводить преобразования над строками теперь снизу вверх. Умножаем первую строку на 5 и прибавляем к ней третью. Ко второй строке просто прибавляем третью. $$begin{pmatrix} 15&10&0 &|& 4&-5&2 \ 0&-2&0 &|& -2&-2&2 \ 0&0&-5 &|& -1&-5&2 end{pmatrix}$$ К первой строке прибавляем вторую, умноженную на 5. $$begin{pmatrix} 15&0&0 &|& -6&-15&12 \ 0&-2&0 &|& -2&-2&2 \ 0&0&-5 &|& -1&-5&2 end{pmatrix}$$ Осталось разделить первую строку на 15, вторую на (-2), а третью на (-5). $$begin{pmatrix} 1&0&0 &|& -frac{2}{5}&-1&frac{4}{5} \ 0&1&0 &|& 1&1&-1 \ 0&0&1 &|& frac{1}{5}&1&-frac{2}{5} end{pmatrix}$$ |
| Ответ |
| $$begin{pmatrix} 1&0&0 &|& -frac{2}{5}&-1&frac{4}{5} \ 0&1&0 &|& 1&1&-1 \ 0&0&1 &|& frac{1}{5}&1&-frac{2}{5} end{pmatrix}$$ |
Метод союзной матрицы(алгебраические дополнения)
Формула нахождения обратной матрицы через алгебраические дополнения выглядит следующим образом
$$A^{-1} = frac{1}{|A|} (A^*)^T. $$
Матрица $A^*$ называется союзной (присоединенной) матрицей и представляет собой набор алгебраических дополнений матрицы $ A $:
$$ A^* = begin{pmatrix} A_{11}&A_{12}&A_{13}\A_{21}&A_{22}&A_{23}\A_{31}&A_{22}&A_{33} end{pmatrix}, text{ где } A_{ij}=(-1)^{i+j} M_{ij} $$
$M_{ij} $ называется минором матрицы, который получается путем вычеркивания $ i $-ой строки и $ j $-того столбца из матрицы.
| Пример 5 |
| Найти обратную матрицу методом алгебраических дополнений $$ A = begin{pmatrix} 3&1&2\-1&3&-2\0&-1&4 end{pmatrix} $$ |
| Решение |
|
Итак, пользуемся формулой $ A^{-1} = frac{1}{|A|} (A^*)^T $ Первым делом вычисляем определитель матрицы $ A $, так как необходимым условием существование обратной матрицы является неравенство его к нулю: $$ |A| = begin{vmatrix} 3&1&2\-1&3&-2\0&-1&4 end{vmatrix} = 36 + 0 + 2 — 0 — 6 + 4 = 36 neq 0 $$ Находим алгебраические дополнения матрицы $ A $. Для этого удаляем все элементы стоящие в i-ой строке и в j-ом столбце. Оставшиеся элементы матрицы переписываем в определитель и проводим его вычисление. Вычеркиваем первую строку и первый столбец: $$ A_{11} = (-1)^{1+1} cdot begin{vmatrix} 3&-2\-1&4 end{vmatrix} = 12 — 2 = 10 $$ Убираем первую строку и второй столбец: $$ A_{12} = (-1)^{1+2} cdot begin{vmatrix} -1&-2\0&4 end{vmatrix} = -(-4 — 0) = 4 $$ Оставшиеся алгебраические дополнения находим по аналогии с предыдущими двумя. $$ A_{13} = (-1)^{1+3} cdot begin{vmatrix} -1&3\0&-1 end{vmatrix} = 1 — 0 = 1 $$ $$ A_{21} = (-1)^{2+1} cdot begin{vmatrix} 1&2\-1&4 end{vmatrix} = -(4 + 2) = -6 $$ $$ A_{22} = (-1)^{2+2} cdot begin{vmatrix} 3&2\0&4 end{vmatrix} = 12 — 0 = 12 $$ $$ A_{23} = (-1)^{2+3} cdot begin{vmatrix} 3&1\0&-1 end{vmatrix} = -(-3 — 0) = 3 $$ $$ A_{31} = (-1)^{3+1} cdot begin{vmatrix} 1&2\3&-2 end{vmatrix} = -2 — 6 = -8 $$ $$ A_{32} = (-1)^{3+2} cdot begin{vmatrix} 3&2\-1&-2 end{vmatrix} = -(-6 + 2) = 4 $$ $$ A_{33} = (-1)^{3+3} cdot begin{vmatrix} 3&1\-1&3 end{vmatrix} = 9+1 = 10 $$ Составляем союзную (присоединенную) матрицу $ A^* $ из алгебраических дополнений: $$ A^* = begin{pmatrix} 10&4&1\-6&12&3\-8&4&10 end{pmatrix}. $$ Транспонируем её и обозначаем $ (A^*)^T $: $$ (A^*)^T = begin{pmatrix} 10&-6&-8\4&12&4\1&3&10 end{pmatrix} $$ В итоге находим обратную матрицу $ A^{-1} $: $$ A^{-1} = frac{1}{36} begin{pmatrix} 10&-6&-8\4&12&4\1&3&10 end{pmatrix} $$ Делим каждый элемент матрицы на 36 и получаем следующее: $$begin{pmatrix} frac{5}{18}&-frac{1}{6}&-frac{2}{9}\ frac{1}{9}&frac{1}{3}&frac{1}{9}\frac{1}{36}&frac{1}{12}&frac{5}{18} end{pmatrix}.$$ |
| Ответ |
| $$A^{-1} =begin{pmatrix} frac{5}{18}&-frac{1}{6}&-frac{2}{9}\ frac{1}{9}&frac{1}{3}&frac{1}{9}\frac{1}{36}&frac{1}{12}&frac{5}{18} end{pmatrix}$$ |
Содержание:
- Нахождение обратной матрицы с помощью присоединённой матрицы
- Нахождение обратной матрицы с помощью союзной матрицы
- Облегченный способ для матрицы второго порядка
Обратную матрицу
можно найти с помощью двух ниже описанных методов.
Нахождение обратной матрицы с помощью присоединённой матрицы
Пример
Задание. Для матрицы $ A=left( begin{array}{ll}{7} & {4} \ {5} & {3}end{array}right) $
найти обратную методом присоединенной матрицы.
Решение. Приписываем к заданной матрице

единичную матрицу второго порядка:
$$ Aleft|E=left( begin{array}{cc|cc}{7} & {4} & {1} & {0} \ {5} & {3} & {0} & {1}end{array}right)right. $$
От первой строки отнимаем вторую (для этого от элемента первой строки отнимаем соответствующий элемент второй строки):
$$ Aleft|E = left( begin{array}{rr|rr}{2} & {1} & {1} & {-1} \ {5} & {3} & {0} & {1}end{array}right)right. $$
От второй строки отнимаем две первых:
$$ Aleft|E sim left( begin{array}{rr|rr}{2} & {1} & {1} & {-1} \ {1} & {1} & {-2} & {3}end{array}right)right. $$
Первую и вторую строки меняем местами:
$$ Aleft|E sim left( begin{array}{rr|rr}{1} & {1} & {-2} & {3} \ {2} & {1} & {1} & {-1}end{array}right)right. $$
От второй строки отнимаем две первых:
$$ Aleft|E sim left( begin{array}{rr|rr}{1} & {1} & {-2} & {3} \ {0} & {-1} & {5} & {-7}end{array}right)right. $$
Вторую строку умножаем на (-1), а к первой строке прибавляем вторую:
$$ Aleft|E sim left( begin{array}{rr|rr}{1} & {0} & {3} & {-4} \ {0} & {1} & {-5} & {7}end{array}right)right. $$
Итак, слева получили единичную матрицу, а значит матрица, стоящая в
правой части (справа от вертикальной черты), является обратной к исходной.
Таким образом, получаем, что $ A^{-1}=left( begin{array}{rr}{3} & {-4} \ {-5} & {7}end{array}right) $
Ответ. $ A^{-1}=left( begin{array}{rr}{3} & {-4} \ {-5} & {7}end{array}right) $
Замечание
Если на некотором этапе в «левой» матрице получается
нулевая строка, то это
означает, что исходная матрица обратной не имеет.
Облегченный способ для матрицы второго порядка
Для матрицы второго порядка можно немного облегчить нахождение обратной, используя следующий алгоритм:
Шаг 1. Находим определитель $ Delta $ заданной матрицы,
если он равен нулю, то делаем вывод, что обратной матрицы не существует, иначе переходим к следующему шагу.
Шаг 2. Элементы, стоящие на
главной диагонали меняем местами, а у элементов
побочной диагонали меняем знак на противоположный.
Шаг 3. Делим все элементы на $ Delta $ и получаем обратную матрицу.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Найти обратную матрицу для
$ A=left( begin{array}{ll}{1} & {2} \ {2} & {4}end{array}right) $
Решение. Шаг 1. $ Delta=left| begin{array}{ll}{1} & {2} \ {2} & {4}end{array}right|=4-4=0 $ ,
тогда обратной матрицы не существует.
Ответ. Так как
определитель матрицы $A$ равен нулю,
то она не имеет обратной.
Пример
Задание. Найти обратную матрицу для $ A=left( begin{array}{ll}{1} & {1} \ {1} & {2}end{array}right) $
Решение. Шаг 1. Находим определитель: $ Delta=left| begin{array}{ll}{1} & {1} \ {1} & {2}end{array}right|=2-1=1 neq 0 $
Шаг 2. $ A^{prime}=left( begin{array}{rr}{2} & {-1} \ {-1} & {1}end{array}right) $
Шаг 3. $ A^{-1}=frac{1}{Delta} cdot A^{prime}=left( begin{array}{rr}{2} & {-1} \ {-1} & {1}end{array}right) $
Ответ. $ A^{-1}=left( begin{array}{rr}{2} & {-1} \ {-1} & {1}end{array}right) $
Нахождение обратной матрицы с помощью союзной матрицы
Определение
Матрица $ tilde{A} $ называется lt strong>союзной lt /strong> к квадратной матрице $A$ ,
если элементы матрицы $ tilde{A} $ равны
алгебраическим дополнениям соответствующих
элементов матрицы $A$ .
$$ A=left( begin{array}{ccc}{a_{11}} & {a_{12}} & {a_{13}} \ {a_{21}} & {a_{22}} & {a_{23}} \ {a_{31}} & {a_{32}} & {a_{33}}end{array}right) Rightarrow tilde{A}=left( begin{array}{ccc}{A_{11}} & {A_{12}} & {A_{13}} \ {A_{21}} & {A_{22}} & {A_{23}} \ {A_{31}} & {A_{32}} & {A_{33}}end{array}right) $$
Имеет место следующее свойство: $ A cdot widetilde{A}^{T}=|A| cdot E $
Тогда, если $ |A| neq 0 $ , то
$ A cdot tilde{A}^{T} cdot frac{1}{|A|}=E $ , а тогда
$ A^{-1}=frac{1}{|A|} cdot tilde{A}^{T} $
Таким образом, матрица имеет союзную тогда и только тогда, когда она
невырожденная.
Пример
Задание. Найти обратную матрицу к матрице $ A=left( begin{array}{rrr}{1} & {0} & {2} \ {2} & {-1} & {1} \ {1} & {3} & {-1}end{array}right) $
Решение. Вычисляем определитель матрицы:
$$ Delta=left| begin{array}{rrr}{1} & {0} & {2} \ {2} & {-1} & {1} \ {1} & {3} & {-1}end{array}right|=1 cdot(-1) cdot(-1)+2 cdot 3 cdot 2+0 cdot 1 cdot 1- $$
$$ -1 cdot(-1) cdot 2-3 cdot 1 cdot 1-2 cdot 0 cdot(-1)=1+12+0+2-3+0=12 neq 0 $$
Так как определитель не равен нулю, то матрица имеет обратную.
Обратная матрица $A^{-1}$ к матрице
$A$ находится по формуле:
$$ A^{-1}=frac{1}{Delta} cdot widetilde{A}^{T} $$
Найдем союзную матрицу $ tilde{A} $ , для этого вычислим алгебраические
дополнения к элементам матрицы $A$ :
$$ A_{11}=(-1)^{1+1} left| begin{array}{rr}{-1} & {1} \ {3} & {-1}end{array}right|=(-1) cdot(-1)-3 cdot 1=1-3=-2 $$
$$ A_{12}=(-1)^{1+2} left| begin{array}{rr}{2} & {1} \ {1} & {-1}end{array}right|=-[2 cdot(-1)-1 cdot 1]=-(-2-1)=3 $$
$$ A_{13}=(-1)^{1+3} left| begin{array}{rr}{2} & {-1} \ {1} & {3}end{array}right|=2 cdot 3-1 cdot(-1)=6+1=7 $$
$$ A_{21}=(-1)^{2+1} left| begin{array}{rr}{0} & {2} \ {3} & {-1}end{array}right|=-[0 cdot(-1)-3 cdot 2]=-(0-6)=6 $$
$$ A_{22}=(-1)^{2+2} left| begin{array}{rr}{1} & {2} \ {1} & {-1}end{array}right|=1 cdot(-1)-1 cdot 2=-1-2=-3 $$
$$ A_{23}=(-1)^{2+3} left| begin{array}{cc}{1} & {0} \ {1} & {3}end{array}right|=-[1 cdot 3-1 cdot 0]=-(3-0)=-3 $$
$$ A_{31}=(-1)^{3+1} left| begin{array}{rr}{0} & {2} \ {-1} & {1}end{array}right|=0 cdot 1-(-1) cdot 2=0+2=2 $$
$$ A_{32}=(-1)^{3+2} left| begin{array}{cc}{1} & {2} \ {2} & {1}end{array}right|=-[1 cdot 1-2 cdot 2]=-(1-4)=3 $$
$$ A_{33}=(-1)^{3+3} left| begin{array}{rr}{1} & {0} \ {2} & {-1}end{array}right|=1 cdot(-1)-2 cdot 0=-1-0=-1 $$
Таким образом, $ tilde{A}=left( begin{array}{rrr}{-2} & {3} & {7} \ {6} & {-3} & {-3} \ {2} & {3} & {-1}end{array}right) $
Транспонируем эту матрицу (т.е. строки матрицы делаем столбцами с тем же номером):
$$ widetilde{A}^{T}=left( begin{array}{rrr}{-2} & {6} & {2} \ {3} & {-3} & {3} \ {7} & {-3} & {-1}end{array}right) $$
Итак, $ A^{-1}=frac{1}{12} left( begin{array}{rrr}{-2} & {6} & {2} \ {3} & {-3} & {3} \ {7} & {-3} & {-1}end{array}right) $
Ответ. $ A^{-1}=frac{1}{12} left( begin{array}{rrr}{-2} & {6} & {2} \ {3} & {-3} & {3} \ {7} & {-3} & {-1}end{array}right) $
Читать дальше: линейно зависимые и линейно независимые строки.