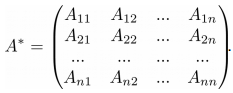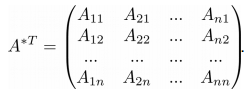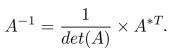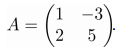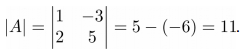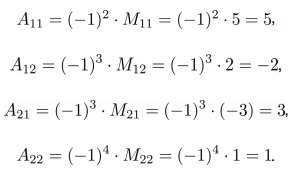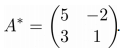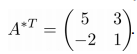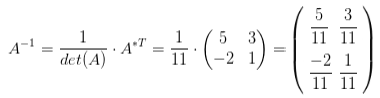Как найти обратную матрицу программа

#include<stdio.h>
int main()
{
    int matrix[20][20], r,a;
    int i, j, k, m;
    scanf_s("%d", &m);
    for(i = 0; i < m; i++)
    {
        for(j = 0; j < m; j++)
        {
            scanf_s("%i", &matrix[i][j]);
        }
    }
    for(i = 0; i < m; i++)
    {
        for(j = m; j < 2*m; j++)
        {
            if(i == (j - m))
                matrix[i][j] = 1;
            else
                matrix[i][j] = 0;
        }
    }
    for(i = 0; i < m; i++)
    {
        for(j = 0; j < m; j++)
        {
            if(i != j)
            {
                r = matrix[j][i]/matrix[i][i];
                for(k = 0; k < 2*m; k++)
                {
                    matrix[j][k] -= r * matrix[i][k];
                }
            }
        }
    }
    for(i = 0; i < m; i++)
    {
        a = matrix[i][i];
        for(j = 0; j < 2*m; j++)
        {
            matrix[i][j] /= a;
        }
    }
    for(i = 0; i < m; i++)
    {
        for(j = m; j < 2*m; j++)
        {
            printf("%it", matrix[i][j]);
        }
        printf("n");
    }
    return 0;
}

//Title: Matrix Header File
//Writer: Say OL
//This is a beginner code not an expert one
//No responsibilty for any errors
//Use for your own risk
using namespace std;
int row,col,Row,Col;
double Coefficient;
//Input Matrix
void Input(double Matrix[9][9],int Row,int Col)
{
    for(row=1;row<=Row;row++)
        for(col=1;col<=Col;col++)
        {
            cout<<"e["<<row<<"]["<<col<<"]=";
            cin>>Matrix[row][col];
        }
}
//Output Matrix
void Output(double Matrix[9][9],int Row,int Col)
{
    for(row=1;row<=Row;row++)
    {
        for(col=1;col<=Col;col++)
            cout<<Matrix[row][col]<<"t";
        cout<<endl;
    }
}
//Copy Pointer to Matrix
void CopyPointer(double (*Pointer)[9],double Matrix[9][9],int Row,int Col)
{
    for(row=1;row<=Row;row++)
        for(col=1;col<=Col;col++)
            Matrix[row][col]=Pointer[row][col];
}
//Copy Matrix to Matrix
void CopyMatrix(double MatrixInput[9][9],double MatrixTarget[9][9],int Row,int Col)
{
    for(row=1;row<=Row;row++)
        for(col=1;col<=Col;col++)
            MatrixTarget[row][col]=MatrixInput[row][col];
}
//Transpose of Matrix
double MatrixTran[9][9];
double (*(Transpose)(double MatrixInput[9][9],int Row,int Col))[9]
{
    for(row=1;row<=Row;row++)
        for(col=1;col<=Col;col++)
            MatrixTran[col][row]=MatrixInput[row][col];
    return MatrixTran;
}
//Matrix Addition
double MatrixAdd[9][9];
double (*(Addition)(double MatrixA[9][9],double MatrixB[9][9],int Row,int Col))[9]
{
    for(row=1;row<=Row;row++)
        for(col=1;col<=Col;col++)
            MatrixAdd[row][col]=MatrixA[row][col]+MatrixB[row][col];
    return MatrixAdd;
}
//Matrix Subtraction
double MatrixSub[9][9];
double (*(Subtraction)(double MatrixA[9][9],double MatrixB[9][9],int Row,int Col))[9]
{
    for(row=1;row<=Row;row++)
        for(col=1;col<=Col;col++)
            MatrixSub[row][col]=MatrixA[row][col]-MatrixB[row][col];
    return MatrixSub;
}
//Matrix Multiplication
int mRow,nCol,pCol,kcol;
double MatrixMult[9][9];
double (*(Multiplication)(double MatrixA[9][9],double MatrixB[9][9],int mRow,int nCol,int pCol))[9]
{
    for(row=1;row<=mRow;row++)
        for(col=1;col<=pCol;col++)
        {
            MatrixMult[row][col]=0.0;
            for(kcol=1;kcol<=nCol;kcol++)
                MatrixMult[row][col]+=MatrixA[row][kcol]*MatrixB[kcol][col];
        }
    return MatrixMult;
}
//Interchange Two Rows
double RowTemp[9][9];
double MatrixInter[9][9];
double (*(InterchangeRow)(double MatrixInput[9][9],int Row,int Col,int iRow,int jRow))[9]
{
    CopyMatrix(MatrixInput,MatrixInter,Row,Col);
    for(col=1;col<=Col;col++)
    {
        RowTemp[iRow][col]=MatrixInter[iRow][col];
        MatrixInter[iRow][col]=MatrixInter[jRow][col];
        MatrixInter[jRow][col]=RowTemp[iRow][col];
    }
    return MatrixInter;
}
//Pivote Downward
double MatrixDown[9][9];
double (*(PivoteDown)(double MatrixInput[9][9],int Row,int Col,int tRow,int tCol))[9]
{
    CopyMatrix(MatrixInput,MatrixDown,Row,Col);
    Coefficient=MatrixDown[tRow][tCol];
    if(Coefficient!=1.0)
        for(col=1;col<=Col;col++)
            MatrixDown[tRow][col]/=Coefficient;
    if(tRow<Row)
        for(row=tRow+1;row<=Row;row++)
        {
            Coefficient=MatrixDown[row][tCol];
            for(col=1;col<=Col;col++)
                MatrixDown[row][col]-=Coefficient*MatrixDown[tRow][col];
        }
return MatrixDown;
}
//Pivote Upward
double MatrixUp[9][9];
double (*(PivoteUp)(double MatrixInput[9][9],int Row,int Col,int tRow,int tCol))[9]
{
    CopyMatrix(MatrixInput,MatrixUp,Row,Col);
    Coefficient=MatrixUp[tRow][tCol];
    if(Coefficient!=1.0)
        for(col=1;col<=Col;col++)
            MatrixUp[tRow][col]/=Coefficient;
    if(tRow>1)
        for(row=tRow-1;row>=1;row--)
        {
            Coefficient=MatrixUp[row][tCol];
            for(col=1;col<=Col;col++)
                MatrixUp[row][col]-=Coefficient*MatrixUp[tRow][col];
        }
    return MatrixUp;
}
//Pivote in Determinant
double MatrixPiv[9][9];
double (*(Pivote)(double MatrixInput[9][9],int Dim,int pTarget))[9]
{
    CopyMatrix(MatrixInput,MatrixPiv,Dim,Dim);
    for(row=pTarget+1;row<=Dim;row++)
    {
        Coefficient=MatrixPiv[row][pTarget]/MatrixPiv[pTarget][pTarget];
        for(col=1;col<=Dim;col++)
        {
            MatrixPiv[row][col]-=Coefficient*MatrixPiv[pTarget][col];
        }
    }
    return MatrixPiv;
}
//Determinant of Square Matrix
int dCounter,dRow;
double Det;
double MatrixDet[9][9];
double Determinant(double MatrixInput[9][9],int Dim)
{
    CopyMatrix(MatrixInput,MatrixDet,Dim,Dim);
    Det=1.0;
    if(Dim>1)
    {
        for(dRow=1;dRow<Dim;dRow++)
        {
            dCounter=dRow;
            while((MatrixDet[dRow][dRow]==0.0)&(dCounter<=Dim))
            {
                dCounter++;
                Det*=-1.0;
                CopyPointer(InterchangeRow(MatrixDet,Dim,Dim,dRow,dCounter),MatrixDet,Dim,Dim);
            }
            if(MatrixDet[dRow][dRow]==0)
            {
                Det=0.0;
                break;
            }
            else
            {
                Det*=MatrixDet[dRow][dRow];
                CopyPointer(Pivote(MatrixDet,Dim,dRow),MatrixDet,Dim,Dim);
            }
        }
        Det*=MatrixDet[Dim][Dim];
    }
    else Det=MatrixDet[1][1];
    return Det;
}
//Matrix Identity
double MatrixIdent[9][9];
double (*(Identity)(int Dim))[9]
{
    for(row=1;row<=Dim;row++)
        for(col=1;col<=Dim;col++)
            if(row==col)
                MatrixIdent[row][col]=1.0;
            else
                MatrixIdent[row][col]=0.0;
    return MatrixIdent;
}
//Join Matrix to be Augmented Matrix
double MatrixJoin[9][9];
double (*(JoinMatrix)(double MatrixA[9][9],double MatrixB[9][9],int Row,int ColA,int ColB))[9]
{
    Col=ColA+ColB;
    for(row=1;row<=Row;row++)
        for(col=1;col<=Col;col++)
            if(col<=ColA)
                MatrixJoin[row][col]=MatrixA[row][col];
            else
                MatrixJoin[row][col]=MatrixB[row][col-ColA];
    return MatrixJoin;
}
//Inverse of Matrix
double (*Pointer)[9];
double IdentMatrix[9][9];
int Counter;
double MatrixAug[9][9];
double MatrixInv[9][9];
double (*(Inverse)(double MatrixInput[9][9],int Dim))[9]
{
    Row=Dim;
    Col=Dim+Dim;
    Pointer=Identity(Dim);
    CopyPointer(Pointer,IdentMatrix,Dim,Dim);
    Pointer=JoinMatrix(MatrixInput,IdentMatrix,Dim,Dim,Dim);
    CopyPointer(Pointer,MatrixAug,Row,Col);
    for(Counter=1;Counter<=Dim;Counter++)   
    {
        Pointer=PivoteDown(MatrixAug,Row,Col,Counter,Counter);
        CopyPointer(Pointer,MatrixAug,Row,Col);
    }
    for(Counter=Dim;Counter>1;Counter--)
    {
        Pointer=PivoteUp(MatrixAug,Row,Col,Counter,Counter);
        CopyPointer(Pointer,MatrixAug,Row,Col);
    }
    for(row=1;row<=Dim;row++)
        for(col=1;col<=Dim;col++)
            MatrixInv[row][col]=MatrixAug[row][col+Dim];
    return MatrixInv;
}
//Gauss-Jordan Elemination
double MatrixGJ[9][9];
double VectorGJ[9][9];
double (*(GaussJordan)(double MatrixInput[9][9],double VectorInput[9][9],int Dim))[9]
{
    Row=Dim;
    Col=Dim+1;
    Pointer=JoinMatrix(MatrixInput,VectorInput,Dim,Dim,1);
    CopyPointer(Pointer,MatrixGJ,Row,Col);
    for(Counter=1;Counter<=Dim;Counter++)   
    {
        Pointer=PivoteDown(MatrixGJ,Row,Col,Counter,Counter);
        CopyPointer(Pointer,MatrixGJ,Row,Col);
    }
    for(Counter=Dim;Counter>1;Counter--)
    {
        Pointer=PivoteUp(MatrixGJ,Row,Col,Counter,Counter);
        CopyPointer(Pointer,MatrixGJ,Row,Col);
    }
    for(row=1;row<=Dim;row++)
        for(col=1;col<=1;col++)
            VectorGJ[row][col]=MatrixGJ[row][col+Dim];
    return VectorGJ;
}
//Generalized Gauss-Jordan Elemination
double MatrixGGJ[9][9];
double VectorGGJ[9][9];
double (*(GeneralizedGaussJordan)(double MatrixInput[9][9],double VectorInput[9][9],int Dim,int vCol))[9]
{
    Row=Dim;
    Col=Dim+vCol;
    Pointer=JoinMatrix(MatrixInput,VectorInput,Dim,Dim,vCol);
    CopyPointer(Pointer,MatrixGGJ,Row,Col);
    for(Counter=1;Counter<=Dim;Counter++)   
    {
        Pointer=PivoteDown(MatrixGGJ,Row,Col,Counter,Counter);
        CopyPointer(Pointer,MatrixGGJ,Row,Col);
    }
    for(Counter=Dim;Counter>1;Counter--)
    {
        Pointer=PivoteUp(MatrixGGJ,Row,Col,Counter,Counter);
        CopyPointer(Pointer,MatrixGGJ,Row,Col);
    }
    for(row=1;row<=Row;row++)
        for(col=1;col<=vCol;col++)
            VectorGGJ[row][col]=MatrixGGJ[row][col+Dim];
    return VectorGGJ;
}
//Matrix Sparse, Three Diagonal Non-Zero Elements
double MatrixSpa[9][9];
double (*(Sparse)(int Dimension,double FirstElement,double SecondElement,double ThirdElement))[9]
{
    MatrixSpa[1][1]=SecondElement;
    MatrixSpa[1][2]=ThirdElement;
    MatrixSpa[Dimension][Dimension-1]=FirstElement;
    MatrixSpa[Dimension][Dimension]=SecondElement;
    for(int Counter=2;Counter<Dimension;Counter++)
    {
        MatrixSpa[Counter][Counter-1]=FirstElement;
        MatrixSpa[Counter][Counter]=SecondElement;
        MatrixSpa[Counter][Counter+1]=ThirdElement;
    }
    return MatrixSpa;
}

Copy and save the above code as Matrix.h then try the following code:

#include<iostream>
#include<conio.h>
#include"Matrix.h"
int Dim;
double Matrix[9][9];
int main()
{
    cout<<"Enter your matrix dimension: ";
    cin>>Dim;
    Input(Matrix,Dim,Dim);
    cout<<"Your matrix:"<<endl;
    Output(Matrix,Dim,Dim);
    cout<<"The inverse:"<<endl;
    Output(Inverse(Matrix,Dim),Dim,Dim);
    getch();
}

Пятый урок посвящен нахождению обратной матрицы, ее свойствам, а также определению ранга матрицы

• Обратная матрица
• Ранг матрицы

Обратная матрица

Обратной матрицей A^-1 матрицы A называют матрицу, удовлетворяющую следующему равенству:

где – E это единичная матрица.

Для того, чтобы у квадратной матрицы A была обратная матрица необходимо и достаточно чтобы определитель |A| был не равен нулю. Введем понятие союзной матрицы. Союзная матрица A* строится на базе исходной A путем замены всех элементов матрицы A на их алгебраические дополнения.

Исходная матрица:

Союзная ей матрица A*:

Транспонируя матрицу A*, мы получим так называемую присоединенную матрицу A*^T:

Теперь, зная как вычислять определитель и присоединенную матрицу, мы можем определить матрицу A^-1, обратную матрице A:

➣ Численный пример

Пример вычисления обратной матрицы. Пусть дана исходная матрица A, следующего вида:

Для начала найдем определитель матрицы A:

Как видно из приведенных вычислений, определитель матрицы не равен нулю, значит у матрицы A есть обратная. Построим присоединенную матрицу, для этого вычислим алгебраические дополнения для каждого элемента матрицы A:

Союзная матрица будет иметь следующий вид:

Присоединенная матрица получается из союзной путем транспонирования:

Находим обратную матрицу:

➤ Пример на Python

Решим задачу определения обратной матрицы на Python. Для получения обратной матрицы будем использовать функцию inv():

>>> A = np.matrix('1 -3; 2 5')
>>> A_inv = np.linalg.inv(A)
>>> print(A_inv)
[[ 0.45454545 0.27272727]
 [-0.18181818 0.09090909]]

Рассмотрим свойства обратной матрицы.

Свойство 1. Обратная матрица обратной матрицы есть исходная матрица:

➤Пример на Python

>>> A = np.matrix('1. -3.; 2. 5.')
>>> A_inv = np.linalg.inv(A)
>>> A_inv_inv = np.linalg.inv(A_inv)

>>> print(A)
[[1. -3.]
 [2. 5.]]
>>> print(A_inv_inv)
[[1. -3.]
 [2. 5.]]

Свойство 2. Обратная матрица транспонированной матрицы равна транспонированной матрице от обратной матрицы:

➤ Пример на Python

>>> A = np.matrix('1. -3.; 2. 5.')
>>> L = np.linalg.inv(A.T)
>>> R = (np.linalg.inv(A)).T

>>> print(L)
[[ 0.45454545 -0.18181818]
 [ 0.27272727 0.09090909]]
>>> print(R)
[[ 0.45454545 -0.18181818]
 [ 0.27272727 0.09090909]]

Свойство 3. Обратная матрица произведения матриц равна произведению обратных матриц:

➤ Пример на Python

>>> A = np.matrix('1. -3.; 2. 5.')
>>> B = np.matrix('7. 6.; 1. 8.')

>>> L = np.linalg.inv(A.dot(B))
>>> R = np.linalg.inv(B).dot(np.linalg.inv(A))

>>> print(L)
[[ 0.09454545 0.03272727]
 [-0.03454545 0.00727273]]
>>> print(R)
[[ 0.09454545 0.03272727]
 [-0.03454545 0.00727273]]

Ранг матрицы

Ранг матрицы является еще одной важной численной характеристикой. Рангом называют максимальное число линейно независимых строк (столбцов) матрицы. Линейная независимость означает, что строки (столбцы) не могут быть линейно выражены через другие строки (столбцы). Ранг матрицы можно найти через ее миноры, он равен наибольшему порядку минора, который не равен нулю. Существование ранга у матрицы не зависит от того квадратная она или нет.

Вычислим ранг матрицы с помощью Python. Создадим единичную матрицу:

>>> m_eye = np.eye(4)
>>> print(m_eye)
[[1. 0. 0. 0.]
 [0. 1. 0. 0.]
 [0. 0. 1. 0.]
 [0. 0. 0. 1.]]

Ранг такой матрицы равен количеству ее столбцов (или строк), в нашем случае ранг будет равен четырем, для его вычисления на Python воспользуемся функцией matrix_rank():

>>> rank = np.linalg.matrix_rank(m_eye)
>>> print(rank)
4

Если мы приравняем элемент в нижнем правом углу к нулю, то ранг станет равен трем:

>>> m_eye[3][3] = 0
>>> print(m_eye)
[[1. 0. 0. 0.]
 [0. 1. 0. 0.]
 [0. 0. 1. 0.]
 [0. 0. 0. 0.]]

>>> rank = np.linalg.matrix_rank(m_eye)
>>> print(rank)
3

P.S.

Вводные уроки по “Линейной алгебре на Python” вы можете найти соответствующей странице нашего сайта. Все уроки по этой теме собраны в книге “Линейная алгебра на Python”.

Если вам интересна тема анализа данных, то мы рекомендуем ознакомиться с библиотекой Pandas.  Для начала вы можете познакомиться с вводными уроками. Все уроки по библиотеке Pandas собраны в книге “Pandas. Работа с данными”.