Загрузить PDF
Загрузить PDF
Одной из важнейших составляющих алгебры является понятие обратной функции. Обратная функции обозначается как f^-1(х) и графически представляется как отражение графика исходной функции относительно прямой у=х. В этой статье мы расскажем вам, как найти обратную функцию.
Шаги
-
1
Убедитесь, что данная функция биективна. Только биективные функции имеют обратные функции.
- Функция биективна, если она проходит тест вертикальной и горизонтальной прямыми. Проведите вертикальную прямую через график функции и подсчитайте количество раз, которое прямая пересекает график функции. Потом проведите горизонтальную прямую через график функции и подсчитайте количество раз, которое прямая пересекает график функции. Если каждая прямая пересекает график функции только один раз, то функция биективна.
- Если график не проходит тест вертикальной прямой, то он не задан функцией.
- Для алгебраического определения биективности функции подставьте f(а) и f(b) в данную функцию и определите, выполняется ли равенство a=b. В качестве примера рассмотрим функцию f(x) = 3x+5.
- f(a) = 3a + 5; f(b) = 3b + 5
- 3a + 5 = 3b + 5
- 3a = 3b
- a = b
- Таким образом, данная функция биективна.
- Функция биективна, если она проходит тест вертикальной и горизонтальной прямыми. Проведите вертикальную прямую через график функции и подсчитайте количество раз, которое прямая пересекает график функции. Потом проведите горизонтальную прямую через график функции и подсчитайте количество раз, которое прямая пересекает график функции. Если каждая прямая пересекает график функции только один раз, то функция биективна.
-
2
В данной функции поменяйте местами «х» и «у». Помните, что f(х) — другое написание «у».
- «f(x)» или «y» представляет собой функцию, а «х» — переменную. Чтобы найти обратную функцию, нужно поменять местами функцию и переменную.
- Пример: рассмотрим функцию f(x) = (4x+3)/(2x+5), которая является биективной. Поменяв местами «х» и «у», получите x = (4y + 3)/(2y + 5).
-
3
Найдите «у». Решите новое уравнение и найдите «у».
- Возможно, чтобы найти значение выражения и упростить его, вам понадобятся алгебраические приемы вроде умножения дробей или разложения на множители.
- Решение нашего примера:
- х = (4y + 3)/(2y + 5)
- х(2y + 5) = 4y + 3 — избавьтесь от дроби. Для этого умножьте обе части уравнения на знаменатель дроби (2у + 5).
- 2xy + 5x = 4y + 3 — раскройте скобки.
- 2xy — 4y = 3 — 5x — перенесите все члены с переменной (в данном случае это «у») на одну сторону уравнения.
- у (2x — 4) = 3 — 5x — вынесите «у» за скобку.
- у = (3 — 5x)/(2x — 4) — разделите обе части уравнения на (2х-4), чтобы получить окончательный ответ.
-
4
Замените «у» на f^-1(х). Это есть обратная функция для исходной функции.
- Окончательный ответ: f^-1(x) = (3 — 5x)/(2x — 4). Это обратная функция для f(х) = (4x + 3)/(2x + 5) .
Реклама
Об этой статье
Эту страницу просматривали 213 303 раза.
Была ли эта статья полезной?
Функция
принимает каждое свое значение только
при одном
значении
аргумента, поскольку линейное
уравнение
только один корень (рис.6). Значит, эта
функция имеет обратную функцию

которая определена на

так как

множеством значений функции
(рис.7). Обратная функция
произвольному числу
ставит в соответствие число

которое определяется условием
(рис.7). Выразив из этого равенства
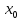
получаем
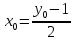
Значит, для каждого
имеем

то есть
.
Обозначив
аргумент обратной функции буквой х, а
зависимую переменную буквой

то есть, поменяв переменные местами,
получим

Итак, обратной функцией к линейной
функции
будет функция
, которая также является линейной.
Замечание.
При решении задач можно обозначать
произвольное значение аргумента обратной
функции буквой

а не

как это для ясности сделано в разобранных
примерах.
-
Пусть
обратимая функция, заданная формулой.
На основании определения обратной
функции можно сформулировать порядок
действий для нахождения функции,
обратной к функции
.
-
Теорема.
Если функция
является возрастающей (или убывающей),
то она обратима.
Пусть
для определенности функция
является возрастающей. Возьмем два
различных значения аргумента, меньшее
обозначим через

большее — через

то есть

Из этого неравенства в силу определения
возрастающей функции следует, что

а значит
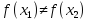
Поэтому разным значениям аргумента
соответствуют разные значения функции
и, следовательно, функция
обратима. Для убывающей функции
доказательство аналогично.
Отметим,
что любая линейная функция
обратима, если
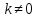
поскольку является либо возрастающей,
либо убывающей функцией, в зависимости
от знака коэффициента

Обратима также возрастающая функция

Если
функция задана формулой и нам неизвестен
ее график, то определить, будет
ли функция обратимой можно только путем
исследования количества корней уравнения

Если при некотором значении
их два или более, то функция не является
обратимой.
-
Если известен график обратимой функции, то график обратной функции можно построить путем преобразования графика функции . Следующая теорема определяет вид этого преобразования.
Теорема.
График функции
и график обратной к ней функции
симметричны
относительно прямой

Пусть
точка
с координатами
принадлежит графику функции

то есть

Тогда, по определению обратной функции

Это означает, что точка
с координатами
принадлежит графику обратной функции
(рис. 11).
Докажем,
что точки
и
симметричны относительно прямой

Для определенности рассмотрим случай,
когда точка
лежит в первом координатном угле и

Проведем через точки
и
прямые, перпендикулярные осям координат
(рис.8). Прямоугольник
является квадратом, так как имеет равные
смежные стороны:
Вершины квадрата

точки
и

имеют координаты
и
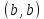
соответственно, и, значит, принадлежат
прямой
(рис.9). Поскольку диагонали квадрата
перпендикулярны и делятся точкой
пересечения пополам, то точки
и
симметричны относительно диагонали

а, следовательно, и относительно прямой

Таким
образом, мы доказали, что точка плоскости,
симметричная точке графика функции
относительно прямой

принадлежат графику обратной функции

Аналогично доказывается, что верно и
обратное утверждение: точка, симметричная
точке графика обратной функции
относительно прямой

принадлежат графику функции
Значит, графики этих функций симметричны.
Теорема доказана.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Обратная функция
Что такое обратная функция? Как найти функцию, обратную данной?
Определение.
Пусть функция y=f(x) определена на множестве D, а E — множество её значений. Обратная функция по отношению к функции y=f(x) — это функция x=g(y), которая определена на множестве E и каждому y∈E ставит в соответствие такое значение x∈D, что f(x)=y.
Таким образом, область определения функции y=f(x) является областью значений обратной к ней функции, а область значений y=f(x) — областью определения обратной функции.
Чтобы найти функцию, обратную данной функции y=f(x), надо:
1) В формулу функции вместо y подставить x, вместо x — y:
x=f(y).
2) Из полученного равенства выразить y через x:
y=g(x).
Пример.
Найти функцию, обратную функции y=2x-6.
1) x=2y-6
2) -2y=-x-6
y=0,5x+3.
Функции y=2x-6 и y=0,5x+3 являются взаимно обратными.
Графики прямой и обратной функций симметричны относительно прямой y=x (биссектрисы I и III координатных четвертей).
y=2x-6 и y=0,5x+3 — линейные функции. Графиком линейной функции является прямая. Для построения прямой берём две точки.

Теорема (необходимое и достаточное условие обратимости функции)
Если функция y=f(x) определена и непрерывна на числовом промежутке, то для обратимости функции необходимо и достаточно, чтобы f(x) была строго монотонна.
Причем, если y=f(x) возрастает на промежутке, то и обратная к ней функция также возрастает на этом промежутке; если y=f(x) убывает, то и обратная функция убывает.
Если условие обратимости не выполнено на всей области определения, можно выделить промежуток, где функция только возрастает либо только убывает, и на этом промежутке найти функцию, обратную данной.
Классический пример — функция y=x². На промежутке [0;∞) функция возрастает. Условие обратимости выполнено, следовательно, можем искать обратную функцию.
Так как область определения функции y=x² — промежуток [0;∞), область значений на этом промежутке — также [0;∞), то область определения и область значений обратной функции — также [0;∞).
1) x=y².
2)
Так как y≥0, то
то есть на промежутке [0;∞) y=√x — функция, обратная к функции y=x². Их графики симметричны относительно биссектрисы I и III координатных четвертей:
В алгебре наиболее известными примерами взаимно обратных функций являются показательная и логарифмическая функция, а также тригонометрические и обратные тригонометрические функции.








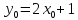





 .
.



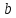
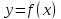

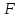


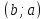







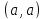




![Rendered by QuickLaTeX.com [begin{array}{l} y = 2x - 6\ begin{array}{*{20}{c}} x&vline& 0&vline& 3\ hline y&vline& { - 6}&vline& 0 end{array} end{array}]](https://www.algebraclass.ru/wp-content/ql-cache/quicklatex.com-d7fa80623853e96d4e8f32fe255e4c99_l3.png)
![Rendered by QuickLaTeX.com [begin{array}{l} y = 0,5x + 3\ begin{array}{*{20}{c}} x&vline& 0&vline& { - 6}\ hline y&vline& 3&vline& 0 end{array} end{array}]](https://www.algebraclass.ru/wp-content/ql-cache/quicklatex.com-c9a8b5feb781d3c105f0903d50e2b586_l3.png)
