Область определения функции: понятие
Функция задается тогда, когда любому значению, например x соответствует любое значение y. Независимой переменной называют значение х или по другому — аргументом. Числовое значение y, как правило, является зависимой переменной.
Данная зависимость между x и y в алгебре называют функциональной. Записывают ее в виде функции y = f(x)
Другими словами, функция, это когда значения одной переменной зависят от значений другой переменной.
Далее можно сформулировать определение область функции. То есть, на какой промежуток действе функции распространяется.
Определение
В математике под областью определения функции понимают множество, которое включает в себя все значения аргумента. Если функция имеет предел, то он является значением аргумента при котором функция возрастает или убывает. Область определения функции также называется областью допустимых значений функции.
Область функции можно выразить геометрически. Например, в виде графика. Где за основу берутся оси х и y.
Ограничение области определения
Область ограничения действительных чисел может быть от [(0 ;+infty)].
Например: [-4;1)U[5,7).
Область определения может указывать на следующие характеристики:
- деление функции как [y=x+frac{2 cdot x}{x^{4}-1}];
- корень четной степени и переменная под корнем:
[=sqrt{x+1} text { или } y=sqrt[n]{2^{2 cdot x+1}}]
- переменная в основании степенного значения
- логарифмическая переменная [y=ln frac{x^{4}+x}{8} ; y=2+]. Значения основания должно быть положительным. Также, как и логарифмическое значение.
- переменная тангенса и котангенса в виде следующего уравнения: y=arcsin (x+4)+4*x2.
Если отсутствует хотя бы один из перечисленных характеристик область определения функции определяется иначе.
Пример 1: [y=frac{x^{4}+2 x-x+2}{4}+2 frac{2}{3} cdot x], в данном множестве нет переменной, поэтому и решается оно иначе.
Пример 2: [y=frac{3}{x-1}], нужно вычислить область определения. Обязательно, при решении нужно уделить внимание на знаменатель. Потому что, по законам алгебры деление на ноль запрещено.
Получаем следующее действие:[frac{3}{x-1}].
Область значения не должна быть равной единице, так как в знаменателе получим нулевое значение. Отсюда область определения будет в пределах [(-infty, 1) cup(1,+infty)].
Область определения для суммы, разности и произведений числовых значений
Чтобы правильно уметь определять данную область, нужно знать следующие утверждения: если функция вычисляется, при помощи суммы: [f_{1}+f_{2}+ldots f_{n} text { или } mathrm{y}=f_{1}+f_{2}+ldots f_{n}]
Область определения будет следующего вида: [mathrm{D}(mathrm{f})=mathrm{D}left(f_{1}right)left(f_{2}right) ldotsleft(f_{n}right)]
Пример суммы числовых значений: возьмем уравнение: [y=x^{7}+x+5+t g x].
Решение: уравнение представлено в виде суммы нескольких значений, где степень равна семи, показатель один.
Области определения tg характерны все действительные числа.
Ответ: для заданной функции относится пересечение областей или количество действительных чисел кроме [pi / 2+pi cdot n cdot n in z]
Пример разности значений:
Пример произведения чисел:
Сложные функции х и y и их область определения и значения
Сложная функция имеет следующий вид: [mathrm{y}=f_{1}left(f_{2}(mathrm{k})right)]
D (f) — множество значений;
Пересечение двух множеств и будет являться областью определения функции сложного типа.
[mathrm{k} in Dleft(f_{2}right) text {и } D f_{2}(x) in Dleft(f_{1}right)]
Примеры:
[y=ln x^{2}]
Представим функцию в виде: [mathrm{y}=f_{1}left(f_{2}(mathrm{k})right)]
Используем изученные в данном уроке области определения:
Исходя из этого получаем систему неравенства:
Ответ: все действительные числа, кроме нуля.
Область определения функции в виде дробного значения
Когда функция задается выражение в виде дроби. Переменная значений находится в знаменателе. Следовательно, область определения являются действительные числа. Исключением служит число, которое приведет знаменатель к нулевому значению.
Пример №1: [y=frac{x-4}{x+4}]. Решив уравнение, определим искомое значение области определения. Которое является [-infty ;-4 cup-4 ;+infty]
Пример №2: [y=frac{1}{x^{2-1}}];
[x^{2-} 1=0 Rightarrow x^{2} Rightarrow x_{1}=-1 quad x_{2}=1]
Искомая область: [-]-infty ;-1[cup]-1 ; 1[cup] 1 ;+infty[.]
Пример №3. [y=cos x+frac{3}{x^{2}-4}].
Первое слагаемое имеет область определения множество действительных чисел. Второе — также все числа, кроме -2 и 2, они приведут знаменатель к нулю. Область определения должна соответствовать условиям двух слагаемых и равняться действительным числам, кроме -2 и 2.
Область определения тригонометрических функций
Множество значений всех действительных чисел, будет являться областью определения функций синус и косинус, и записываться следующим образом.
Функции являются ограниченными, как сверху, так и снизу, y = sin x и y = cos x. Промежуток их действия сводится к неравенству -1 ≤ y ≤ 1
Областью определения функции тангенс tg x, является выражение [mathrm{x} neq frac{pi}{2}+pi k, mathrm{k} in z].
Областью определения функции y = ctg x является множество чисел [x neq frac{pi}{2}, quad k in z].
На нижеприведенных примерах подробно расписано решение задач, при определении области функции, при заданных промежутках значений.
Пример №1
Определить область значения функции sin x
Данный вид функции относится к категории периодической. Ее период равняется 2п.
Определяем множество значений на следующем отрезке:( 0;2).
Пример №2:
Необходимо определить область значения функции cos x.
Наименьшее значение равно -1;
Минимальное значение косинуса равняется -1, потому что наименьшее значение х, на окружности стремится к этому значению и следовательно равняется -1.
Максимальное значение косинуса будет соответственно 1. Поскольку значение на окружности х имеет число 1.
Область значение, следовательно, будет от минус одно до плюс одного. [-1;1].
Применяем двойное неравенство и записывает следующее выражение:
[-1 leq cos x leq 1]
Область значения косинуса никогда не зависит от аргумента, только если сам аргумент выражен в виде сложного выражения. Где имеют место ограничения касающиеся области определения и области значения.
Таким образом, минимальное значение cos x, cos (15a), cos(5-11x) и так далее, будет однозначно равняться -1;
Самым максимальным значением cos x, cos(4φ), cos(5х+3) равняется 1.
Область значений функции y=cos x — также промежуток [-1;1].
Область значения квадрата косинуса, будет промежуток от нуля до единицы[0;1]. Потому что число в четной степени, является не отрицательным.
Аналогичным образом находим область значений модуля косинуса — промежуток [0;1]
[0 leq(cos a) leq 1]
Пример №3
y = tgx на определенном интервале [left(-frac{pi}{2} ; frac{pi}{2}right)]
Решение:
Из правил алгебры, известно, что производная тангенса имеет положительное значение. Соответственно функция будет иметь возрастающую характеристику.
Далее необходимо определить поведение функции, в заданных пределах.
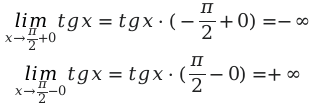
Выполнив решение, мы получаем рост значений от минус до плюс бесконечности. Решение будет сводиться к следующему: множество решение заданной функции, будет множество всех действий функции.
Пример №4
[y=(arcsin x)=frac{1}{sqrt{1-x^{2}}}] на определенном интервале (-1;1).
Решение:
Для всех значений x производная будет положительной, в пределах от -1;1
Нет времени решать самому?
Наши эксперты помогут!
Область определения показательной и логарифмической функции
Показательная функция записывается как: y = kx, где значения:
- x — показатель степени;
- k — число, которое обязательно больше нуля и не равно единице.
Определение
Область определения показательной функции — это множество значений R.
Основные примеры показательных функций:
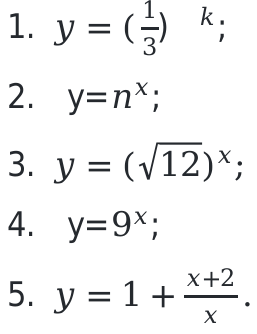
Область определения, для этих функций, записывается следующим образом: [(-infty,+infty)].
Логарифмическая функция выражается как: y=log nk
Где значение n, имеет значение больше нуля и не менее единицы.
Определение
Область определения логарифма и логарифмической функции — это множество положительных значений и действительных чисел.
Рассмотрим на примере, характер решения задачи данной функции.
Пример №1:
y = lnx , определить область определения натурального логарифма.
[D(y)=(0 ;+infty)]
На заданном интервале, производная будет иметь положительное значение, и функция будет возрастать на всем промежутке.
[y=ln x=frac{1}{x}]
Определим односторонний предел при, стремлении аргумента к нулю и когда значение x стремится к бесконечности.
Из данного решения мы видим, что значения будут возрастать от минус бесконечности до плюс бесконечности.
Из этого следует, что множество всех действительных чисел – является областью значений функции натурального логарифма ln.
Ответ: множество всех действительных чисел, это и есть область значений функции ln.
Определения области значения функции x
На примерах рассмотрим, как определить области значений функции.
Первоначально, необходимо определить значения непрерывной функции y=f(x).
Известно, что функция непрерывная и достигает своих максимальных max f(x) и минимальных min f(x) значений, на разных периодах. Из этого следует отрезок, где находятся значения исходной функции. Тогда решение состоит в нахождении точек максимума и минимума.
Пример №1 :
Необходимо вычислить область значений уравнения y = x4 — 5x3 + 6x2 на отрезке [ 1 ; 4 ] [1; 4].
Для решения задачи необходимо произвести следующие действия:
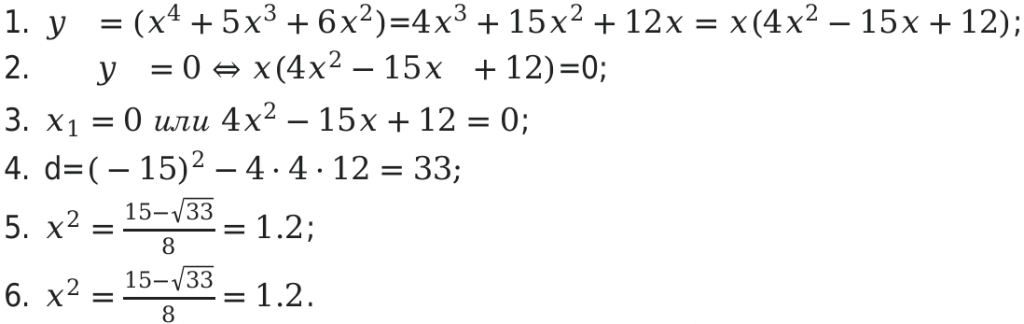
Следующим шагом будет определение значений функции в конечной и начальной точках.
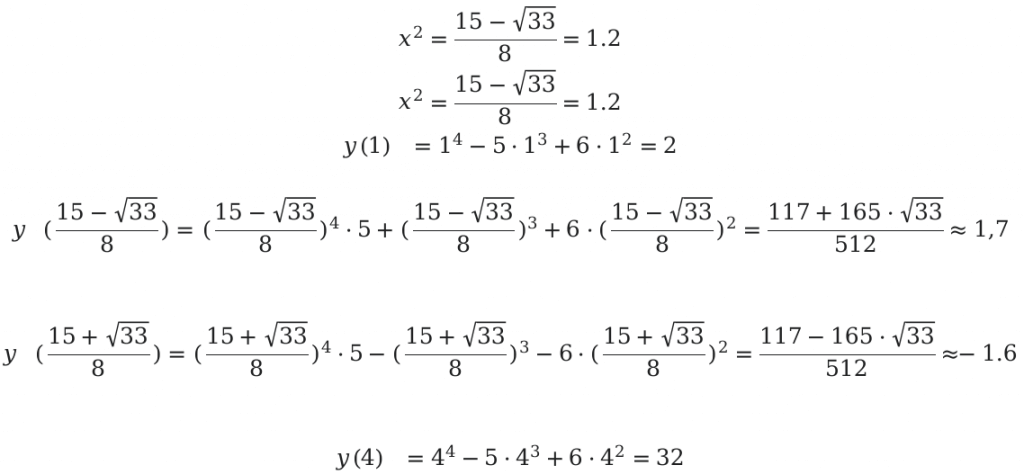
Ответ: [left(frac{117-165 cdot sqrt{33}}{512} ; 32right)]
Пример №2.
Необходимо вычислить область значений уравнения
y = x4 — 7x3 + 5x2 на отрезке [ 1 ; 4 ] [1; 4].
Для решения задачи необходимо произвести следующие действия:
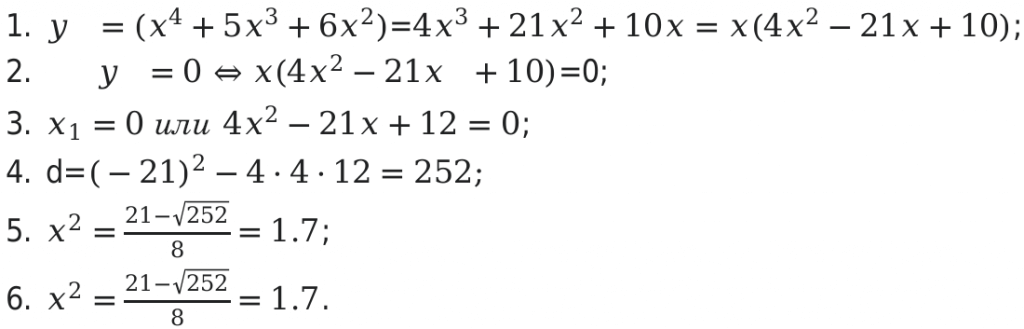
Следующим шагом будет определение значений функции в конечной и начальной точках.
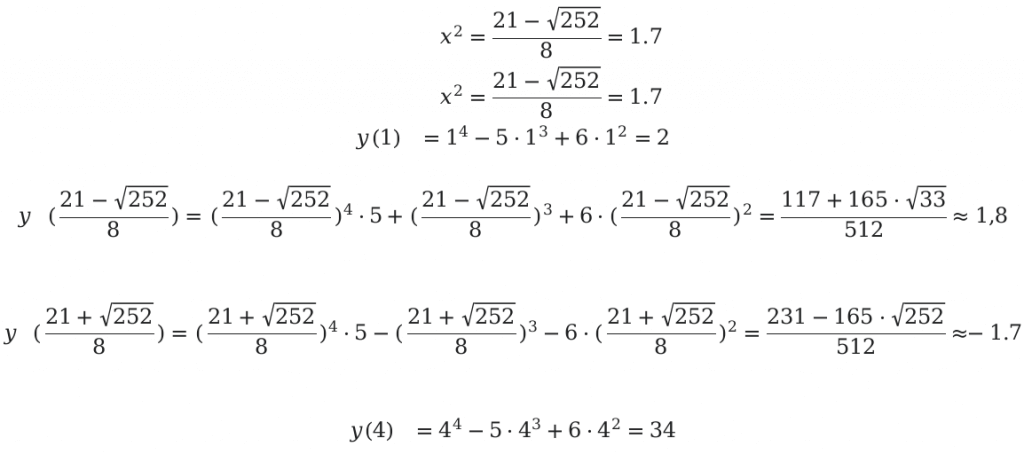
Ответ: [left(frac{231-165 cdot sqrt{33}}{512} ; 34right)]
Пример №3 :
На этом примере подробно рассмотрим, как вычисляются значения непрерывной функции y= f(x), в определенных промежутках.
Для этого, первоначально вычислим:
- наименьшее и наибольшее значение;
- определим промежуток возрастания и убывания функции;
- односторонние пределы;
- предел бесконечности.
Решение:
Для решения возьмем функцию [y=frac{1}{x^{2}-4}] и вычислим область значений на промежутке (-2;2).
Находим наименьшее и наибольшее значение функции на заданном отрезке.
Из данных вычислений видно, что максимальное значение равно 0, так как в этой точке происходит перемена знака функции и соответственно функция начинает убывать.
А именно: [y(0)=frac{1}{0^{2}-4}=-frac{1}{4}]
[-frac{1}{4}] — будет являться наибольшим значение заданной функции.
Следующим шагом в нашем решении, будет выяснение направления функции. Когда x значение стремится к (-2) и (+2).
В алгебре иными словами эти значения называют односторонними пределами.
Решение выглядит следующим образом.
В конечном итоге мы получаем, что в пределах от -2 до 0, функции будут возрастать [text { От }-infty text { до }-frac{1}{4} text {. }]
Если аргумент меняется, от 0 до то наоборот будет убывать к [-infty].
Следовательно, необходимое множество значений будет на интервале [-infty text { до }-frac{1}{4}].
Ответ: [left(-infty-frac{1}{4}right)]
Область определения функции y
Пример №1:
Данная функция имеет определенное значение, только при положительных значениях. [D(y)=(0 ;+infty)].
Производная будет иметь следующий вид: [y=(ln x)=frac{1}{x}].
Так как функция имеет положительное значение, то на всем промежутке будет наблюдаться ее возрастание. От [-infty text { до + — }].
Поэтому область значения — это множество всех натуральных значений.
Пример №2:
У функции [y=frac{9}{z^{2}-1}];
Если значение z имеет положительное значение, то функция будет считаться определенной.
Вычислим наибольшее и наименьшее значение, а также промежутки возрастания и убывания.
Если значение x будет больше, либо равным 0,то функция будет убывать.
Если значение x будет меньше либо равным нулю , функция будет возрастать.
Затем рассмотрим поведение функции и ее значения на бесконечной прямой.
Вывод: если аргумент изменяется от [-infty] до 0, тогда значение функции увеличиваются от 0 до 9 . Когда значения аргумента меняются от 0 до [+infty], значения функции будут уменьшаться от 9 до 0.
Пример №3:
Определить область значений [y=frac{x}{x-2}];
По правилам математики, знаменатель не может равняться нулю. Поэтому: [D(y)=(-infty ; 2)(+infty ; 2)].
Определим множества на первом отрезке. [(-infty ; 2)]. На этом отрезке функция будет убывающей и значение отрицательным:
Функция ассиметрично начнет приближаться к 1, когда аргумент будет изменяться к минус бесконечности.
Определим множества на втором отрезке [(+infty ; 2)].
На этом отрезке функция будет также убывающей:
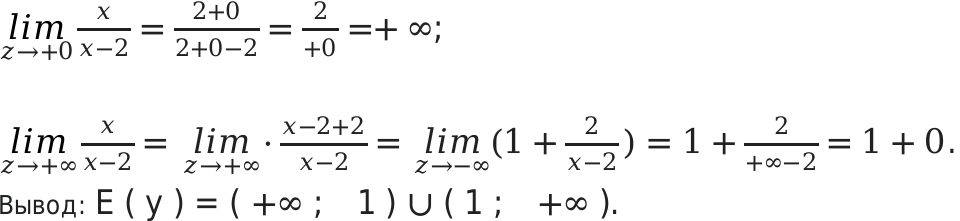
ДЕЙСТВИТЕЛЬНЫЕ
ФУНКЦИИ ДЕЙСТВИТЕЛЬНОЙ ПЕРЕМЕННОЙ
2.1. Функция. Основные понятия, связанные с определением функции
Одним
из основных математических понятий
является понятие функции. Понятие
функции связано с установлением
зависимости (связи) между элементами
двух множеств.
Пусть
даны два непустых множества X
и Y.
Соответствие f,
которое каждому элементу x
X сопоставляет один и
только один элемент у
Y,
называется функцией и записывается у
= f(x),
x
X или f
: X
Y.
Говорят
еще, что функция f
отображает множество X
на множество Y.
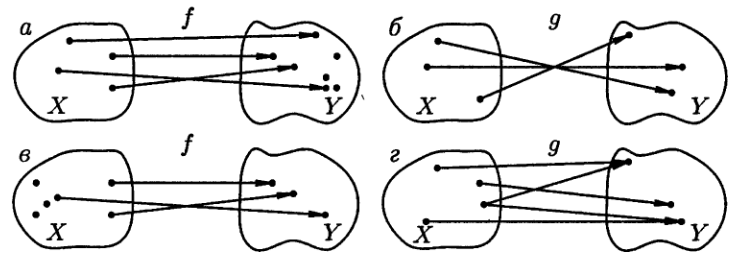
Рис. 1.
Например, соответствия f
и g, изображенные на
рисунке 1 а и б, являются функциями,
а на рисунке 1 в и г — нет. В случае
в — не каждому элементу xX
соответствует элемент уY.
В случае г не соблюдается условие
однозначности.
Отношение R называется функциональным,
если из
u
следует.
Функциональное отношение называется
функцией.
Определение
1. Пусть
и
– произвольные множества действительных
чисел. Если на множестве
задано отображение
,
при котором каждому
соответствует действительное число
,
то говорят, что на множестве
определена действительная
функция
действительной переменной
.
Множество
называется областью
определения, а множество
– множеством значений
числовой функции
.
Определим
арифметические операции над функциями.
Определение
2. Пусть функции
и
определены на множестве
.
Суммой
называют функцию, значение которой для
каждого
равно сумме значений функций
и
для этого значения
:
.
Аналогично вводится
понятие разности
функций:
.
Произведением
функций
и
называют такую функцию
на множестве
,
что
.
Если
функция
задана на множестве
и не обращается на нем в нуль, то через
обозначают такую функцию на
,
что
.
Функцию
называют частным
функций
и
и обозначают
.
Таким образом,
.
Понятия
суммы, разности, произведения и частного
функций применяют и в том случае, когда
данные функции имеют различную область
определения. В этом случае их рассматривают
на пересечении областей определения.
Пример
1. Пусть функция
ставит в соответствие каждому числу
из отрезка
число
,
а функция
ставит в соответствие каждому числу
из отрезка
число
.
Найдем сумму этих функций.
Решение.
Имеем
.
Функция
ставит в соответствие каждому числу
число
.
Задать функцию – значит указать закон,
по которому каждому значению аргумента
из области определения ставится в
соответствие значение зависимой
переменной из области значений функции.
Наиболее
часто используются три способа задания
функции: аналитический, табличный и
графический. Аналитический состоит в
том, что с помощью формулы устанавливается
алгоритм вычисления значения функции
для каждого из значений аргумента
,
областью определения функции в этом
случае считается множество значений
аргумента, при которых данная формула
имеет смысл.
Пример 2. Найти область определения
функции

Решение.
Это выражение имеет
числовое значение, если
,
и
.
Иными словами, для нахождения области
определения надо исключить из
корни уравнений
,
и
.
Решая эти уравнения, получаем корни:
-2, 8, 1, 2 и записываем область определения
данной функции
.
В некоторых случаях функция задается
на различных числовых множествах разными
выражениями, например
или (функция Дирихле)
На
практике часто удобным оказывается
табличный способ задания функций,
например, при экспериментальных
измерениях, социологических опросах,
при составлении отчетов банковской
деятельности и т.д. На табличном способе
задания, хранения и обработки информации
основаны базы данных. В общем случае
таблица имеет вид (табл. 1):
Таблица 1
|
|
|
|
|
|
|
|
|
|
|
|
Она
позволяет находить значения функции
для выбранных значений аргумента. Таким
образом, таблица не задает функции,
поскольку для задания функции надо
знать ее значения для всех
,
а не только для некоторых. Существуют
методы, позволяющие по такой таблице
подбирать выражение
,
разумеется, с определенной точностью.
При графическом способе соответствие
между аргументом и функцией задается
посредством графика.
Определение
3. Графиком
функции
называется множество пар
.
Каждая
пара
состоит из двух чисел, а потому может
быть изображена точкой
на координатной плоскости. Следовательно,
график числовой функции может быть
наглядно изображен множеством точек
координатной плоскости.
Обычно
графиком функции является некоторая
линия. Однако, не всякое множество точек
плоскости является графиком некоторой
функции. Из определения функции следует,
что каждому значению
соответствует только одно значение
,
а потому прямая, параллельная оси
ординат, может пересекать график функции
не более чем в одной точке. Например,
окружность не является графиком
какой-либо функции, так как прямые,
параллельные оси ординат, могут пересекать
ее в двух точках; полуокружность на рис.
2, а
является графиком функции
,
а полуокружность на рис. 2, б
– графиком функции
.
Рис. 2
На практике строят не графики функций,
а эскизы таких графиков. Для этого обычно
составляют таблицу значений функции
для некоторых значений аргумента,
наносят на плоскость соответствующие
точки и соединяют их линией. При этом
предполагается, что график функции
является достаточно плавной линией, а
найденные точки достаточно точно
показывают ход изменения функции. Если
эти предположения не выполняются, то
построенный график будет сильно
отличаться от истинного.
Пример
3. Построим график
функции
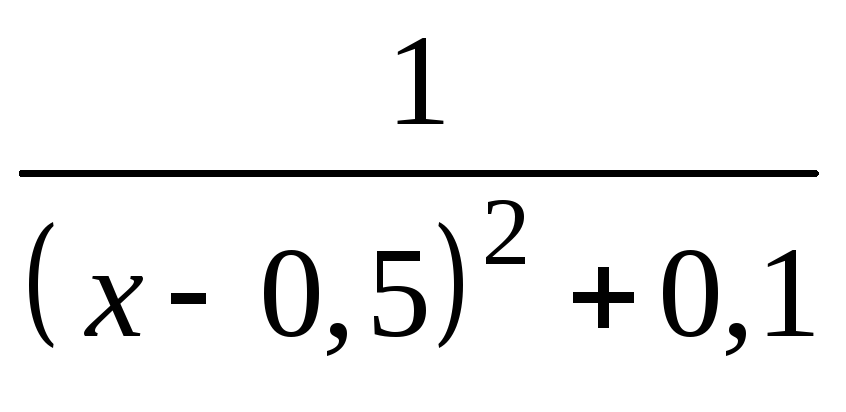
Решение.
Составляем таблицу
значений функции для
с шагом 1 (табл.2)
Таблица 2
|
|
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
4 |
|
|
0,10 |
0,16 |
0,42 |
2,86 |
2,86 |
0,42 |
0,16 |
0,10 |
Н
аносим
полученные точки на плоскость и соединяем
их плавной непрерывной линией. Получаем
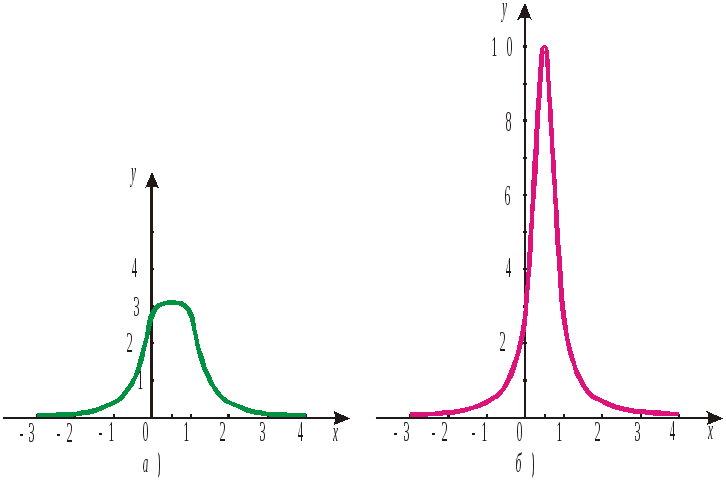
график, изображенный на рис. 3, а.
Заметим, что этот график значительно
отличается от истинного (рис. 3, б)
в связи с большим значением шага таблицы.
Рис. 3
Не всякий
график изображается непрерывной линией,
например график функции
имеет один
разрыв (рис. 4), а график функции
— целая часть числа
– имеет бесконечное число разрывов
(рис. 5).
Рис. 4 Рис. 5
Встречаются
функции, графики которых невозможно
изобразить. Примером такой функции
является функция Дирихле, определенная
выше. Так как на сколь угодно малом
отрезке числовой прямой имеются как
рациональные, так и иррациональные
точки, то график функции Дирихле не
является линией. Он состоит из точек
оси абсцисс с иррациональными абсциссами
и точек прямой
с рациональными абсциссами. Построить
такой график невозможно.
Пусть
известны графики заданных на
функций
и
.
Чтобы построить график функции
,
достаточно для каждого
сложить ординаты графиков этих функций.
Чтобы построить график функции
,
достаточно для каждого
перемножить ординаты графиков функций
и
.
При этом
обращается в нуль, если хотя бы одна из
функций
,
обращается в нуль в данной точке. График
функции
строят, деля
на ординаты графика функции
.
При этом в точках, где
обращается в нуль, функция
не определена. Обычно около этих точек
график функции
неограниченно удаляется от оси абсцисс.
Пример
4. Построим график
функции
.
Решение.
Строим график функции
.
Прибавляя 1 к ординатам этого графика,
получаем график функции
.
Выполняя деление числа 6 на ординаты
последнего графика, получаем ординаты
графика функции
.
Перемножая найденные ординаты и ординаты
графика функции
,
получаем искомый график. На рис. 6
изображено последовательное построение
графика функции
.
Рис. 6
На
практике применяются приборы, автоматически
записывающие ход изменения некоторых
величин с течением времени (осциллографы,
термографы, сейсмографы и т.д.). Они
задают графики этих величин как функции
времени. Следует иметь в виду, однако,
что это задание является лишь приближенным,
так как получающаяся линия имеет
некоторую толщину, и потому значение
,
соответствующее данному значению
,
определяется по графику лишь приближенно.
Определение
4. Пусть числовая функция
задана на множестве
,
а функция
– на множестве
,
и пусть
.
Тогда существует отображение
множества
в
,
задаваемое формулой
.
Это отображение является числовой
функцией, заданной на множестве
,
и называется суперпозицией
(композицией)
функций или сложной
функцией.
Для
математического анализа наиболее
существенным является случай, когда
функции
и
заданы своими выражениями
и
.
В этом случае выражение функции
получается следующим образом: в выражении
каждое вхождение буквы
заменяется выражением
.
Пример
5. Найдем выражение для
суперпозиций
и
,
где
,
.
Решение.
Заменяя в выражении
каждое вхождение буквы
на
,
получаем выражение
для функции
.
Таким же образом получаем выражение
для функции
.
Может
случиться, что множество значений
выражения, задающего функцию
,
не является подмножеством области
определения
функции
.
Тогда выражение, полученное подстановкой
выражения для
в выражение для
,
определяет функцию
лишь для тех
,
при которых
.
Пример 6.
Найдем область определения функции
,
если
,
.
Решение. Так как
имеет значение лишь при
,
то искомая область определения функции
задается неравенством
.
Из него находим, что
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Вспомним кратко основные определения функции в математике.
Функция — это зависимость переменной « y » от
независимой переменной « x ».
Функцию можно задать через формулу (аналитически). Например:
у = 2x
- « x » называют независимым аргументом функции;
- « y » зависимой переменной или значением функции.
Вместо « x » (аргумента функции) в формулу «у = 2x» подставляем произвольные числовые значения
и по заданной формуле вычисляем
значение « y ».
Подставим несколько числовых значений вместо « x » в формулу «у = 2x» и запишем результаты в таблицу.
| x | y = 2x | ||||||
|---|---|---|---|---|---|---|---|
| x = −2 | у = 2 · (−2) = −4 | ||||||
| x = 0 | y = 2 · 0 = 0 | ||||||
x =
|
y = 2 ·
= 1 |
||||||
| x = 3 | y = 2 · 3 = 6 |
Запомните!
Область определения функции — это множество числовых значений, которые можно подставить вместо « x » (аргумента функции).
Обозначают область определения функции как:
D(y)
Вернемся к нашей функции «у = 2x» и найдем её область определения.
Посмотрим ещё раз на таблицу функции «y = 2x», где
мы подставляли произвольные числа вместо « x », чтобы найти « y ».
| x | y = 2x | ||
|---|---|---|---|
| −2 | −4 | ||
| 0 | 0 | ||
|
1 | ||
| 3 | 6 |
Так как у нас не было никаких ограничений на числа, которые можно подставить вместо « x », можно утверждать,
что вместо « x » мы могли подставлять любое действительное число.
Другими словами, вместо « x » можно подставить любые числа, например:
- −2
- 0
- 10
- 30,5
- 1 000 000
- и так далее…
Запомните!
Областью определения функции называют множество чисел,
которые можно подставить вместо « x ».
В нашей функции «у = 2x» вместо « x »
можно подставить любое число, поэтому область определения функции «у = 2x» — это любые действительные числа.
Запишем область определения функции «у = 2x» через математические обозначения.
у = 2x
D(y): x — любое действительное число
Ответ выше написан словами без использования специального математического языка. Заменим лишние слова на
математические символы.
Для этого вспомним понятие числовой оси.
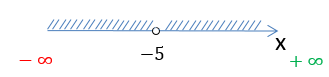
Заштрихуем область на числовой оси, откуда можно брать значения для « x » в функции «у = 2x».
Так как в функции
«у = 2x» нет ограничений для « x »,
заштрихуем всю числовую ось от минус бесконечности «−∞» до плюс бесконечности
«+∞».
Запишем результат по правилам записи неравенств.
D(y): x ∈ (−∞ ; +∞)
Запись выше читается как: « x » принадлежит промежутку от минус бесконечности
до плюс бесконечности.
Запишем окончательный ответ для области определения функции.
Ответ:
D(y): x ∈ (−∞ ; +∞)
По-другому промежуток
« x ∈ (−∞ ; +∞) » можно записать
как
«x ∈ R».
Читается «x ∈ R» как: « x » принадлежит всем действительным числам».
Записи « x ∈ (−∞ ; +∞) » и
«x ∈ R» одинаковы по своей сути.
Область определения функции с дробью
Разберем пример сложнее, когда в задании на поиск области определения функции есть дробь с « x » в знаменателе.
Разбор примера
Найдите область определения функции:
Задание «Найдите область определения функции» означает, что нам нужно определить все числовые значения, которые может принимать « x »
в функции
« f(x) = ».
По законам математики из школьного курса мы помним, что на ноль делить нельзя.
Иначе говоря,
знаменатель (нижняя часть дроби) не может быть равен нулю.
Переменная « x » находится в знаменателе функции «f(x) = ».
Так как на ноль делить нельзя, запишем, что знаменатель не равен нулю.
x + 5 ≠ 0
Решим полученное линейное уравнение.
Получается, что « x » может принимать любые числовые значения кроме «−5».
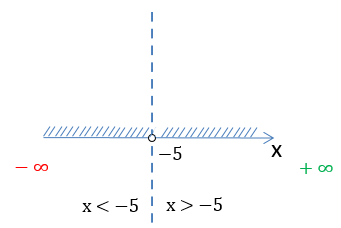
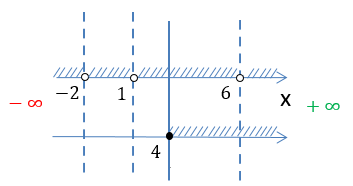
На числовой оси заштрихуем все доступные значения для « x ».
Число «−5» отмечено
«пустой»
точкой на числовой оси, так как не входит в область допустимых значений.
Запишем заштрихованную область на числовой оси через знаки неравенства.
Запишем промежутки через математические символы. Так как число «−5» не входит
в область определения функции, при записи ответа рядом с ним будет стоять
круглая скобка.
Вспомнить запись ответа через математические символы можно в уроке
«Как записать ответ неравенства».
x ∈ (−∞ ; −5) ∪ (−5 ; +∞)
Запишем окончательный ответ для области определения функции
«f(x) = ».
Ответ:
D(y): x ∈ (−∞ ; −5) ∪ (−5 ; +∞)
Область определения функции с корнем
Рассмотрим другой пример. Требуется определить область определения функции, в которой содержится квадратный корень.
Разбор примера
Найти область определения функции:
y = √6 − x
Из урока «Квадратный корень» мы помним,
что подкоренное выражение корня чётной степени должно быть больше или равно нулю.
Найдём, какие значения может принимать « x » в функции
«у = √6 − x».
Подкоренное выражение
«6 − x» должно быть больше или равно нулю.
6 − x ≥ 0
Решим линейное неравенство по правилам урока «Решение линейных неравенств».
6 − x ≥ 0
−x ≥ −6 | ·(−1)
x ≤ 6
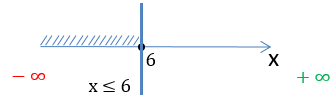
Запишем полученный ответ, используя числовую ось и математические символы. Число «6» отмечено
«заполненной»
точкой на числовой оси, так как входит в область допустимых значений.
x ∈ (−∞ ; 6]
Запишем окончательный ответ для области определения функции
«y = √6 − x» .
Так как число «6» входит
в область определения функции, при записи ответа рядом с ним будет стоять
квадратная скобка.
Ответ:
D(y): x ∈ (−∞ ; 6]
Правило для определения области определения функции
Запомните!
Чтобы найти область определения функции нужно проверить формулу функции по двум законам школьного курса математики:
- на ноль делить нельзя (другими словами, знаменатели дробей с « x » не должны быть равны нулю);
- подкоренные выражения корней чётной степени должны быть больше или равны нулю.
При нахождении области определения функции необходимо всегда задавать себе два вопроса:
- есть ли в функции дроби со знаменателем, в котором есть « x »?
- есть ли корни четной
степени с « x »?
Если на оба вопроса вы получаете отрицательный ответ, то область определения функции — это все действительные числа.
Рассмотрим пример поиска области определения функции с корнем и дробью.
Разбор примера
Найдите область определения функции:
Идем по алгоритму. Задаём себе первый вопрос, есть ли в функции дробь с « x » в знаменателе. Ответ: да, есть.
В функции «
f(x) = √x + 3 +
»
есть дробь «
»,
где « x » расположен в знаменателе. Запишем условие, что знаменатель
« x 2 − 9 »
не может быть равен нулю.
Решаем квадратное уравнение через
формулу квадратного уравнения.
x1;2 =
x2 − 9 ≠ 0
x1;2 =
| −0 ± √02 − 4 · 1 · (−9) |
| 2 · 1 |
x1;2 ≠
x1;2 ≠
x1;2 ≠
x1;2 ≠ ±3
Запомним полученный результат. Задаем себе
второй
вопрос.
Проверяем, есть ли в формуле функции
«
f(x) = √x + 3 +
»
корень четной степени.
В формуле есть квадратный корень «
√x + 3
».
Подкоренное выражение «x + 3»
должно быть больше или равно нулю.
x + 3 ≥ 0
Решим линейное неравенство.
x + 3 ≥ 0
x ≥ −3
Объединим полученные ответы по обоим вопросам:
- знаменатель дроби
«
» не равен нулю ; - подкоренное выражение «
√x + 3
» должно быть больше или равно нулю.
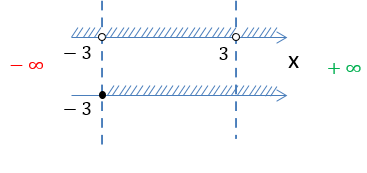
Объединим все полученные результаты на числовых осях.
Сравнивая полученные множества, выберем только те промежутки, которые удовлетворяют обоим условиям.
Выделим красным заштрихованные промежутки, которые совпадают на обеих числовых осях.
Обратим внимание, что числа «−3» и «3» отмечены «пустыми» точками и не входят в итоговое решение.
Получаем два числовых
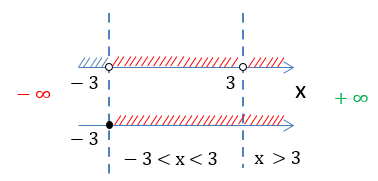
промежутка «−3 < x < 3» и «x > 3», которые являются областью определения функции
«f(x) = √x + 3 + ».
Запишем окончательный ответ.
Ответ:
D(y): x ∈ (−3 ; 3) ∪ (3 ; +∞)
Примеры определения области определения функции
Разбор примера
Найти область определения функции:
y = 6√x +
5√1 + x
Для поиска области определения функций задаем себе
первый вопрос.
Есть ли знаменатель, в котором содержится « x »?
Ответ: в формуле функции
«y = 6√x +
5√1 + x»
нет дробей.
Задаем
второй вопрос.
Есть ли в функции корни четной степени?
Ответ: в функции есть корень шестой степени:
«6√x».
Степень корня — число «6». Число «6» — чётное,
поэтому подкоренное выражение корня «6√x»
должно быть больше или равно нулю.
x ≥ 0
В формуле функции «y = 6√x +
5√1 + x»
также есть корень пятой степени
«5√1 + x
».
Степень корня «5» — нечётное число, значит, никаких ограничений на подкоренное выражение
«1 + x»
не накладывается.
Получается, что единственное ограничение области определения функции
«y = 6√x +
5√1 + x»
— это ограничение подкоренного выражения
«6√x».
x ≥ 0
Нарисуем область определения функции на числовой оси и запишем ответ.
Ответ:
D(y): x ∈ [0 ; +∞)
Разбор примера
Найдите область определения функции:
Есть ли в функции знаменатель, в котором содержится « x »? В заданной функции подобных знаменателей два.
Выделим знаменатели с « x » красным цветом.
Запишем условие, что каждый из знаменателей не должен быть равен нулю.
| √x + 2 ≠ 0 | |
| x2 − 7x + 6 ≠ 0 |
Обозначим их номерами «1» и
«2» и решим каждое уравнение отдельно.
| √x + 2 ≠ 0 (1) | |
| x2 − 7x + 6 ≠ 0 (2) |
Решаем первое уравнение.
√x + 2 ≠ 0 (1)
Если значение квадратного корня
«√x + 2 ≠ 0» не должно быть равно нулю,
значит, подкоренное выражение
«x + 2 ≠ 0»
также не должно быть равно нулю.
√x + 2 ≠ 0 (1)
x + 2 ≠ 0
x ≠ −2
Теперь решим уравнение под номером «2», используя
формулу квадратного уравнения.
x1;2 =
x2 − 7x + 6 ≠ 0 (2)
x1;2 =
| −(−7) ± √(−7)2 − 4 · 1 · 6 |
| 2 · 1 |
x1;2 =
x1;2 =
x1;2 =
Запишем все полученные ответы в порядке возрастания вместе под знаком системы, чтобы их не забыть.
Знаменатели с « x »
мы проверили. Настала очередь
проверить
формулу функции
на
наличие корней четной степени .
В формуле функции
«f(x) =
+
»
есть два корня
«√x − 4» и
«√x + 2». Их подкоренные
выражения должны быть больше или равны нулю.
Решим полученную
систему неравенств.
Нарисуем полученные решения на числовой оси. Выберем заштрихованный промежуток, который есть на обеих числовых осях.
Выпишем результат решения системы неравенств.
x ≥ 4
Объединим в таблицу ниже полученные ответы по обеим
проверкам:
- проверка, что знаменатели
дробей
с « x »
не равны нулю; - проверка, что
подкоренные выражения корней четной степени должно быть больше или равны нулю.
| Условие проверки | Результат |
|
Результат проверки, что знаменатели дробей с « x » не равны нулю |
|
|
Результат проверки, что подкоренные выражения должно быть больше или равны нулю |
x ≥ 4 |
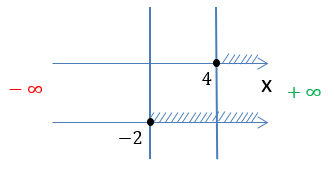
Нарисуем полученные результаты проверок на числовых осях, чтобы определить, какая заштрихованная область удовлетворяет
всем полученным условиям.
Запишем окончательный ответ для области определения функции
«f(x) =
+
»
с использованием математических символов.
Ответ:
D(y): x ∈ [4 ; 6) ∪ (6; +∞)
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
17 декабря 2016 в 18:02
Татьяна Цыганова
Профиль
Благодарили: 0
Сообщений: 1
Татьяна Цыганова
Профиль
Благодарили: 0
Сообщений: 1
Найти ОДЗ функции у=?(р1+р2х+x2)
Я не могу понять за какое число воспринимать p1, p2
0
Спасибо
Ответить
17 декабря 2016 в 19:10
Ответ для Татьяна Цыганова
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
x2 + p2x + p1 ? 0.
0
Спасибо
Ответить
24 февраля 2016 в 20:29
Влад Алексеев
Профиль
Благодарили: 0
Сообщений: 1
Влад Алексеев
Профиль
Благодарили: 0
Сообщений: 1
Постройте график функции y=-
. Укажите область определения функции
0
Спасибо
Ответить
25 февраля 2016 в 8:10
Ответ для Влад Алексеев
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Область определения функции: знаменатель не равен 0.
x+1?0
x?-1
Графиком является гипербола, смещеная влево относительно оси Y.
0
Спасибо
Ответить
5 февраля 2018 в 14:30
Ответ для Влад Алексеев
Кирилл Косован
Профиль
Благодарили: 0
Сообщений: 1
Кирилл Косован
Профиль
Благодарили: 0
Сообщений: 1
0
Спасибо
Ответить
11 февраля 2018 в 15:44
Ответ для Влад Алексеев
Татьяна Мирная
Профиль
Благодарили: 0
Сообщений: 1
Татьяна Мирная
Профиль
Благодарили: 0
Сообщений: 1
у=-
0
Спасибо
Ответить
7 октября 2015 в 21:21
Катерина Яроцкая
Профиль
Благодарили: 0
Сообщений: 1
Катерина Яроцкая
Профиль
Благодарили: 0
Сообщений: 1
Помогите найти область определения функции
0
Спасибо
Ответить
12 сентября 2016 в 15:59
Ответ для Катерина Яроцкая
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
К сожалению, картинка не отражается.
0
Спасибо
Ответить

Онлайн калькуляторы
На нашем сайте собрано более 100 бесплатных онлайн калькуляторов по математике, геометрии и физике.

Справочник
Основные формулы, таблицы и теоремы для учащихся. Все что нужно, чтобы сделать домашнее задание!

Заказать решение
Не можете решить контрольную?!
Мы поможем! Более 20 000 авторов выполнят вашу работу от 100 руб!
Область определения функции
Нахождение области определения функции
Схема нахождения области определения функций:
- Если
представляет собой многочлен, то областью определения функции
будет множество всех действительных чисел.
- Если
— рациональная дробь, то областью является множество всех действительных чисел кроме тех значений
, при которых знаменатель равен нулю.
- Если функция имеет вид
, то областью определения будет множество решений неравенства
.
- Если функция имеет вид
, где
некоторый многочлен, то областью определения будет множество решений неравенства
.
- Область определения суммы, разности или произведения двух или нескольких функций есть пересечение областей определений этих функций, для её отыскания составляется и затем решается система соответствующих условий.
- Для логарифмической функции
(
) областью определения есть интервал
.
Примеры решения задач
ПРИМЕР 1
| Задание | Найти область определения следующих функций:
|
| Решение | 1) Функцию Функция Функция Таким образом, область определения функции 2) Для нахождения области определения Разложим на множители левую часть этого неравенства. Для этого решим уравнение Обозначим найденные корни на числовой оси и определим знак неравенства на полученных интервалах.
Таким образом, 3) Функция Таким образом, |
| Ответ |
|
ПРИМЕР 2
| Задание | Найти область определения следующих функций:
|
| Решение | 1) Для нахождения области определения функции Поскольку основание степени Таким образом, 2) Для нахождения области определения функции Решим первое неравенство отдельно Согласно определению логарифма, придем к неравенству Возвращаясь к системе неравенств, имеем Таким образом, искомая область определения 3) Учитывая определение логарифмической функции, область определения В результате имеем, что |
| Ответ |
|
| Понравился сайт? Расскажи друзьям! | |
Нужна помощь с
решением задач?
Более 500 авторов онлайн и готовы помочь тебе прямо сейчас! Цена от 20 рублей за задачу. Сейчас у нас проходит акция, мы дарим 100 руб
на первый заказ.
Область определения функции
Сегодня потренируемся в отыскании области определения выражения и функции.
Когда отыскивают область определения функции, то часто она совпадает с областью определения выражения, задающего функцию: такая область определения называется естественной. Но бывает и так, что условия задачи накладывают особые ограничения: например, естественная область определения функции от (-8) до 8, но аргумент этой функции — время (или вес). Понятно тогда, что время (как и вес) не может быть отрицательной величиной и тогда естественная область определения такой функции сужается до промежутка (0; 8).
При отыскании области определения функции надо помнить о следующих ограничениях:
1. При извлечении корня четной степени подкоренное выражение обязано быть неотрицательным (что не запрещает ему быть равным нулю). 2. Знаменатель дроби не может быть равным нулю. 3. Выражение, стоящее под знаком логарифма, не может быть отрицательным или равняться нулю. 4. Выражение, стоящее под знаком арксинуса или арккосинуса, не может превышать 1 по модулю
Также надо помнить, что область определения всегда нужно искать для исходной функции, до каких-либо преобразований.
Например, функции 





1. Найдите область определения выражения:
Перепишем выражение:
Так как выражение стоит под корнем четной степени, значение его не должно быть отрицательным:

Дробь положительна, если числитель и знаменатель ее одновременно положительны или отрицательны. У нас в числителе положительное число, поэтому знаменатель неотрицателен. Кроме того, знаменатель не может быть равен нулю, поэтому неравенство становится таким:

Получили квадратное неравенство. Находим корни квадратного уравнения, чтобы выяснить точки перемены знака:
Наносим полученные точки на координатную прямую и расставляем знаки. Так как 
Ответ: 
2. Найдите область определения выражения:
Так как выражение стоит под корнем четной степени, значение его не должно быть отрицательным:

Получили квадратное неравенство. Находим корни квадратного уравнения, чтобы выяснить точки перемены знака:
Наносим полученные точки на координатную прямую и расставляем знаки. Так как 
Ответ: ![{x}in=[{{5-sqrt{41}}/4};{{5+sqrt{41}}/4}] {x}in=[{{5-sqrt{41}}/4};{{5+sqrt{41}}/4}]](https://easy-physic.ru/img_formuls/math_986_d5283fd254f051616bcd6dad000a9347.png)
3. Найдите область определения функции:
Очевидно, что область определения функции будет совпадать с областью определения выражения 


Изображаем полученные точки на числовой оси, ставим знаки:
Точки закрашены, концы интервалов входят в решение. Тогда область определения функции: 



4. Найдите область определения функции:
Очевидно, что область определения функции будет совпадать с областью определения выражения 



Изображаем полученные точки на числовой оси:
Решение системы неравенств:
Область определения функции: 

5. Найдите область определения функции:
Очевидно, что область определения функции будет совпадать с областью определения выражения
– ищем естественную область определения функции. Данное выражение имеет смысл только при 

Рассмотрим два случая:
Решение:
Или
Решение:
Область определения функции: 

6. Найти область определения функции:
Решение:
Ответ:
7. Найти область определения функции:
Решение:
Ответ:
8. Найти область определения функции:
Решение:
Ответ:

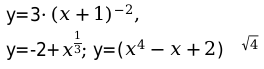
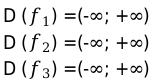
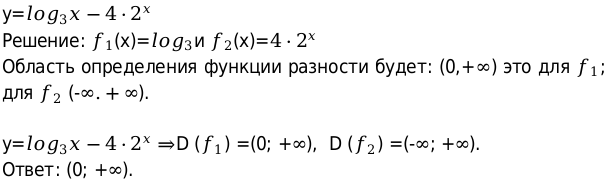

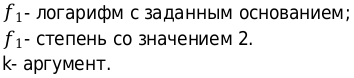
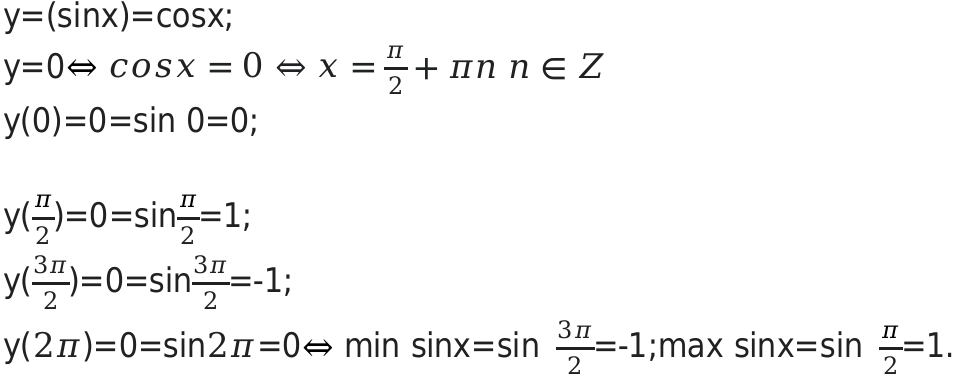
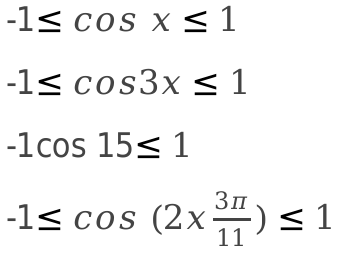
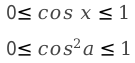
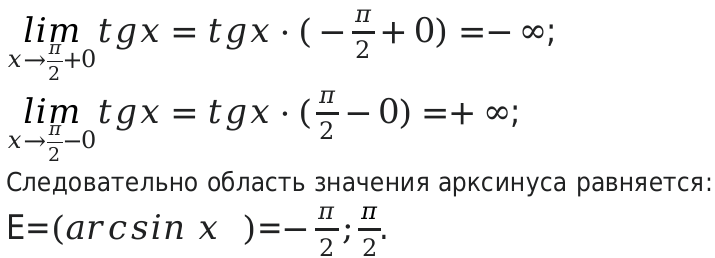

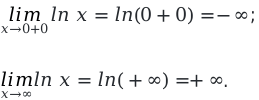
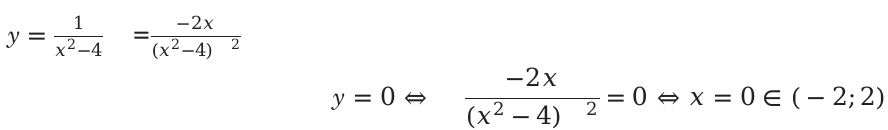
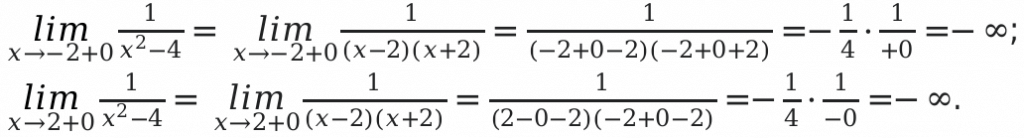
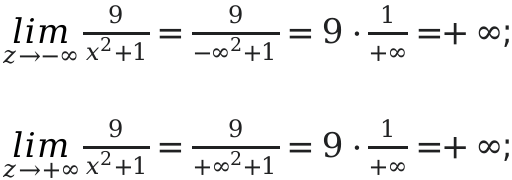
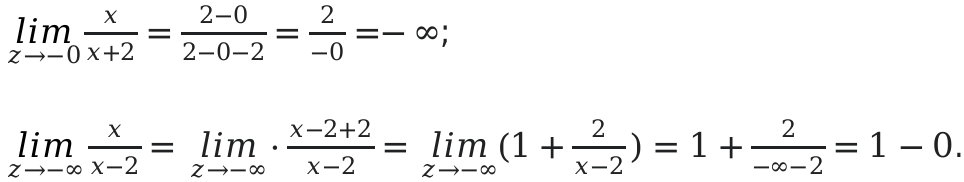
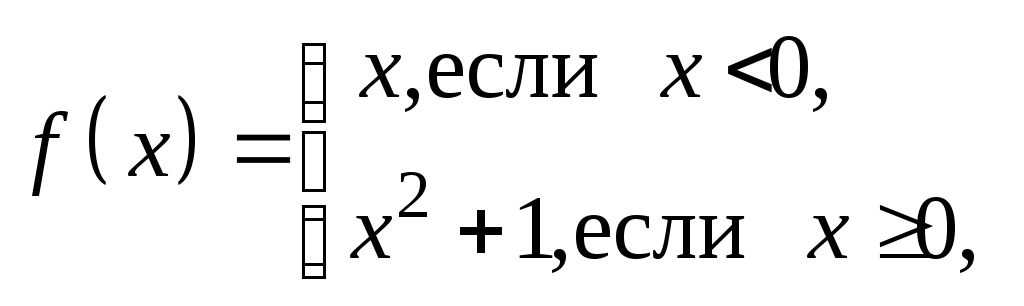

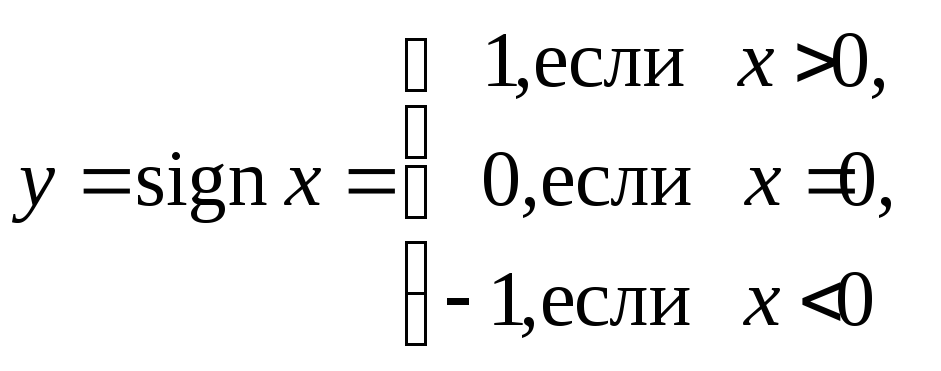


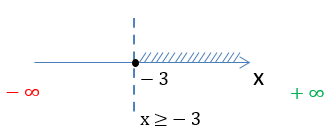
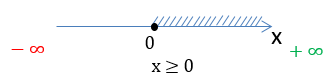











![Rendered by QuickLaTeX.com [left{begin{array}{l} {x>0,} \ {xne 1,} \ {x-0,5>0,} end{array}right. quad Rightarrow quad left{begin{array}{l} {x>0,} \ {xne 1,} \ {x>0,5;} end{array}right. quad Rightarrow quad left{begin{array}{l} {xne 1,} \ {x>0,5;} end{array}right. Rightarrow left(0,5;; 1right)bigcup left(1;+infty right)]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-280d0745fdd860d7a5c3c1e8c2a7d34c_l3.png)
















































