Преподаватель который помогает студентам и школьникам в учёбе.
Содержание:
Определение функции y=tg x
Определение:
Зависимость, при которой каждому действительному числу
Пример:
Определите, принадлежит ли графику функции 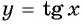
Решение:
а) Подставим в формулу 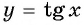
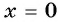
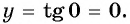
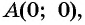
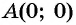
б) При 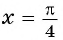
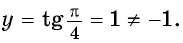
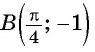
в) При 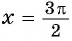
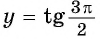
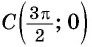
Определение функции y=ctg x
Определение:
Зависимость, при которой каждому действительному числу 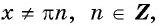
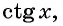
Пример:
Верно ли, что график функции 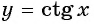
Решение:
а) Подставим в формулу 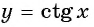
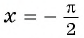
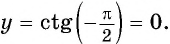
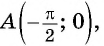
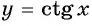
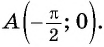
б) При 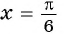
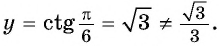
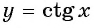
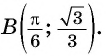
в) При 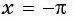
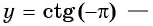
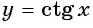
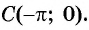
Свойства функций y=tg x и y=ctg x
Рассмотрим свойства этих функций:
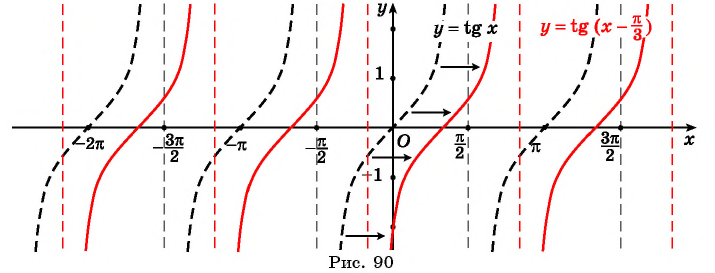
График функции y=tg x
График функции 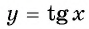
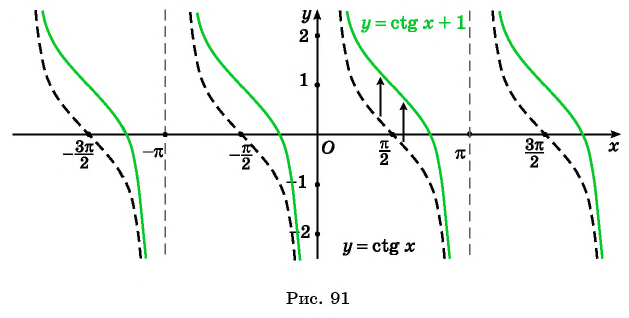
График функции y=ctg x
График функции 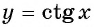
Примеры заданий и их решения
Пример №1
Найдите область определения функции:
Решение:
а) Так как область определения функции 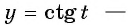
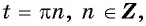
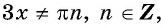
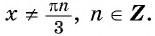
б) Областью определения функции 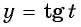
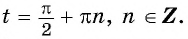
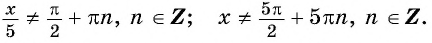
Пример №2
Найдите множество значений функции:
Решение:
а) Так как множество значений функции 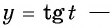
б) Так как множество значений функции 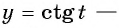
Пример №3
Используя свойство периодичности функций 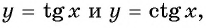
Решение:
Так как число 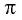
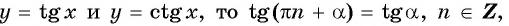
- Заказать решение задач по высшей математике
Пример №4
Используя свойство нечетности функций 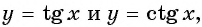
Решение:
Так как функции 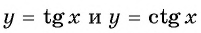
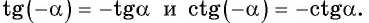
Пример №5
Определите знак произведения
Решение:
Так как 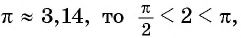
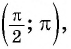
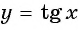
Угол 4,5 радиана принадлежит промежутку 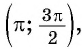
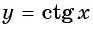
Угол 7 радиан принадлежит промежутку 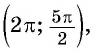
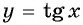
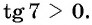
Пример №6
Что больше:
Решение:
Поскольку углы 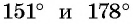
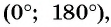
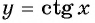
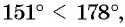
Пример №7
Постройте график функции:
Решение:
а) График функции 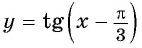
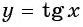
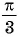
б) График функции 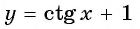
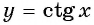
- Арксинус, арккосинус, арктангенс и арккотангенс числа
- Тригонометрические уравнения
- Тригонометрические неравенства
- Формулы приведения
- Определение тангенса и котангенса произвольного угла
- Соотношения между синусом, косинусом, тангенсом и котангенсом одного и того же угла (тригонометрические тождества)
- Функция y=sin x и её свойства и график
- Функция y=cos x и её свойства и график
Объяснение и обоснование
Напомним, что . Таким образом, областью определения функции y=будут все значения аргумента, при которых , то есть все значения x, kZ. Получаем
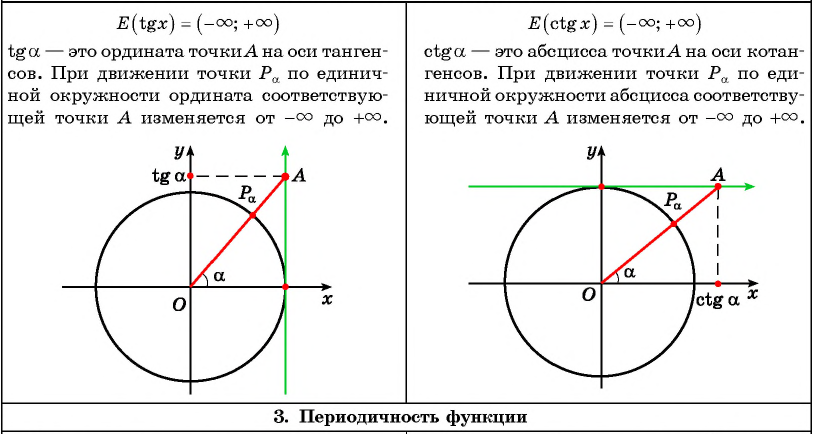
Этот результат можно получить и геометрически. Значения тангенса – это ордината соответствующей точки на линии тангенсов (рис.91). Поскольку точки Aи B единичной окружности лежат на прямых ОА и ОВ, параллельных линии тангенсов, мы не сможем найти значение тангенса дляx, kZ.
Для всех других значений аргумента мы можем найти соответствующую точку на линии тангенсов и ее ординату — тангенс. Следовательно, все
Значенияx входят в область определения функции y=tgx.
Для точек единичной окружности (которые не совпадают с точками А и В) ординаты соответствующих т
очек на линии тангенсов принимают
все значения до +, поскольку для любого действительного числа
мы можем указать соответствующую точку на оси ординат, а значит, и соответствующую точку на оси тангенсов. Учитывая, что точка О лежит
внутри окружности, а точка вне ее (или на самой окружности), получаем, что прямая имеет с окружностью хотя бы одну общую точку
(на самом деле их две). Следовательно, для любого действительного числа
найдется аргумент х, такой, что tan x равен данному действительному числу.
Поэтому область значений функции y= tg x — все действительные числа,
то есть R. Это можно записать так: E (=tgx) = R. Отсюда следует, что наибольшего и наименьшего значений функция tan x не имеет.
Как было показано в § 13, тангенс — нечетная функция:tg(-x)=tg x, следовательно, ее график симметричен относительно начала координат.
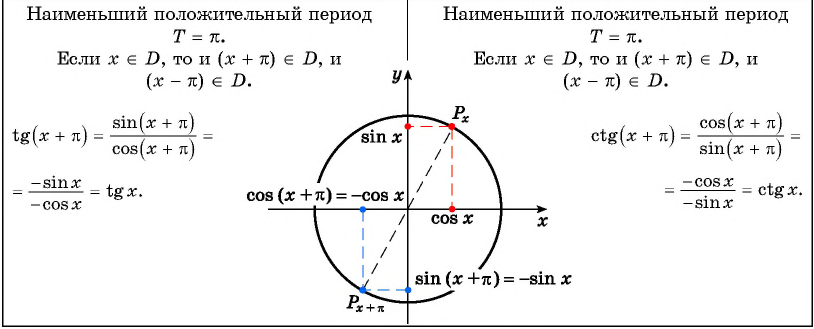
Тангенс — периодическая функция с наименьшим положительным периодом
Поэтому при построении графика
этой функции достаточно построить график на любом промежутке длиной π,
а потом полученную линию перенести параллельно вправо и влево вдоль оси
Ox на расстоянияkT = πk, где k — любое натуральное число.
Чтобы найти точки пересечения графика функции с осями координат,
напомним, что на оси Oy значение x = 0. Тогда соответствующее значение
y = tg 0 = 0, то есть график функции y = tg x проходит через начало координат.
На оси Ox значение y = 0. Поэтому необходимо найти такие значения x,
при которых tg x, то есть ордината соответствующей точки линии тангенсов, равна нулю. Это будет тогда и только тогда, когда на единичной окружности будут выбраны точки C или D, то есть при x = πk, k ∈ Z.
Промежутки знакопостоянства. Как было обосновано в § 13, значения
функции тангенс положительны (то есть ордината соответствующей точкилинии тангенсов положительна) в І и ІІІ четвертях. Следовательно, tgx > 0 при
а также, учитывая период, при всех
Значения функции тангенс отрицательны (то есть ордината соответствующей точки линии тангенсов отрицательна) во ІІ и ІV четвертях. Такимобразом,
Промежутки возрастания и убывания.
Учитывая периодичность функции tgx (период T = π), достаточно исследовать ее на возрастание и убывание на любом промежутке длиной π,
например на промежутке . Если x (рис. 92), то при увеличении аргумента x (x2>x1) ордината соответствующей точки линии
тангенсов увеличивается (то есть tgx2>tgx1). Таким образом, на этом
промежутке функция tgx возрастает. Учитывая периодичность функции
tgx, делаем вывод, что она возрастает также на каждом из промежутков
Проведенное исследование позволяет обоснованно построить график
функции y = tg x. Учитывая периодичность этой функции (с периодом π),
сначала построим график на любом промежутке длиной π, например на промежутке . Для более точного построения точек графика воспользуемся также тем, что значение тангенса — это ордината соответствующей точки
линии тангенсов. На рисунке 93 показано построение графика функции
y = tg x на промежутке.
Далее, учитывая периодичность тангенса (с периодом π), повторяем вид
графика на каждом промежутке длиной π (то есть параллельно переносим
график вдоль оси Ох на πk, где k — целое число).
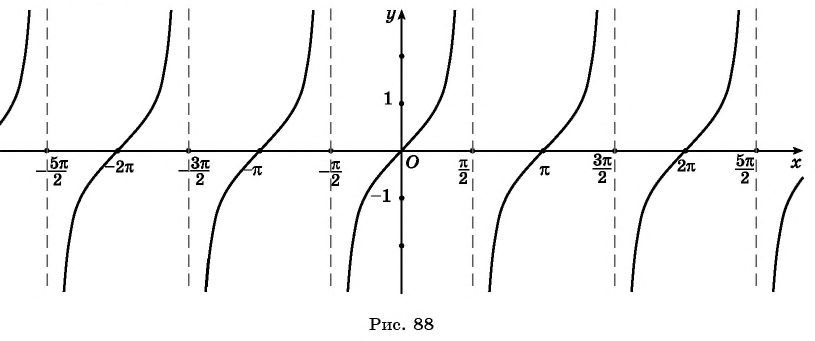
Получаем график, приведенный на рисунке 94, который называется тангенсоидой.
14.4. СВОЙСТВА ФУНКЦИИ y = ctg x И ЕЕ ГРАФИК
Объяснение и обоснование
Так как =, то областью определения котангенса будут все значения аргумента, при которых sin х ≠ 0, то есть x ≠ πk, k ∈ Z. Такимобразом,
D (ctg x): x ≠ πk, k ∈ Z.
Тот же результат можно получить, используя геометрическую иллюстрацию. Значение котангенса — это абсцисса соответствующей точки на линии
котангенсов (рис. 95).
Поскольку точки А и В единичной окружности лежат на прямых ОА
и ОВ, параллельных линии котангенсов, мы не можем найти значение котангенса для x = πk, k ∈ Z. Длядругихзначенийаргументамыможемнайтисоответствующуюточкуна линии котангенсов и ее абсциссу — котангенс. Поэтому все значения x ≠ πk входят в область определения функции у = ctg х.
Для точек единичной окружности (которые не совпадают с точками А и В) абсциссы соответствующих точек на линии котангенсов принимают все значения от –× до +×, поскольку для любого действительного числа мы можем указать соответствующую точку на оси абсцисс, а значит, и соответствующую точку Qх на оси котангенсов. Учитывая, что точка О лежит внутри окружности, а точка Qх — вне ее (или на самой окружности), получаем, что прямая ОQх имеет с окружностью хотя бы одну общую точку (на самом деле их две). Следовательно, для любого действительного числа найдется аргумент х, такой, что сtg x равен данному действительному числу. Таким образом, область значений функции y = ctg x — все действительные числа, то есть R.
Это можно записать так: E (ctgx) = R.Из приведенных рассуждений также вытекает, что наибольшего и наименьшего значений функция ctgxне имеет.
Как было показано в § 13, котангенс — нечетная функция: ctg (-x) = -ctgx, поэтому ее график симметричен относительно начала координат.
Там же было обосновано, что котангенс — периодическая функция с наименьшим положительным периодом T= : ctg (x+ ) = ctg x, поэтому через промежутки длиной п вид графика функции ctgxповторяется.
Чтобы найти точки пересечения графика функции с осями координат, напомним, что на оси Oyзначение x= 0. Но ctg0 не существует, значит, график функции y= ctg x не пересекает ось Oy.
На оси Оx значение y= 0. Поэтому необходимо найти такие значения x, при которых ctgx, то есть абсцисса соответствующей точки линии котангенсов, равна нулю. Это будет тогда и только тогда, когда на единичной окружности будут выбраны точки C или D(рис. 95), то есть при
Промежутки знакопостоянства. Как было обосновано в § 13, значения функции котангенс положительны (то есть абсцисса соответствующей точки линии котангенсов положительна) в I и III четвертях (рис. 96). Тогда ctgx> 0 при всех . Учитывая период, получаем, что ctgx> 0 при всех
Значения функции котангенс отрицательны (то есть абсцисса соответствующей точки линии котангенсов отрицательна) во II и IV четвертях, таким образом, ctgx< 0 при .

Промежутки возрастания и убывания
Учитывая периодичность функции ctg x (наименьший положительный период T = ), достаточно исследовать ее на возрастание и убывание на любом промежутке длиной , например на промежутке (0; ). Если (0; ) (рис. 97), то при увеличении аргумента x (x2>x1) абсцисса соответствующей точки линии котангенсов уменьшается (то есть ctgx2<ctgx1), следовательно, на этом промежутке функция ctg x убывает. Учитывая периодичность функции y= ctgx, делаем вывод, что она также убывает на каждом из промежутков
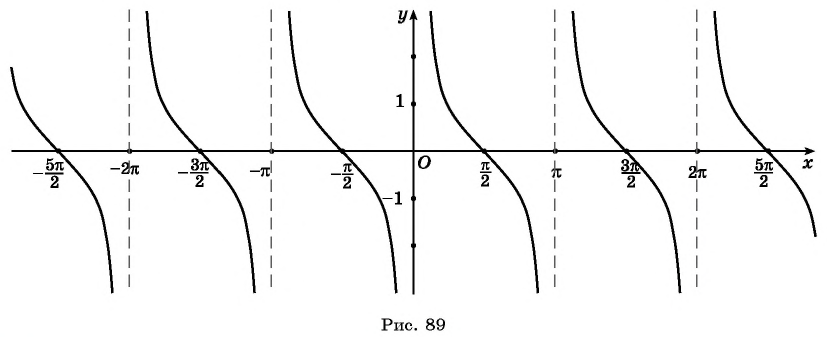
Проведенное исследование позволяет построить график функции y= ctg x аналогично тому, как был построен график функции y= tg x. Но график функции у = ctg x можно получить также с помощью геометрических преобразований графика функции у = tg х. По формуле, приведенной на с. 172, , то есть Поэтому график функции у = ctg x можно получить из графика функции у = tg х параллельным переносом вдоль оси Ох на (− ) и симметричным отображением полученного графика относительно оси Ох. Получаем график, который называется котангенсоидой (рис. 98).
Область определения и
множество значений
тригонометрических
функций
ОГЛАВЛЕНИЕ:
1.
Определение
«функция»;
2.
Какие функции
называются тригонометрическими;
3.
Что такое область
определения и множество значений функций. Как найти область определения и множество значений
тригонометрических функций;
4. Таблица «Область определения и множество
значений тригонометрических функций».
1. Функция — это зависимость одной переменной
величины от другой. То есть, это зависимость между величинами.
«x» называют
аргументом функции (переменной), «y» называют значением функции.
Рассмотрим
на простом примере (y=2x), как мы видим «y»
зависит от «х», так
как «х» переменный
аргумент, вместо него мы выбираем любые значения и подставляем в уравнение,
получая при этом значение «у».
2. Какие же
функции называются тригонометрическими?
Тригонометрические функции — это элементарные функции, с переменным аргументом, в которых служит угол, то есть «х»
является определённым углом.
Зачастую
тригонометрические функции обозначают отношением сторон прямоугольного
треугольника либо длины конкретных отрезков в единичной окружности. Такие
функции имеют вид:
1. y=sinx
2. y=cosx
3. y=tgx
4.
y=ctgx
3. Начнем с
области определения.
Областью
определения функции называется множество значений аргумента «х», на
котором можно задать эту функцию «у».
Множеством значения функций называют множество, состоящее их всех
значений, которые принимает функция.
Рассмотрим
функции y=tgx, у=ctg, sinx, cosx на единичной окружности.
Функция
y=tgx определяется из ΔOAB как tgx=AB/OB=sinx/cosx.
Эта
функция определена при тех значениях, для которых cosx≠0.
Следовательно,
областью определения функции y=tgx является всё множество действительных чисел,
исключая x=π/2+πn, n∈Z.
Множеством
значений функции y=tgx является множество всех действительных чисел R.
Функция y=ctg определяется из ΔOAB как ctgx=OB/AB=cosx/sinx.
Эта функция
определена при тех значениях, для которых sinx≠0.
Следовательно,
областью определения функции y=ctgx является всё множество действительных
чисел, исключая x=πn, n∈Z.
Множеством
значений функции y=ctgx является множество всех действительных чисел R.
AB=sinx;OB=cosx .
Тем
самым каждому действительному числу x поставлены в соответствие числа sinx и
cosx, то есть на множестве R всех действительных чисел определены функции
y=sinx и y=cosx.
Таким
образом, областью определения функций y=sinx и y=cosx является множество R всех
действительных чисел.
Множеством
значений функций y=sinx и y=cosx является интервал [−1;1].
4. Таблица:
«Область определения и множество значений тригонометрических функций»
Источники:
1.
https://videouroki.net/video/01-oblast-opredeleniya-i-mnozhestvo-znachenij-trigonometricheskih-funkcij.html
2.
https://www.yaklass.ru/p/algebra/10-klass/trigonometricheskie-funktcii-10781/trigonometricheskie-funktcii-chislovogo-argumenta-10782/re-90ce54f0-d7df-47e5-becb-006ab01487e9
Число, равное отношению синуса угла α (α ≠ π/2 + πk, kЄZ) к косинусу этого угла, есть тангенс угла α, его обозначают tgα. Поскольку для каждого значения величины х, кроме x = π/2 + πk, kЄZ, установлено взаимно-однозначное соответствие со значениями у = tgx , то тем самым задана функция у = tgx .
Свойства этой функции следуют из свойств функций y = sinx и y = cosх .
Поскольку функции у = sinх и y = cosх определены при всех значениях переменной х, область определения функции у = tgx это все действительные числа, за исключением тех точек, где cosх равен нулю, т. е. за исключением точек x = π/2 + πn, nЄZ.
Область значений функции у = tgx это всех действительные числа.
Функция у = tgx является периодической с основным периодом π: tg(α + πn) = tgα для любых αЄR, nЄZ.
Функция у = tgx нечетная, поскольку для любого значения х, которое принадлежит области определения является верным равенство tg(-x) = -tgx.
График функции у = tgx пересекается с осью Ох в точках с абсциссами, определяемыми уравнением tgx = 0, значит х = πn, nЄZ. График функции у = tgx пересекает ось Оу в единственной точке с ординатой y = 0.
Значения функции у = tgx положительны для углов, расположенных в I и III четвертях, и отрицательны для углов, расположенных во II и IV четвертях:
tgx > 0 при x Є (0 + πk; π/2 + πk), kЄZ;
tgх < 0 при x Є (-π/2 + πk; 0 + πk), kЄZ.
Функция у = tgx не имеет наибольшего и наименьшего значений.
Функция у = tgx не является монотонной. Она возрастает при x Є (-π/2 + πn; π/2 + πn), nЄZ.
Функция у = tgx непрерывна и имеет производную в каждой точке области из определения.
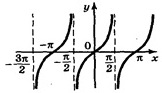
График рассматриваемой функции у = tgx показан на рисунке. График функции тангенс это набор линий, которые симметричны относительно начала координат и имеет вертикальные асимптоты x = π/2 + πn, nЄZ.
План изучения темы
- Область определения и множество значений тригонометрических функций.
- Чётность, нечётность, периодичность тригонометрических функций.
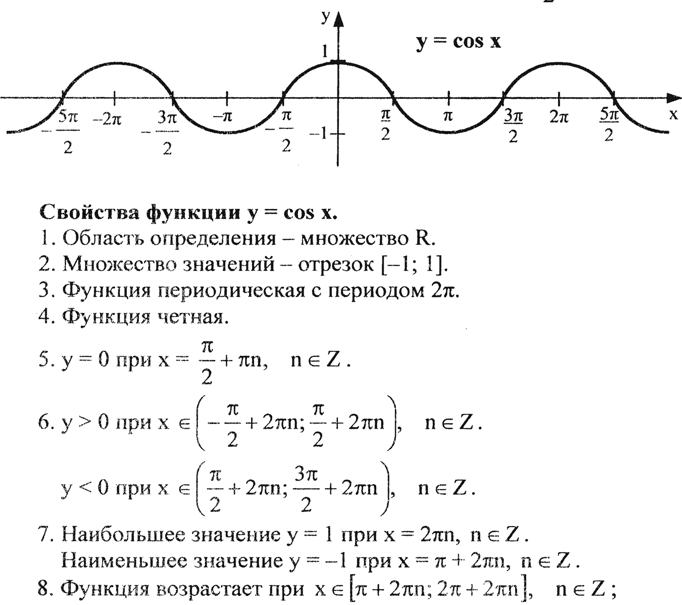
- Свойства функции y=cosx и её график.
- Свойства функции y=sinx и её график.
- Свойства функции y=tgx и её график.
- Свойства функции y=ctgx и её график.
- Решение задач на применение свойств функций.
Область определения и множество значений тригонометрических функций
Область определения функции — это множество значений, принимаемых независимой переменной (аргументом Х). Для функции, заданной формулой, под область определения часто понимают множество допустимых значений аргумента, то есть всех тех его значений, для которых формула даёт действительное значение для функции.
Разберемся, какая область определения у тригонометрических функций. Каждому действительному числу Х соответствует единственная точка единичной окружности, получаемая поворотом точки (1;0) на угол Х радиан. Таким образом каждому действительному числу Х поставлены в соответствие числа sinx и cosx, т.е. на множестве R всех действительных чисел определены функции y=sinx и y=cosx.
Областью определения функций y=sinx и y=cosx является множество R всех действительных чисел.
Областью определения функции y=tgx является множество чисел
Множество значений функции — это множество значений, принимаемых зависимой переменной (Y).
Так как функции y=sinx и y=cosx принимают значения в рамках единичной окружности, то множество их значений ею ограничено.
Множеством значений функций y=sinx и y=cosx является отрезок [-1;1].
Функции y=sinx и y=cosx являются ограниченными.
Множеством значений функции y=tgx является множество R всех действительных чисел, так как уравнение tgx=a имеет корни при любом действительном значении a.
Пример 1
Найти область определения функции
Решение: сами функции y=sinx и y=cosx имеют в области определения все действительные числа. Но тут они стоят в сумме, в знаменателе. А мы знаем, что если знаменатель будет равным нулю, то выражение потеряет смысл. Значит, для нахождения области определения необходимо приравнять знаменатель к нулю и решить получившееся уравнение.
Значит, областью определения являются все значения, кроме найденных выше:
Пример 2
Найдите множество значений функции
Решение: видим, что в правой части есть возможность применить тригонометрическую формулу двойного угла для синуса. Сделаем это:
Областью значений функции y=sinx является отрезок [-1;1]. Здесь есть функция синуса, просто она умножена на одну вторую и ещё прибавлено 3. Учтём всё сказанное и получим новое множество значений:
То есть на первом шаге мы умножили концы отрезка на одну вторую, а затем прибавили к ним 3. В итоге мы получили множество значений данной функции. Никакой роли тут не играет двойной угол, так как он влияет на сужение/растяжение графика вдоль оси ОХ.
Ответ: [2,5;3,5]
Чётность, нечётность, периодичность тригонометрических функций
Чётная функция — функция y=f(x), область определения которой симметрична относительно нуля и для каждого Х из области определения имеет место равенство:
График чётной функции симметричен относительно оси ординат. Примером может служить парабола.
Нечетная функция — функция y=f(x), область определения которой симметрична относительно нуля и для каждого Х из области определения имеет место равенство:
График нечётной функции симметричен относительно начала координат. Примером может служить кубическая парабола.
значит, это нечётная функция.
значит, это чётная функция.
значит, это нечётная функция.
значит, это нечётная функция.
Пример 3
Выяснить, является ли функция чётной или нечётной:
Решение:
После применения формулы приведения, мы получаем функцию в виде
Воспользуемся правилом определения чётности/нечётности и проверим, что у нас получится:

Ответ: чётная
Период функции — некоторое действительное число Т такое, что для всех Х их области определения функции f числа Х+Т и Х-Т принадлежат области определения функции f и f(X)=f(X+T)=f(X-T). Однако чаще всего лишь наименьшее из всех таких чисел Т положительное, называют наименьшим периодом функции.
Мы с вами знаем, что при полном обороте по единичной окружности мы попадаем в точку с такими же координатами, то есть верны равенства:
Из этих равенств следует, что значения синуса и косинуса периодически повторяются при изменении аргумента на два пи. Такие функции называются периодическими с периодом:
Аналогично, выполняются ещё два равенства:
Значит, тангенс и котангенс — это периодические функции, с периодом:
Пример 4
Найдём несколько периодов функций на конкретных примерах.
Решение:
Задание 1. Смотрим, чем отличается функция от стандартного вида. Видим 3 перед аргументом. Значит, нужно взять основной период для синуса:
и просто поделить его на 3. Значит период для первой функции будет равен:
Задание 2. Перед аргументом у тангенса мы видим дробь 3/2. Значит, основной период тангенса нужно просто разделить на эту дробь. Получаем:
Задание 3. Перед аргументом стоит дробь 1/2 и прибавлено ещё пи на 6. Это прибавление не играет никакой роли, просто график будет двигаться налево вдоль оси, поэтому ищем период как обычно. Берём основной период косинуса и делим на дробь:
Задание 4. Видим у косинуса аргумент умножен на 4, значит просто на него делим основной период:
Задание 5. Перед аргументом у синуса дробь 1/5, просто делим на неё. Не обращаем на 4 впереди, это просто растяжение графика вдоль оси ОХ.
Задание 6. Перед аргументом синуса стоит 2, делим на неё:
Задание 7. У тангенса перед аргументом стоит 5. Берём основной период и делим на 5:
Задание 8. Аналогично тангенс, просто дробь впереди 1/2:
Задание 9. Тут уже нужно найти период для каждого слагаемого. Для синуса:
Для косинуса:
А общим периодом будет наименьшее общее кратное наших двух, которые мы нашли. То есть тот, который делится на каждый из найденных.


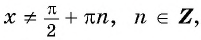
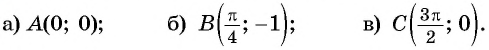
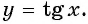
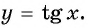
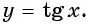
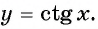
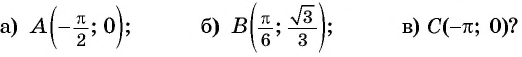



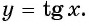


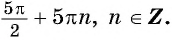

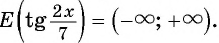
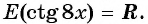
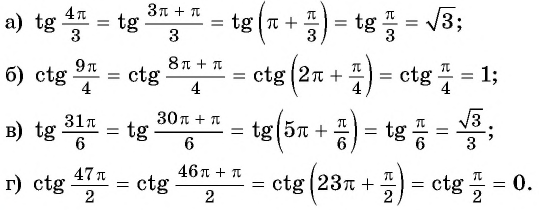


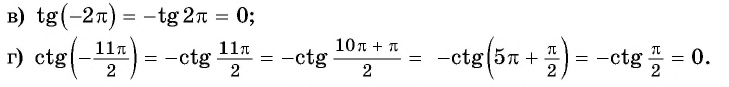
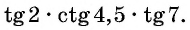
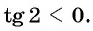
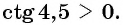
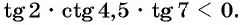
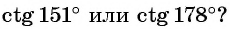
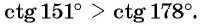





.png)









 Решение задач на применение свойств функций
Решение задач на применение свойств функций
