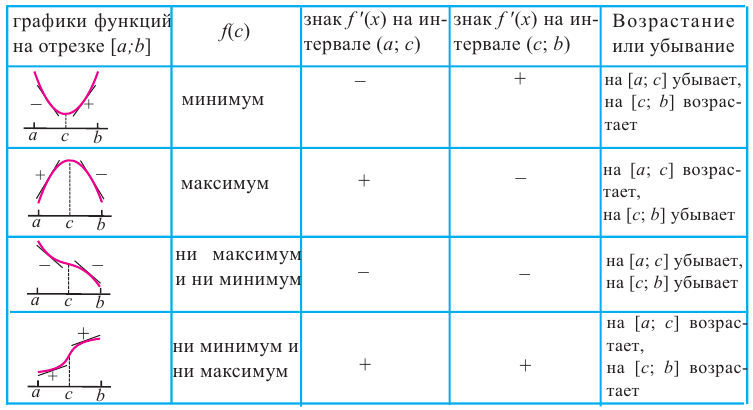
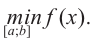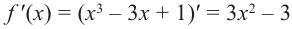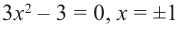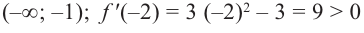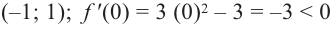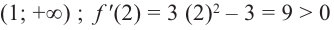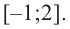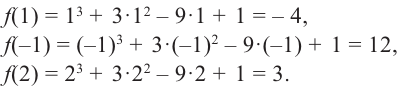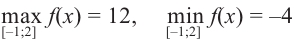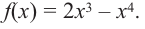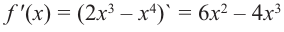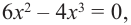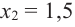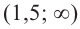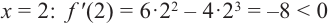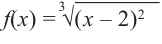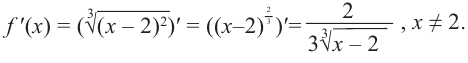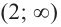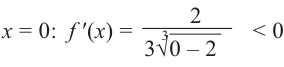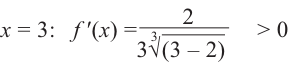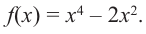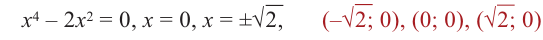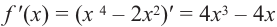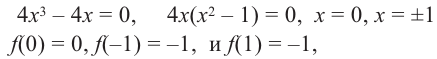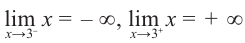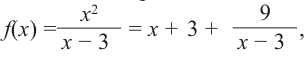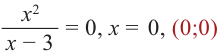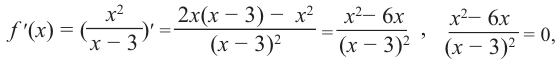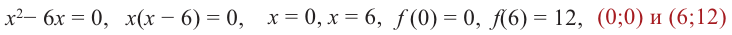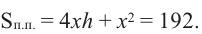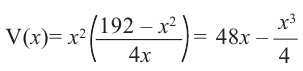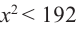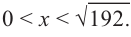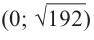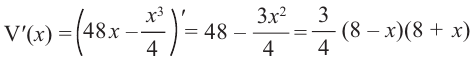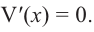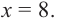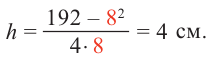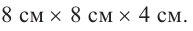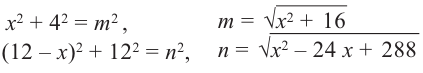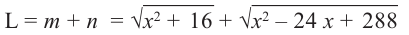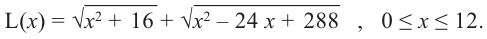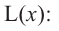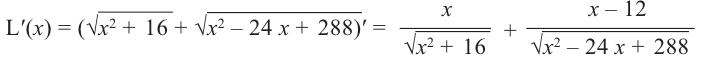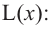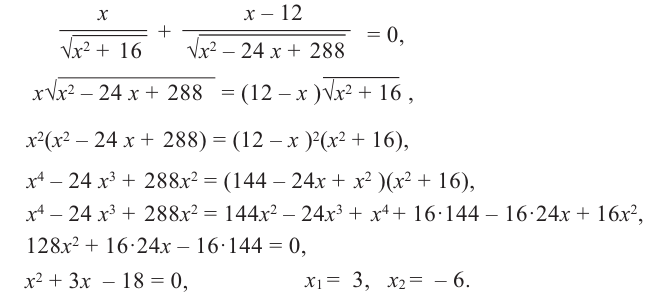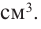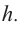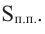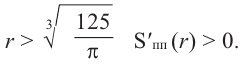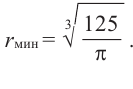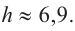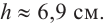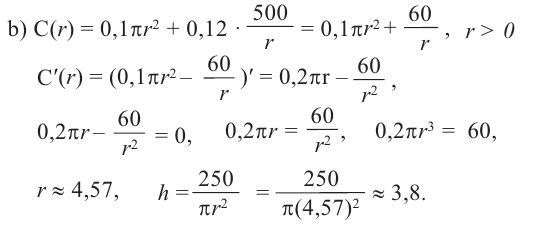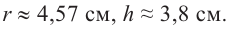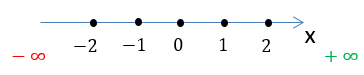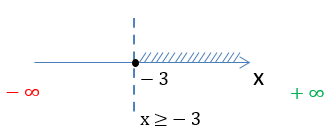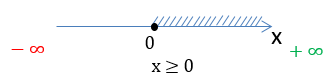Исследовать функцию — это значит установить её свойства: указать её область определения и область значений; промежутки возрастания и убывания; промежутки, на которых функция приобретает положительные значения, на которых — отрицательные; выяснить, не является ли данная функция чётной или нечётной и т. д.
Содержание:
Что такое исследование функции
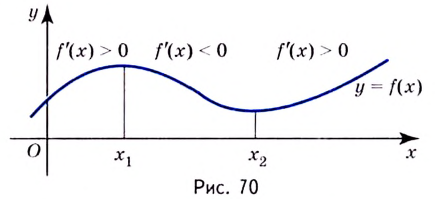
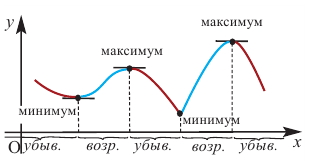
Одна из важных задач исследования функции — определение промежутков её возрастания и убывания. Как отмечалось, в тех точках, в которых функция возрастает, её производная (угловой коэффициент касательной) положительная, а в точках убывания функции её производная отрицательная {рис. 70).
Правильными будут следующие утверждения.
- Если производная функции в каждой точке некоторого промежутка положительная, то функция на этом промежутке возрастает.
- Если производная в каждой точке промежутка отрицательная, то функция на этом промежутке убывает.
- Если производная в каждой точке промежутка тождественно равна нулю, то на этом промежутке функция постоянная.
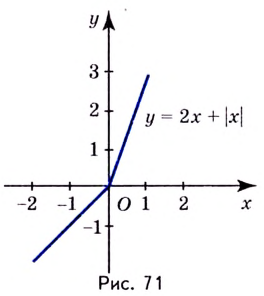
Строгое доказательство этого утверждения достаточно громоздкое, поэтому мы его не приводим. Заметим только, что в нём выражается достаточный признак возрастания или убывания функции, но не необходимый. Поэтому функция может возрастать и на промежутке, в некоторых точках которого она не имеет производной. Например, функция
Из сказанного следует, что два соседних промежутка, на одном из которых функция возрастает, а на другом — убывает, могут разделяться только такой точкой, в которой производная функции равна нулю или не существует.
Внутренние точки области определения функции, в которых её производная равна нулю или не существует, называют критическими точками функции.
Следовательно, чтобы определить промежутки возрастания и убывания функции 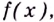
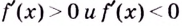
Пример:
Найдите промежутки возрастания и убывания функции
Решение:
Уравнение 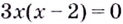
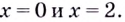
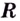
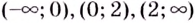
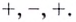
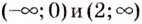
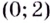
Замечание: Если функция непрерывна в каком-нибудь конце промежутка возрастания или убывания, то эту точку можно присоединить к рассматриваемому промежутку. Поскольку функция 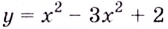
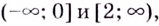
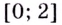
Пример:
Найдите промежутки убывания функции
Решение:
Критические точки: 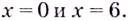
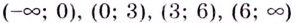
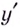
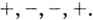
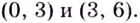
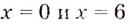
Пример:
Найдите критические точки функции 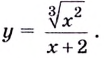
Решение:
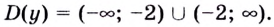
Найдём точки, в которых производная равна нулю или не существует: 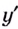
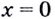
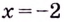

Ответ. 0 и 4.
Пример:
Докажите, что функция 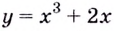
Решение:
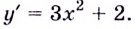
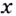
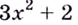
Пример:
Установите, на каком промежутке функция 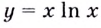
Решение:
Способ 1. 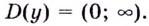
Найдём критические точки функции:
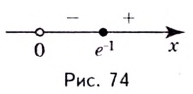
Эта точка разбивает область определения функции на два промежутка (рис. 74). Определим знак производной на каждом из них.
Следовательно, функция 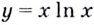
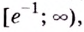
Способ 2. Решим неравенство 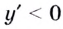
Ответ. Возрастает, если 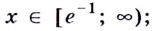
Применение второй производной к исследованию функций и построению их графиков
При помощи первой производной можно исследовать функцию на монотонность и экстремумы и схематично построить график. Оказывается, что поведение некоторых функций не всегда можно охарактеризовать, используя первую производную. Более детальное исследование проводится при помощи второй производной. Вспомним, что такое вторая производная.
Пусть функция 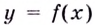
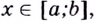
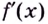
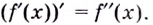
Например, найти производную 2-го порядка функции 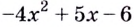
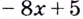
Кривая 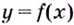
Кривая 
Точкой перегиба называется такая точка кривой, которая отделяет её выпуклую часть от вогнутой.
Интервалы выпуклости и вогнутости находят при помощи такой теоремы.
Теорема. Если вторая производная дважды дифференцируемой функции 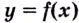
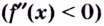
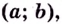
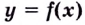
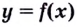
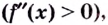
Из теоремы следует, что точками перегиба кривой 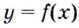
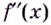
Установим до статочное условие существования точки перегиба.
Теорема. Пусть 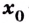
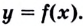
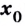
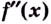
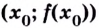
Для нахождения промежутков выпуклости и точек перегиба графика функции целесообразно пользоваться следующей схемой:
- найти область определения функции;
- найти критические точки второго рода;
- определить знак второй производной на образованных интервалах. Если
то кривая выпуклая; если
— кривая вогнутая;
- если производная
меняет знак при переходе через точку
то точка
является точкой перегиба кривой
Пример №1
Найдите интервалы выпуклости, вогнутости и точки перегиба кривой
Решение:
1) Область определения функции:
2) Найдём вторую производную: 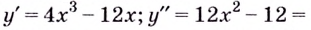
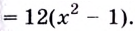
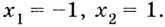
3) Разбиваем область определения на интервалы 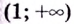
Если 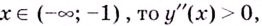
Если 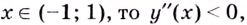
Если 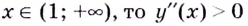
Следовательно, точки 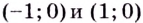
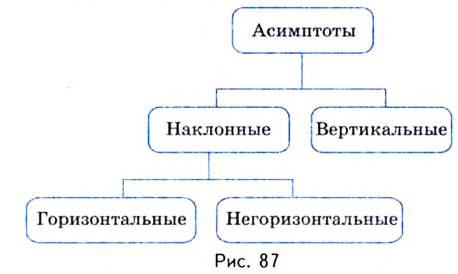
Напомним, что прямая 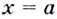
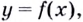
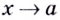
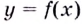
Уравнение наклонной асимптоты:
Если записанные пределы существуют, то существует наклонная асимптота; если хотя бы один из них не существует или равен 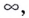
Если 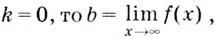
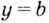
Замечание: Рассмотренные пределы могут быть односторонними, а под символом 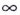
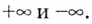
Пример №2
Найдите асимптоты кривых:
Решение:
а) 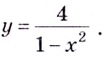
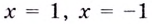
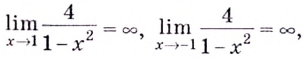
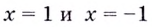
Найдём наклонную асимптоту: 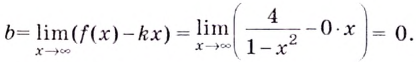
Следовательно, заданная кривая имеет три асимптоты:
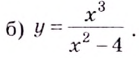
Поскольку функция не определена в точках 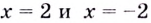
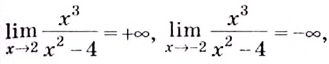
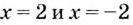
Для наклонной асимптоты
Значит прямая 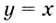
Итак, асимптоты кривой:
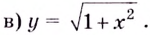
Следовательно, 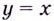
2) если 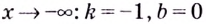

Следовательно, заданная кривая имеет две асимптоты:
Определение точек перегиба, интервалов выпуклости и асимптот существенно помогает в построении графиков различных функций.
Нахождение промежутков возрастания и убывания функции
Интервалы возрастания и убывания функции
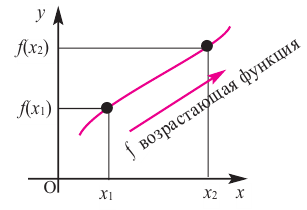
возрастающая функция
Если для любых 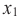
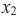
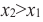
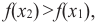
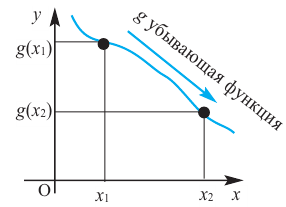
убывающая
Если для любых 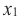
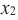
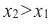
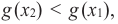
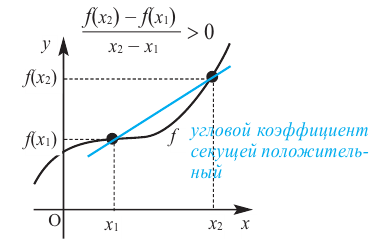
Связь промежутков возрастания и убывания функции с угловым коэффициентом секущей можно выразить следующим образом.
Если на заданном промежутке угловой коэффициент любой секущей положителен, то на этом промежутке функция 
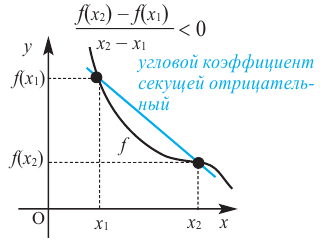
Если на заданном промежутке угловой коэффициент любой секущей отрицателен, то на этом промежутке функция 
Промежутки возрастания и убывания функции
Пусть на определенном промежутке производная функции 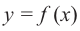
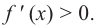
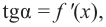
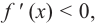
Теорема. Если функция 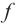
Примечание: если функция 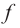
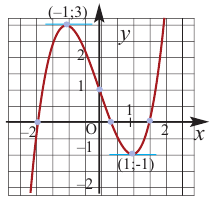
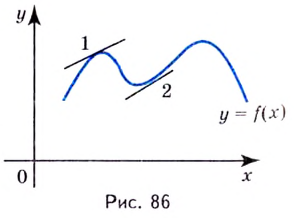
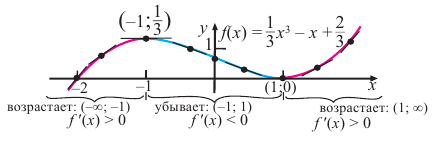
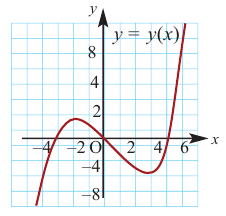
По графику функции 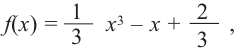
На интервалах 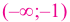
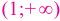
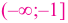
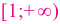
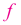
На интервале 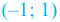
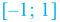
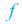
Пример №3
При помощи производной определите промежутки возрастания и убывания функции
Решение: 1. Алгебраический метод.
Найдем производную функции
Функция 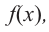
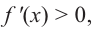
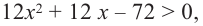
Для решения неравенства сначала надо решить соответствующее уравнение
Значит, при 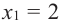
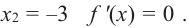
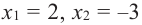
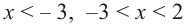
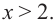
Из таблицы и непрерывности функции 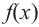
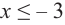
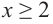
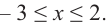
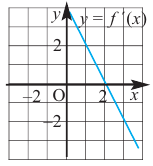
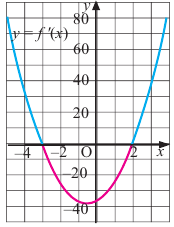
2. Промежутки возрастания и убывания функции можно определить но графику производной. На рисунке изображен график производной
График производной 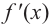
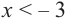
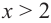
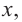
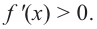
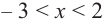
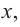
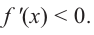
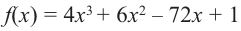
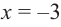
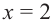
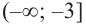
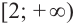
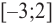
Пример №4
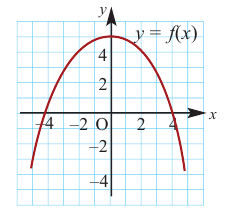
Изобразите схематично график непрерывной функции согласно еле дующим условиям:
a) при 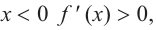
b) при 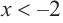
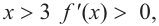
Решение:
а) при 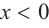
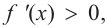
функция возрастает. При 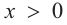
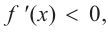
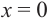
b) При 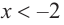
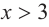
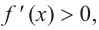
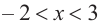
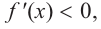
Критические точки и экстремумы функции
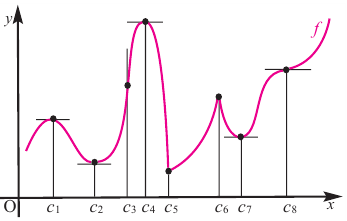
В некоторых точках из области определения производная функции может быть равна нулю или вообще может не существовать. Такие точки из области определения называются критическими точками функции. Покажем критические точки на графике заданной функции.
1. Для значений 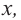
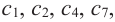
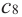
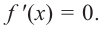
2. В точках 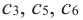
3. Для рассматриваемой нами функции критические точки 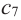
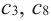
По графику видно, что в точках внутреннего экстремума(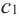
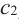
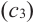
Теорема Ферма (Необходимое условие существовании экстремумов)
Во внутренних точках экстремума производная либо равна нулю, либо не существует.
Примечание. Точка, в которой производная равна нулю, может и не быть точкой экстремума. Например, в точке 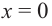
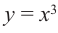
На отрезке непрерывности функция может иметь несколько критических точек, точек максимума и минимума. Существование экстремума в точке зависит от значения функции в данной точке и в точках, близких к данной, т. е. имеет смысл локального (местного) значения. Поэтому иногда используют термин локальный максимум и локальный минимум.
Достаточное условие существования экстремума
Пусть функция 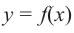
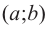
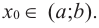
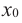
слева от точки
положительна, а справа — отрицательна, то точка
является точкой максимума.
слева от
отрицательна, а справа — положительна, то точка
является точкой минимума
с каждой стороны от точки
имеет одинаковые знаки, то точка
не является точкой экстремума.
Чтобы найти наибольшее (абсолютный максимум) или наименьшее (абсолютный минимум) значение функции, имеющей конечное число критических точек на отрезке, надо найти значение функции во всех критических точках и на концах отрезка, а затем из полученных значений выбрать наибольшее или наименьшее.
Соответствующие наибольшее и наименьшее значения функции 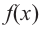
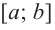
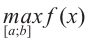
Ниже представлены примеры определения максимума и минимума в соответствии со знаком производной первого порядка.
Пример №5
Для функции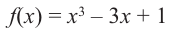
Решение: Для решения задания сначала надо найти критические точки. Для данной функции этими точками являются точки (стационарные), в которых производная равна нулю.
1. Производная функции:
2. Критические точки функции:
3. Точки 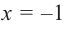
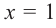
Проверим знак 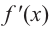
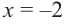
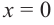
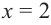

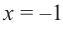
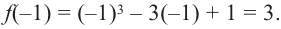
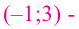
При 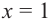
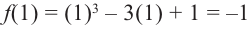
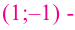
4. Используя полученные для функции 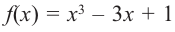
Пример №6
Найдите наибольшее и наименьшее значение функции 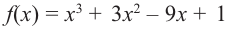
Решение: Сначала найдем критические точки.
Так как 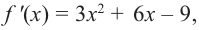
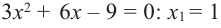
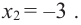
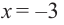
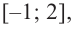
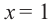
Из этих значений наименьшее — 4, наибольшее 12. Таким образом:
Пример №7
Найдите экстремумы функции
Решение: 1. Производная функции:
2. Критические точки:
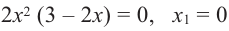
3. Интервалы, на которые критические точки делят область определения функции:
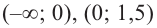
Проверим знак 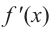
Для промежутка 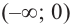
Для промежутка 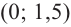
Для промежутка 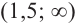
Используя полученную для функции 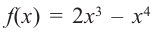
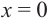
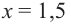
Пример №8
Найдите экстремумы функции
Решение: 1. Производная
2. Критические точки: для этого надо решить уравнение 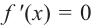
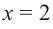
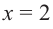
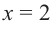
3. Промежутки, на которые критическая точка делит область определения функции: 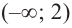
Определим знак 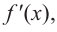
Для 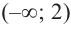
Для 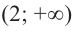
Пример №9
По графику функции производной 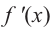
Решение:
Производная 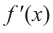
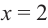
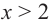
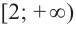
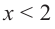
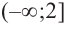
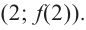
- Заказать решение задач по высшей математике
Построение графиков функции с помощью производной
Функция — многочлен определена и непрерывна на всей числовой оси.
Чтобы построить график функции- многочлен надо выполнить следующие шаги.
- Определите точки пересечения с осями координат.
- Найдите критические точки.
- Найдите промежутки возрастания и убывания функции.
- Найдите максимумы и минимумы.
- Постройте график.
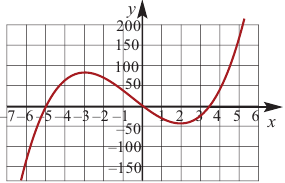
Пример:
Постройте график функции
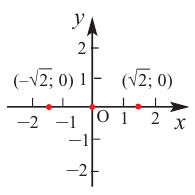
1) Точки пересечения с осями координат :
2) Критические точки ( точки, в которых производная равна нулю):
значит, точки 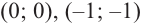
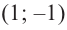
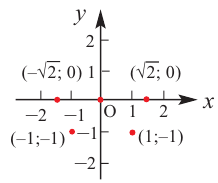
3) Промежутки возрастания и убывания. Экстремумы.
Критические точки 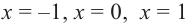
4) Используя полученную информацию, построим график функции.
Чтобы построить график рациональной функции надо выполнить следующие шаги.
- Найдите область определения.
- Найдите асимптоты (если они есть).
- Определите точки пересечения с осями координат.
- Найдите критические точки.
- Найдите промежутки возрастания и убывания и экстремумы.
- Постройте график.
Пример:
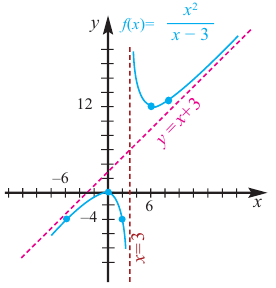
Постройте график функции
1) Область определения функции:
2) Асимптоты:
Прямая 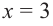
Так как степень многочлена в числителе больше степени многочлена в знаменателе, рациональная функция не имеет горизонтальной асимптоты. Однако, записав следующее:
условии 
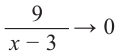
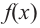
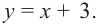
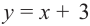
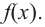
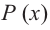
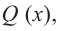
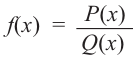
3) Точки пересечения с осями координат:
4) Критические точки:
5) Промежутки возрастания и убывания: в точке 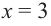
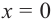
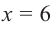
6) Построим график. Отметим на координатной плоскости точки 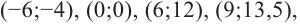
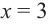
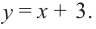
Обратите внимание! В области, близкой к точке 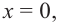
Задачи на экстремумы. Оптимизации
В реальной жизненной ситуации возникает необходимость выбора оптимального варианта и нахождения экстремумов определенной функции. Ежедневно, при решении проблем в различных областях, мы сталкиваемся с терминами наибольшая прибыль, наименьшие затраты, наибольшее напряжение, наибольший объем, наибольшая площадь и т.д. Большое экономическое значение в промышленности, при определении дизайна упаковки, имеет вопрос, как подобрать размеры упаковки с наименьшими затратами. Такого рода задания связаны с нахождением максимального или минимального значения величины. Задачи на нахождение максимального и минимального значения величины называются задачами на оптимизацию. Для решения данных задач применяется производная.
Замечание 1: На интервале 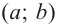
Замечание 2: В рассматриваемом интервале может быть одна стационарная точка: или точка максимума, или точка минимума. В этом случае, в точке максимума функция принимает наибольшее значение, а в точке минимума — наименьшее значение.
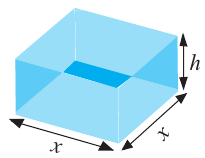
Пример 1. Максимальный объем. Фирма планирует выпуск коробки без крышки, с квадратным основанием и площадью поверхности 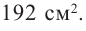
Решение:
Так как основанием коробки является квадрат, то ее объем можно вычислить по формуле 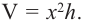
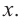
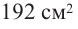
Тогда выразим 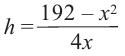
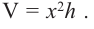
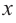
Теперь найдем область определения функции 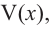
Понятно, что длина не может быть отрицательной, т. е. 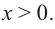
или 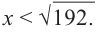
Найдем максимальное значение функции 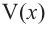
Для этого используем производную первого порядка:
При 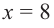
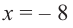
Однако. 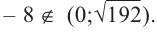
При 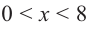
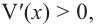
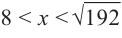
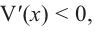
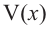
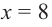
Если длина основания коробки будет 8 см, то высота будет равна
Значит, максимальный объем будет иметь коробка с размерами
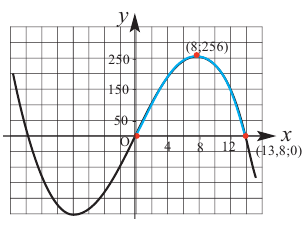
Построив при помощи графкалькулятора график функции 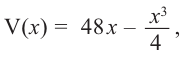
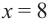
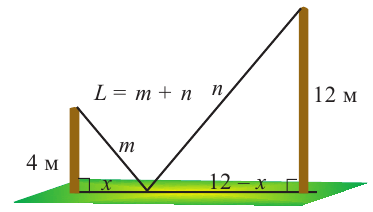
Пример 2. Минимальное потребление. Два столба высотой 4 м и 12 м находятся на расстоянии 12 м друг от друга. Самые высокие точки столбов соединены с металлической проволокой, каждая из которых, в свою очередь крепится на земле в одной точке. Выберите такую точку на земле, чтобы для крепления использовалось наименьшее количество проволоки.
Решение: 1) Изобразим рисунок, соответствующий условию задачи, и обозначим соответствующие данные на рисунке.
2) Аналитически выразим зависимость между переменными.
По теореме Пифагора:
зависимость функции 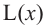
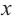
Производная функции
Найдем критические точки функции
Сравнивая значения функции 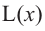
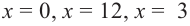
При решении задач на экстремумы обратите внимание на следующее!
1. Внимательно читайте условие. Сделайте соответствующий рисунок.
2. Задайте список соответствующих переменных и констант, которые менялись и оставались неизменными и какие единицы использовались. Если на рисунке есть размеры, обозначьте их.
3. Выберите соответствующий параметр 
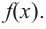
4. Полученные значения объясните экспериментально.
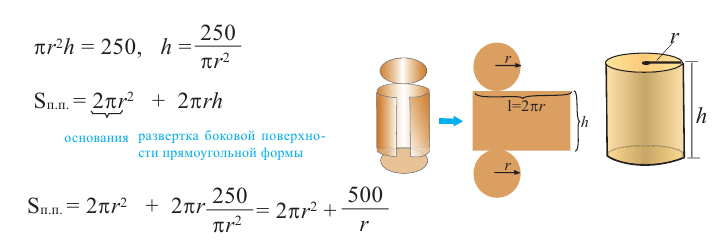
Пример: Минимальное потребление материала. Для мясных консервов планируется использовать банку в форме цилиндра объемом 250
a) Каких размеров должна быть банка, чтобы для ее изготовления использовалось как можно меньше материала?
b) Для круглого основания используется материал, цена 1 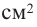
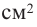
Решение: а) По условию задачи объем равен 250 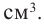
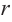
Для функции, выражающей площадь поверхности, область определения представляет собой незамкнутый интервал, и мы должны найти, при каком значении 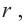
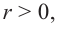
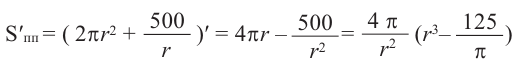
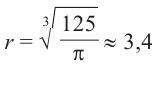
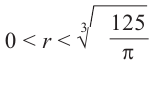
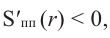
Значит,
Подставим значение 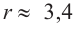
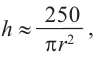
Итак, минимальные затраты на материал будет иметь банка цилиндрической формы с размерами 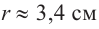
Размеры, при которых затраты на материал будут минимальными
- Приложения производной
- Производные высших порядков
- Дифференциал функции
- Дифференцируемые функции
- Касательная к графику функции и производная
- Предел и непрерывность функции
- Свойства функций, непрерывных в точке и на промежутке
- Предел функции на бесконечности
Александр Мельник
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Определение 1
Функцией, заданной на множестве $X$ и принимающей значения из множества $Y$ называют некую закономерность, по которой каждому элементу из множества $X$ соответствует лишь один и только один элемент из множества $Y$.
Из этого определения следует, что множество (область) значений функции — это те значения функции $y(x)$, которые она может принимать соответственно области её определения. Теперь перейдём к следующему определению.
Определение 2
Область (множество) значений функции на некотором рассматриваемом отрезке — это интервал значений, которые функция принимает на этом рассматриваемом отрезке.
Чаще всего в учебной литературе встречается термин «множество значений функции». Кратко его обозначают $E(f)$.
Как определить область значения функции
Для определения множества значений функции пользуются графическим методом, методом поисков минимума и максимума, вычислением производной и другими.
Определение множества значений функции графическим методом
Графический метод подразумевает построение графика функции и изучение этого графика. Этот метод наиболее удобен, если не известна какая-либо закономерность изменения функции $f(x)$, а есть только набор произвольных точек или собственно сам график.
Пример 1
Рисунок 1. Определение множества значений функции графическим методом
На данном рисунке область значений функции $y=f(x)$ равна $E(y)=3$, так как на протяжении всего отрезка функция $y$ не меняет своего значения и всегда равна $3$, тогда как область определения функции $D(y)=[0;3.5]$.
Скобки в данном случае для области определения функции необходимо использовать квадратные, так как обе точки закрашены, то есть включены в отрезок. В случае если точки не закрашены, они не включаются в отрезок и тогда применяются круглые скобки.
«Множество значений функции» 👇
Метод нахождения области значения функции через производную
Метод нахождения области значения функции через производную состоит в том, чтобы сначала оценить область её определения (то есть определить те значения, которые может принимать аргумент $x$, а затем осуществить процедуру нахождения самой производной. После этого осуществляют поиск значений $x$, при которых производная функции равна нулю и при которых производная не существует.
Рассмотрим пример нахождения области значений функции через производную.
Пример 2
Дана функция $f(x)=sqrt{16-x^2}$. Найдите область её значений.
Сначала определяем, какие значения может принимать $x$ для существования функции.
При значении $x^2>16$ под корнем получается отрицательное число, а это значит, что область определения функции от $[-4;4]$ включительно.
Теперь найдём производную функции:
$(sqrt{16-x^2})’=-frac{x}{sqrt{16-x^2}}$
Если в знаменателе производной нуль, то производной не существует, в данном случае это условие выполняется при $x=±4$.
Приравниваем производную к нулю и находим значения $x$. Производная данной функции принимает нулевое значение при $x=0$. Теперь подставляем найденные значения производной в нашу функцию, и получаем, что наименьшее значение функции — это $f(4)$ и $f(-4)$, при этих значениях функция равна нулю, а наибольшее значение $f(x)$ — при $x=0$, в этой точке функция равна $16$.
Метод поиска минимума и максимума
Метод поиска минимума и максимума основан на том, чтобы найти максимальное и и минимальное значение, которые функция принимает на изучаемой области.
Пример 3
Определите область значений функции:
$y=6-4sinx$
Проанализируем данную функцию. Так как минимальное значение синуса равно минус единице, а а максимальное — единице, то подставив эти значения получаем, что $max(f(x))=10$ при $x=frac{3π}{2}$, а минимум $min(f(x))=2$ при $x=frac{π}{2}$. Следовательно, множество значений, которые может принимать данная функция — $E(x)=[2;10]$.
Разница между областью значения и областью определения функции
Стоит обратить внимание, что область значений функции — не одно и то же с термином «область определения функции».
Определение 3
Область определения функции $D(y)$ — это диапазон таких значений переменной $x$, при которых существует функция $y(x)$.
Например, рассмотрим функцию $y(x)=x^2$. В данном случае область определения этой функции будет множеством вещественных (действительных) чисел $mathbb{R}$, а сама функция будет принимать значения только положительных действительных чисел $mathbb{R}^+$, так как вещественное число, возведённое в квадрат, не может давать отрицательное значение. То есть, в этом примере множество значений функции — это множество положительных вещественных чисел $mathbb{R}^+$.
Также имеют место случаи, когда область определения функции совпадает с областью значений.
В качестве иллюстрации можно рассмотреть функцию $y(x)=2x$. За аргумент $x$ данная функция может принимать любое действительное число из множества $mathbb{R}$, а значения, которые будет принимать сама функция — это удвоенные числа из множества всех действительных чисел. То есть, в данном случае областью значений $E(y)$ будет также всё множество вещественных чисел $mathbb{R}$.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Лекция 4. Применение производной к исследованию функций и построению графиков.
План
1. Возрастание и
убывание функции.
2. Экстремумы
функции.
3. Схема исследования функции и построения её
графика с помощью производной.
4. Решение задач
(Учебник: Ш.А.
Алимов Алгебра и начала математического анализа 10-11 класс глава IX §49, §50, §51, стр. 261-264, стр. 265-269, стр. 271-275)
1. Возрастание и
убывание функции.
Производная широко
используется для исследования функций, т.е. для изучения различных свойств
функций. Например, с помощью производной можно находить промежутки возрастания
и убывания функции, её наибольшее и наименьшее значения.
Рассмотрим применение
производной к нахождению промежутков возрастания и убывания функций.

производной функции положительны на некотором промежутке, т.е.
. Тогда угловой коэффициент касательной
к графику этой функции в каждой точке данного промежутка положителен.
Это означает, что касательная образует острый угол с осью Ox, и поэтому график функции на этом промежутке «поднимается», т.е.
функция возрастает (рис.120).
Если на некотором промежутке, то угловой коэффициент касательной
к графику функции
отрицателен.
Это означает, что
касательная образует тупой угол с осью Ox, и поэтому
график функции на этом промежутке «опускается», т.е. функция убывает (рис. 121).
Итак, если на промежутке, то функция
возрастает на этом промежутке.
Если на промежутке, то функция
убывает на этом промежутке.
При доказательстве
теорем о достаточных условиях возрастания или убывания функции используется теорема
Лагранжа.
Теорема Лагранжа. Если функция непрерывна на отрезке [a;b]
и дифференцируема на интервале (a;b),
то существует точка такая, что
. (1)
Доказательство
формулы (1) приводится в курсе высшей математики. Поясним геометрический смысл
этой формулы.
Проведём через
точки и
графика функции
прямую l и назовём эту прямую секущей. Угловой
коэффициент секущей равен .
Запишем формулу (1)
в виде . (2)
Согласно формуле
(2) угловой коэффициент касательной к графику функции в точке C с абсциссой c
(рис. 122) равен угловому коэффициенту секущей l, т.е. на
интервале (a;b) найдётся такая точка c, что в точке графика с абсциссой c касательная к
графику функции параллельна секущей. Сформулируем с помощью теоремы Лагранжа теорему
о достаточном условии возрастания функции.

функция дифференцируема на интервале (a;b) и
для всех
, то функция возрастает на интервале (a;b).
Пример 1.
Доказать, что
функция возрастает на промежутке
.
Доказательство:
Найдём производную:
.
Если , и поэтому данная функция возрастает на промежутке
.
Промежутки
возрастания и убывания функции часто называют промежутками монотонности
этой функции.
Правило
нахождения интервалов монотонности функции .
1. Находят
производную данной функции.
2. Находят точки, в
которых равна нулю или не существует, т.е. критические точки функции
.
3. Найденными
точками область определения функции разбивается на интервалы, на каждом из которых производная
сохраняет свой знак. Эти интервалы являются интервалами монотонности
(т.е. критические точки отмечаем на числовой прямой и определяем знак
производной в каждом интервале, подставив соответствующее значение xв формулу производной).
4. Исследуют знак на каждом из найденных интервалов.
Если на
рассматриваемом интервале , то на этом интервале
возрастает;
если же , то на таком интервале
убывает.
Пример 2.

интервалы монотонности функции .
Решение
Найдем производную:
.
Решая неравенство , т.е. неравенство
, находим интервалы возрастания:
.
Решая неравенство , т.е. неравенство
, находим интервал убывания
.
Ответ: возрастает;
убывает.
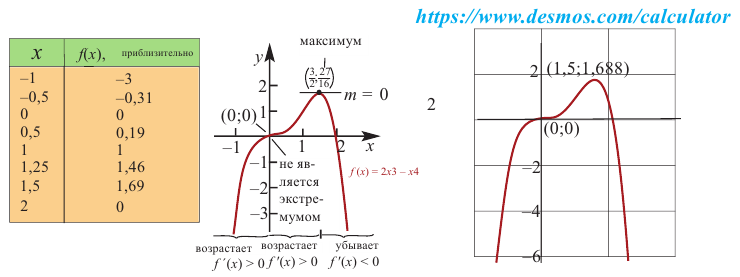
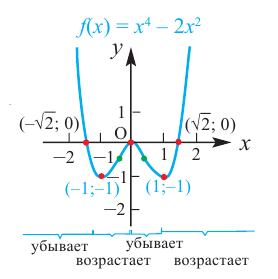
График функции изображен на рисунке 123. Из этого рисунка видно, что функция
возрастает не только на интервалах
, но и на промежутках
; убывает не только на интервале
, но и на отрезке
.
2. Экстремумы
функции.
На рисунке 123
изображён график функции . Рассмотрим окрестность точки x = 0, т.е.
некоторый интервал, содержащий эту точку. Как видно из рисунка, существует
такая окрестность точки x = 0, что наибольшее значение
функция в этой окрестности принимает в точке x = 0.
Например, на интервале (-1; 1) наибольшее значение, равное 0, функция принимает
в точке x = 0. Точку x = 0 называют
точкой максимума этой функции.
Аналогично точку x = 2 называют точкой минимума функции , так как функции в этой точке меньше её значения в любой точке
некоторой окрестности точки x = 2, например окрестности
(1,5; 2,5).
Точка называетсяточкой максимума функции
, если существует такая окрестность точки
, что для всех
из этой окрестности выполняется неравенство
.
 |
Например, точка является точкой максимума функции
, так как
и при всех значения
верно неравенство
(рис. 124).
Точка называетсяточкой минимума функции
, если существует такая окрестность точки
, что для всех
из этой окрестности выполняется неравенство
.
Например, точка является точкой минимума функции
, так как
при всех значениях
(рис. 125).
Точки минимума и
точки максимума называются точками экстремума. Экстремум –
значение функции в этих точках.
Рассмотрим функцию , которая определена в некоторой окрестности точки
и имеет производную в этой точке.
Теорема. Если — точка экстремума дифференцируемой функции
, то
.
Это утверждение
называют теоремой Ферма.
 |
Теорема Ферма имеет наглядный геометрический смысл: касательная к
графику функции в точке
, где
— точка экстремума функции
, параллельна оси абсцисс, и поэтому её угловой коэффициент
равен нулю (рис. 126).
Например, функция (рис.124) имеет в точке
максимум, её производная
. Функция
имеет минимум в точке
(рис. 125),
.
Отметим, что если , то этого недостаточно, чтобы утверждать, что
обязательно точка экстремума функции
.
Например, если . Однако точка x = 0 не является точкой
экстремума, так как функция возрастает на всей числовой оси (рис. 127).
Итак, точки
экстремума дифференцируемой функции нужно искать только среди корней уравнения , но не всегда корень этого уравнения является точкой экстремума.
Точки, в которых производная функции равна нулю, называют стационарными.
Заметим, что
функция может иметь экстремум и в точке, где эта функция не имеет производной.
Например, x = 0 – точка минимума функции не существует. Точки, в которых функция имеет производную, равную
нулю, или недифференцируема, называют критическими точками этой функции.
Таким образом, для
того чтобы точка была точкой экстремума функции
, необходимо, чтобы эта точка была критической точкой данной функции.
Приведём достаточные условия того, что стационарная точка является точкой
экстремума, т.е. условия, при выполнении которых стационарная точка есть точка
максимума или минимума функции.
 |
Теорема. Пусть функция дифференцируема на интервале (a; b),
, и
.
Тогда:
1) если при переходе через стационарную точку функции
её производная меняет знак с «плюса» на «минус», т.е.
слева от точки
и
справа от точки
, то
— точка максимума функции
(рис. 128);
2) если при переходе через стационарную точку функции
её производная меняет знак с «минуса» на «плюс», то
— точка минимума функции
(рис. 129);
Если же не меняет знак в окрестности точки
, то данная функция не имеет экстремума в точке
.
Правило
нахождения экстремумов функции .
1. Находят
производную данной функции.
2. Находят все
критические точки из области определения функции.
3. Устанавливают
знаки производной функции при переходе через критические точки и выписывают
точки экстремума.
4. Вычисляют
значения функции в каждой точке экстремума.
Пример 3
Найти точки
экстремума функции .
Решение
1. Найдём
производную:
2. Найдём все
критические точки из области определения функции. Решим уравнение .
.
3. Установим знаки производной функции при переходе через критические
точки и выпишем точки экстремума. Для этого отметим полученные
значения на числовой прямой. Точки и
разделили область определения функции
на три интервала. Вычислим знак производной в каждом из этих
интервалов:
;
;
.
Так как при
переходе через точку знак производной не меняется, то эта точка не является точкой
экстремума.
При переходе через
точку производная меняет знак с «-» на «+». Поэтому
— точка минимума.
Ответ: — точка минимума.
Пример 4
Найти точки
экстремума функции и значения функции в этих точках.
Решение
1. Найдём
производную: .
2. Найдём
критические точки.
или
– не существует
.
3. Установим знаки производной функции при переходе через критические
точки и выпишем точки экстремума. Для этого отметим
полученные значения на числовой прямой. Точки и
разделили область определения функции
на три интервала. Вычислим знак производной в каждом из этих
интервалов:
;
;
.
При переходе через
точку производная меняет знак с «+» на «-». Поэтому
— точка максимума. При переходе через точку
производная меняет знак с «-» на «+», поэтому
— точка минимума.
4. Вычислим значения функции в каждой точке экстремума.
Значение функции в
точке максимума равно , а в точке минимума
.
Ответ: — максимум,
. – минимум.
3. Схема
исследования функции и построения её графика с помощью производной.
Примерная
схема исследования функции:
1. Найти область
определения функции (если возможно, то множество значений).
2. Выяснить, не
является ли функция чётной, нечётной, периодической.
3. Найти точки
пересечения графика функции с осями координат (если это не вызывает
затруднений).
4. Найти асимптоты
графика функции (если это необходимо, только для функций, которые имеют точки
разрыва, т.е. не являются непрерывными).
5. Найти промежутки
монотонности функции и её экстремумы.
6*. Найти
промежутки выпуклости графика функции и точки перегиба (применение производной
второго порядка).
7. Вычислить
координаты дополнительных точек (если это необходимо).
В зависимости от
сложности функции некоторые пункты данной схемы могут быть пропущены.
Пример 5
Построить график
функции .
Решение
1.
2. Исследуем на
чётность: . Функция не является ни чётной, ни нечетной, т.е. общего вида.
3. Пересечение с
осью Ox: ,
. Таким образом, получили две точки
.
Пересечение с осью Oy: .
4. С помощью
производной найдём промежутки монотонности этой функции и её точки экстремума.
Производная равна . Найдем стационарные точки:
,
откуда .
Для определения
знака производной разложим квадратный трёхчлен на множители:
.
Производная
положительна на промежутках , следовательно, на этих промежутках функция возрастает.
При производная отрицательна, следовательно, на интервале
функция убывает.
Точка является точкой максимума, так как слева от этой точки функция
возрастает, а справа убывает. Значение функции в этой точке равно .
Точка является точкой минимума, так как слева от этой точки функция убывает,
а справа возрастает; её значение в точке минимума равняется .
Результаты
исследования представим в следующей таблице:
 |
5.
Для более точного построения графика найдём значения функции ещё в двух точках:

Используя
результаты исследования, построим график функции (рис. 132).
Пример 6. Исследуйте и постройте графики функций:
а) ;б)
.
|
№ |
План исследования |
Применение |
плана |
|
шага |
Функции |
а) |
б) |
|
1 |
Находим область |
|
|
|
2 |
Исследуем функцию |
|
|
|
3
|
Находим нули |
|
|
|
4 |
Находим производную |
|
|
|
5
|
Находим промежутки |
х=0 – не |
х=0 – точка |
|
6 |
Находим предел |
|
|
|
7
|
Строим эскиз |
4. Задания для
самостоятельного решения
Задача 1 (1 балл)
Найдите промежутки
убывания и возрастания функции: .
В ответе укажите
промежуток убывания.
Задача 2 (2 балла)
Найдите промежутки
убывания и возрастания функции: .
1. при убывает; при
возрастает
2. при убывает; при
возрастает
3. при убывает; при
возрастает
4. при возрастает
В ответе укажите
номер с правильным ответом.
Задача 3 (3 балла)
Найдите промежутки
убывания функции .
Задача 4 (2 балла)
Найдите точку
минимума функции .
Задача 5 (2 балла)
Найдите точку
максимума функции .
Вспомним кратко основные определения функции в математике.
Функция — это зависимость переменной « y » от
независимой переменной « x ».
Функцию можно задать через формулу (аналитически). Например:
у = 2x
- « x » называют независимым аргументом функции;
- « y » зависимой переменной или значением функции.
Вместо « x » (аргумента функции) в формулу «у = 2x» подставляем произвольные числовые значения
и по заданной формуле вычисляем
значение « y ».
Подставим несколько числовых значений вместо « x » в формулу «у = 2x» и запишем результаты в таблицу.
| x | y = 2x | ||||||
|---|---|---|---|---|---|---|---|
| x = −2 | у = 2 · (−2) = −4 | ||||||
| x = 0 | y = 2 · 0 = 0 | ||||||
x =
|
y = 2 ·
= 1 |
||||||
| x = 3 | y = 2 · 3 = 6 |
Запомните!
Область определения функции — это множество числовых значений, которые можно подставить вместо « x » (аргумента функции).
Обозначают область определения функции как:
D(y)
Вернемся к нашей функции «у = 2x» и найдем её область определения.
Посмотрим ещё раз на таблицу функции «y = 2x», где
мы подставляли произвольные числа вместо « x », чтобы найти « y ».
| x | y = 2x | ||
|---|---|---|---|
| −2 | −4 | ||
| 0 | 0 | ||
|
1 | ||
| 3 | 6 |
Так как у нас не было никаких ограничений на числа, которые можно подставить вместо « x », можно утверждать,
что вместо « x » мы могли подставлять любое действительное число.
Другими словами, вместо « x » можно подставить любые числа, например:
- −2
- 0
- 10
- 30,5
- 1 000 000
- и так далее…
Запомните!
Областью определения функции называют множество чисел,
которые можно подставить вместо « x ».
В нашей функции «у = 2x» вместо « x »
можно подставить любое число, поэтому область определения функции «у = 2x» — это любые действительные числа.
Запишем область определения функции «у = 2x» через математические обозначения.
у = 2x
D(y): x — любое действительное число
Ответ выше написан словами без использования специального математического языка. Заменим лишние слова на
математические символы.
Для этого вспомним понятие числовой оси.
Заштрихуем область на числовой оси, откуда можно брать значения для « x » в функции «у = 2x».
Так как в функции
«у = 2x» нет ограничений для « x »,
заштрихуем всю числовую ось от минус бесконечности «−∞» до плюс бесконечности
«+∞».
Запишем результат по правилам записи неравенств.
D(y): x ∈ (−∞ ; +∞)
Запись выше читается как: « x » принадлежит промежутку от минус бесконечности
до плюс бесконечности.
Запишем окончательный ответ для области определения функции.
Ответ:
D(y): x ∈ (−∞ ; +∞)
По-другому промежуток
« x ∈ (−∞ ; +∞) » можно записать
как
«x ∈ R».
Читается «x ∈ R» как: « x » принадлежит всем действительным числам».
Записи « x ∈ (−∞ ; +∞) » и
«x ∈ R» одинаковы по своей сути.
Область определения функции с дробью
Разберем пример сложнее, когда в задании на поиск области определения функции есть дробь с « x » в знаменателе.
Разбор примера
Найдите область определения функции:
Задание «Найдите область определения функции» означает, что нам нужно определить все числовые значения, которые может принимать « x »
в функции
« f(x) = ».
По законам математики из школьного курса мы помним, что на ноль делить нельзя.
Иначе говоря,
знаменатель (нижняя часть дроби) не может быть равен нулю.
Переменная « x » находится в знаменателе функции «f(x) = ».
Так как на ноль делить нельзя, запишем, что знаменатель не равен нулю.
x + 5 ≠ 0
Решим полученное линейное уравнение.
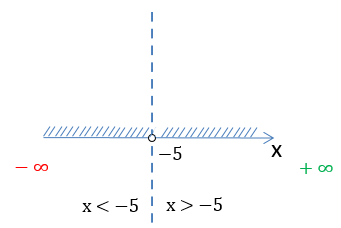
Получается, что « x » может принимать любые числовые значения кроме «−5».
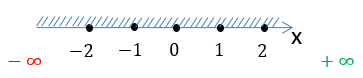
На числовой оси заштрихуем все доступные значения для « x ».
Число «−5» отмечено
«пустой»
точкой на числовой оси, так как не входит в область допустимых значений.
Запишем заштрихованную область на числовой оси через знаки неравенства.
Запишем промежутки через математические символы. Так как число «−5» не входит
в область определения функции, при записи ответа рядом с ним будет стоять
круглая скобка.
Вспомнить запись ответа через математические символы можно в уроке
«Как записать ответ неравенства».
x ∈ (−∞ ; −5) ∪ (−5 ; +∞)
Запишем окончательный ответ для области определения функции
«f(x) = ».
Ответ:
D(y): x ∈ (−∞ ; −5) ∪ (−5 ; +∞)
Область определения функции с корнем
Рассмотрим другой пример. Требуется определить область определения функции, в которой содержится квадратный корень.
Разбор примера
Найти область определения функции:
y = √6 − x
Из урока «Квадратный корень» мы помним,
что подкоренное выражение корня чётной степени должно быть больше или равно нулю.
Найдём, какие значения может принимать « x » в функции
«у = √6 − x».
Подкоренное выражение
«6 − x» должно быть больше или равно нулю.
6 − x ≥ 0
Решим линейное неравенство по правилам урока «Решение линейных неравенств».
6 − x ≥ 0
−x ≥ −6 | ·(−1)
x ≤ 6
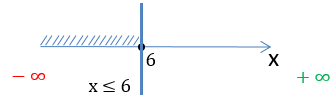
Запишем полученный ответ, используя числовую ось и математические символы. Число «6» отмечено
«заполненной»
точкой на числовой оси, так как входит в область допустимых значений.
x ∈ (−∞ ; 6]
Запишем окончательный ответ для области определения функции
«y = √6 − x» .
Так как число «6» входит
в область определения функции, при записи ответа рядом с ним будет стоять
квадратная скобка.
Ответ:
D(y): x ∈ (−∞ ; 6]
Правило для определения области определения функции
Запомните!
Чтобы найти область определения функции нужно проверить формулу функции по двум законам школьного курса математики:
- на ноль делить нельзя (другими словами, знаменатели дробей с « x » не должны быть равны нулю);
- подкоренные выражения корней чётной степени должны быть больше или равны нулю.
При нахождении области определения функции необходимо всегда задавать себе два вопроса:
- есть ли в функции дроби со знаменателем, в котором есть « x »?
- есть ли корни четной
степени с « x »?
Если на оба вопроса вы получаете отрицательный ответ, то область определения функции — это все действительные числа.
Рассмотрим пример поиска области определения функции с корнем и дробью.
Разбор примера
Найдите область определения функции:
Идем по алгоритму. Задаём себе первый вопрос, есть ли в функции дробь с « x » в знаменателе. Ответ: да, есть.
В функции «
f(x) = √x + 3 +
»
есть дробь «
»,
где « x » расположен в знаменателе. Запишем условие, что знаменатель
« x 2 − 9 »
не может быть равен нулю.
Решаем квадратное уравнение через
формулу квадратного уравнения.
x1;2 =
x2 − 9 ≠ 0
x1;2 =
| −0 ± √02 − 4 · 1 · (−9) |
| 2 · 1 |
x1;2 ≠
x1;2 ≠
x1;2 ≠
x1;2 ≠ ±3
Запомним полученный результат. Задаем себе
второй
вопрос.
Проверяем, есть ли в формуле функции
«
f(x) = √x + 3 +
»
корень четной степени.
В формуле есть квадратный корень «
√x + 3
».
Подкоренное выражение «x + 3»
должно быть больше или равно нулю.
x + 3 ≥ 0
Решим линейное неравенство.
x + 3 ≥ 0
x ≥ −3
Объединим полученные ответы по обоим вопросам:
- знаменатель дроби
«
» не равен нулю ; - подкоренное выражение «
√x + 3
» должно быть больше или равно нулю.
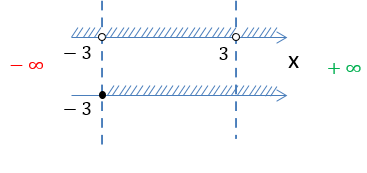
Объединим все полученные результаты на числовых осях.
Сравнивая полученные множества, выберем только те промежутки, которые удовлетворяют обоим условиям.
Выделим красным заштрихованные промежутки, которые совпадают на обеих числовых осях.
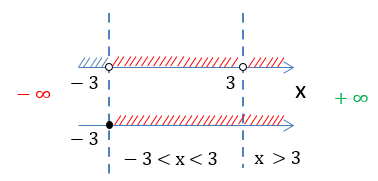
Обратим внимание, что числа «−3» и «3» отмечены «пустыми» точками и не входят в итоговое решение.
Получаем два числовых
промежутка «−3 < x < 3» и «x > 3», которые являются областью определения функции
«f(x) = √x + 3 + ».
Запишем окончательный ответ.
Ответ:
D(y): x ∈ (−3 ; 3) ∪ (3 ; +∞)
Примеры определения области определения функции
Разбор примера
Найти область определения функции:
y = 6√x +
5√1 + x
Для поиска области определения функций задаем себе
первый вопрос.
Есть ли знаменатель, в котором содержится « x »?
Ответ: в формуле функции
«y = 6√x +
5√1 + x»
нет дробей.
Задаем
второй вопрос.
Есть ли в функции корни четной степени?
Ответ: в функции есть корень шестой степени:
«6√x».
Степень корня — число «6». Число «6» — чётное,
поэтому подкоренное выражение корня «6√x»
должно быть больше или равно нулю.
x ≥ 0
В формуле функции «y = 6√x +
5√1 + x»
также есть корень пятой степени
«5√1 + x
».
Степень корня «5» — нечётное число, значит, никаких ограничений на подкоренное выражение
«1 + x»
не накладывается.
Получается, что единственное ограничение области определения функции
«y = 6√x +
5√1 + x»
— это ограничение подкоренного выражения
«6√x».
x ≥ 0
Нарисуем область определения функции на числовой оси и запишем ответ.
Ответ:
D(y): x ∈ [0 ; +∞)
Разбор примера
Найдите область определения функции:
Есть ли в функции знаменатель, в котором содержится « x »? В заданной функции подобных знаменателей два.
Выделим знаменатели с « x » красным цветом.
Запишем условие, что каждый из знаменателей не должен быть равен нулю.
| √x + 2 ≠ 0 | |
| x2 − 7x + 6 ≠ 0 |
Обозначим их номерами «1» и
«2» и решим каждое уравнение отдельно.
| √x + 2 ≠ 0 (1) | |
| x2 − 7x + 6 ≠ 0 (2) |
Решаем первое уравнение.
√x + 2 ≠ 0 (1)
Если значение квадратного корня
«√x + 2 ≠ 0» не должно быть равно нулю,
значит, подкоренное выражение
«x + 2 ≠ 0»
также не должно быть равно нулю.
√x + 2 ≠ 0 (1)
x + 2 ≠ 0
x ≠ −2
Теперь решим уравнение под номером «2», используя
формулу квадратного уравнения.
x1;2 =
x2 − 7x + 6 ≠ 0 (2)
x1;2 =
| −(−7) ± √(−7)2 − 4 · 1 · 6 |
| 2 · 1 |
x1;2 =
x1;2 =
x1;2 =
Запишем все полученные ответы в порядке возрастания вместе под знаком системы, чтобы их не забыть.
Знаменатели с « x »
мы проверили. Настала очередь
проверить
формулу функции
на
наличие корней четной степени .
В формуле функции
«f(x) =
+
»
есть два корня
«√x − 4» и
«√x + 2». Их подкоренные
выражения должны быть больше или равны нулю.
Решим полученную
систему неравенств.
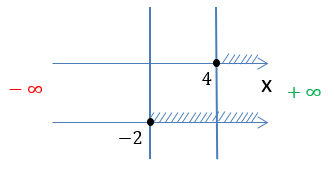
Нарисуем полученные решения на числовой оси. Выберем заштрихованный промежуток, который есть на обеих числовых осях.
Выпишем результат решения системы неравенств.
x ≥ 4
Объединим в таблицу ниже полученные ответы по обеим
проверкам:
- проверка, что знаменатели
дробей
с « x »
не равны нулю; - проверка, что
подкоренные выражения корней четной степени должно быть больше или равны нулю.
| Условие проверки | Результат |
|
Результат проверки, что знаменатели дробей с « x » не равны нулю |
|
|
Результат проверки, что подкоренные выражения должно быть больше или равны нулю |
x ≥ 4 |
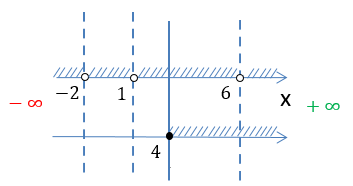
Нарисуем полученные результаты проверок на числовых осях, чтобы определить, какая заштрихованная область удовлетворяет
всем полученным условиям.
Запишем окончательный ответ для области определения функции
«f(x) =
+
»
с использованием математических символов.
Ответ:
D(y): x ∈ [4 ; 6) ∪ (6; +∞)
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
17 декабря 2016 в 18:02
Татьяна Цыганова
Профиль
Благодарили: 0
Сообщений: 1
Татьяна Цыганова
Профиль
Благодарили: 0
Сообщений: 1
Найти ОДЗ функции у=?(р1+р2х+x2)
Я не могу понять за какое число воспринимать p1, p2
0
Спасибо
Ответить
17 декабря 2016 в 19:10
Ответ для Татьяна Цыганова
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
x2 + p2x + p1 ? 0.
0
Спасибо
Ответить
24 февраля 2016 в 20:29
Влад Алексеев
Профиль
Благодарили: 0
Сообщений: 1
Влад Алексеев
Профиль
Благодарили: 0
Сообщений: 1
Постройте график функции y=-
. Укажите область определения функции
0
Спасибо
Ответить
25 февраля 2016 в 8:10
Ответ для Влад Алексеев
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Область определения функции: знаменатель не равен 0.
x+1?0
x?-1
Графиком является гипербола, смещеная влево относительно оси Y.
0
Спасибо
Ответить
5 февраля 2018 в 14:30
Ответ для Влад Алексеев
Кирилл Косован
Профиль
Благодарили: 0
Сообщений: 1
Кирилл Косован
Профиль
Благодарили: 0
Сообщений: 1
0
Спасибо
Ответить
11 февраля 2018 в 15:44
Ответ для Влад Алексеев
Татьяна Мирная
Профиль
Благодарили: 0
Сообщений: 1
Татьяна Мирная
Профиль
Благодарили: 0
Сообщений: 1
у=-
0
Спасибо
Ответить
7 октября 2015 в 21:21
Катерина Яроцкая
Профиль
Благодарили: 0
Сообщений: 1
Катерина Яроцкая
Профиль
Благодарили: 0
Сообщений: 1
Помогите найти область определения функции
0
Спасибо
Ответить
12 сентября 2016 в 15:59
Ответ для Катерина Яроцкая
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
К сожалению, картинка не отражается.
0
Спасибо
Ответить

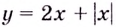
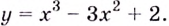
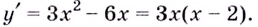
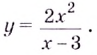
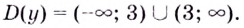
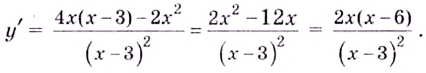
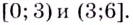
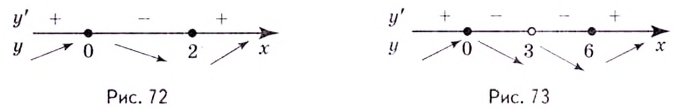
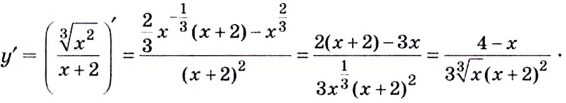
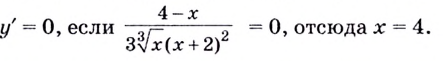
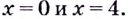
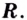
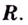
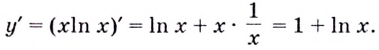
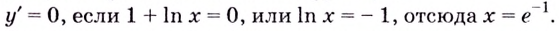
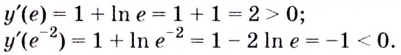
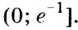
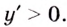
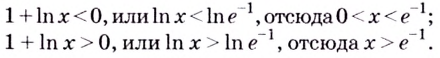
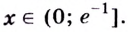
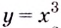
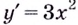
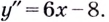
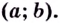
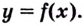
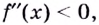 то кривая выпуклая; если
то кривая выпуклая; если 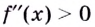 — кривая вогнутая;
— кривая вогнутая;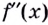 меняет знак при переходе через точку
меняет знак при переходе через точку 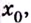 то точка
то точка 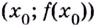 является точкой перегиба кривой
является точкой перегиба кривой 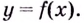
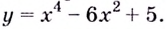
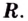
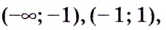
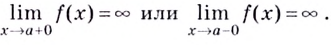
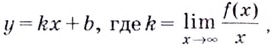
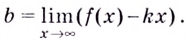
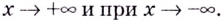
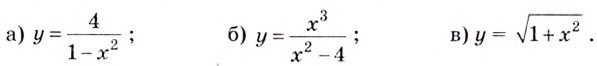
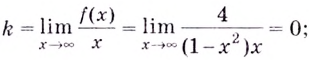
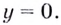
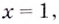
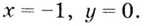
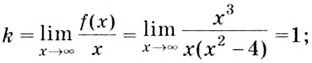
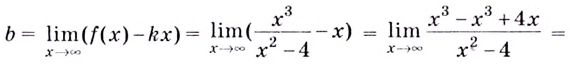
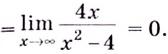
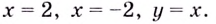
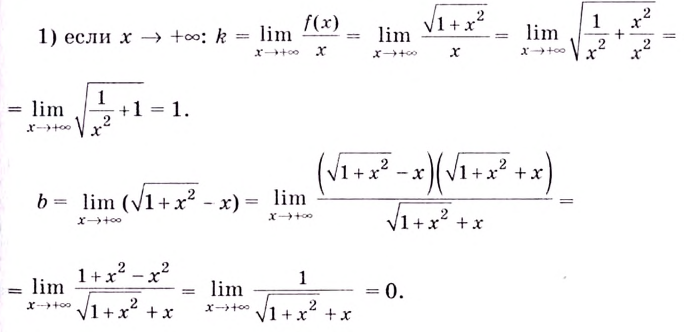
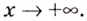
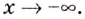
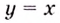
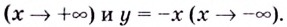
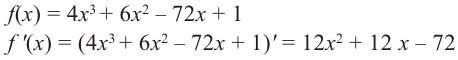
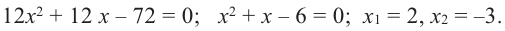

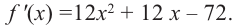
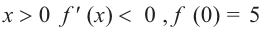
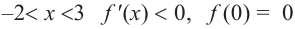
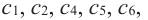
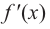 слева от точки
слева от точки 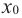 положительна, а справа — отрицательна, то точка
положительна, а справа — отрицательна, то точка 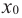 является точкой максимума.
является точкой максимума.