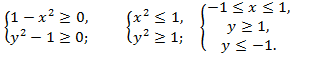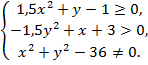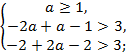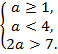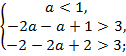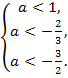Функции нескольких переменных (фнп)
1. Фнп, их определение, обозначение и область определения
1.
Переменная
называется функцией
многих
(нескольких)
переменных
(аргументов)
,
если каждой системе значений
из области их изменения соответствует
одно или несколько значений
.
Функциональная
зависимость
от
символически обозначается
,
где
после символа функции в скобках
указываются все переменные, от которых
зависит данная функция.
В
частном случае:
2.
Если каждой паре независимых друг от
друга чисел (х, у) из некоторого множества
по какому-либо правилу ставится в
соответствие одно или несколько значений
переменной z,
то переменная z
называется функцией
двух переменных.
3.
Если каждой системе значений
соответствует одно значение
,
то функция называется однозначной,
а если более одного, то – многозначной.
Частное
значение
функции
при
обозначается
.
Например, если
,
то
.
Геометрически:
—
каждая система значений двух переменных
изображается точкой на плоскости, а
функция двух переменных
— некоторой поверхностью в пространстве;
—
система значений трех переменных
изображается точкой в пространстве
(абсцисса, ордината, аппликата).
Система
значений четырех и большего числа
переменных не имеет геометрического
изображения. Однако в целях общности,
для упрощения записей и рассуждений:
4.
систему значений любого числа n
переменных
называют точкой
n-мерного
пространства (
)
,
а функцию
,
зависящую от n
переменных
называют функцией точки n—мерного
пространства
.
5.
Областью
определения
функции называется совокупность всех
точек, в которых она имеет определенные
действительные значения ( существует).
Геометрически:
—
область определения функции двух
переменных
представляет некоторую совокупность
точек плоскости;
—
а для функции трех переменных
трех переменных – некоторую совокупность
точек пространства.
ФНП
может быть задана аналитически (формулой),
геометрически (для функции двух
переменных) и таблицей.
Примеры.
1.Вычислить
частное значение функции:
а)
при
б)
в
2.Построить
область изменения переменных
и
,
заданную неравенствами:
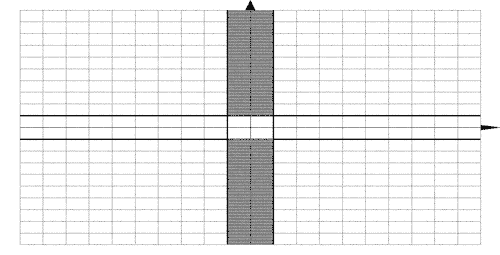
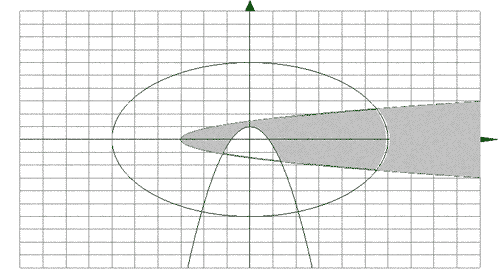
а)
,
.
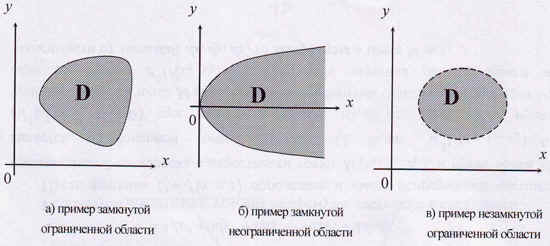
Этим
неравенствам удовлетворяют координаты
каждой точки, находящейся внутри и на
границе прямоугольника, стороны которого
лежат на прямых
,
.
Этот прямоугольник и есть область
изменения переменных
и
(рис. а).
Такая область,
в которую входит и ее граница, называют
замкнутой.
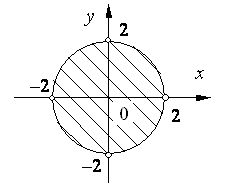
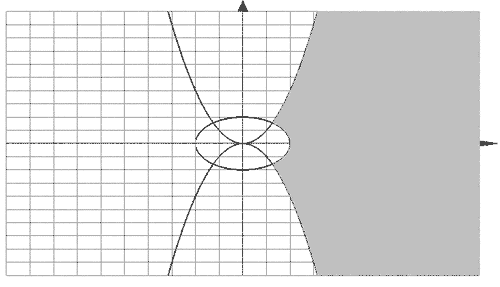
б)
.
Данная
область – совокупность всех точек,
лежащих внутри эллипса
.
Область открытая (рис.
б).
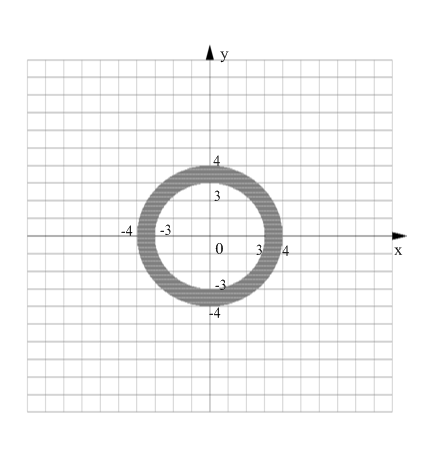
в)
.
Данная
область – круговое кольцо, ограниченное
окружностями
и
с общим центром в начале координат и
радиусами, равными 2 и 3. Область замкнутая
(рис. в).
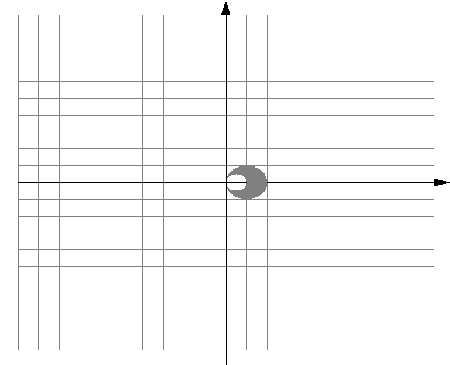
г)
.
Открытая
область, ограниченная биссектрисой
первого координатного угла и осью
абсцисс (рис.
г).
3.Найти
область определения функций:
а)
.
.
Геометрическое изображение этой функции
(график) – это плоскость, пересекающая
координатные оси в точках
,
и
.
б)
.
Из
условия, что знаменатель не должен
обращаться в нуль:
находим
и
одновременно. Отсюда: область определения
данной функции – вся числовая плоскость,
за исключением точки
.
в)
.
Из
условия, что подкоренное выражение быть
неотрицательным:
находим
.
Отсюда: область определения данной
функции – круг с центром в точке
и радиусом
.
(Внутри круга подкоренное выражение
положительно, на его границе – равно
нулю, а вне круга – отрицательно.)
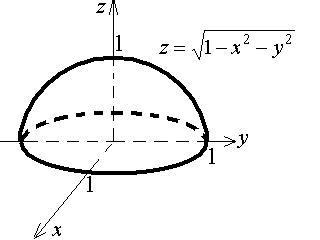
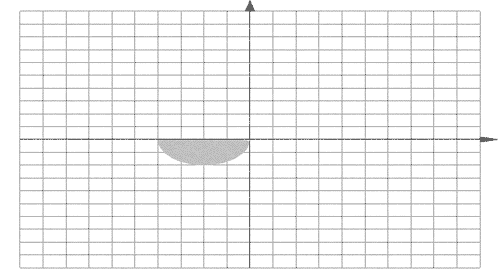
Графическим
изображением данной функции является
полусфера, расположенная над плоскостью
хОу (рис.2).
Рис.
2.
в)
.
Область
определения этой функции находим из
условия
.
Точки, удовлетворяющие этому неравенству,
лежат внутри I
и III
квадрантов.
г)
.
Область
определения этой функции – вся числовая
плоскость, за исключением прямой
.
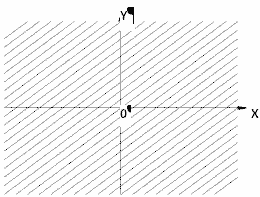
е)
.
Область
определения этой функции – совокупность
значений
и
,
удовлетворяющих неравенствам
.
На плоскости хОу эта область представляет
собой полосу, ограниченную параллельными
прямыми
и
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
17.09.201958.37 Кб26.doc
- #
Решение примеров с областью определения функции двух переменных
Содержание:
- Функции нескольких переменных: основные определения
- Экстремум функции нескольких переменных
-
Как найти область определения функции многих переменных — подробная инструкция
- Область определения функции двух переменных с корнем n-й степени
- Область определения степенной функции двух переменных, если показатель степени является целым числом
- Область определения степенной функции двух переменных, если показатель степени является дробным числом
- Область определения логарифмической функции двух переменных
- Область определения тригонометрических функций двух переменных
- Область определения обратных тригонометрических функций двух переменных
- Область определения дроби как функции двух переменных
- Область определения линейной функции двух переменных
- Примеры решения задач
Функции нескольких переменных: основные определения
При условии, что для любой из пар (х, у), являющихся значениями пары переменных х, у из какого-то множества D, существует единственное значение переменной z, то данная z называется функцией пары переменных х, у, определенной в области D. При этом множество D представляет собой область определения функции z.
Обозначением функции пары переменных является следующее соотношение:
z = f(x, y)
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Здесь f играет роль символа соответствия.
Геометрический смысл области определения D заключается в том, что D представляет собой какой-то участок на плоскости Оху. Эта область ограничена линиями, принадлежащими, либо не принадлежащими ей.
В том случае, когда функция записана в виде некой формулы без четкого указания на D, имеется в виду, что D включает в себя множество любых значений для переменных, при которых данная формула рассматриваемой функции обладает смыслом.
С целью дальнейшего рассмотрения темы введем некоторые обозначения:
Записи функций пары переменных имеют следующий вид: (zleft( {x,y} right), fleft( {x,y} right), gleft( {x,y} right), hleft( {x,y} right), Fleft( {x,y} right)).
Аргументы обозначают в этом случае таким образом: x, y, t
Малые приращения переменных x, y, z, соответствуют таким значениям: (Delta x, Delta y, Delta z).
Обозначение определителя: D
Заметим, что определение для функции одной переменной можно достаточно просто распространить на случаи, когда имеется два или более аргумента. Если рассматривается функция пары переменных, то предполагается множество пар (x, y), которые упорядочены, а их числовые значения взяты из множеств (x in X, y in Y).
При наличии закономерности, предусматривающей лишь одно значение z в виде числа для каждой пары (х, у), можно заключить, что задана функция двух переменных. Обозначением подобной функции является следующие примеры выражений:
(z = zleft( {x,y} right), z = fleft( {x,y} right), z = Fleft( {x,y} right)) и другие.
Аналогично можно определить функцию n переменных.
Если имеется некая функция z = f(x, y), то для любых пар (х, у) имеется возможность изобразить точку с определенными координатами, к примеру, М (х, у, z). При этом z = f(x, y). Множество рассматриваемых точек носит название графика функции z = f(x, y). В большинстве случаев график имеет вид определенной поверхности.
На графике область определения представляет собой плоскость ХОУ полностью, либо частично. Например, дана функция:
(z = — frac{A}{C}x — frac{B}{C}y — frac{D}{C})
В данном случае, область определения этой функции соответствует всей координатной плоскости ХОУ. Это объясняется существованием значения z для любой из точек (х, у).
Подобный случай не является единственным. Бывают и другие варианты. Введем понятие области определения.
Областью определения, либо областью существования, функции пары переменных z=f(x, y) называют совокупность пар (x, y), которые соответствуют значениям переменных х и у, а также определяют рассматриваемую функцию.
Рассмотрим характеристики такой функции. Разберем понятия ее предела и непрерывности.
Окрестность точки, расположенной на плоскости, представляет собой какой-либо круг, центральная точка которого совпадает с этой точкой.
Окрестность точки, расположенной в пространстве, представляет собой какой-либо шар, центральная точка которого совпадает с этой точкой.
Функция пары переменных z = f(x, y) является непрерывной в некой точке M0(x0; y0) при условии, что:
Рассмотрим пример функции:
(z = frac{1}{2x^{2} + y^{2}})
Заметим, что данная функция не прерывается в какой-либо точке на плоскости. Исключением в этом случае является начало координат, где можно наблюдать бесконечный разрыв функции.
Непрерывная функция в заданной области является такой функцией, которая не прерывается в любой точке, принадлежащей рассматриваемой области.
При рассмотрении функций более одной переменной следует познакомиться с понятием частной производной.
Частная производная первого порядка является производной функции по какой-то одной из переменных при фиксированных других переменных.
В качестве примера рассмотрим функцию пары переменных:
(z = fleft( {x,y} right))
В этом случае можно найти частные производные по переменной х и по переменной у, которые следует обозначить таким образом:
(largefrac{{partial z}}{{partial x}}normalsize = largefrac{{partial f}}{{partial x}}normalsize = {z’_x} = {f’_x},;;largefrac{{partial z}}{{partial y}}normalsize = largefrac{{partial f}}{{partial y}}normalsize = {z’_y} = {f’_y})
Частные производные второго порядка определяют следующим способом:
(largefrac{partial }{{partial x}}normalsizeleft( {largefrac{{partial f}}{{partial x}}}normalsize right) = largefrac{{{partial ^2}f}}{{partial {x^2}}}normalsize = {f»_{xx}},;; largefrac{partial }{{partial y}}normalsizeleft( {largefrac{{partial f}}{{partial y}}}normalsize right) = largefrac{{{partial ^2}f}}{{partial {y^2}}}normalsize = {f»_{yy}},)
(largefrac{partial }{{partial y}}normalsizeleft( {largefrac{{partial f}}{{partial x}}}normalsize right) = largefrac{{{partial ^2}f}}{{partial y,partial x}}normalsize = {f»_{xy}},;; largefrac{partial }{{partial x}}normalsizeleft( {largefrac{{partial f}}{{partial y}}}normalsize right) = largefrac{{{partial ^2}f}}{{partial x,partial y}}normalsize = {f»_{yx}}.)
В том случае, когда смешанные частные производные представляют собой непрерывные функции, отсутствует зависимость между этими производными и порядком дифференцирования:
(largefrac{{{partial ^2}f}}{{partial y,partial x}}normalsize = largefrac{{{partial ^2}f}}{{partial x ,partial y}}normalsize)
Существуют правила, согласно которым дифференцируют сложную функцию пары переменных. Представим, что выполняется следующее условие:
(fleft( {x,y} right) = gleft( {hleft( {x,y} right)} right))
Здесь g определена, как функция одной переменной h.
Тогда частные производные соответствуют:
(largefrac{{partial f}}{{partial x}}normalsize = g’left( {hleft( {x,y} right)} right)largefrac{{partial h}}{{partial x}}normalsize,;;largefrac{{partial f}}{{partial y}}normalsize = g’left( {hleft( {x,y} right)} right)largefrac{{partial h}}{{partial y}}normalsize.)
Предположим, что выполняется следующее условие:
(hleft( t right) = fleft( {xleft( t right),yleft( t right)} right))
В таком случае, вычисление производной выполняют, согласно формуле:
(h’left( t right) = largefrac{{partial f}}{{partial x}}frac{{dx}}{{dt}}normalsize + largefrac{{partial f}}{{partial y}}frac{{dy}}{{dt}}normalsize.)
В другом случае:
(z = fleft( {xleft( {u,v} right),yleft( {u,v} right)} right))
В результате для определения частных производных целесообразно использовать следующие соотношения:
(largefrac{{partial z}}{{partial u}}normalsize = largefrac{{partial f}}{{partial x}}frac{{partial x}}{{partial u}}normalsize + largefrac{{partial f}}{{partial y}}frac{{partial y}}{{partial u}}normalsize,;;largefrac{{partial z}}{{partial v}}normalsize = largefrac{{partial f}}{{partial x}}frac{{partial x}}{{partial v}}normalsize + largefrac{{partial f}}{{partial y}}frac{{partial y}}{{partial v}}normalsize.)
Малые приращения функции находят по формуле:
(Delta z approx largefrac{{partial f}}{{partial x}}normalsizeDelta x + largefrac{{partial f}}{{partial y}}normalsizeDelta y)
Определение 8
Градиент функции u (x, y,…) представляет собой вектор с координатами в виде частных производных функции u по x, y,…
Градиент обозначают таким образом:
(grad u).
В том случае, когда u является функцией пары переменных:
(grad u = (u’x, u’y))
В том случае, когда u является функцией трех переменных:
(grad u = (u’_{x}, u’_{y}, u’_{z}))
Существует способ определения градиента для какой-то точки (M_{0}). Для этого требуется подставить координаты рассматриваемой точки в следующее выражение:
Представим, что функция (F(x, y, z)) возрастает, двигаясь от точки (M_{0}) к некой точке М. Таким образом, функция растет в соответствии с направлением вектора (overline{M_{0}М}). Существует характеристика для описания скорости этого роста.
Производная функции F в соответствии с направлением вектора overline{u}=overline{M_{0}М} представляет собой функцию:
Рассмотрим варианты поведения функции F в направлении вектора (overline{u}) на графике:
- функция является возрастающей, если (frac{dF}{du}>0);
- функция является убывающей, если (frac{dF}{du}<0);
- функция остается неизменной, если (frac{dF}{du}=0).
С целью определения производной (frac{dF}{du}) следует упростить вычисления и использовать при расчетах скалярное произведение:
Экстремум функции нескольких переменных
Функция (fleft( {x,y} right)) обладает неким локальным максимумом в точке с координатами (left( {{x_0},{y_0}} right)) в том случае, когда (fleft( {x,y} right) < fleft( {{x_0},{y_0}} right)) для всех (left( {x,y} right)), которые необходимо близки к (left( {{x_0},{y_0}} right)).
Функция (fleft( {x,y} right)) обладает неким локальным минимумом в точке с координатами (left( {{x_0},{y_0}} right)) в том случае, когда (fleft( {x,y} right) > fleft( {{x_0},{y_0}} right)) для всех (left( {x,y} right)), которые необходимо близки к (left( {{x_0},{y_0}} right)).
Точки экстремума функции являются точками максимума и минимума рассматриваемой функции.
Стационарные точки функции представляют собой такие точки, в которых каждая из частных производных для функции обладает нулевым значением.
Определить стационарные точки в случае функции пары переменных можно с помощью такой системы уравнений:
(largefrac{{partial f}}{{partial x}}normalsize = largefrac{{partial f}}{{partial y}}normalsize = 0).
Заметим, что по определению локальный максимум и локальный минимум являются стационарными точками функции. Данные точки совместно с точками, принадлежащими области определения функции, в которых отсутствуют частные производные функции, формируют некое множество критических точек этой функции.
Седловая точка является стационарной точкой, которую нельзя отнести ни к локальному максимуму, ни к локальному минимуму функции.
Предположим, что имеется некая точка (left( {{x_0},{y_0}} right)), в которой частные производные первого порядка принимают нулевые значения. Тогда заданная точка является стационарной точкой. Запишем выражение для определителя, в состав которого включены значения частных производных второго порядка, соответствующие данной точке:
(D = left| {begin{array}{*{20}{c}} {largefrac{{{partial ^2}f}}{{partial {x^2}}}normalsizeleft( {{x_0},{y_0}} right)} & {largefrac{{{partial ^2}f}}{{partial y,partial x}}normalsizeleft( {{x_0},{y_0}} right)}\ {largefrac{{{partial ^2}f}}{{partial x,partial y}}normalsizeleft( {{x_0},{y_0}} right)} & {largefrac{{{partial ^2}f}}{{partial {y^2}}}normalsizeleft( {{x_0},{y_0}} right)} end{array}} right|.)
Рассмотрим возможные варианты:
- Когда D > 0 и частная производная (largefrac{{{partial ^2}f}}{{partial {x^2}}}normalsizeleft( {{x_0},{y_0}} right) > 0), имеем, что (left( {{x_0},{y_0}} right)) определяется, как локальный минимум.
- При D > 0 и частной производной (largefrac{{{partial ^2}f}}{{partial {x^2}}}normalsizeleft( {{x_0},{y_0}} right) < 0) имеем, что (left( {{x_0},{y_0}} right)) определяется, как локальный максимум.
- Если D < 0, тогда (left( {{x_0},{y_0}} right)) представляет собой седловую точку.
- Если D обладает нулевым значением, то для идентификации вида стационарной точки требуется провести дополнительные исследования.
Уравнение касательной плоскости к поверхности (z = fleft( {x,y} right)) в некой точке с координатами (left( {{x_0},{y_0},{z_0}} right)) можно записать таким образом:
(z — {z_0} = largefrac{{partial f}}{{partial x}}normalsizeleft( {{x_0},{y_0}} right)left( {x — {x_0}} right) + largefrac{{partial f}}{{partial y}}normalsizeleft( {{x_0},{y_0}} right)left( {y — {y_0}} right).)
Уравнение нормали к поверхности (z = fleft( {x,y} right)) в некой точке с координатами (left( {{x_0},{y_0},{z_0}} right)) можно записать следующим образом:
(largefrac{{x — {x_0}}}{{frac{{partial f}}{{partial x}}left( {{x_0},{y_0}} right)}}normalsize = largefrac{{y — {y_0}}}{{frac{{partial f}}{{partial y}}left( {{x_0},{y_0}} right)}}normalsize = largefrac{{z — {z_0}}}{{ — 1}}normalsize.)
Как найти область определения функции многих переменных — подробная инструкция
При записи функции нескольких переменных (например, двух переменных) в виде формулы (z = f(x, y)), область определения этой функции является множеством всех значений точек плоскости ХОУ, при которых эта формула имеет смысл, и функция принимает действительные значения.
В действительности, принципы нахождения области определения функции нескольких переменных схожи с правилами для области определения функции одной переменной, которые соответствуют следующему алгоритму действий:
- определение типа или типов ограничений;
- запись и поиск корней соответствующих неравенств;
- запись интервала или интервалов допустимых значений аргумента.
Разница заключается в том, что в случае функции двух переменных область определения представляет собой какое-то множество точек плоскости, а не прямой, как для функции одной переменной.
Если рассматривается функция трех переменных, то областью определения станет множество точек, принадлежащих трехмерному пространству.
Когда речь идет о функции n переменных, область определения соответствует множеству точек абстрактного n-мерного пространства.
Область определения функции двух переменных с корнем n-й степени
Представим некую функцию:
(z=sqrt[n]{phi(x,y)})
Здесь n является каким-то натуральным числом. Запишем варианты для области определения функции при разных значениях n:
- При n в виде четного числа область определения функции соответствует множеству точек плоскости со всеми значениями подкоренного выражения, которые больше или равны нулю. Таким образом: (phi(x,y) geq 0).
- При n в виде нечетного числа область определения функции представляет собой множество каких-либо значений (phi(x,y)), то есть соответствует всей плоскости ХОУ.
Область определения степенной функции двух переменных, если показатель степени является целым числом
Когда функция имеет вид (z = (phi(x,y))^{a}), она определяется таким образом:
- при положительных значениях a область определения соответствует всей плоскости ХОУ, включая оси;
- при отрицательных значениях а область определения функции соответствует множеству значений (phi(x,y)), которые не равны нулю.
Область определения степенной функции двух переменных, если показатель степени является дробным числом
Когда функция имеет вид (z = (phi(x,y))^{ frac{a}{b}}), она определяется таким образом:
- при положительных значениях (frac{a}{b}) область определения соответствует множеству таких точек на плоскости, в которых (phi(x,y) geq 0);
- при отрицательных значениях (frac{a}{b}) область определения функции соответствует множеству точек на плоскости, в которых (phi(x,y)> 0).
Область определения логарифмической функции двух переменных
Рассмотрим логарифмическую функцию двух переменных, записанную в виде:
(z = log_{a}{phi(x,y)})
Данная функция определена в том случае, когда ее аргумент обладает положительным значением. Тогда областью определения функции является множество таких точек, в которых:
(phi(x,y)> 0.)
Область определения тригонометрических функций двух переменных
Рассмотрим варианты тригонометрических функций и их области определения:
- для функции (z = sin phi(x,y)) областью определения является полностью плоскость ХОУ;
- для функции (z = cos phi(x,y)) областью определения является полностью плоскость ХОУ;
- для функции (z = tg phi(x,y)) областью определения является полностью плоскость ХОУ, за исключением пар чисел, когда (phi(x,y)) обладает значениями (frac{pi}{2}+pi k,) где (kin Z);
- для функции (z =c tg phi(x,y)) областью определения является полностью плоскость ХОУ, за исключением пар чисел, когда (phi(x,y)) обладает значениями k, где (kin Z.)
Область определения обратных тригонометрических функций двух переменных
Рассмотрим варианты обратных тригонометрических функций и их области определения:
- для функции (z = arcsin phi(x,y)) областью определения является множество таких точек, при которых (-1leq phi(x,y) leq 1);
- для функции (z = arccos phi(x,y)) областью определения является множество таких точек, при которых (-1leq phi(x,y) leq 1);
- для функции (z = arctg phi(x,y)) областью определения является полностью плоскость ХОУ;
- для функции (z =arcc tg phi(x,y)) областью определения является полностью плоскость ХОУ.
Область определения дроби как функции двух переменных
Представим, что функция записана следующим образом:
(z = frac{a}{phi(x,y)})
В таком случае, область определения данной функции соответствует всем точкам плоскости при выполнении условия:
(phi(x,y) neq 0.)
Область определения линейной функции двух переменных
Предположим, что функция задана таким образом:
(z = ax + by + c)
В этом случае, область определения рассматриваемой функции соответствует полностью всей плоскости ХОУ.
Примеры решения задач
Задача 1
Дана функция, область определения которой требуется найти:
(z=frac{x^{2}+4xy-3}{x+y-5})
Решение
Заметим, что в данном случае не допускается нулевое значение для знаменателя. Поэтому:
(х + у — 5neq 0)
Тогда:
(уneq 5 – х)
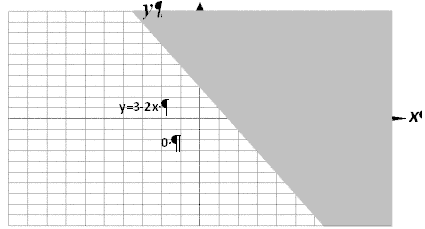
Ответ: областью определения данной функции является вся координатная плоскость ХОУ, за исключением точек, которые принадлежат прямой у= 5 – х.
Задача 2
Требуется найти область определения следующей функции:
(f(x;y) = sqrt{3y+2})
Решение
Заметим, что выражение, записанное под знаком корня, не может иметь отрицательное значение, поэтому:
(3у + 2 geq 0)
(3у geq -2)
(у geq -frac{2}{3})
Ответ: областью определения данной функции является полуплоскость у (geq -frac{2}{3})
Задача 3
Нужно найти область определения обратной тригонометрической функции двух переменных:
(z = arcsin frac{x}{y^{2}})
Решение
Руководствуясь стандартным алгоритмом для поиска области определения функции, запишем двойное неравенство:
(-1 leq frac{x}{y^{2}} leq 1)
Упростим выражение путем умножения обеих частей неравенства на (y^{2}:)
(- y^{2} leq х leq y^{2})
Ответ: область определения данной функции соответствует ( — y^{2} leq х leq y^{2}.)
Задача 4
Дана функция, область определения которой требуется найти:
(z = ln (y-x))
Решение
Руководствуясь стандартным алгоритмом для поиска области определения функции, запишем двойное неравенство:
(у – х > 0)
Выполним перенос переменной х вправо, получим:
(у>х)
Ответ: область определения данной функции соответствует (у>х.)
Задача 5
Дана следующая функция пары переменных:
S = xy
Нужно найти область определения данной функции, а также вычислить значение функции, если:
x = 3, y = 5.
Решение
Область определения функции S = xy, которая выражает связи между площадью многоугольника и длинами его сторон, можно представить в виде пары неравенств:
(х geq 0)
(у geq 0)
Данные выражения соответствуют первому квадранту на плоскости ХОУ.
Вычислим частное значение заданной функции при x = 3, y = 5:
(S_{0} = f(3, 5) = 3 cdot 5 = 15)
Ответ: первый квадрант плоскости ХОУ; 15.
Цели работы:
- повторить и систематизировать нахождение
области определения функции, закрепить это
понятие и наглядно представить в координатной
плоскости и в пространстве; - рассмотреть аналитические и геометрические
методы не изолированно друг от друга, а в тесной
взаимосвязи. Это позволит облегчить переход от
стандартных решений конкретных математических
задач к нестандартным; - воспитание интереса к математике и мультимедиа,
активности, мобильности; восприятие компьютера,
как инструмента обучения; - использование компьютера для нахождения
области определения и построения графиков с
помощью графического редактора 3D Grapher 1.2, Copyright ©
2000-2002 RomanLab Software и формирование информационной
компетентности учащихся.
Определение функции двух переменных
Если каждой паре ( x;y) значений двух
независимых друг от друга переменных величин х и
у из некоторого множества D соответствует
единственное значение величины, то говорят,
что z есть функция двух независимых
переменных x и y, определенная на
множестве D.
Обозначается: z=f(x;y) или z=z(x;y).
Например, 
S=ab, S=S(a;b)- функции двух переменных; V=abc,
V=V(a,b.c) – функция трех переменных;
A= 
–
функция трех переменных.
Способы задания функций нескольких
переменных
Чтобы задать функцию двух (трех) переменных,
нужно указать способ, с помощью которого для
каждой пары (тройки) значений аргументов можно
найти соответствующее значение функции.
Наиболее часто функция задается аналитически
— это
явное задание функции или неявное задание 
Например, 
— это явно заданная функция двух
переменных; уравнение 
задает неявно две функции двух
переменных
.
Область определения функции
Непрерывное множество пар 
значений независимых
переменных 
, при которых функция
определена,
называется областью определения функции.
Область определения называется замкнутой
областью, если она включает в себя свою границу;
открытой областью, если она не включает в себя
свою границу; ограниченной областью, если может
быть помещена в круг конечного радиуса.
Геометрически изобразить область определения
функции можно только для функций:
Геометрическое изображение самой функции
возможно только для функции двух переменных.
Графиком функции двух переменных является
поверхность, проектирующаяся на плоскость 
в область
D, которая является областью определения
функции.
На рис. изображена поверхность графика функции 
и ее область определения.
В курсе учебного материала 9-го класса мы
рассматриваем следующие задания на нахождение и
построение области определения функции.
ПРИМЕРЫ
Найти область определения функции 
Решение. Областью определения данной функции
является вся плоскость, т.к. нет ограничений на
переменные x и y.
2. Найти область определения функции 
.
Решение. Данная функция определена, когда xy
> 0, т.е. в тех точках координатной плоскости, в
которых знаки координат x и y —
одинаковы. Это будут точки, лежащие в I и III
координатных четвертях, т.е. множество точек,
удовлетворяющих условиям:
и 
3. Найти область определения функции 
.
Решение. Данная функция определена при
условии, когда
т.е. 
.
Это множество точек, лежащих внутри круга с
центром в начале координат, радиус которого
равен 2.
Изобразить на координатной плоскости Оху
область определения функции 
.
Решение. Подкоренное выражение должно быть
неотрицательно, т.е. 
следовательно, 
. Геометрическим
решением неравенства служит полуплоскость,
расположенная выше прямой 
и сама прямая.
5. Найти область определения функции и
изобразить её графически.
.
Решение. Областью определения функции является
множество точек плоскости, координаты которых
удовлетворяют системе неравенств:
6. Изобразить на координатной плоскости
Оху область определения функции
Решение. Эта функция определена, когда
подкоренное выражение неотрицательно, т.е. 
Данным
соотношениям удовлетворяют координаты всех
точек, находящихся внутри кольца, образованного
двумя окружностями с центрами в начале координат
и радиусами R=3, R=4.
7. Изобразить на координатной плоскости Оху
область определения функции
.
Решение. Учащиеся не могут найти область
определения данной функции аналитически, но с
помощью графического редактора 3D Grapher 1.2 это
выполняется легко.
В Приложении приведено ещё несколько примеров,
с решениями, для учащихся девятых классов.
Для учащихся 10-11 классов мы предлагаем систему
упражнений по нахождению и построению области
определения функции двух переменных. При этом
отрабатываются свойства логарифмических,
тригонометрических и обратных
тригонометрических функций. Данные упражнения
можно использовать при изучении нового
материала, при повторении, при решении уравнений
и неравенств.
Найти и изобразить на плоскости область
определения функции
Решение. Область определения функции есть
пересечение областей определения слагаемых
функции. Для первой функции подкоренное
выражение должно быть неотрицательным, т.е. 
Если
значение логарифмической функции
неотрицательно, то выражение, стоящее под знаком
логарифма, должно быть больше или равно единице,
т.е. 
отсюда 
.
Это неравенство задает нам множество точек
плоскости, лежащих вне окружности с центром в
начале координат, радиуса 2, включая и точки
данной окружности. Вторая функция 
определена при 
Следовательно, 
Имеем две параболы с вершиной в начале
координат 
. Поэтому полученное неравенство
задает нам часть плоскости, заключенную между
этими параболами, включая границы без начала
координат. Третья функция определена при 
Областью определения данной функции является
общая часть найденных областей определения
слагаемых.
Покажите на координатной плоскости xOy область
определения функции
.
Решение. Ограничения для функции имеют вид: 
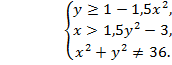
3. Изобразить область определения функции
Решение. Эта функция определена при 
, т.е.
Областью определения является часть плоскости,
расположенная между двумя прямыми.
4. Найти область определения функции 
.
Решение. Областью определения функции 
является
решение неравенства
. Поэтому нужно решить
неравенство 
Решая данное неравенство, получим 
Это область,
заключенная между двумя параболами 
и 
.
5. Построить область определения функции 
Решение. Область определения данной функции
определяется системой неравенств:
Первое неравенство определяет круг с центром в
точке (-2;0) и радиусом равным 2 за исключением его
границы: 
Второе неравенство определяет I и III
координатные четверти, за исключением осей.
В Приложении приведено ещё несколько примеров,
с решениями, для учащихся десятых и одиннадцатых
классов.
Рассмотрим задание С5, используя функцию двух
переменных.
Найдите все значения параметра а, при
которых система
, имеет ровно два решения.
Решение. Из второго уравнения находим y =
. Первое
уравнение принимает вид 
.
Пусть 
.
В этом случае уравнение имеет единственное
решение 
.
Запишем второе уравнение в виде 
= 0. Его дискриминант равен
4 
, и он
положителен, поскольку . Уравнение имеет два различных
корня 
и 
Значит,
в этом случае система имеет ровно два решения 
и 
.
Пусть теперь 
1. В этом случае уравнение 
если и имеет корни,
то только больше единицы
Но тогда дискриминант
уравнения = 0
отрицателен. Решений нет.
Ответ: .
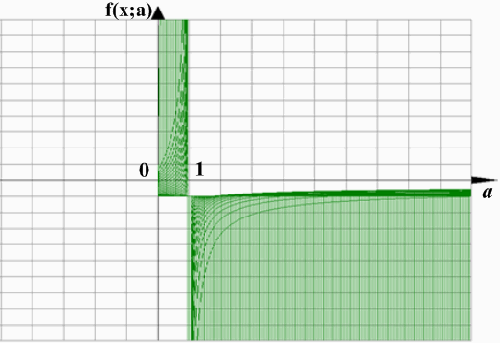
С помощью графического редактора задаем
функцию двух переменных 
, 
Находим значения а, при которых
функция обращается в ноль.
На рисунке видно, что решением является
интервал от 0 до 1.
При подготовке учащихся к итоговой аттестации
мы сталкиваемся с тем, что задания уровня С5
решаются тяжело и не сразу. А ведь это функция
двух переменных! Оперирование геометрическими
образами упрощает решение задач с параметрами, а
в некоторых случаях геометрический подход часто
является единственно возможным методом решения.
В сборнике ЕГЭ-2011 предложено задание.
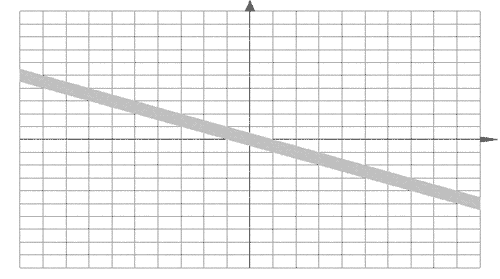
Найдите все значения а, такие, что для любого х
выполняется неравенство
.
Решение. Рассмотрим функцию 
Если
то
убывает.
Если 
то 
возрастает.
Значит, наименьшее значение функции 
равно или
, или 
. Поэтому
решение задачи получаем из решения системы
Решений нет.
Ответ: 
.
C помощью графического редактора мы построили
график функции и определили значение параметра а
при 
.
График функции в системе координат выглядит
следующим образом.
Приложение 1
Приложение 2
Приложение 3
Список источников и литературы.
- Математика (математический анализ):
учебно-методическое пособие для студентов
нематематических специальностей / О.Ю. Ватюкова,
Е.Е.Зайцева, Ю.В.Зайцева и др.; ВолГУ.-4-е изд.,
Волгоград: Волгоградское научное издательство,
2009. – 238с. - Дифференциальное исчисление функций
нескольких переменных: типовой расчет по высшей
математике / Сост.: А. В. Анкилов, Н. Я. Горячева, Т.
Б. Распутько.- Ульяновск: УлГТУ, 2004.-32 с. - ЕГЭ 2011. Математика. Типовые тестовые задания /
И.Р. Высоцкий, Д.Д. Гущин, П.И.Захаров, В.С. Панферов,
и др.; под ред. А.Л. Семенова, И.В. Ященко. -М.:
Издательство “Экзамен”, 2011.-63с. - Самое полное издание типовых вариантов
реальных заданий ЕГЭ: 2010: Математика/авт.- сост.
И.Р.Высоцкий, Д.Д. Гущин, П.И. Захаров и др.; под ред.
А.Л. Семенова, И.В. Ященко. -М.: АСТ: Астрель, 2010.-93с. - Мордкович А.Г. Алгебра . 9 класс. В 2 ч. Ч.1. Учебник
для учащихся общеобразовательных учреждений /
А.Г.Мордкович, П.В.Семенов .—11-е изд., стер. -М.:
Мнемозина, 2009.-224 с. - Смирнова И.М. Геометрия. 10-11 кл.: Учеб. для
общеобразоват. учреждений (гуманитарный
профиль).- М.: Мнемозина,2004. -223с.
Примеры решений задач: функции нескольких переменных
В этом разделе вы найдете готовые задания разного типа для функций нескольких переменных:
Спасибо за ваши закладки и рекомендации
Примеры: область определения ФНП
Задача 1. Найти область определения функции двух переменных $z=f(x,y)$. Изобразить ее на координатной плоскости и заштриховать.
$$z=frac{4+x}{(x+3)(y-5)}.$$
Задача 2. Для данной функции найти область определения и изобразить ее на рисунке в системе координат.
$$z=frac{sqrt{xy}}{x^2+y^2}.$$
Примеры: частные производные ФНП
Задача 3. Найти частные производные: $z=tg^3 (3x-4y)$
Задача 4. Найти частные производные второго порядка $z=sqrt{x^2-y^2}$
Задача 5. Найти частные производные сложной функции:
$$ z=u^2 cdot ln v; quad u=frac{x}{y}, , v=x^2+y^2.$$
Задача 6. Проверить справедливость теоремы о смешанных производных второго порядка.
$$z=ln (x^2+y^2).$$
Задача 7. Найти полный дифференциал данной функции
$$z=arctg (y-x) +frac{1}{sqrt{y}} +sqrt[3]{y}cdot ln (1-x) +sin 2x+1.$$
Задача 8. Найти дифференциал второго порядка функции:
$$z= arctgfrac{x}{x+y}$$
Задача 9. Для функции $z(x,y)$ двух переменных, неявно заданной уравнением $sin(xz)+cos(yz)=1$, найдите первый и второй дифференциалы в точке $x=y=1, z=0$.
Задача 10. Проверить, удовлетворяет ли функция двух переменных $z(x,y)$ указанному дифференциальному уравнению.
$$
z=xsin frac{y}{x}+ylnfrac{y}{x},\
y frac{partial^2 z}{partial y^2}+xfrac{partial^2 z}{partial xpartial y}=0.
$$
См. также: примеры на производные, ДУ в частных производных
Градиент, производная по направлению
Задача 11. Найти производную функции $f(x,y,z)$ в точке $M(x_0,y_0,z_0)$ по направлению вектора $overline{l}$. Вычислить наибольшую скорость изменения функции в данной точке.
$$
f=sin (x+2y)+sqrt{xyz}, quad overline{l}={4,3,0}, , M_0(pi/2; 3pi /2;3).
$$
Задача 12.Дана функция $z(x,y)$, точка $A(x_0,y_0)$ и вектор $overline{a}$. Найти:
1) $grad z$ в точке $A$;
2) производную в точке $A$ по направлению вектора $overline{a}$.
$$z=arctg(xy^2), quad A(2;3), , overline{a}=4overline{i}-3overline{j}. $$
Задача 13. Найдите градиент, производную по направлению $overline{l}$ и матрицу Гессе в точке $M$ заданной функции, где $u=f(x,y,z)=x^2z+z^2x^2+y^3$, $overline{l}={2;1;-2}$, $M(1,3,1)$.
Задача 14. Найти производную функции $u$ в точке $M$ по направлению нормали к поверхности $S$, образующей острый угол с положительным направлением оси $Oz$.
$$
u=(x^2+y^2+z^2)^{3/2}, S: 2x^2-y^2+z^2-1=0, M=(0,-3,4).
$$
Касательная плоскость и нормаль
Задача 15. Составить уравнения касательной плоскости и нормали к поверхности $x^2+y^2-x+2y+4z-13=0$
в точке $M(2,1,2)$.
Задача 16. Для кривой $overline{r}=overline{r}(t)$ найти в точке $t_0$ уравнение касательной, уравнение нормальной плоскости и вычислить кривизну линии.
$$ overline{r}(t)=(t^2-3)overline{i} + (t^3+2)overline{j}+ln t overline{k}, quad t_0=1 $$
Задача 17. Найти градиент, первый дифференциал, матрицу вторых производных, второй дифференциал функции $z=2xy-xy^4+5y^3-3$ в точке $A(2,-3)$. Составить уравнения касательной плоскости и соприкасающегося параболоида к графику данной функции.
Экстремумы функции нескольких переменных
Задача 18. Найти точки экстремума функции $z=x^2+xy+y^2+2x-y$.
Задача 19. Найти точки локального экстремума и экстремальные значения $z=x^2+y^2-xy+x+y$.
Задача 20. Исследовать на экстремум функцию $z=x^4+xy+frac{1}{2}y^2+5$.
Задача 21. Определите, при каких значениях параметра $a$ функция $z(x,y)=x^3+y^3+4xy-7x-7y+a(x-1)^2+a(y-1)^2$ в точке (1;1):
А) имеет максимум,
Б) имеет минимум,
В) не имеет экстремума.
Задача 22. Найдите (локальные) экстремумы функции трех переменных $f(x,y,z)=2x^2-xy+2xz-y+y^3+z^2$.
Приближенные вычисления
Задача 23. Вычислить приближенно значение функции $Z=Z(x,y)$ и данной точке с помощью дифференциала.
$$ z=x+y-sqrt{x^2+y^2}, quad M(2,9;3,8)$$
Задача 24. Дана функция $z=x^2+2xy+3y^2$ и две точки $А (2; 1)$ и $В (1,96; 1,04)$. Требуется:
1) вычислить точное значение функции в точке $В$;
2) вычислить приближённое значение функции в точке $В$, исходя из значения функции в точке $А$ и заменив приращение функции при переходе от точки $А$ к точке $B$ дифференциалом;
3) оценить в процентах относительную погрешность, получающуюся при замене приращения функции её дифференциалом.
Ряд Тэйлора
Задача 25. Разложите функцию $f(x,y)=x^2ln y + y^2$ по формуле Тейлора (с остаточным членом в форме Пеано) в окрестности точки $M(2;1)$ до членов второго порядка включительно. Выпишите первый и второй дифференциалы заданной функции.
Задача 26. Найти первые и вторые частные производные функции $F$ и записать формулу Тэйлора в указанной точке $x^0$.
$$ F=ln(2x+y+z)+sin(2x+y+z)+x^22^{-2y}, quad x^0=(1,1,0). $$
См. также: примеры на ряды
Наибольшее и наименьшее значение в области
Задача 27. Найти наименьшее $m$ и наибольшее $M$ значения функции $z=f(x,y)=3-2x^2-xy-y^2$ в замкнутой области $D$, заданной системой неравенств $-1 le x le 1; 0le y le 2$. Сделать чертёж области $D$.
Задача 28. Экстремумы функций нескольких переменных. Требуется найти наибольшее и наименьшее значения функции $z=5x^2-3xy+y^2+4$ в области, ограниченной заданными линиями $x=0, y=0, x+y=2$.
Решение контрольной
Контрольное задание. Дана функция $f(x,y)=x^2+y^2-3xy$
1. Исследовать функцию $f$ на экстремум. Найти экстремальные значения функции.
2. Найти наибольшее и наименьшее значения функции $f$ в заданной области $D$.
3. Составить уравнение касательной плоскости к поверхности $z=f(x,y)$ в точке, где $x=x_0=1$, $y=y)0=3$.
4. Найти величину наибольшей скорости возрастания функции $f$ в точке $M_1(-1;1)$.
5. Вычислить производную функции $f$ в точке $M_1$ в направлении вектора $overline{M_1M_2}$. Каков характер изменения функции? Почему?
6. Найти угол между градиентами функции $f$ в точках $M_1$ и $M_2(2;2)$. Построить векторы и указать угол.
Помощь с решением заданий
Если вам нужна помощь с решением задач и контрольных по этой и другим темам математического анализа, обращайтесь в МатБюро. Стоимость подробной консультации от 100 рублей, оформление производится в Word, срок от 1 дня.
Проконсультируем по задачам ФНП с результатом!
Полезные ссылки
- Учебник с примерами онлайн по функциям нескольких переменных
- Теория поля — задачи с решениями
Функции нескольких переменных
ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
Пусть: z — переменная величина с областью изменения R; R- числовая прямая; D — область на координатной плоскости R2.
Любое отображение D->R называют функцией двух переменных с областью определения D и пишут z = f(x;y).
Если каждой паре (х; у) двух независимых переменных из области D по некоторому правилу ставится в соответствие одно определенное значение z из R, то переменную величину z называют функцией двух независимых переменных х и у с областью определения D и пишут
Аналогичным образом определяются функции многих переменных
П р и м е р 1. Найти и изобразить область определения функции
Область определения – есть плоскость хОу за исключением точек, лежащих на параболе у = х2, см. рисунок.
П р и м е р 2. Найти и изобразить область определения функции
Область определения – есть часть плоскости, лежащая внутри круга радиуса г = 3 , с центром в начале координат, см. рисунок.
П р и м е р 3. Найти и изобразить область определения функции
Область определения – есть часть плоскости, в которой абсцисса и ордината каждой точки имеют одинаковые знаки, т. е. это часть плоскости, лежащая в первом и третьем координатных углах, см. рисунок.
К числу функций нескольких переменных относятся производственные функции.
Производственными функциями называют функции, представляющие зависимости величин объемов выпускаемой продукции от переменных величин затрат ресурсов.
Производственные функции применяются не только в микроэкономических, но и в макроэкономических расчетах.
Простейшая производственная функция — функция зависимости объема произведенной работы V от объемов трудовых ресурсов R и вложенного в производство капитала К
2.ГЕОМЕТРИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ ФУНКЦИИ ДВУХ
2.1.График функции двух переменных
Рассмотрим в пространстве прямоугольную систему координат и область D на плоскости хОу. В каждой точке М(х;у) из этой области восстановим перпендикуляр к плоскости хОу и отложим на нем значение z = f(x; у). Геометрическое место полученных точек
является пространственным графиком, функции двух переменных.
Это некоторая поверхность.
Равенство z = f(x; у) называется уравнением этой поверхности.
Функция двух переменных имеет наглядную геометрическую интерпретацию. Для функции числа переменных n > 2 аналогом поверхности является гиперповерхность (n + 1) — мерного пространства, не имеющая геометрической интерпретации.
Линией уровня функции двух переменных z = f(x; у) называется линия f(x; у) = С (С = const) на плоскости хОу, в каждой точке которой функция сохраняет постоянное значение С.
Линия уровня представляет собой сечение поверхности графика функции двух переменных z = f(x; у) плоскостью z = С.
Поверхностью уровня функции трех переменных
u = f(x; у; z) называется поверхность в R3 (трехмерном пространстве), в каждой точке которой функция сохраняет постоянное значение f(x;y;z) = C (С = const).
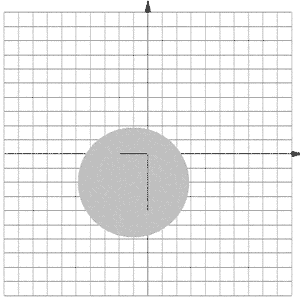
П р и м е р. Найти и построить линии уровня функции
Решение.
Линии уровня z = С данной функции имеют уравнения
Это окружности с центром в начале координат, радиусом R = C1/2 и уравнением
x2 + y2 = R2, см. рисунок.
Линии уровня позволяют представить рассматриваемую поверхность, дающую в сечении плоскостями z = C концентрические окружности.
При построении графика функции часто пользуются методом сечений.
П р и м е р. Построить график функции 
и найти 
.
Решение. Воспользуемся методом сечений.
– в плоскости 
– парабола.
– в плоскости 
–парабола.
– в плоскости 
– окружность.
Искомая поверхность – параболоид вращения.
Расстоянием между двумя произвольными точками 
и 
(евклидова) пространства 
называется число
Множество точек 
называется открытым кругом радиуса с центром в точке r.
Открытый круг радиуса ε с центром в точке A называется — ε — окрестностью точки А.
Найти и изобразить графически область определения функции:
Построить линии уровня функций:
3. ПРЕДЕЛ ФУНКЦИИ ДВУХ ПЕРЕМЕННЫХ
Основные понятия математического анализа, введенные для функции одной переменной, распространяются и на функции нескольких переменных.
О п р е д е л е н и е:
Постоянное число А называется пределом функции двух переменных z = f(x;у) при х —> х0, у —> у0, если для любого
ε >0 существует δ >0 такое, что |f(х; у) — А| 0 — постоянное число.
Постоянное число А называется пределом функции двух переменных f(x;y) = f(M) при стремлении точки М к точке М0, если для любого ε >0 можно найти такое число г >0, что как только расстояние |М0М| 0.
Предел отношения 
при Δs—>0 называется произ-
водной функции z = f(х; у) в точке (х; у) по направлению вектора 
и обозначается
Переходя к этому пределу, получим
(*)
Таким образом, зная частные производные функции
z = f(x; у) можно найти производную этой функции по любому направлению, а каждая частная производная является частным случаем производной по направлению.
П р и м е р. Найти производную функции
в точке М(1;0) в направлении, составляющем с Ох угол в 30°.
Следовательно, функция z = f(x;y) в данном направлении возрастает.
Градиентом функции z = f(x; у) называется вектор 
, координатами которого являются соответствующие частные производные данной функции
Связь между производной функции по направлению и градиентом этой функции осуществляется соотношением
т. е. производная функции z = f(x;y) в данном направлении равна проекции градиента функции на направление дифференцирования.
Градиент функции в каждой точке направлен по нормали к соответствующей линии уровня данной функции.
Направление градиента функции в данной точке есть направление наибольшей скорости возрастания функции в этой точке.
Примеры решений задач: функции нескольких переменных
В этом разделе вы найдете готовые задания разного типа для функций нескольких переменных:
Примеры: область определения ФНП
Задача 1. Найти область определения функции двух переменных $z=f(x,y)$. Изобразить ее на координатной плоскости и заштриховать.
Задача 2. Для данной функции найти область определения и изобразить ее на рисунке в системе координат.
Примеры: частные производные ФНП
Задача 3. Найти частные производные: $z=tg^3 (3x-4y)$
Задача 4. Найти частные производные второго порядка $z=sqrt$
Задача 5. Найти частные производные сложной функции:
$$ z=u^2 cdot ln v; quad u=frac, , v=x^2+y^2.$$
Задача 6. Проверить справедливость теоремы о смешанных производных второго порядка.
Задача 7. Найти полный дифференциал данной функции
Задача 8. Найти дифференциал второго порядка функции:
Задача 9. Для функции $z(x,y)$ двух переменных, неявно заданной уравнением $sin(xz)+cos(yz)=1$, найдите первый и второй дифференциалы в точке $x=y=1, z=0$.
Задача 10. Проверить, удовлетворяет ли функция двух переменных $z(x,y)$ указанному дифференциальному уравнению.
Градиент, производная по направлению
Задача 11. Найти производную функции $f(x,y,z)$ в точке $M(x_0,y_0,z_0)$ по направлению вектора $overline$. Вычислить наибольшую скорость изменения функции в данной точке.
Задача 13. Найдите градиент, производную по направлению $overline$ и матрицу Гессе в точке $M$ заданной функции, где $u=f(x,y,z)=x^2z+z^2x^2+y^3$, $overline=<2;1;-2>$, $M(1,3,1)$.
Задача 14. Найти производную функции $u$ в точке $M$ по направлению нормали к поверхности $S$, образующей острый угол с положительным направлением оси $Oz$.
Касательная плоскость и нормаль
Задача 15. Составить уравнения касательной плоскости и нормали к поверхности $x^2+y^2-x+2y+4z-13=0$ в точке $M(2,1,2)$.
Задача 16. Для кривой $overline=overline(t)$ найти в точке $t_0$ уравнение касательной, уравнение нормальной плоскости и вычислить кривизну линии.
$$ overline(t)=(t^2-3)overline + (t^3+2)overline+ln t overline, quad t_0=1 $$
Задача 17. Найти градиент, первый дифференциал, матрицу вторых производных, второй дифференциал функции $z=2xy-xy^4+5y^3-3$ в точке $A(2,-3)$. Составить уравнения касательной плоскости и соприкасающегося параболоида к графику данной функции.
Экстремумы функции нескольких переменных
Задача 18. Найти точки экстремума функции $z=x^2+xy+y^2+2x-y$.
Задача 19. Найти точки локального экстремума и экстремальные значения $z=x^2+y^2-xy+x+y$.
Задача 20. Исследовать на экстремум функцию $z=x^4+xy+frac<1><2>y^2+5$.
Задача 21. Определите, при каких значениях параметра $a$ функция $z(x,y)=x^3+y^3+4xy-7x-7y+a(x-1)^2+a(y-1)^2$ в точке (1;1):
А) имеет максимум,
Б) имеет минимум,
В) не имеет экстремума.
Задача 22. Найдите (локальные) экстремумы функции трех переменных $f(x,y,z)=2x^2-xy+2xz-y+y^3+z^2$.
Приближенные вычисления
Задача 23. Вычислить приближенно значение функции $Z=Z(x,y)$ и данной точке с помощью дифференциала.
Задача 24. Дана функция $z=x^2+2xy+3y^2$ и две точки $А (2; 1)$ и $В (1,96; 1,04)$. Требуется:
1) вычислить точное значение функции в точке $В$;
2) вычислить приближённое значение функции в точке $В$, исходя из значения функции в точке $А$ и заменив приращение функции при переходе от точки $А$ к точке $B$ дифференциалом;
3) оценить в процентах относительную погрешность, получающуюся при замене приращения функции её дифференциалом.
Ряд Тэйлора
Задача 25. Разложите функцию $f(x,y)=x^2ln y + y^2$ по формуле Тейлора (с остаточным членом в форме Пеано) в окрестности точки $M(2;1)$ до членов второго порядка включительно. Выпишите первый и второй дифференциалы заданной функции.
Задача 26. Найти первые и вторые частные производные функции $F$ и записать формулу Тэйлора в указанной точке $x^0$.
Наибольшее и наименьшее значение в области
Задача 27. Найти наименьшее $m$ и наибольшее $M$ значения функции $z=f(x,y)=3-2x^2-xy-y^2$ в замкнутой области $D$, заданной системой неравенств $-1 le x le 1; 0le y le 2$. Сделать чертёж области $D$.
Задача 28. Экстремумы функций нескольких переменных. Требуется найти наибольшее и наименьшее значения функции $z=5x^2-3xy+y^2+4$ в области, ограниченной заданными линиями $x=0, y=0, x+y=2$.
Решение контрольной
Контрольное задание. Дана функция $f(x,y)=x^2+y^2-3xy$
1. Исследовать функцию $f$ на экстремум. Найти экстремальные значения функции.
2. Найти наибольшее и наименьшее значения функции $f$ в заданной области $D$.
3. Составить уравнение касательной плоскости к поверхности $z=f(x,y)$ в точке, где $x=x_0=1$, $y=y)0=3$.
4. Найти величину наибольшей скорости возрастания функции $f$ в точке $M_1(-1;1)$.
5. Вычислить производную функции $f$ в точке $M_1$ в направлении вектора $overline$. Каков характер изменения функции? Почему?
6. Найти угол между градиентами функции $f$ в точках $M_1$ и $M_2(2;2)$. Построить векторы и указать угол.
Помощь с решением заданий
Если вам нужна помощь с решением задач и контрольных по этой и другим темам математического анализа, обращайтесь в МатБюро. Стоимость подробной консультации от 100 рублей , оформление производится в Word, срок от 1 дня.
Функции многих переменных примеры с решением
Содержание:
Основные понятия о функциях многих переменных
Изучение связей и закономерностей, существующих в материальном мире, часто приводят к функции не одной, а многих переменных. Эти функции позволяют выражать более сложные зависимости, чем функции одной переменной. Поэтому теория функций многих переменных имеет широкое практическое применение в различных отраслях.
Определение функции многих переменных. Функция двух переменных и ее графическое изображение
Переменные x1, x2, . xn называются независимыми между собой, если каждая из них может принимать произвольные значения в своей области изменения независимо от того, какие значения принимают при этом другие переменные.
Определение 1. Функцией многих переменных u = f (x1, x2, . xn) называется такая закономерность, при которой переменным x1, x2, . xn из некоторого множества D ⊂ R n ставится в соответствие одно значение u из множества E ⊂ R’.
Например: 
Множество D называется областью определения функции u = f (x1, x2, . xn), а множество E — областью значений этой функции. Например, функция 
задана для всех x и y, для которых выполняется неравенство x 2 + y 2 ≤ 9. В данном случае областью определения функции является круг на плоскости Оxy с центром в точке O (0; 0) и радиусом R = 3. Область значений этой функции E = [0; 3].
Частным случаем функции многих переменных есть функция двух переменных z = f (x, y), для которой можно дать понятие графика функции. В общем случае графиком такой функции является поверхность в трехмерном пространстве R 3 .
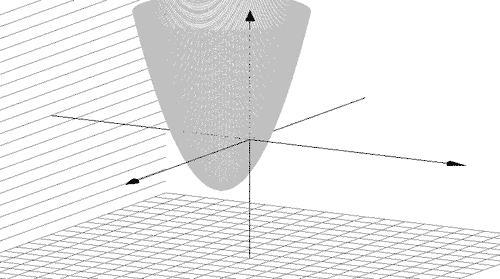
Пример 1. z = x 2 + y 2 . Графиком этой функции является параболоид вращения (рис. 1).
Экономические задачи, приводящие к понятию функций многих переменных
Приведем примеры конкретных функций многих переменных, которые встречаются в экономических задачах.
Пример 2. Пусть предприятие выпускает только один товар, и на его выпуск затрачивается только одно сырье (один ресурс). Предприятие характеризуется полностью своей производственной функцией y = f (x) — зависимость объема выпущенного товара y от объема затраченного сырья x. Такая производственная функция называется одноресурсной.
Если на производство продукции определенного типа расходуются многие виды сырья (ресурсов) x1, x2, . xn , то такая производственная функция называется многоресурсной или многофакторной:
y= F (x) = F (x1, x2, . xn).
Наиболее известной производственной функцией является функция Кобба-Дугласа y = AK α L β , где A, α, β — неотрицательные константы, причем α + β ≤ 1;
K — объем фондов в стоимостном или натуральном выражении;
L — объем трудовых ресурсов — число работников, число человеко-дней;
y — выпуск продукции в стоимостном или натуральном выражении.
На этом примере видно, что функция Кобба-Дугласа является функцией двух независимых переменных K и L.
Пример 3. Рассмотрим основное уравнение классической количественной теории денег, которое называется уравнением обмена Фишера: MV = PY.
В данном уравнении любая из переменных M, V, P, Y может рассматриваться как функция трех переменных, где
M — это общее количество денег, имеющихся в обороте;
V — скорость их оборота (сколько раз каждый рубль участвует в расчетах в среднем за год);
Y — национальный продукт или доход (национальный продукт — это все готовые товары и услуги, произведенные в экономической системе в стоимостном выражении; национальный доход — это все выплаты, полученные домашними хозяйствами: заработная плата, рента, прибыль; национальный продукт и национальный доход численно равны);
P — уровень цен (среднее взвешенное значение цен готовых товаров и услуг, которые определены относительно базового показателя, принятого за единицу).
Пусть 
, то есть цена является функцией трех независимых переменных. Тогда с увеличением денежной массы (количества денег) M в несколько раз (то есть деньги просто напечатают), цены вырастут во столько же раз, при условии, что другие величины V и Y останутся неизменными. Такие действия и является чаще всего причиной инфляции.
Функции многих переменных. Понятие функции многих переменных
Ранее рассматривались числовые функции 
одной переменной 
. Областью определения такой функции являлось множество 
. Числовая функция 
переменных характеризуется тем, что областью ее определения является подмножество 
пространства 
. В этом случае значение аргумента 
представляет собой точку 
.
Определение 1. Пусть имеются два множества 
и 
, и указано правило 
, по которому каждому элементу 
ставится в соответствие единственный элемент 
. Тогда говорят, что задана функция 
переменных 
из 
в 
:
. (1)
Как и ранее, 
— область определения функции , 
— область значений функции .
Для функций двух переменных ( 
= 2) вместо 
пишут обычно 
и тогда (1)принимает вид
. (2)
Функция двух переменных геометрически определяет некоторую поверхность в 
. Ее область определения состоит из точек 
расположенных на плоскости 
. Каждой из этих точек соответствует единственная число 
, которое является аппликатой точки 
данной поверхности. Поэтому говорят, что 
есть функция точки 
, и пишут 
. Эту аналогию можно распространить на случай 
> 2. Тогда область определения будет состоять из точек 
, а функция (1.19) будет записана в виде 
.
Поверхность 
— это сфера радиуса 
с центром в точке (0,0,0). Она не является функцией двух переменных, так как точке 
соответствуют два числа 
. Однако функцией будет, например, верхняя часть сферы 
(рис. 1, а).
Другим примером функции двух переменных может служить эллиптический параболоид 
(рис. 1, б). Если эту поверхность пересечь плоскостью, параллельной плоскости 
, то линией пересечения будет эллипс. Если же плоскость пересечения параллельна 
или 
, то линией пересечения будет парабола.
Уравнением 
задается гиперболический параболоид. График этой функции двух переменных имеет форму седла (рис. 1, в). Если эту поверхность пересечь плоскостью, параллельной плоскости , то линией пересечения будет гипербола. Если же плоскость пересечения параллельна или , то линией пересечения будет парабола.
Еще одним примером функции многих переменных может служить производственная функция Кобба-Дугласа. Ее классический вид
(3)
где 
— объем выпуска продукции; где 
— затраты труда; где 
— затраты производственных фондов (рис. 2). Константы 
и 
— положительны, как и переменные , , . Сумма параметров , и 1-, равна единице. Это означает, что при увеличении производственных ресурсов и на одну единицу объем продукции также увеличивается на единицу. Следовательно, темпы роста перечисленных показателей совпадают.
Исследования показали, что зависимость (3) редко встречается на практике. Поэтому справедлив более общий вид производственной функции Кобба-Дугласа:
(4)
где 
— положительная константа. В отличие от предыдущего случая сумма параметров 
может быть как больше, так и меньше единицы. Если 
> 1, то темпы роста объема выпуска продукции выше, чем темпы роста производственных ресурсов и . Если же
Присылайте задания в любое время дня и ночи в ➔ 
Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.
Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.
Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.
http://www.matburo.ru/ex_ma.php?p1=mafnp
http://natalibrilenova.ru/funktsii-mnogih-peremennyih-primeryi-s-resheniem/