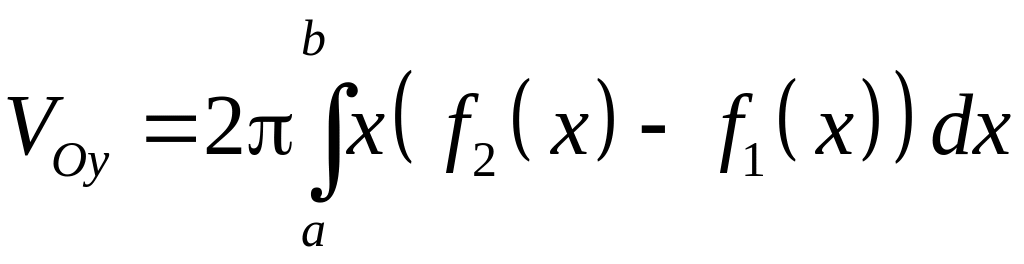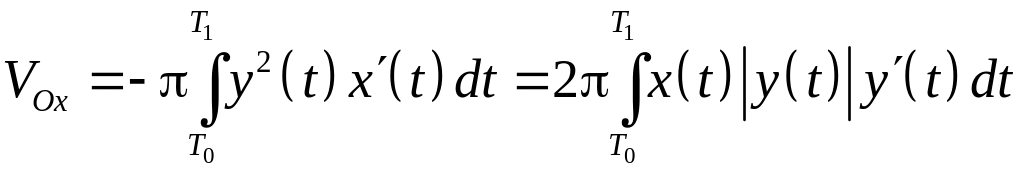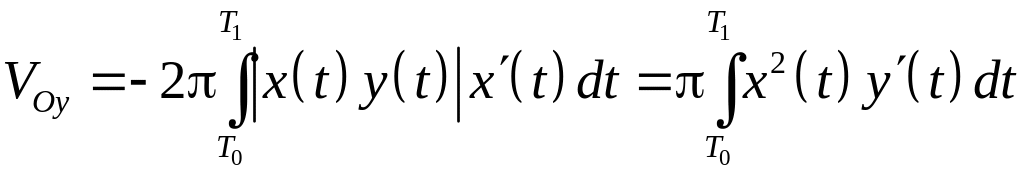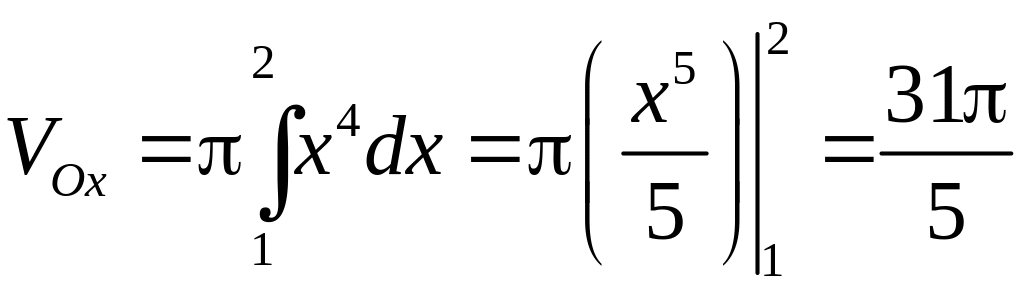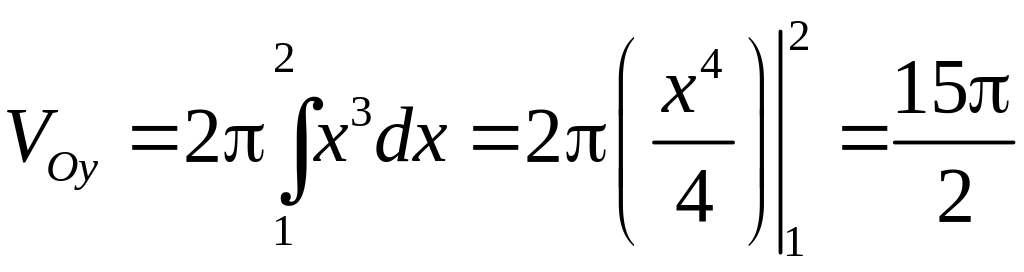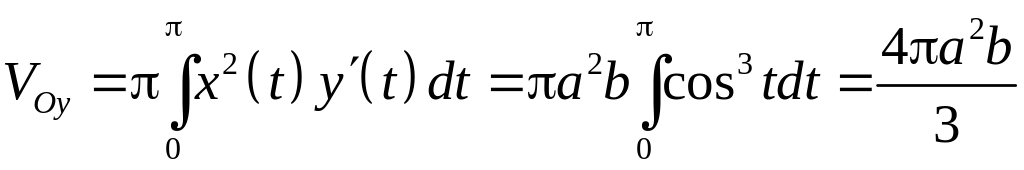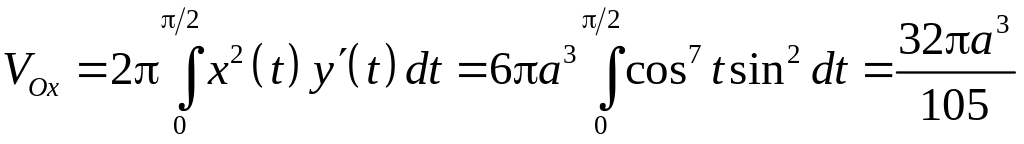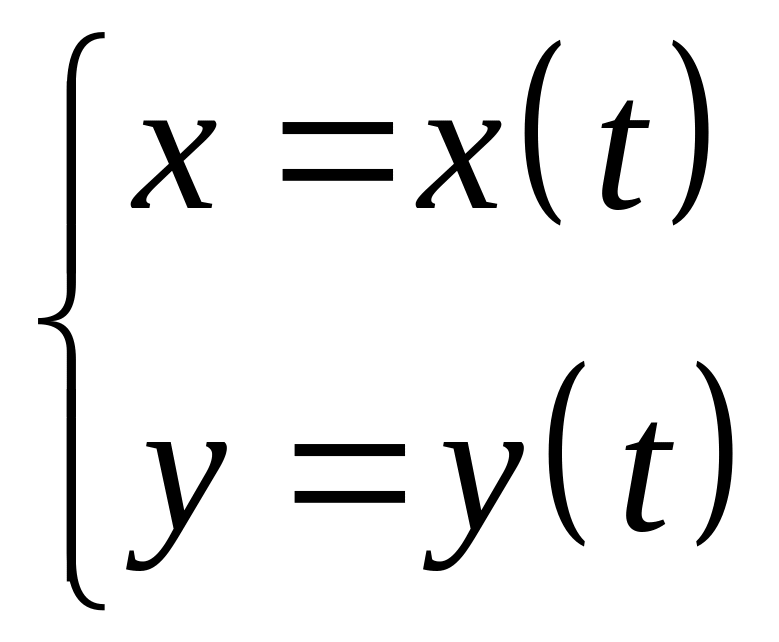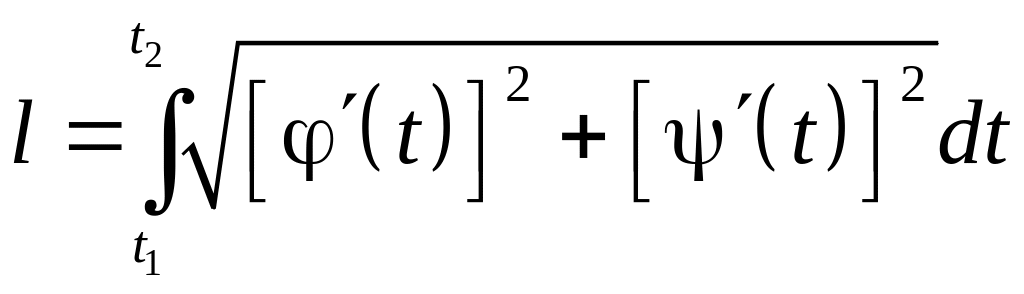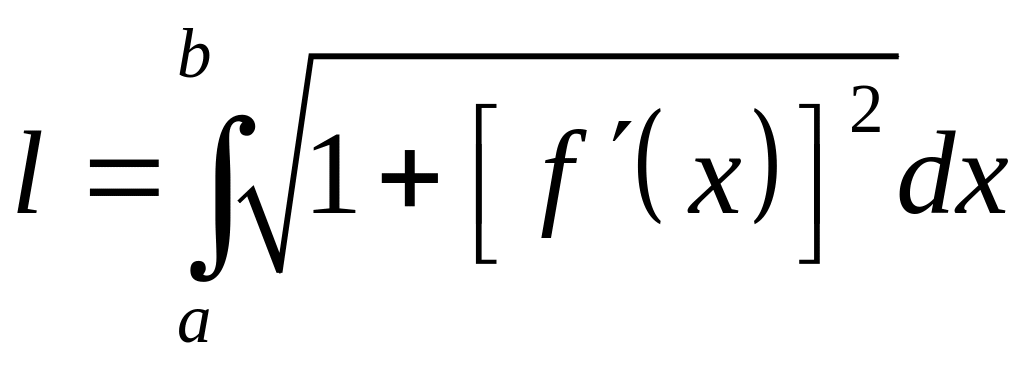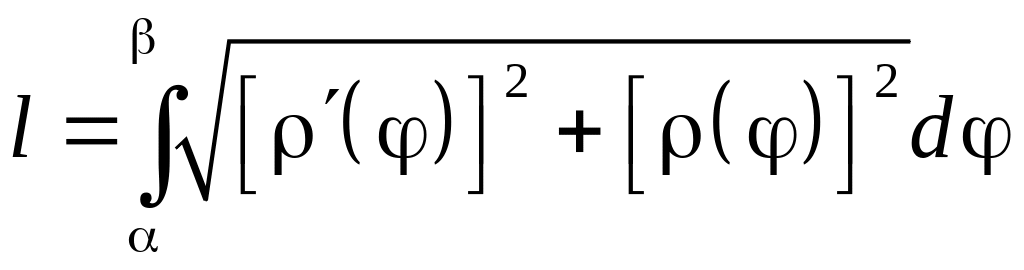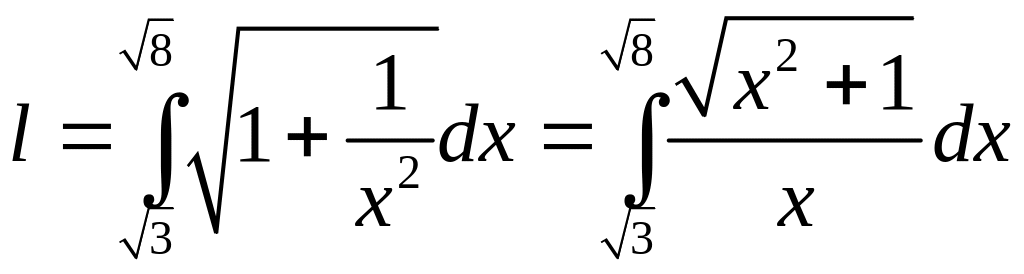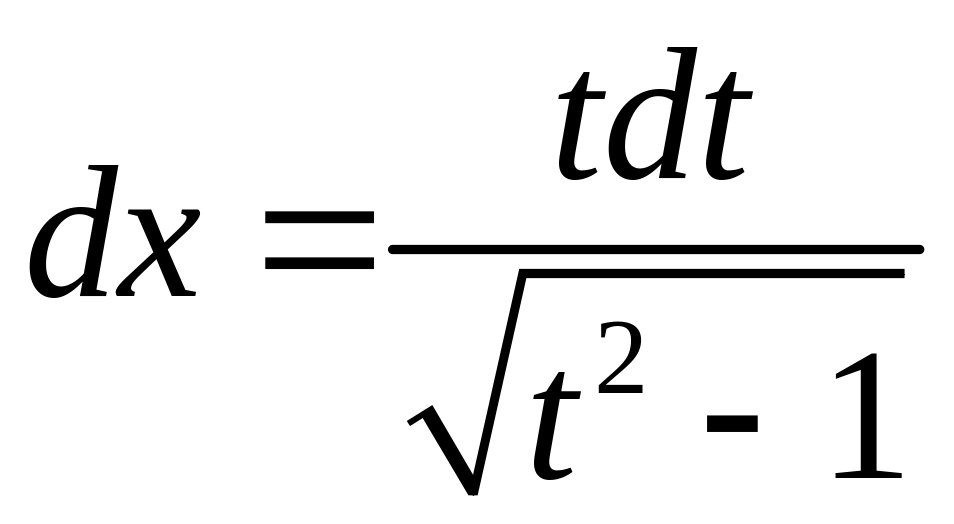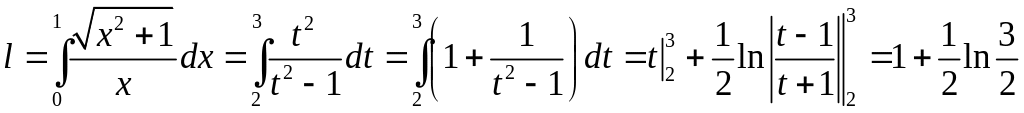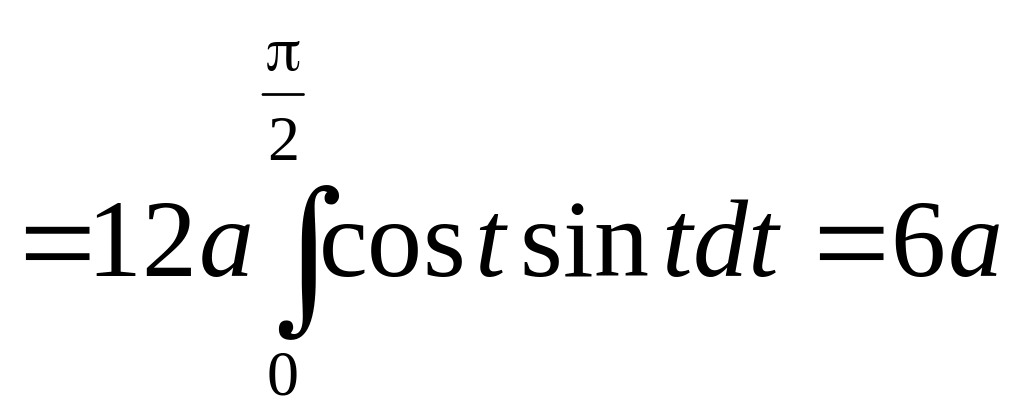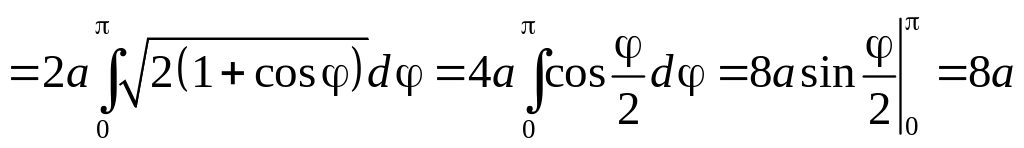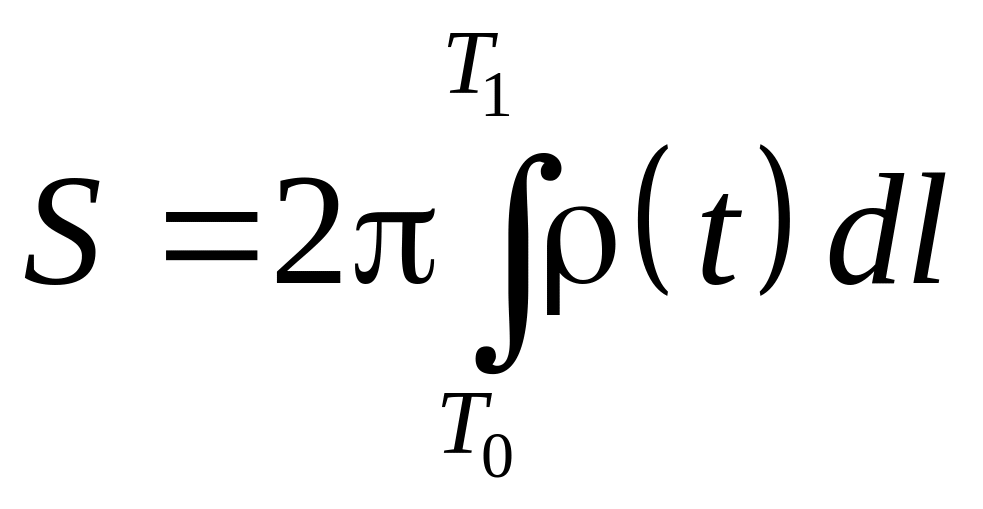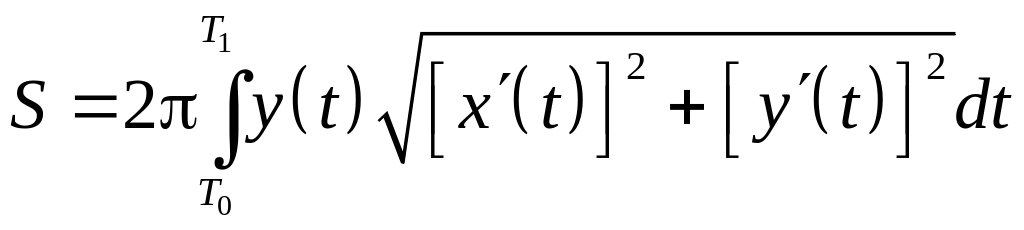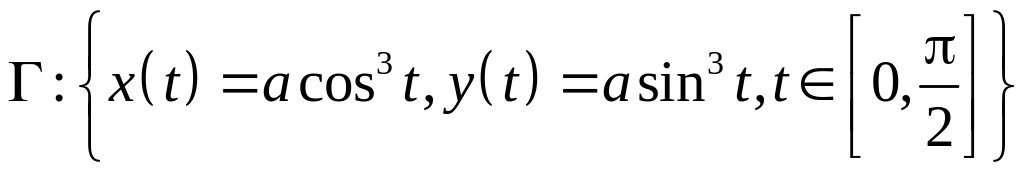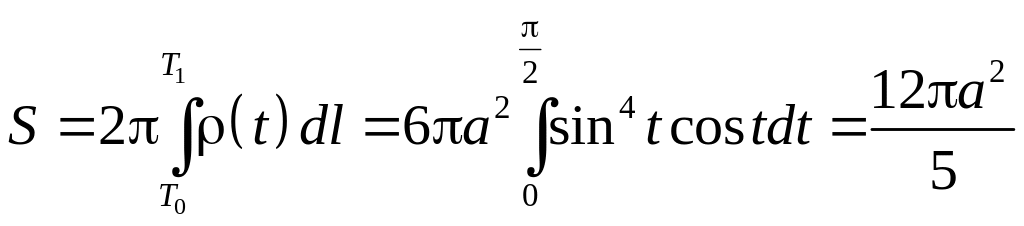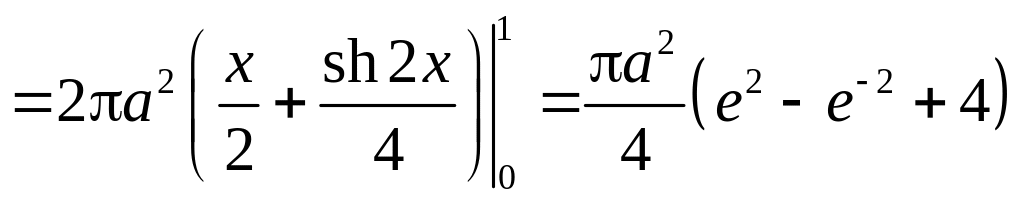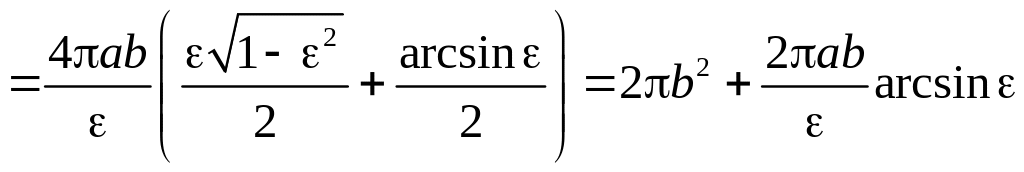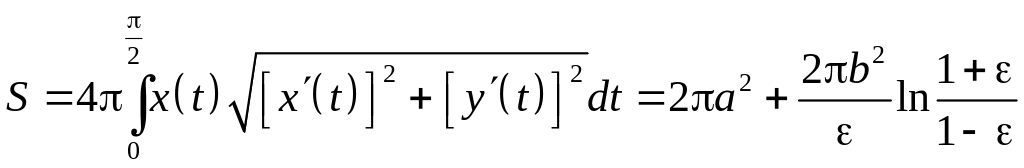Эллипсоид можно получить путем деформации сферы. Проще говоря, эллипсоид — это вытянутая либо сплюснутая сфера.
Онлайн-калькулятор объема эллипсоида
Эллипсоид обладает полуосями. Исходя из того, что эллипсоид — пространственное тело, то полуосей у него будет ровно на единицу больше, чем у эллипса, то есть, три.
Каноническое уравнение эллипсоида может быть записано так:
x2a2+y2b2+z2c2=1frac{x^2}{a^2}+frac{y^2}{b^2}+frac{z^2}{c^2}=1,
где a,b,ca, b, c — полуоси эллипсоида;
x,y,zx, y, z — координаты точек, принадлежащих эллипсоиду.
Полуоси эллипсоида – это положительные величины:
a>0,b>0,c>0a>0, b>0, c>0
Если:
a>b>ca>b>c,
то aa — это большая полуось, bb — средняя, а cc — малая.
Формула объема эллипсоида через его полуоси
Для вычисления объема эллипсоида существует такая формула:
V=43⋅π⋅a⋅b⋅cV=frac{4}{3}cdotpicdot acdot bcdot c
Полезно заметить, что эта формула переходит в формулу для объема шара, если положить:
a=b=c=Ra=b=c=R,
где RR — объем данного шара.
Рассмотрим несколько примеров.
Даны полуоси эллипсоида, численно равные 3 см3text{ см}, 4 см4text{ см}, 5 см5text{ см}. Определите его объем.
Решение
a=3a=3
b=4b=4
c=5c=5
По формуле вычисляем:
V=43⋅π⋅a⋅b⋅c=43⋅π⋅3⋅4⋅5≈251.2 см3V=frac{4}{3}cdotpicdot acdot bcdot c=frac{4}{3}cdotpicdot 3cdot 4cdot 5approx251.2text{ см}^3
Ответ
251.2 см3.251.2text{ см}^3.
Даны две полуоси эллипсоида – 6 см6text{ см} и 8 см8text{ см}. Найдите его объем, если известно, что третья полуось равна длине гипотенузы треугольника, катетами которого являются две вышеописанные полуоси.
Решение
Неважно, как обозначить данные полуоси, поэтому пусть:
b=8b=8
c=6c=6
Для нахождение неизвестной полуоси эллипсоида воспользуемся теоремой Пифагора для прямоугольного треугольника. По условию задачи, неизвестная полуось aa является гипотенузой прямоугольного треугольника, а полуоси bb и cc выступают катетами этого треугольника. Тогда:
a2=b2+c2a^2=b^2+c^2
a2=82+62a^2=8^2+6^2
a2=64+36a^2=64+36
a2=100a^2=100
a=10a=10
Теперь найдем объем эллипсоида по формуле:
V=43⋅π⋅a⋅b⋅c=43⋅π⋅10⋅8⋅6≈2009.6 см3V=frac{4}{3}cdotpicdot acdot bcdot c=frac{4}{3}cdotpicdot 10cdot 8cdot 6approx2009.6text{ см}^3
Ответ
2009.6 см3.2009.6text{ см}^3.
Не знаете, где можно заказать контрольную работу? Наши эксперты окажут вам оперативную помощь в решении контрольных работ по объемам фигур!
Тест по теме “Объем эллипсоида”
Пусть
— стандартная относительно оси
область. Если ось
не пересекает область
,
то объем тела, образованное вращением
области
вокруг оси
равна
,
если ось
не пересекает область
,
то объем тела, образованное вращением
области
вокруг оси
равна
.
Если область
ограничена непрерывной замкнутой
кривой, заданной параметрически
,
причем при изменении
от
до
кривая
проходится так, что область
остается слева. Если область
не пересекается с соответствующей осью
координат и функции
и
непрерывно дифференцируемы на
,
то
,
.
Примеры:
6.2.1. Вычислить
объём тела, полученного вращением
параболы
вокруг осей
и
,
ограниченного прямыми
и
.
n
Так как
,
,
,
то объем тела, полученного вращением
параболы вокруг
,
вокруг
.
6.2.2. Вычислить
объем удлиненного и укороченного
эллипсоида, образованного вращением
эллипса
вокруг осей абсцисс (удлиненный эллипсоид)
и ординат (укороченный эллипсоид).
n
Используем параметрическое параметрическое
представление эллипса
,
.
Вычисляя производные
,
.
Тогда, при изменении
от
до
,
получаем для удлиненного эллипса

,
а для укороченного
.
Обратим внимание,
что в случае шара
,
его объем равен
.
6.2.3. Вычислить
объем тела, образованного вращением
астроиды
вокруг оси абсцисс.
n
Используя параметрическое представление
,
при изменении параметра
в пределах от
до
,
получаем:
,
,
а объем тела равен
.
6.3. Вычисление длины дуги кривой
Если плоская кривая
задана параметрически
,
,
причем
и
— непрерывно дифференцируемые функции,
то она имеет длину, вычисляемую по
следующей формуле
.
Если плоская кривая
– график непрерывно дифференцируемой
функции
и
,
то длина этой кривой вычисляется по
формуле
.
В полярных
координатах
.
Пусть задана дуга
кривой
и функции
непрерывно дифференцируемы на
,
то дифференциал функции длины дуги
называется дифференциалом дуги и
вычисляется по одной из формул:
,
,
.
Примеры:
6.3.1.
Вычислить длину линии
от
до
.
n
Так как
,
то искомая длина равна
.
Положим
,
отсюда
,
.
Новые пределы интегрирования:
,
.
Тогда:
6.3.2. Вычислить
длину астроиды, заданной уравнением
(
,
).
n
Используя параметрическое представление
при изменении параметра
в пределах от
до
(первая четверть) и находя производные
и
,
Получаем
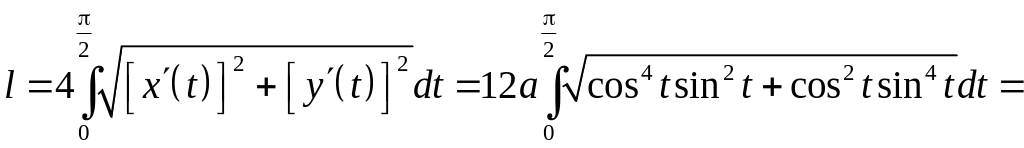
.
6.3.3.
Вычислить
длину кардиоиды,
заданной уравнением
.
n
Так как
,
то
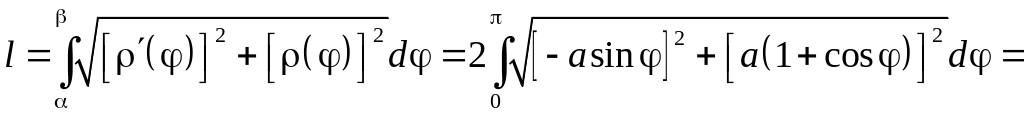
.
6.4. Вычисление площади поверхности вращения
Пусть задана
кривая
,
и прямая
,
являющаяся осью вращения. Тогда площадь
поверхности
полученная вращением
вокруг оси
вычисляется
по формуле
,
где
— расстояние от точки
,
лежащей на кривой
,
до оси вращения
,
а
— дифференциал дуги
.
То есть если
поверхность:
а) получается при
вращении кривой
,
вокруг оси
,
то в качестве параметра вводится
переменная
,
,
и искомая площадь равна
.
б) получается при
вращении параметрически заданной кривой
вокруг оси
,
то
,
,
а её площадь равна
.
в) получается при
вращении кривой заданной в полярных
координатах
вокруг полярной оси, то
,
,
площадь находится по формуле
.
Примеры:
6.4.1. Вычислить
площадь поверхности, образованной
вращением астроиды, заданной уравнениями
,
вокруг оси абсцисс.
n
Так как
,
,
то площадь
поверхности, получаемой при вращении
астроиды равна
6.4.2. Вычислить
площадь поверхности получаемой вращением
цепной линии
(такая поверхность называется катеноидом)
вокруг оси абсцисс и ограниченного
двумя плоскостями
и
,
перпендикулярными оси абсцисс.
n
Напомним, что
,
,
,
.
Тогда площадь
поверхности катеноида будет равна
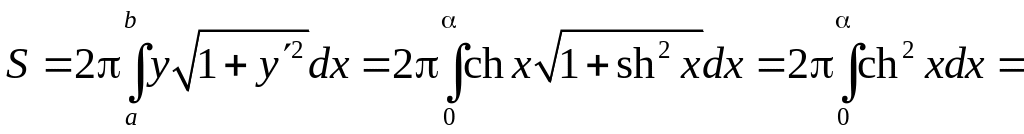
.
6.4.3. Найти
площадь поверхности вращения удлиненного
и укороченного эллипсоида (см. задачу
6.2.2.).
n
Используем параметрическое параметрическое
представление эллипса
,
.
Вычисляя производные
,
.
Тогда, при изменении
от
до
,
получаем для удлиненного эллипсоида
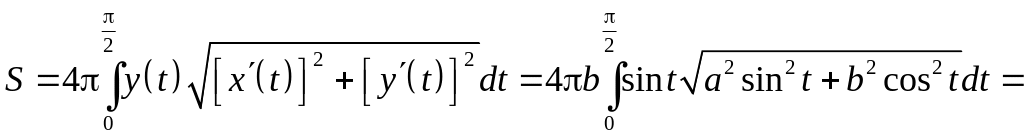
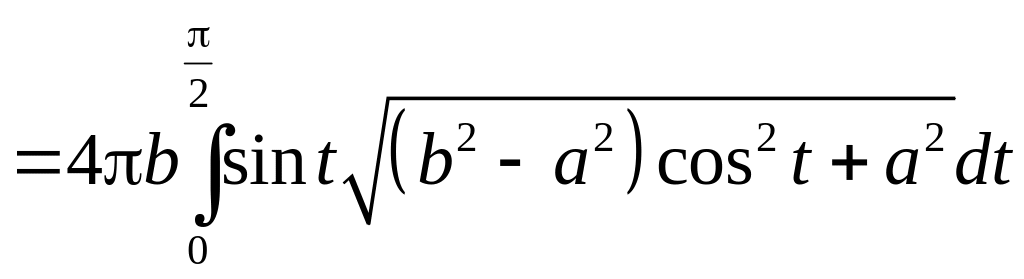
Обозначая
— эксцентриситет эллипса, получаем:
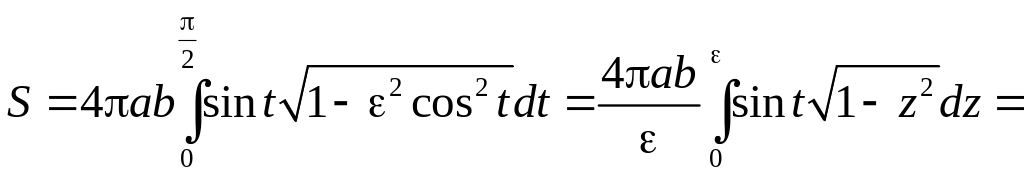
.
Аналогично, для
укороченного эллипсоида
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Эллипсоид не является телом вращения, тем не менее, его поверхность можно представить в виде алгебраического уравнения второго порядка, что дает возможность вывести формулу его объема через полуоси эллипсоида a, b и c, которые в трехмерной системе координат ложатся на оси x, y и z соответственно. Поскольку эллипсоид берет свое происхождение от сферы, то можно провести закономерную связь между их объемами. Более того, одна формула вытекает из другой и они являются повторением друг друга с различными заданными переменными, с той лишь разницей, что у сферы все три полуоси равны между собой и представлены радиусом окружности, которая вращается вокруг своей оси. Сплюснув окружность в двух направлениях, мы получим эллипсоид, у которого полуоси различны. Заменив каждый радиус в формуле объема сферы на полуоси эллипсоида, получим формулу его объема через полуоси: