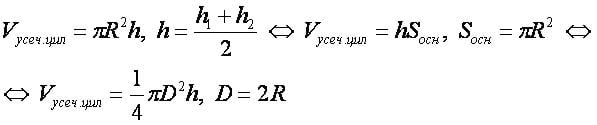Как найти объем усеченного цилиндра

Числовые значения в таблице заполняются числом (5; 5.16; -3.12), либо математическим выражением (5/7; (1-5)*2.13)

Введите радиус или диаметр *:

Введите высоты * и (или) угол:

Без макс. и мин. высоты можно посчитать только площади боковой поверхности и основания и объём

Или введите одну из высот и угол сечения (рис.)

Округление:

Построение развёртки:

* — обязательно заполнить

Определение площади поверхности и объема усеченных цилиндров и призм

Джон Рэй Куэвас

Что такое усеченный цилиндр?

Усеченный круговой цилиндр, также известный как цилиндрический сегмент, представляет собой твердое тело, образованное пропусканием непараллельной плоскости через круговой цилиндр. Некруглое верхнее основание наклонено к круглому сечению. Если круговой цилиндр является правильным цилиндром, то каждая правая часть представляет собой круг, имеющий такую ​​же площадь, что и основание.

Пусть K — площадь правого сечения, а h ₁ и h _{2 —} самый короткий и самый длинный элемент усеченного цилиндра соответственно. Объем усеченного кругового цилиндра определяется формулой, приведенной ниже. Если усеченный цилиндр представляет собой правильный круговой цилиндр радиуса r, объем можно выразить через радиус.

V = K

V = πr ²

Усеченные цилиндры

Джон Рэй Куэвас

Что такое усеченная призма?

Усеченная призма — это часть призмы, образованная путем прохождения плоскости, не параллельной основанию и пересекающей все боковые края. Поскольку плоскость усечения не параллельна основанию, сформированное твердое тело имеет два непараллельных основания, которые являются многоугольниками с одинаковым количеством ребер. Боковые края не совпадают, а боковые грани представляют собой четырехугольники (прямоугольники или трапеции). Если отрезанная призма — это правая призма, то боковые грани — правильные трапеции. Общая площадь поверхности усеченной призмы — это сумма площадей двух многоугольных оснований и правых трапециевидных граней.

В общем, объем усеченной призмы равен произведению площади ее правого сечения на среднее значение длин ее боковых краев. K — площадь правого сечения, L — средняя длина боковых краев. Для усеченной призмы правильное сечение равно площади основания. Объем усеченной призмы определяется формулой ниже. K — это B, умноженное на значение sinθ, L равно средней длине его боковых краев, а n — количество сторон основания.

V = KL

V = BL

Усеченные призмы

Джон Рэй Куэвас

Задача 1. Площадь поверхности и объем усеченной треугольной призмы.

Усеченная правая призма имеет равностороннее треугольное основание, одна сторона которого составляет 3 сантиметра. Боковые края имеют длину 5 см, 6 см и 7 см. Найдите общую площадь поверхности и объем усеченной правой призмы.

Площадь и объем усеченной треугольной призмы.

Джон Рэй Куэвас

Решение

а. Так как это усеченная справа призма, все боковые грани перпендикулярны нижнему основанию. Это делает каждую боковую грань призмы правильной трапецией. Вычислить для ребер AC, AB и BC верхнего основания, используя заданные в задаче меры.

AC = √3 ² + (7-5) ²

AC = √13 сантиметров

АВ = √3 ² + (7-6) ²

AB = √10 сантиметров

BC = √3 ² + (6-5) ²

AB = √10 сантиметров

б. Вычислите площадь треугольника ABC и треугольника DEF, используя формулу Герона.

s = (a + b + c) / 2

s = (√13 + √10 + √10) / 2

s = 4,965

_АВС = √4.965 (4,965 — √13) (4,965 — √10) (4,965 — √10)

A _ABC = 4,68 см ²

A _DEF = 1/2 (3) ² (sin (60 °))

A _DEF = 3,90 см ²

c. Вычислите площадь трапециевидных граней.

_ACED = 1/2 (7 + 5) (3)

A _ACED = 18 см ²

_BCEF = 1/2 (6 + 5) (3)

_BCEF = 16,5 см ²

_ABFD = 1/2 (7 +6) (3)

A _ABFD = 19,5 см ²

d. Найдите общую площадь усеченной призмы, суммируя все площади.

TSA = B ₁ + B ₂ + LSA

TSA = 4,68 + 3,90 + 18 +16,5 +19,5

TSA = 62,6 см ²

е. Найдите объем усеченной правой призмы.

V = BL

V = 3,90

V = 23,4 см ³

Окончательный ответ: общая площадь поверхности и объем усеченной правой призмы, приведенные выше, составляют 62,6 см ² и 23,4 см ³ соответственно.

Задача 2: объем и поперечная площадь усеченной прямоугольной призмы

Найдите объем и поперечную площадь усеченной прямоугольной призмы с краем основания 4 фута. Боковые края имеют размеры 6 футов, 7 футов, 9 футов и 10 футов.

Объем и поперечная площадь усеченной прямоугольной призмы.

Джон Рэй Куэвас

Решение

а. Поскольку это прямоугольная усеченная призма, все боковые грани перпендикулярны нижнему основанию. Это делает каждую боковую грань призмы правильной трапецией. Вычислите края верхнего квадратного основания, используя указанные в задаче меры.

S ₁ = √4 ² + (10-9) ²

S ₁ = √17 футов

S ₂ = √4 ² + (9-6) ²

S ₂ = 5 футов

S ₃ = √4 ² + (7-6) ²

S ₃ = √17 футов

S ₄ = √4 ² + (10-7) ²

S ₄ = 5 футов

б. Вычислите площадь трапециевидных граней.

А ₁ = 1/2 (10 + 9) (4)

A ₁ = 38 футов ²

А ₂ = 1/2 (9 + 6) (4)

A ₂ = 30 футов ²

А ₃ = 1/2 (7 +6) (4)

А ₃ = 26 футов ²

А ₄ = 1/2 (7 + 10) (4)

А ₄ = 34 фута ²

c. Вычислите общую боковую площадь, получив сумму всех площадей боковых поверхностей.

TLA = А ₁ + А ₂ + А ₃ + А ₄

TLA = 38 + 30 + 26 + 34

TLA = 128 футов ²

е. Найдите объем усеченной прямоугольной призмы.

V = BL

V = 4 ²

V = 128 футов ³

Окончательный ответ: общая площадь поверхности и объем усеченной правой квадратной призмы, приведенные выше, составляют 128 футов ² и 128 футов ³ соответственно.

Задача 3: объем правого кругового цилиндра

Покажите, что объем усеченного правого кругового цилиндра равен V = πr ².

Объем правого кругового цилиндра.

Джон Рэй Куэвас

Решение

а. Упростите все переменные данной формулы для объема. B обозначает площадь основания, а h ₁ и h ₂ обозначают самый короткий и самый длинный элементы усеченного цилиндра, показанного выше.

B = площадь круглого основания

B = πr ²

б. Разделите усеченный цилиндр на два твердых тела так, чтобы клиновая часть имела объем, равный половине объема верхнего цилиндра высотой h ₂ — h ₁. Объем верхнего цилиндра обозначен V ₁. С другой стороны, нижняя часть представляет собой цилиндр высотой h ₁ и объемом V ₂.

V = (1/2) V ₁ + V ₂

V ₁ = B (h ₂ — h ₁)

V ₂ = B xh ₁

V = (1/2) (B (h ₂ — h ₁)) + (B xh ₁)

V = (1/2) (B xh ₂) — (1/2) (B xh ₁) + (B xh ₁)

V = B

V = πr ²

Окончательный ответ: объем усеченного правого кругового цилиндра равен V = πr ².

Задача 4: Полная площадь поверхности усеченной прямоугольной призмы

Блок земли в виде усеченной правой призмы имеет квадратное основание с размером ребер 12 сантиметров. Два смежных боковых края имеют длину 20 см каждый, а два других боковых края имеют длину 14 см каждый. Найдите общую площадь поверхности блока.

Общая площадь усеченной прямоугольной призмы.

Джон Рэй Куэвас

Решение

а. Поскольку это прямоугольная усеченная призма, все боковые грани перпендикулярны нижнему основанию. Это делает каждую боковую грань призмы правильной трапецией. Вычислите края верхнего квадратного основания, используя указанные в задаче меры.

S ₁ = √12 ² + (20-20) ²

S ₁ = 12 сантиметров

S ₂ = √12 ² + (20 — 14) ²

S ₂ = 6√5 сантиметров

S ₃ = √12 ² + (14 — 14) ²

S ₃ = 12 сантиметров

S ₄ = √12 ² + (20 — 14) ²

S ₄ = 6√5 сантиметров

б. Вычислите площадь нижнего квадратного основания и верхнего прямоугольного основания.

_{ВЕРХНИЙ} = 12 х 6√5

_{ВЕРХНИЙ} = 72√5 см ²

_НИЖНИЙ = 12 х 12

_НИЖНИЙ = 144 см ²

б. Вычислите площадь прямоугольной и трапециевидной граней данной усеченной прямоугольной призмы.

А ₁ = 20 х 12

A ₁ = 240 см ²

А ₂ = 1/2 (20 + 14) (12)

A ₂ = 204 см ²

А ₃ = 14 х 12

А ₃ = 168 см ²

А ₄ = 1/2 (20 + 14) (12)

А ₄ = 204 см ²

d. Найдите общую площадь поверхности усеченной квадратной призмы, суммируя все площади.

TSA = _{ВЕРХНИЙ} + _НИЖНИЙ + LSA

TSA = 72√5 + 144 + 240 + 204 + 168 + 204

TSA = 1120,10 см ²

Окончательный ответ: Общая площадь поверхности данной усеченной квадратной призмы составляет 1120,10 см ².

Другие темы о площади поверхности и объеме

• Как рассчитать приблизительную площадь фигур неправильной формы с помощью правила Симпсона 1/3

  Узнайте, как приблизить площадь фигур неправильной формы с помощью правила 1/3. В этой статье рассматриваются концепции, проблемы и решения о том, как использовать правило Симпсона 1/3 для аппроксимации площади.

• Как вычислить

  площадь поверхности и объем призм и пирамид Это руководство научит вас определять площадь поверхности и объем различных многогранников, таких как призмы, пирамиды. Есть примеры, чтобы показать вам, как решать эти проблемы шаг за шагом.

© 2020 Луч

Объём усечённого цилиндра — это объём цилиндра со средней высотой усечённого цилиндра.

Рассмотрим прямые круговые усечённые цилиндры без сечения основания.

Обозначения[править]

Введём обозначения:

R — радиус основания цилиндра;

D — диаметр основания цилиндра;

h — средняя высота усечённого цилиндра;

h₁ — наименьшая высота усечённого цилиндра;

h₂ — наибольшая высота усечённого цилиндра;

V_{усеч.цил} — объём усечённого цилиндра.

Формула[править]

Невозможно разобрать выражение (синтаксическая ошибка): {displaystyle V_{усеч.цил} = pi R^2h, h = frac{h_1+h_2}{2} iff V_{усеч.цил} = hS_{осн}, S_{осн} = pi R^2 iff}

Невозможно разобрать выражение (синтаксическая ошибка): {displaystyle iff V_{усеч.цил} = frac{1}{4}pi D^2h, D = 2R}

См. также[править]

• Площадь поверхности усечённого цилиндра

Другие формулы[править]

• объём фигуры вращения;
• объём шара;
• объём цилиндра;
• объём конуса;
• объём усечённого цилиндра;
• объём усечённого конуса;
• объём шарового сегмента;
• объём шарового сектора;
• объём шарового слоя;
• объём шарового клина;
• объём цилиндрической трубы;
• объём цилиндрического копыта;
• объём конусного копыта;
• объём шаровой бочки;
• объём круговой бочки;
• объём тора;
• объём кокона;
• объём купола;
• объём сфероида.

Литература[править]

• Бронштейн М. Н., Семендяев К. А. Справочник по математике — М., 1956, стр.175.

Объём эллиптического (овального) цилиндра

Чтобы посчитать объём эллиптического (овального) цилиндра воспользуйтесь нашим онлайн калькулятором:

Онлайн калькулятор

Просто введите данные и получите ответ.

Теория

Объём эллиптического цилиндра через полуоси

Объём эллиптического цилиндра через оси

См. также

several hours ago, I saw the problem involving geometry. The problem is tell about truncated cylinder.

I want to know how to derive the formula of volume and its surface area without calculus, but still don’t get it.

I’ve just can found the definition and the volume without proof from:

http://encyclopedia2.thefreedictionary.com/Truncated+Cylinder

Truncated cylinder is the geometric solid produced when a cylinder is cut by a plane that is not parallel to the base.

The volume of a truncated circular cylinder is $V = frac{pi r^2(h1 + h2)}{2}$, where $h1$ and $h2$ are the lengths of the longest and shortest elements of the cylinder and $r$ is the radius of the base.

But, there are no proof here, how can I prove this formula? And also is it possible to find the surface area for this kind of the cylinder?

Edit: I’ve just found the formula of its surface area(without proof too). Here is the link:

http://www.math24.net/cylinder.html

But, how can I got the Area of the bases of a truncated cylinder? In this formula, the root form is appears. How can I got the root form?

Thanks