Как найти объем тела в метрах кубических - Avtoru.top

Один метр кубический является единицей объема. Чтобы найти объем какого-то предмета, имеющего КУБИЧЕСКУЮ форму (например, параллелепипед), нужно его длину (в метрах) умножить на ширину (тоже в метрах) и умножить на высоту (опять в метрах). Логично, не правда ли, что метр, умноженный сам на себя три раза превращается в метр кубический!

Если требуется посчитать объем предмета НЕ КУБИЧЕСКОЙ формы (например, шар, призма, конус), то для вычисления их объема есть специальные формулы. Если они вам нужны, то советую посмотреть учебник по геометрии.

автор вопроса выбрал этот ответ лучшим

Ксарфакс
[156K]

5 лет назад

Думаю, всем понятно, что формула расчёта объёма в кубических метрах для каждой геометрической фигуры будет разной.

Поэтому нужно произвести все необходимые измерения, а затем воспользоваться соответствующей формулой. Если фигура имеет неправильную формулу, то разбиваем её на несколько стандартных фигур, а затем складываем их объёмы между собой.

Нужно помнить, что все измерения проводятся именно в метрах. Например, если высота объекта 70 см, то её нужно перевести в метры: 70 см = 0,7 м.

Самый простейший пример — объём помещения

Для того, чтобы посчитать объём, нужно воспользоваться формулой нахождения объёма прямоугольного параллелепипеда.

V = abc.

a — длина, b — ширина, c — высота.

Таким образом, измеряем длину / ширину / высоту комнаты, а затем перемножаем эти значения между собой.

Если вы знаете площадь, то посчитать объём ещё проще — достаточно измерить высоту и умножить это значение на данное значение.

Например, длина комнаты = 6 м, ширина = 5 м, высота = 2,5 м.

V = 6 * 5 * 2,5 = 75 м³.

Nelli4ka
[114K]

5 лет назад

Для примера возьмем прямоугольник и параллелепипед.

Прямоугольник лежит на плоскости, и мы можем найти либо его периметр (т.е. длину всех сторон данной фигуры), либо его площадь, которая будет выражаться, скажем, в сантиметрах или метрах квадратных.

Параллелепипед — фигура трехмерного пространства, у нее есть помимо ширины и длины еще и высота. Когда значения высоты, длины и ширины умножаются друг на друга, находится объем трехмерной фигуры, которая уже будет выражаться не в квадратных, а в кубических сантиметрах, метрах и т.д., но для каждого некубического случая существует своя индивидуальная формула.

Galina7v7
[120K]

7 лет назад

Если ваш вопрос трактовать так: «как посчитать объём 1 метра кубического , то

V = 1м * 1 м = 1м = 1 м ^3 (1 метр кубический ) , и это единица измерения объёма в системе СИ.

Если вас интересует тело в форме параллелепипеда ,где все соседние ребра перпендикулярны друг другу , то объём такого тела определяется путём произведения : длина *ширина * высота.

ОБЪЁМ ТЕЛА = ДЛИНА (м) х ШИРИНА (м) х ВЫСОТА (м)

Для того,чтобы получить объём в м^3 нужно все 3 параметра тоже выразить в метрах.

Zolotynka
[551K]

5 лет назад

В метрах кубических можно высчитать объем предмета, который представляет собой форму куба. Для этого следует воспользоваться формулой: длина*ширина*высота.

Данная формула имеет важное практическое значение. Рассмотрим на примере:

Предположим, нам нужно рассчитать, расход бетона для того, чтобы сделать пол в сарае, размер которого: ширина 2.0 м, длина 2.0 м, а желаемая толщина бетона — 100 мм.

Формула для расчета объема бетона в м3 будет выглядеть следующими образом:

2,0 × 2,0 × 0,1 = 0.4m3

Математика обязательный предмет в школьной программе, но знания уходят, забываются формулы, как проводить вычисления уже не каждый вспомнит, остается в голове то, что используется нами ежедневно, и на работе требуется все время, поэтому формула расчета кубического метра может придти в голову не сразу, и придется искать эту информацию, для тех, кому нужно — длину умножить на ширину и умножить на высоту.

Kerbal Space Program
[23.1K]

6 лет назад

Крайне просто. Для этого достаточно брать длины и расстояния в метрах: будь то длина, высота и ширина или же радиус, при вычислении объема круга или цилиндра.

Например, имеем:

Параллелепипед длиной 1245 см, шириной 3 см и высотой 25 см.

Эти длины переведем в метры и получим:

длина: 1,245 метра.
ширина: 0,03 метра.
высота: 0,25 метров.

Считаем теперь объем: V=1,245*0,03*0,25=0,00933 метра кубических.

moreljuba
[62.5K]

5 лет назад

Посчитать объём в метрах кубических вы вполне спокойно можете. Для это вам необходимо иметь представление о значениях для таких величин как высота, ширина (толщина) и длина. Переводите в метры и перемножаете эти три составляющие и получаете в результате объём в метрах кубических.

FantomeRU
[13.3K]

5 лет назад

Чтобы вычислить объем необходимо умножить длину на ширину и на высоту. При этом, чтобы искомый результат был в кубических метрах, сначала нужно все стороны данного предмета выразить в метрах и только потом перемножать.

vksvovko
[1.6K]

6 лет назад

Один из распространенных способов найти объем предмета неправильной формы — это налить воду в измерительный сосут и опустить туда предмет. далее смотрим сколько он вытеснил воды и легко подсчитываем объем в м3.

EvgeniyAlekseevich
[464]

7 лет назад

Высоту, выраженную в м3, умножить на длину и умножить на ширину.

Знаете ответ?

Источник

Загрузить PDF

Кубические метры (м³) — это единица измерения объема, равная объему куба, стороны которого равны одному метру. Кубические метры являются предпочтительной единицей измерения при различных работах, например, при заливке бетона. Объем любого прямоугольного пространства длиной «L», шириной «W» и высотой «Н» вычисляется по формуле: Объем = L × W × H.

1
Измерьте все необходимые расстояния в метрах. Объем многих трехмерных фигур легко вычислить по соответствующим формулам. Однако все значения, подставляемые в формулы, должны измеряться в метрах. Таким образом, перед подстановкой значений в формулу убедитесь, что все они измеряются в метрах, или что вы конвертировали другие единицы измерения в метры.
- 1 мм = 0,001 м
- 1 см = 0,01 м
- 1 км = 1000 м
2
Для вычисления объема прямоугольных фигур (прямоугольный параллелепипед, куб) используйте формулу: объем = L × W × H (длину умножить на ширину умножить на высоту). Эту формулу можно рассматривать как произведение площади поверхности одной из граней фигуры на ребро, перпендикулярное этой грани.
- Например, вычислим объем комнаты длиной 4 м, шириной 3 м и высотой 2,5 м. Для этого просто умножим длину на ширину и на высоту:
  - 4 × 3 × 2,5
  - = 12 × 2,5
  - = 30. Объем этой комнаты равен 30 м³.
- Куб – объемная фигура, у котрой все стороны равны. Таким образом, формулу для вычисления объема куба можно записать в виде: объем = L³ (или W³, или H³).
3
Для вычисления объема фигур в виде цилиндра используйте формулу: пи × R² × H. Вычисление объема цилиндра сводится к умножению площади круглого основания на высоту (или длину) цилиндра. Найдите площадь круглого основания, умножив число пи (3,14) на квадрат радиуса круга (R) (радиус — расстояние от центра окружности до любой точки, лежащей на этой окружности). Затем полученный результат умножьте на высоту цилиндра (H), и вы найдете объем цилиндра. Все значения измеряются в метрах.
- Например, вычислим объем колодца диаметром 1,5 м и глубиной 10 м. Разделите диаметр на 2, чтобы получить радиус: 1,5/2=0,75 м.
  - (3,14) × 0,75² × 10
  - = (3,14) × 0,5625 × 10
  - = 17,66. Объем колодца равен 17,66 м³.
4
Для вычисления объема шара используйте формулу: 4/3 х пи × R³. То есть вам нужно знать только радиус (R) шара.
- Например, вычислим объем воздушного шара диаметром 10 м. Разделите диаметр на 2, чтобы получить радиус: 10/2=5 м.
  - 4/3 х пи × (5)³
  - = 4/3 х (3,14) × 125
  - = 4,189 × 125
  - = 523,6. Объем воздушного шара равен 523,6 м³.
5
Для вычисления объема фигур в виде конуса используйте формулу: 1/3 х пи × R² × H. Объем конуса равен 1/3 объема цилиндра, который имеет такую же высоту и радиус.
- Например, вычислим объем конуса мороженного радиусом 3 см и высотой 15 см. Конвертируя в метры, получим: 0,03 м и 0,15 м соответственно.
  - 1/3 х (3,14) × 0,03² × 0,15
  - = 1/3 х (3,14) × 0.0009 × 0,15
  - = 1/3 × 0.0004239
  - = 0,000141. Объем конуса мороженного равен 0,000141 м³.
6
Для вычисления объема фигур неправильной формы используйте несколько формул. Для этого попробуйте разбить фигуру на несколько фигур правильной формы. Затем найдите объем каждой такой фигуры и сложите полученные результаты.
- Например, вычислим объем небольшого зернохранилища. Хранилище имеет цилиндрический корпус высотой 12 м и радиус 1,5 м. Хранилище также имеет коническую крышу высотой 1 м. Вычислив отдельно объем крыши и отдельно объем корпуса, мы можем найти общий объем зернохранилища:
  - пи × R² × H + 1/3 х пи × R² × H
  - (3,14) × 1,5² × 12 + 1/3 х (3,14) × 1,5² × 1
  - = (3,14) × 2,25 × 12 + 1/3 х (3,14) × 2,25 × 1
  - = (3,14) × 27 + 1/3 х (3,14) × 2,25
  - = 84,822 + 2,356
  - = 87,178. Объем зернохранилища равен 87,178 м³.
Реклама

1
Найдите площадь заливаемой бетоном поверхности. При заливке бетоном некоторого пространства (например, прямоугольной выемки в земле глубиной до нескольких десятков сантиметров) нет необходимости использовать сложные формулы для вычисления объема бетона, который вам потребуется. Вместо этого воспользуйтесь методом быстрого вычисления объема бетона. Начните с вычисления площади заливаемой поверхности.
- Все значения измеряются в метрах.
- Напомним, что площадь квадрата или прямоугольника вычисляется по формуле: площадь = длина × ширина. Площадь круга с радиусом r равна πr².
2

Определите толщину бетонной заливки. Для этого просто измерьте глубину выемки в земле. Так как выемка относительно неглубокая, используйте значения, измеренные в сантиметрах.
3
Разделите площадь на коэффициент, основанный на толщине бетона. Все, что вам нужно сделать, чтобы определить точный объем, это разделить площадь на определенное число — если толщина бетона будет небольшой, эта цифра будет больше. Если толщина бетона будет большой, то это число будет меньше. Ниже даны самые распространенные значения. Если ваша толщина не соответствует ни одной из представленных, перейдите к следующему шагу.
- Если толщина бетона равна 10,16 сантиметрам (0,1016 м), разделите площадь на 205,74, чтобы определить объем.
- Если толщина бетона равна 15,24 сантиметрам (0,1524 м), разделите площадь на 137,16, чтобы определить объем.
- Если толщина бетона равна 20,32 сантиметрам (0,2032 м), разделите площадь на 101,6, чтобы определить объем.
- Если толщина бетона равна 30,48 сантиметрам (0,3048 м), разделите площадь на 68,58, чтобы определить объем.
4
Вычислите объем бетона с помощью быстрого метода. Если в вашем случае толщина бетона не соответствует ни одному из приведенных выше примеров, не волнуйтесь — вычислить объем можно достаточно просто. Для этого вычислите площадь заливаемой поверхности, разделите ее на 100, а затем умножьте полученный результат на толщину бетона (в сантиметрах).
- Допустим, выемка в земле имеет размеры 10 м × 15 м и глубину 20 см.
  - 10 х 15 = 150
  - 150/100 = 1,5
  - 1,5 х 20 = 30. Нам понадобится 30 м³ бетона.
5

Купите немного больше бетона, чем нужно. Он пригодится в том случае, если ваши измерения не были точными. В конце концов, сухую бетонную смесь, которая останется, можно сохранить,а затем использовать в другом проекте.

Реклама

Советы

Метод быстрого вычисления объема бетона работает для заливаемых поверхностей любой правильной формы, но вычисляйте площадь заливаемой поверхности по соответствующей формуле.

Об этой статье

Эту страницу просматривали 673 815 раз.

Была ли эта статья полезной?

Источник

Посчитать объём коробки

Главная
/
Логистика
/
Посчитать объём коробки

Чтобы посчитать объем коробки или нескольких коробок воспользуйтесь нашим онлайн калькулятором:

Онлайн калькулятор

Расчет объема коробки

Длина коробки

Ширина коробки

Высота коробки

Объем коробки:

Просто введите длину, ширину и высоту коробки и узнаете её объём.

Расчет объема нескольких коробок

Количество коробок

шт
Длина коробки

Ширина коробки

Высота коробки

Объем одной коробки:

Общий объем всех коробок:

Теория

Коробка это прямоугольный параллелепипед, который имеет длину A, ширину B и высоту (глубину) C. Её объём считается по следующей формуле:

Формула

V = A⋅B⋅C

Пример

К примеру, возьмём коробку, у которой ширина равна 56 см, высота — 40 см, глубина — 32 см и посчитаем её объём:

V = 56⋅40⋅32 = 71680 см³

Если нам необходимо знать объём в кубометрах, нужно полученную цифру разделить на 1 000 000:

V = 71680/1000000 = 0.07168 ≈ 0.07 м³

См. также

Источник

Как посчитать кубические метры объемного тела? Кубический метр относится к единицам измерения физических величин.

Ученые из разных стран трудились много лет над созданием единой системы. К примеру, в разных странах существовали свои единицы для измерений расстояния: версты, футы, сажени, мили. В единой международной системе расстояние измеряют в метрах. Масса оценивается в килограммах вместо пудов, фунтов и так далее.

Кубический метр является производным, это справедливо и для других единиц.

Содержание

1 Как вычислить объемность тела?
2 Как рассчитать кубатуру материалов?
3 Способы перевода кубометров в другие кубические единицы

Как вычислить объемность тела?

Кубометр (м³) — это величина, равная объему куба, имеющего длину ребра в 1 метр. Метрами кубическими измеряются те физические тела, которые характеризуются 3 параметрами измерений:

длиной;
шириной;
высотой.

Чтобы определить величину объема тела, нужно перемножить все 3 параметра. Для подсчета меньших или больших объектов помимо метров кубических (м³) используются другие единицы: кубические миллиметры (мм³), кубические сантиметры (см³), кубические дециметры (дм³), кубические километры (км³), литры. Рассмотрим примеры расчета объемов тел разной конфигурации.

Пример 1. Найти объем коробки с длиной 2 м, шириной 4 м и высотой 3 м. Объем будет равен: 2 м х 4 м х 3 м = 24 м³

Пример 2. Найти объем цилиндра с диаметром основания 2 м и высотой 4 м. Вычисляем площадь круга, она равна πR². S = 3,14 х (1 м)² = 3,14 м². Находим объем: 3,14 м² х 3м = 9,42 м³.

Пример 3. Найти объем шара с диаметром 3 м. Чтобы посчитать кубические метры в шаре, вспомним формулу.

V = 4/3πR^3. Подставляем заданное значение и находим объем: 4/3 х 3,14 х (1,5 м)³ = 14,13 м^3.

Соответствия кубического метра

Пример 4. Как посчитать кубические метры в конусе с радиусом 4 м и высотой 5 м? Объем конуса находим по формуле V = 1/3πR²H = 1/3 х 3,14 х (4 м)² х 5 = 83,7 м^3.

Чтобы найти количество кубов в теле неправильной формы, нужно разделить его на составляющие с правильной формой. Найти их объемы и полученные результаты суммировать. Рассмотрим такой объект, как башня с конусообразной крышей.

Находим сначала кубатуру рабочего помещения, имеющего цилиндрическую форму, затем конусообразной крыши по приведенным выше формулам. Полученные результаты складываем.

Как рассчитать кубатуру материалов?

Чтобы узнать величину объема обрезной доски, следует сделать замеры трех ее величин: длины, ширины и толщины или высоты. Полученные значения перемножаем и получаем кубатуру одной доски. Затем этот объем умножаем на количество досок, находящихся в пачке.

Рассчитать кубатуру необрезной доски следует по-другому. Необрезанные доски чаще всего встречаются с толщиной 25 — 50 мм. Определить ее параметры сложно, поскольку она не совсем ровная.

Существует 3 способа подсчета кубатуры:

пакетно;
поштучно;
выборкой.

Выбрав 1 способ подсчета, нужно соблюсти такие условия:

передние торцы досок в пакете должны быть выровнены;
величина ширины пакета не должна по всей длине отклоняться от заданной;
недопустима укладка досок нахлестом;
недопустимо смещение досок внутрь пакета или наружу на величину, большую 100 мм.

Со стороны выровненных торцов замеряют высоту пакета h₁. Находим фактическую высоту h. Она будет равна h₁ — ab, где а — количество прокладок между досками, b — толщина одной прокладки.

Ширину пакета меряют по средней линии, разделяющей высоту пополам. Допустимая погрешность замеров — это ±10 мм.

Способ 2 говорит сам за себя. Производится замер каждой доски, подсчитываются все объемы и далее складываются.

Способ 3 применяют для крупных партий древесины. Ее кубатуру вычисляют по усредненным показателям, принятым для всей партии.

Точность расчета кубатуры необрезных пиломатериалов зависит от вида дерева, его типа и степени обработки. Часто бывает, что среди этих досок попадаются и обрезные.

Облегчить задачу подсчета объемов помогут специально разработанные таблицы — так называемые кубатурники.

Способы перевода кубометров в другие кубические единицы

Рассчитывая объемности, необходимо придерживаться одинаковых единиц замеров. Если данные представлены другими единицами, а конечный результат должен быть получен в кубах, то достаточно будет правильно сделать преобразование.

Если V измерен в мм³, см³, дм³, л, то в м³ переводим соответственно:

1 м³ = 1 мм³ х х 0, 000000001 = 1 мм³ х 10^-9;
1 м³ = 1 см³ х 0, 000001 = 1 см³ х 10^-6;
1 м³ = 1 дм³ х 0,001 = 1 дм³ х 10^-3. Такой же перевод применяют и для литров, поскольку в 1 л содержится 1 дм³.

Чтобы найти кубы вещества, зная его массу, нужно по таблице отыскать его плотность или определить вручную. Разделив заданную массу М (кг) на показатель плотности Р (кг/ м³), получим V материала (м³⁾.

Подсчитать кубические метры не составляет трудностей для человека, не имеющего математических наклонностей, несмотря на то что в каждом случае требуется разный подход.

Знания для определения объемов необходимы и специалистам, и обычным людям в повседневной жизни.

Источник

Изучение объемных фигур начинается со школы. В это время происходит знакомство с цилиндром, параллелепипедом, шаром, конусом и другими геометрическими телами. Одна из главных задача, которая сопровождает учеников, это вычисление объема фигур. Оперируя формулами, удается произвести расчет и получить ответ в метрах кубических (м³).

Чтобы вычислить объем, применяйте следующее правило – длину, ширину и высоту нужно перемножить между собой. Объем для каждой фигуры рассчитывается по специальной формуле, о которых, мы расскажем ниже.

Подписывайтесь на наш Telegram — канал

Содержание:

Как найти объем трехмерных объектов
Как найти объем для фигур цилиндрической формы
Как рассчитать объем треугольной пирамиды
Как посчитать объем куба
Как найти объем прямоугольного параллелепипеда
Как найти объем цилиндра
Как найти объем пирамиды

Как найти объем трехмерных объектов

Начнем с расчета для прямоугольных и квадратных фигур. Придерживайтесь инструкции и постарайтесь рассчитать самостоятельно, чтобы закрепить знания. Числа, указанные в описании, берутся в качестве примера. Вы можете производить другие расчеты.

Измеряем длину предмета в сантиметрах – 9. Сантиметры приходят на помощь, когда невозможно получить целое число в метрах .
Замеряем ширину в сантиметрах – 17.
Умножаем между собой длину и ширину 9 * 17 = 152 см²– получили площадь основания
Производим замер высоты – 28 см.
Умножаем площадь основания на высоту 152 см²* 28 см = 4256.

Полученное число необходимо перевести в кубические метры. Для этого конечный результат делим на 1.000.000. Пример будет выглядеть следующим образом – 4256 м³/1000000 = 0,004256 м³

Как найти объем для фигур цилиндрической формы

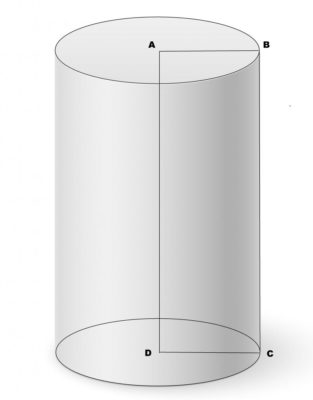
Цилиндр – это тело, ограниченное цилиндрической поверхностью с замкнутой направляющей и двумя параллельными плоскостями. Одним из видов цилиндра является призма.

Чтобы произвести вычисления нужно найти диаметр тела (ширина) одного круглого основания и полученное число поделить на 2. Допустим, диаметр основания равен 30 см.

Производим расчеты: 30 см / 2 = 15 см. Половина диаметра круга ‒ радиус.
Возводим полученный радиус в квадрат или умножаем самого на себя: 15 * 15 = 225 см².
Полученное число 225 см² – это квадрат радиуса. Эту цифру умножаем на число ПИ — 3,14. Например: 225 см²* 3,14 = 706,5 см².
Проводим новый замер, чтобы узнать расстояние между круглыми основаниями, допустим, оно равно 12 см.
Это число умножаем на площадь круглого основания: 706,5 см²* 12 см = 8 478 см³
Полученное значение и будет искомым объемом. Для перевода в кубические метры необходимо конечное число поделить на один миллион. Как мы делали в предыдущем примере.

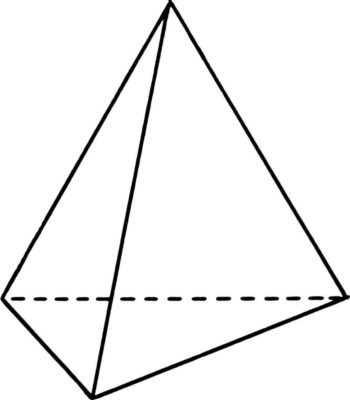
Как рассчитать объем треугольной пирамиды

Пирамида – это многогранник, где есть одна грань основания и боковые грани. Пирамиды бывают треугольные, четырехугольные и другие. Также есть правильная и усеченная пирамида. Объем для каждой фигуры рассчитывается по разным формулам.

Чтобы найти объём пирамиды замеряем длину стороны треугольника в основании пирамиды, предположим, что он равен 10 см.
Затем повторим то же самое, но с высотой – 13 см.
Длину высоты и стороны необходимо перемножить между собой и разделить на 2: 10 *13 = 130 см²/ 2 =65 см².
Замеряем высоту пирамиды – 33 см.
Умножаем площадь треугольника у основания на высоту и делим на 3. Например: 65 см²* 33 см =2 145 см²/ 3 = 715 см³.
Для преобразования в кубические метры производим деление конечного числа на миллион.

Расчёт четырехгранной пирамиды производится тем же принципом. Потренируйтесь, используя разные задачи. Чтобы все замеры происходили правильно, не забудьте обзавестись хорошей линейкой, также на помощь придёт калькулятор, который поможет перемножать числа между собой.

В интернете представлено много онлайн-калькулятор, они дают подсказку и позволяют без лишних трудностей рассчитать объём куба, цилиндра и других фигур. Перед началом пользования таких подсказок, необходимо обладать базовыми знаниями, чтобы быстрее разобраться в полученном результате.

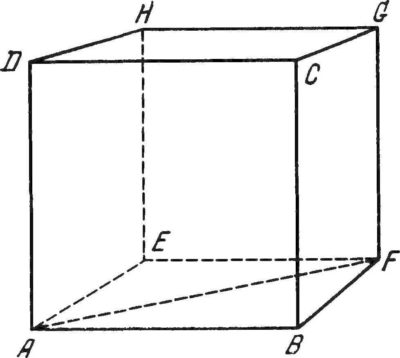
Как посчитать объем куба

Параллелепипед складывается из шести граней, которые являются параллелограммом. Все противоположные грани попарно равны и параллельны. Фигура получилась 4 диагонали, и все они пересекаются в одной точке, разделяют эту точку пополам. Параллелепипед, грани которого являются квадратами, будет называться кубом.

Все рёбра куба всегда будут равны. Для проведения вычислений, воспользуйтесь следующей формулой V = H³, где H ‒ высота ребра куба. Например: высота куба равняется ‒ 3 см, получается, что объем равен 3³= 27 см³.

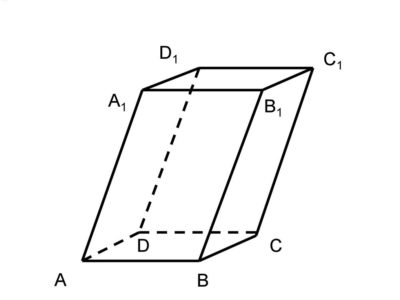
Как найти объем прямоугольного параллелепипеда

Прямоугольным параллелепипедом называется фигура, у которой все шесть граней прямоугольники. Для вычисления работает следующая формула:

V = SH = abc

Где H ‒ высота, S ‒ площадь основания, abc – ребра. Чтобы произвести расчеты и найти объём, необходимо узнать произведение площади основания на высоту. Например: 1 см * 2 см * 3 см = 6 см³

Советы по измерению:

Измерить стороны.
Каждая сторона параллелепипеда должна находиться в одинаковых единицах измерения.
Вычисляем площадь основания.
Умножаем площадь основания на высоту параллелепипеда.

Убедитесь, что перед вами параллелепипед, а не куб, так как в случае с кубом расчетная формула будет проще.

Как найти объем цилиндра

Цилиндр считать круглой фигурой, т.к. в его основании лежит круг. Чтобы произвести вычисления, необходимо узнать произведение площади основания на высоту. Для этого используется следующая формула:

V= π * r² * h

Где r ‒ радиус цилиндра, h – высота цилиндра. Чисто π – является константой и равно 3,14. Оно всегда одинаковое и не требует никаких измерений. Рассмотрим на примере:

3,14 * 2 см²* 5 см = 62.831853071796 = 63см³

Если вы не можете вычислить радиус, измерьте диаметр с помощью формулы преобразования.

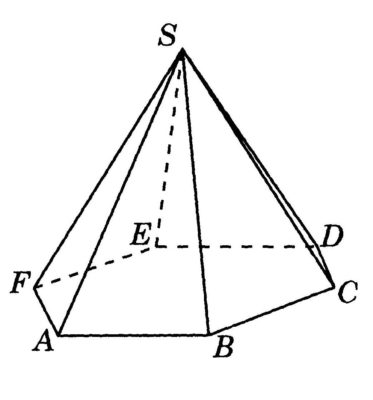
Как найти объем пирамиды

фото 6 — посчитать объём

Чтобы произвести расчет объема, нам нужно найти произведение площади основания на высоту. Для вычисления используется следующая формула:

V = S*h

Где S (A*B*C*D*E) – площадь основания пирамиды, а h ‒ высота пирамиды. Рассмотрим на примере:

V = 3 * 2 = 2 см³‒ это и будет являться объемом искомой геометрической фигуры.

Не забывайте, что пирамиды бывают усеченные, правильные, трех- и четырехугольные. Для каждого тела действуют свои расчеты, но важно начинать с основного и не упускать базовые знания, в дальнейшем все примеры будут базироваться именно на них.

Если какая-то формула осталась непонятной, лучше вернуться к этому и поупражняться ещё раз, доведя знание до автоматизма. Так решение задач не будет вызывать сложности. Постоянная практика ‒ это основа успешного результата.

Источник

ОБЪЁМ ТЕЛА = ДЛИНА (м) х ШИРИНА (м) х ВЫСОТА (м)

Советы

Об этой статье

Была ли эта статья полезной?

Посчитать объём коробки

Онлайн калькулятор

Расчет объема коробки

Расчет объема нескольких коробок

Теория

Формула

Пример

См. также

Как вычислить объемность тела?

Как рассчитать кубатуру материалов?

Способы перевода кубометров в другие кубические единицы

Содержание:

Как найти объем трехмерных объектов

Как найти объем для фигур цилиндрической формы

Как рассчитать объем треугольной пирамиды

Как посчитать объем куба

Как найти объем прямоугольного параллелепипеда

Как найти объем цилиндра

Как найти объем пирамиды

Не пропустите также: