В данной публикации мы рассмотрим формулу, с помощью которой можно вычислить объем сектора шара, а также пример решения задачи для демонстрации ее применения на практике.
- Определение сектора шара
- Формула для нахождения объема сектора шара
- Пример задачи
Определение сектора шара
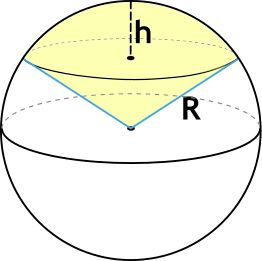
Сектор шара (или шаровый сектор) – это часть шара, состоящая из шарового сегмента и конуса, вершиной которого является центр шара, а основанием – основание соответствующего сегмента. На рисунке ниже сектор закрашен оранжевым цветом.
- R – радиус шара;
- r – радиус основания сегмента и конуса;
- h – высота сегмента; перпендикуляр от центра основания сегмента до точки на сфере.
Формула для нахождения объема сектора шара
Чтобы найти объем шарового сектора, необходимо знать радиус шара и высоту соответствующего сегмента.
Примечания:
- если вместо радиуса шара (R) дан его диаметр (d), последний следует разделить на два, чтобы найти требуемый радиус.
- π округленно равняется 3,14.
Пример задачи
Дан шар радиусом 12 см. Найдите объем шарового сектора, если высота сегмента, из которого состоит данный сектор, равняется 3 см.
Решение
Применим формулу, рассмотренную выше, подставив в нее известные по условиям задачи значения:
Шаровой сектор — это тело, которое можно получить при вращении сектора круга вокруг какого-либо из его радиусов, не пересекающего хорду этого кругового сектора.
Онлайн-калькулятор объема шарового сектора
Формула объема шарового сектора
Объем шарового сектора можно найти по такой формуле:
V=23⋅π⋅R2⋅hV=frac{2}{3}cdotpicdot R^2cdot h
RR —радиус шарового сектора;
hh — высота шарового сектора (проекция хорды, которая стягивает дугу кругового сектора на его ось вращения при получении таким образом шарового сектора).
Формула объема шарового сектора как объем пирамиды
Существует еще одна формула, с помощью которой можно найти искомый объем.
Она равна объему пирамиды, у которой площадь основания численно равна площади части сферической поверхности, которая вырезается сектором. Высота пирамиды равна радиусу шарового сектора.
V=13⋅R⋅SV=frac{1}{3}cdot Rcdot S
RR —радиус шарового сектора (высота соответствующей пирамиды);
SS — площадь основания пирамиды.
Разберем решение задач на данную тему.
Вычислите объем сектора шара, если его радиус равен 10 см10text{ см}, а высота – 7 см7text{ см}.
Решение
R=10R=10
h=7h=7
По первой формуле получаем:
V=23⋅π⋅R2⋅h=23⋅π⋅102⋅7≈1465 см3V=frac{2}{3}cdotpicdot R^2cdot h=frac{2}{3}cdotpicdot 10^2cdot 7approx1465text{ см}^3
Ответ
1465 см3.1465text{ см}^3.
Определить объем шарового сектора, если площадь основания соответствующей пирамиды равна 24 см224text{ см}^2, а ее высота равна 8 см8text{ см}.
Решение
S=24S=24
R=8R=8
Используем вторую формулу для объема шарового сектора:
V=13⋅R⋅S=13⋅8⋅24=64 см3V=frac{1}{3}cdot Rcdot S=frac{1}{3}cdot 8cdot 24=64text{ см}^3
Ответ
64 см3.64text{ см}^3.
Не знаете, где найти решение задач на заказ недорого? На нашем сайте есть профильные исполнители, которые помогут вам в этом!
Тест по теме “Объем шарового сектора”
Шаровой сектор – это часть шара, ограниченная кривой поверхностью шарового сегмента и конической
поверхностью, основанием которой служит основание сегмента, а вершиной центр шара. Другое
определение исходит из того, что шаровой сектор – тело вращения, т.е. образовано вращением
какой-либо плоской и ограниченной кривой геометрической фигуры вокруг лежащей в той же плоскости
оси. Объем шарового сегмента определяется рядом его размеров, ниже 2 формулы для вычисления
объема.
- Обьём шарового сектора через радиус шара и высоту шарового
сегмента - Обьём шарового сектора через радиус шара и угол между осью
и образующей конуса
Объём шарового сектора через радиус шара и высоту шарового сегмента
Зная радиус и высоту шарового сектора, можно найти его объем по следующей формуле:
V = 2/3 * π * R² * h
где R – радиус шара, h – высота шарового сегмента (или проекция хорды, стягивающей дугу сектора, на
ось вращения).
Цифр после
запятой:
Результат в:
Значение π примерно равно 3,14 – это числовая постоянная «число пи», одна из самых известных и чаще
всего использующихся, равная отношению длины окружности к ее диаметру; для всех окружностей это
отношение постоянно. «Пи» число иррациональное и трансцендентное, т.е. не может быть выражено
никакой рациональной дробью и не может быть корнем какого-либо многочлена с целыми
коэффициентами.
Пример. Радиус R = 5 м; h = 1,5 м. Рассчитываем объем: V = 2 * π * R² * h / 3 = 2 * 3,14 * 5² * 1,5 / 3 = 78,5 м³.
Объём шарового сектора через радиус шара и угол между осью и образующей конуса
При известном радиусе шара и угла между осью и образующей конуса можно так же найти объем шарового
сектора. Для это применяется формула:
V = 2/3 * π * R³ * (1 — cos α/2)
где R – радиус шара, cos α – угол между осью и образующей конуса.
Цифр после
запятой:
Результат в:
Пример. Вафельный рожок для мороженого, при заполнении мороженым имеющий форму
шарового сектора, имеет такие размеры: радиус R = 11 см, угол α = 26°. Необходимо рассчитать объем
мороженого в рожке при его заполнении. V = 2/3 * 3,14 * 11³ * (1 — cos 26º/2) = 71 см³.
Шаровой сектор – это геометрическое тело, возникающее при вращении сектора вокруг одного из его
радиусов. Форму, близкую к шаровому сектору, имеют, в качестве примера, современные воздушные шары и
мороженое в вафельном рожке.
Геометрия, 11 класс
Урок №14. Объем шара и его частей
Перечень вопросов, рассматриваемых в теме
- Доказательство теорем об объемах шара и его частей и площади сферы
- Определение частей шара
- Решение задач на нахождение объемов шара, его частей и площади сферы
Основная литература:
Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др. Геометрия 10-11 учебник для общеобразов. учрежд.: база и профильн. М: Просвещение.2009
Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. Геометрия. 10–11 классы : учеб. для общеобразоват. организаций : базовый и углубл. уровни и др. – М.: Просвещение, 2014. – 255, сс. 121-126.
Дополнительная литература:
Шарыгин И.Ф. Геометрия. 10–11 кл. : учеб. для общеобразоват. учреждений – М.: Дрофа, 2009. – 235, : ил., ISBN 978–5–358–05346–5, сс. 178-196.
Потоскуев Е.В., Звавич Л.И. Геометрия. 11кл.: учеб. Для классов с углубл. И профильным изучением математики общеобразоват. Учреждений – М.: Дрофа, 2004. – 368 с.: ил., ISBN 5–7107–8310–2, сс. 5-30.
Открытые электронные ресурсы:
Образовательный портал “Решу ЕГЭ”. https://mathb-ege.sdamgia.ru/test?theme=177
Теоретический материал для самостоятельного изучения
Шаром называется множество всех точек пространства, находящихся от данной точки на расстоянии, не больше данного R.
Радиусом шара называют всякий отрезок, соединяющий центр шара с точкой шаровой поверхности.
Отрезок, соединяющий две точки шаровой поверхности и проходящий через центр шара, называется диаметром шара.
Концы любого диаметра шара называются диаметрально противоположными точками шара. Отрезок, соединяющий две любые точки шаровой поверхности и не являющийся диаметром шара, называют хордой шара.
Сферическим поясом (шаровым поясом) называют часть сферы, заключенную между двумя параллельными плоскостями
Шаровым слоем называют часть шара, заключенную между двумя параллельными плоскостями
Сферическим сегментом называют каждую из двух частей, на которые делит сферу пересекающая ее плоскость.
Шаровым сегментом называется часть шара, отсекаемая от него какой-нибудь плоскостью.
Шаровым сектором называют фигуру, состоящую из всех отрезков, соединяющих точки сферического сегмента с центром сферы
Объем шара равен 
Объем шарового сегмента равен 
Объем шарового сектора равен 
Объем шарового слоя равен 
Площадь сферы равна S=4 πR2.
Примеры и разбор решения заданий тренировочного модуля
№1. Круговой сектор радиуса R с центральным углом 60 градусов вращается вокруг одного из радиусов, образующих этот угол. Найдите объем тела вращения.
Решение:
При вращении кругового сектора АОВ вокруг радиуса ОА получается тело вращения — шаровой сектор радиуса R=ОА и высотой сектора h=DA. Объем его вычисляется по формуле: V= (2/3)*πR²*h. Рассмотрим сечение этого сектора (смотри рисунок): в прямоугольном треугольнике ОВD (радиус круга ОА перпендикулярен хорде ВС) угол ВОD равен 60° (дано). Значит Тогда высота шарового сектора равна h=DA=OA-OD=R-R/2=R/2.
V=(2/3)*π*R²*R/2=(1/3)πR³.
№2. Найдите объем шарового сектора, если радиус шара равен 6 см, а высота конуса, образующего сектор, составляет треть диаметра шара.
Решение:
Шаровой сектор — это часть шара, ограниченная кривой поверхностью шарового сегмента и конической поверхностью, основанием которой служит основание сегмента, а вершиной — центр шара. Формула объема шарового сектора: V = (2/3)*πR²*h, где h — высота сегмента. В нашем случае R=H+h, где Н — высота конуса, а h- высота сегмента. Тогда h = R-H = 6-4 =2, так как Н = (1/3)*2*R (дано). Значит V = (2/3)*π*36*2 = 48π.
Ответ: объем шарового сектора равен 48π
№3.По разные стороны от центра шара проведены два параллельных сечения с площадью 


Решение: запишем формулу для вычисления объема шарового слоя.
Чтобы найти объём шарового слоя нам необходимо знать его высоту и радиусы двух его оснований.
По условию задачи нам дано расстояние между сечениями, как раз-таки это расстояние и есть высота данного шарового слоя, и она равна 
Теперь найдём чему равны радиусы оснований шарового слоя. Напомню, что сечением шара плоскостью является круг. Площадь круга вычисляется по формуле 


Подставим радиусы оснований и высоту шарового слоя в формулу его объёма. Посчитаем. Получаем, что объём данного шарового слоя равен 
На странице вы сможете рассчитать объем шарового сектора. Для этого мы подготовили калькулятор и формулу для расчета объема шарового сектора. Просто введите радиус шара и высоту сегмента и тут же получите результат.
Шаровый сектор — тело, получаемое вращением кругового сектора с углом, меньшим 90°, вокруг прямой, содержащей один из ограничивающих круговой сектор радиусов.
Формула объёма шарового сектора
{V= dfrac{2}{3}pi R^2 h}
R — радиус шара
h — высота шарового сегмента
Примеры задач на нахождение объема шарового сегмента
Задача 1
Найдите объем шарового сегмента, если радиус шара равен 8 см, а высота сегмента — 3см.
Решение
Подставим значения в формулу и получим результат.
V = dfrac{2}{3}pi R^2 h = dfrac{2}{cancel{3}}pi cdot 8^2 cdot cancel{3} = 128 pi : см^3 approx 402.12386 : см^3
Ответ: 128 pi : см^3 approx 402.12386 : см^3
Проверить результат удобно с помощью калькулятора .