Содержание:
Определение площади и объема:
В повседневной жизни нам довольно часто приходится иметь дело с определением таких величин, как площадь и объем. Представьте себе, что вам необходимо сделать ремонт в квартире (или доме): побелить стены и потолок, покрасить пол. Чтобы закупить необходимое количество материалов, нужно определить площадь поверхностей и объем краски.
Из уроков математики вам известно, как находить площадь некоторых фи-гур: квадрата, прямоугольника, параллелограмма.
|
Рис. 6.1. |
Рис. 6.2. |
Рис. 6.3 |
Площадь прямоугольника ABCD (рис. 6.1) вычисляется по формуле:
S = a · b, (6.1)
где a – ширина прямоугольника, b – высота.
Площадь параллелограмма ABCD (рис. 6.2) также находится по формуле 6.1. Площадь квадрата найти легко, поскольку его ширина и высота одинаковы:
S = a · a = a2 , (6.2)
Из рис. 6.1 видно, что площадь прямоугольного треугольника АBC можно найти по формуле:
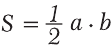
Проблема определения площади круга была решена еще в Древней Греции. Для этого нужно знать радиус круга и число «пи», приблизительное значение
которого π ≈ 3,14.
Площадь круга равняется
S = π · R2, (6.4) .
Значение числа 
Вычисление объема простых фигур
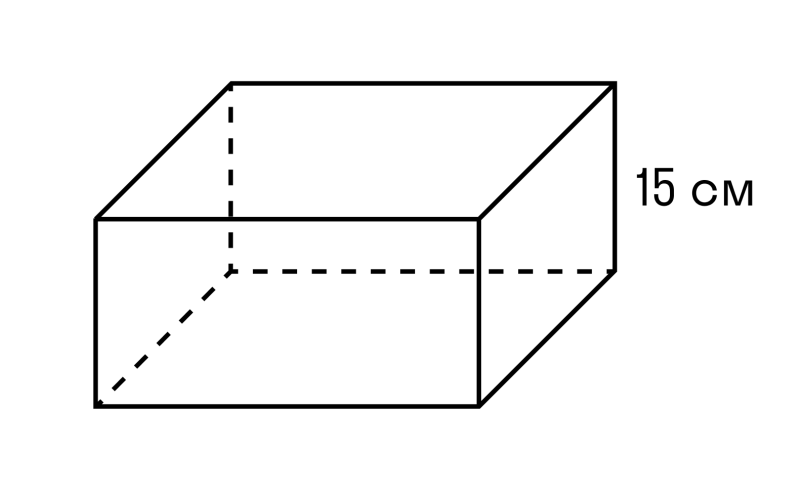
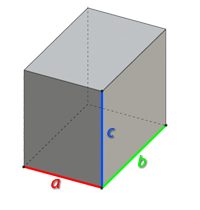
Каждое тело занимает определенный объем. Чем большую часть пространства занимает тело, тем больше его объем. Объем обозначают буквой V (от volume – объем). Чтобы найти объем прямоугольного бруска или ящика (математики называют эту геометрическую фигуру параллелепипедом) со сторона-ми a, b и h, надо их перемножить (рис. 6.4):
|
Рис. 6.4. |
Рис. 6.5. |
|
V = a · b · h (6.4)
Поскольку S = a · b,
где S – это площадь основания ящика, то формулу (6.4) можно переписать и так:
V = S · h (6.5)
У куба все ребра равны, потому его объем равняется:
V = a · a · a = a3 (6.6)
Объем цилиндра (рис. 6.5) с радиусом основания R и высотой h можно также определить по формуле (6.5), то есть:
V = S · h = πR2 · h (6.7)
Объем шара (рис. 6.6)
Единицы измерения объема
Поскольку длину сторон измеряют в единицах длины (метр, дециметр, сантиметр и т. д.), то единицы измерения объема – это единицы длины, возведенные в третью степень.
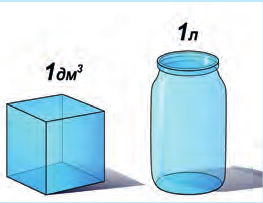
Куб с ребром 1 м имеет объем 1 м3 (один кубический метр). Один литр (1 л) по определению – это объем куба с ребром 1 дм (рис. 6.7), то есть 1 л = 1 дм3 (дециметр кубический). Один литр равен 1000 кубических сантиметров: 1 л = 1000 см3. Объем в один сантиметр кубический еще называют миллилитром, то есть тысячной частью литра (1 мл = 0,001 л).
Рис. 6.7. Один литр – это 1дм3
Напомним, что дециметр – это десятая часть метра, а сантиметр – сотая часть метра
Таблица 6.1
| 1 м3 = 1 000 л | 1 м3 = 1 000 000 см3 |
| 1 л = 1 дм3 | 1 л = 1000 см3 |
| 1 дм3 = 1 000 см3 | 1 л = 1 000 мл |
| 1 см3 = 1 мл | 1 мл = 0,001 л |
- Заказать решение задач по физике
Измерение объема тел неправильной формы
Прибор для измерения объема называют мензуркой, или мерным цилиндром (рис. 6.8). Мензурка – это прозрачный сосуд с нанесенными делениями, которые обозначают объем в миллилитрах. Дома у вас наверняка есть мерный стакан, то есть та же мензурка. Литровой или поллитровой банкой, или стаканом (250 мл) также можно пользоваться, если не нужна большая точность. С помощью мензурки можно определить объем жидкости и тела неправильной формы. Для этого в мензурку нужно налить воду и определить объем этой воды. Потом полностью погрузить тело в воду и запомнить новое значение объема. Разница измеренных значений равна объему тела.
Рис. 6.8. Деления мензурки определяют объем в миллилитрах (то есть в см3)
История:
 |
Существует легенда, согласно которой первым такой способ определения объема изобрел древнегреческий ученый Архимед. Произошло это во время размышлений над довольно сложной зада-чей, предложенной царем Гиероном. Идея решения возникла тогда, когда Архимед влез в ванну и заметил, что уровень воды поднялся. Ученый понял, что вытесненный объем воды как раз равен объему погруженного в нее тела. Восторженный Архимед выпрыгнул из ванны и выбежал на улицу с криком «Эврика! Эврика!», что в переводе с древнегреческого значит «На-шел! Нашел!». |
Итоги:
- Площадь тел правильной формы равна произведению основы на высоту и измеряется в квадратных единицах длины S = a · b.
- Объем тел правильной формы определяется как произведение площади основы на высоту и измеряется в кубических единицах V = S · h.
- Объем тел произвольной формы определяют с помощью мензурки
- Площадь круга определяют по формуле S = π · R2.
- Объем шара равен
.
- Связь физики с другими науками
- Макромир, мегамир и микромир в физике
- Пространство и время
- Что изучает механика в физике
- Единая физическая картина мира
- Физика и научно-технический прогресс
- Физические величины и их единицы измерения
- Точность измерений и погрешности
Калькулятор для расчета объема параллелепипеда
C помощью нашего Онлайн-калькулятора для расчета объема параллелепипеда Вы можете быстро и точно рассчитать объем прямоугольного параллелепипеда. Для того, чтобы вычислить объем прямоугольного параллелепипеда, введите значение ребер «a», «b», «c» и нажмите кнопку «Рассчитать». Также Вы можете указать точность полученного результата, т.е. количество знаков после запятой, до которого будет округлен рассчитанный объем параллелепипеда.
Задайте значение ребер параллелепипеда а, b, c и нажмите кнопку «Рассчитать»
Округлить результат до
знаков после запятой
Рассчитать
Прямоугольный параллелепипед – это многогранник, у которого все грани являются прямоугольниками.
Объем прямоугольного параллелепипеда вычисляется по следующей формуле:
,
где a, b, c – ребра параллелепипеда.
Данные задачи: L (длина взятого прямоугольного бруска) = 10 см; S (ширина бруска) = 5 см; h (высота) = 4 см.
Объем взятого прямоугольного бруска можно вычислить по формуле: V = L * S * h.
Вычисление: V = 10 * 5 * 4 = 200 см³.
Объем бруска в дм³: V = 200 * 10-3 дм³ = 0,2 дм³.
Объем бруска в м³: V = 200 * 10-6 м3 = 0,0002 м³.
Ответ: Объем взятого бруска равен 200 см³ или 0,2 дм³, или 0,0002 м³.
поделиться знаниями или
запомнить страничку
- Все категории
-
экономические
43,662 -
гуманитарные
33,654 -
юридические
17,917 -
школьный раздел
611,985 -
разное
16,906
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
Вот несколько наиболее эффективных способов расчета объема бревна. Пример алгоритма расчета кубатуры бруса.
Несколько способов вычисления кубатуры лесоматериалов
Древесина часто используется для строительства: избы, санузла, беседки и других построек. Но тогда, чтобы совершить покупку, изначально ориентируясь на реальное количество материалов, необходимо знать их объемы (кубатура). Как рассчитать объем бревна?
Традиционно ее измеряют в кубических метрах и все это называется кубатурой. Посмотрим, как правильно рассчитать. Существуют методы определения объемов круглого пиломатериала и других пиломатериалов, необходимых для покупки / продажи.
Формула массы через плотность и объем — одна из основных формул физики, изучаемая в контексте школьной программы седьмого класса. Она пригодится
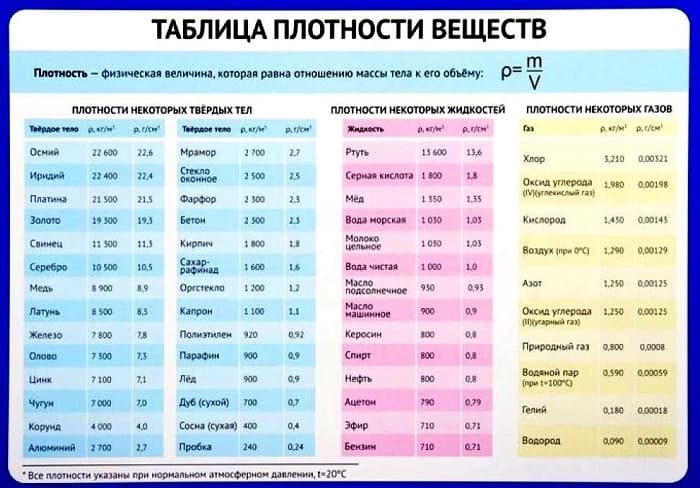
Таблица плотности некоторых веществ
Плотность многих веществ известна заранее и ее легко найти по соответствующей таблице.
При работе с ним важно обращать внимание на размер и не забывать, что все данные собираются в нормальных условиях: температура окружающей среды 20 градусов Цельсия, а также определенное давление, влажность и так далее.
Плотность других более редких веществ можно найти в Интернете.
Стоит запомнить хотя бы одно из значений плотности, так как оно часто встречается в задачах. Это плотность воды — 1000 кг / м3 или 1 г / см3.
Статьи
Расчет объема отдельных бревен
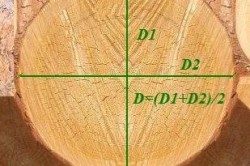
Рисунок 1. Измерение двух перпендикулярных диаметров в поперечном сечении стержня
Если кругляк имеет такую же длину, что и бревна, и такой же диаметр, то можно выборочно рассчитать объем 3 балок, уменьшить их до расчетного среднего значения и умножить на количество материала бревна. В этом случае расчеты производятся следующим образом:
- Выберите любые 3 луча.
- Измерьте их диаметр и длину. Для удобства расчета производите измерения в метрах.
- Вычислите кубическое пространство, занимаемое каждым из раундов, по формуле:
R — радиус, равный половине измеренного диаметра,
- Полученные значения 3 кубометров круглого леса будут близки друг к другу. Их нужно сложить и сумму разделить на 3. Итак, мы получаем среднее значение объема бревна.
- Далее умножаем полученное среднее значение на количество заготовок в машине или на складе.
Поскольку для строительства используются бревна одинакового диаметра и стандартной длины, этот метод широко используется для оценки объема строительных лесов.
Если форму бруска слегка придавить, его разрез будет не круглым, а слегка овальным. Как тогда определить значение диаметра? Для этого отмерьте размер 2-х перпендикулярных диаметров в сечении бруса — самого большого и самого маленького. Затем измеренные значения складываются и делятся на 2. Полученное значение будет средним диаметром, используемым в расчетах (рис. 1).
Как правильно найти объем параллелепипеда и не ошибиться? Формулы, наглядные примеры расчетов. Давайте просто поговорим о комплексе.
Задачи на самопроверку
Вы можете использовать онлайн-калькуляторы, когда вы уже обучены решать задачи и с закрытыми глазами можете рассчитать объем любого ящика. Давайте рассмотрим еще несколько примеров.
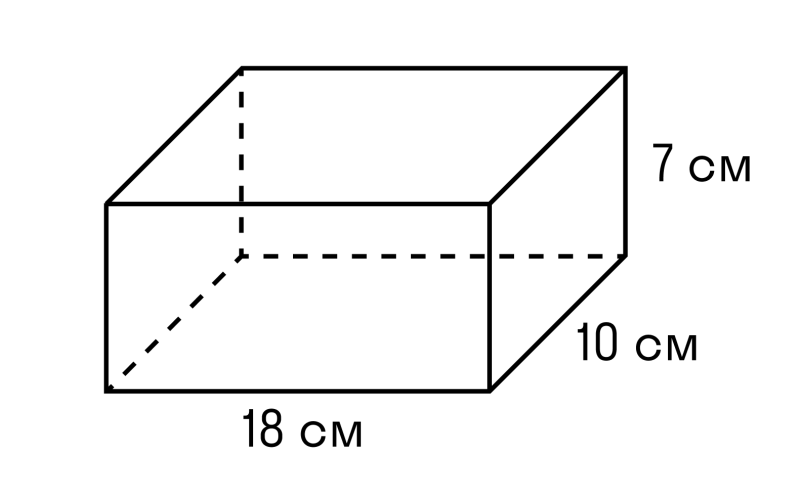
Задача 1. Найдите объем параллелепипеда со сторонами 18 см, 10 см, 7 см.
Формула для определения объема параллелепипеда:
Ответ: объем параллелепипеда 1260 см 3 .
Задача 2. Найдите площадь основания параллелепипеда, если его объем составляет 120 см 3, а высота — 15 см.
Сб = 120 см 3:15 см = 8 см 2 .
Ответ: Площадь основания параллелепипеда 8 см 2 .
Задача 3. Найдите общую площадь прямоугольного параллелепипеда, если длина основания 30 сантиметров, ширина 12 сантиметров и высота 5 сантиметров.
SP п. = 2 (30 × 12 + 30 × 5 + 12 × 5) = 2 × (360 + 150 + 60) = 2 × 570 = 1140 см 2 .
Ответ: общая площадь параллелепипеда 1140 см 2 .
Имейте под рукой все необходимые формулы, когда они вам понадобятся. Сохраните шпаргалку на свой гаджет или распечатайте и храните в учебнике.
Сколько бревен в кубе: онлайн калькулятор Эта операция имеет очень простую математическую схему. Объем любого прямоугольного объекта рассчитывается путем умножения его ширины на
Чтобы рассчитать кубатуру на дом и определить точное количество стропил, нужно выполнить несложные расчеты. Для этого нужна некоторая информация: объем пиломатериалов и объем производимой детали. Это необходимо для деления одной величины на другую. В таблице ниже показаны размеры наиболее распространенных секций. При этом длина материала составляет 6 метров.
Формула для расчета количества деревяшек в кубе 150 * 150 * 6000:
0,15 (м) * 0,15 (м) * 6 (м) = 0,135 кубических метров
1 м³ / 0,135 м³ = 7 штук в одном кубе.
Как перевести погонные метры в кубические?
Подсчет количества пиломатериалов в кубе продаваемого материала также может рассчитать обычный студент. Например, чтобы рассчитать количество пиломатериалов 150 * 150 в деревянном кубе, необходимо выполнить следующие действия. Размер края балки, указываемый в миллиметрах, квадратный. Итак, 100000 нужно разделить на полученное значение. В итоге получается, что в одном кубе 44,4 погонных метра материала. Количество шестиметровых лучей в кубе составит 7,4 штук. Внутри будет 11 четырехметровых балок.
Производители и продавцы пиломатериалов не всегда честны с покупателями. Сечение пиломатериалов часто занижается по сравнению с заявленным. Часто бывает, что проданный брус размером 150 × 200 на самом деле имеет сечение 140 × 190. Перед покупкой бруса необходимо проверить реальные параметры материала. Также важно узнать у поставщика формирование цены за куб материала.
Урожайность панели при распиловке круглого бруса в одних и тех же условиях может существенно различаться. Поэтому я выбрала критерии, от которых все зависит
Как зависит процент получения пилопродукции от технологии пиления
Процент выхода доски зависит не только от диаметра, сорта, дефектов (кривизны) и длины, но и от технологии распиловки древесины и типа оборудования.
Различают два типа режущей техники:
- Одинарная срезка, процент полезной урожайности приближается к 75 %;
- Групповая обрезка, в зависимости от других параметров, полезная урожайность может достигать 70 %.
А оборудование для резки может быть следующим:
- Ленточные пилорамы, на которых пиломатериалы производятся с минимальными коэффициентами расхода древесины;
- Шиномонтажные пилорамы при распиловке бревен производят пиломатериалы с завышенным расходом, так как толщина цепи намного больше, чем у лент… Работать с тонкой древесиной на таком оборудовании недостаточно удобно. Поэтому в основном его пилит диаметром 20 — 22 см;
- Кантовочные фрезерные линии. Этот тип оборудования имеет для человека преимущества и недостатки перед другими технологиями. Пила только разборную древесину;
- Оборудование для дисковых пил пил по индивидуальным пропилам — это большое преимущество для получаемых материалов, как по качеству, так и по количеству.
Источники
- https://viascio.ru/materialy/derevo/vychisleniya-kubatury-lesomaterialov
- https://sprint-olympic.ru/uroki/fizika/96675-formyla-massy-cherez-plotnost-i-obem-primery-vychislenii.html
- http://stroimdoma72.ru/info/articles/kak-pravilno-poschitat-obyem-brevna/
- https://skysmart.ru/articles/mathematic/obem-parallelepipeda
- https://o-terrasah.ru/skolko-brusa-v-kube
- https://andreynoak.ru/pervichnaya-derevoobrabotka/vyhod-pilomateriala-iz-kruglogo-lesa-po-sortam-i-v-zavisimosti-ot-diametra-breven/

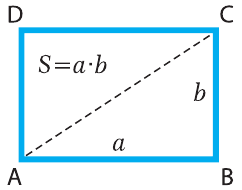
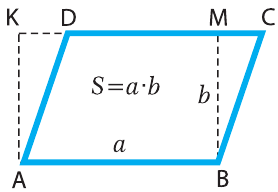
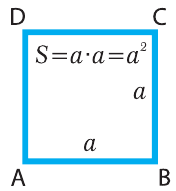
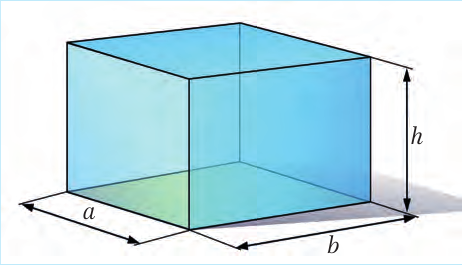
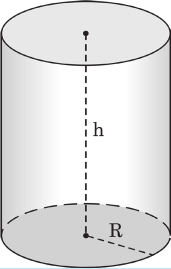
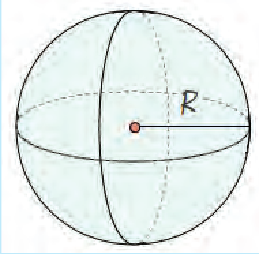 Рис. 6.6.
Рис. 6.6.