Как найти объем оболочки шара

From Wikipedia, the free encyclopedia

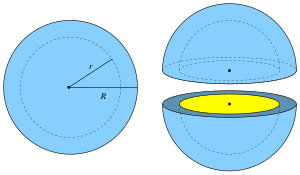
spherical shell, right: two halves

In geometry, a spherical shell is a generalization of an annulus to three dimensions. It is the region of a ball between two concentric spheres of differing radii.^[1]

Volume[edit]

The volume of a spherical shell is the difference between the enclosed volume of the outer sphere and the enclosed volume of the inner sphere:

${displaystyle V={frac {4}{3}}pi R^{3}-{frac {4}{3}}pi r^{3}}$

${displaystyle V={frac {4}{3}}pi left(R^{3}-r^{3}right)}$

${displaystyle V={frac {4}{3}}pi (R-r)left(R^{2}+Rr+r^{2}right)}$

where r is the radius of the inner sphere and R is the radius of the outer sphere.

Approximation[edit]

An approximation for the volume of a thin spherical shell is the surface area of the inner sphere multiplied by the thickness t of the shell:^[2]

${displaystyle Vapprox 4pi r^{2}t,}$

when t is very small compared to r ().

The total surface area of the spherical shell is $4pi r^{2}$ .

References[edit]

^ W., Weisstein, Eric. «Spherical Shell». mathworld.wolfram.com. Wolfram Research, Inc. Archived from the original on 2 August 2016. Retrieved 7 January 2017.
^ Znamenski, Andrey Varlamov, Lev Aslamazov; scientific editor, A.A. Abrikosov, Jr. ; translators, A.A. Abrikosov, Jr., J. Vydryg, & D. (2012). The wonders of physics (3rd ed.). Singapore: World Scientific. p. 78. ISBN 978-9814374156. Archived from the original on 20 December 2017. Retrieved 7 January 2017.

Источник

Объем полусферической оболочки с учетом толщины оболочки и большого радиуса полусферы Калькулятор

Search
Дом	математика ↺
математика	Геометрия ↺
Геометрия	3D геометрия ↺
3D геометрия	Полусферическая оболочка ↺
Полусферическая оболочка	Объем полусферической оболочки ↺

✖Радиусом большой полусферы полусферической оболочки называется отрезок прямой от центра до точки на криволинейной поверхности большой полусферы полусферической оболочки.ⓘ Большой радиус полусферы полусферической оболочки [r_{Large Hemisphere}]

+10%

-10%

✖Толщина полусферической оболочки — это радиальное расстояние между внешней и внутренней поверхностями полусферической оболочки.ⓘ Толщина оболочки полусферической оболочки [t_Shell]

+10%

-10%

✖Объем Полусферической оболочки – это мера трехмерного пространства, заключенного между всеми гранями Полусферической оболочки.ⓘ Объем полусферической оболочки с учетом толщины оболочки и большого радиуса полусферы [V]

⎘ копия

Объем полусферической оболочки с учетом толщины оболочки и большого радиуса полусферы Решение

ШАГ 0: Сводка предварительного расчета

ШАГ 1. Преобразование входов в базовый блок

Большой радиус полусферы полусферической оболочки: 12 метр —> 12 метр Конверсия не требуется
Толщина оболочки полусферической оболочки: 2 метр —> 2 метр Конверсия не требуется

ШАГ 2: Оцените формулу

ШАГ 3: Преобразуйте результат в единицу вывода

1524.71963454225 Кубический метр —> Конверсия не требуется

3 Объем полусферической оболочки Калькуляторы

Объем полусферической оболочки с учетом толщины оболочки и большого радиуса полусферы формула

Объем полусферической оболочки = 2/3*pi*(Большой радиус полусферы полусферической оболочки^3-(Большой радиус полусферы полусферической оболочки—Толщина оболочки полусферической оболочки)^3)

V = 2/3*pi*(r_{Large Hemisphere}^3-(r_{Large Hemisphere}—t_Shell)^3)

Что такое полусферическая оболочка?

Сферическая оболочка представляет собой обобщение кольца на три измерения. Это область шара между двумя концентрическими сферами разного радиуса. Полусферическая оболочка или полая полусфера состоит из двух полусфер разных размеров с одним и тем же центром и одной и той же плоскостью среза, где меньшая полусфера вычитается из большей.

Источник

Шаровым слоем называется часть шара, заключенная между двумя параллельными секущими плоскостями. Для
вычисления объема шарового слоя достаточно знать радиусы кругов, ограничивающих шаровой слой, и
расстояние между ними (высота шарового слоя). Объем вычисляется по формуле:

V = (π / 6) * h * (3R² + 3r² + h²)

где R, r — радиусы, h — высота.

Цифр после
запятой:

Результат в:

Пример. Требуется найти объём шарового слоя зная что радиусы R = 3 см, r = 6 см,
высота h = 4 см. Подставим в формулу и получим: V = (3,14 / 6) * 4 * (3 * 3² + 3 * 6² + 4²) = 316 см³.

Примечательно, что для вычисления этого объема не требуется радиус самого шара. Требуются только
радиусы ограничивающих его кругов. Если секущие плоскости отодвинуть к полюсам шара, то высота h
станет равна диаметру шара, а радиусы кругов примут нулевые значения: R=0, r=0. Тогда формула примет
вид: V = π / 6 D³ = (4π / 3) * Rшара³. Это формула для вычисления объема
шара. Максимальный объем шарового слоя равен объему шара.

Актуально вычисление шарового слоя при устройстве сферических резервуаров, применяемых в химической
промышленности. Сферическая емкость применяется в тех случаях, когда давление в ней высокое.
Резервуар может иметь вид полной сферы или шарового слоя. Если в шаровом резервуаре находится
жидкость, заполняющая только часть объема, то по положению ее уровня можно определить высоту
шарового слоя и радиус ограничивающего круга, а потом посчитать объем жидкости. Сферические сосуды
используются и в быту. Примером может служить аквариум, выполненный в виде усеченного шара (шарового
слоя). Расчет его объема нужен для правильного оборудования среды обитания для аквариумных жителей.
Части конструкций в виде шарового слоя встречаются в машиностроении, архитектуре, столярном деле.
Вычисление объемов – необходимая часть конструкторской разработки.

Источник

Шаровой слой, как геометрическое тело, образован сечением сферы двумя параллельными плоскостями. Для того чтобы рассчитать объем шарового слоя, следует представить его в виде разности двух шаровых сегментов – первый шаровой сегмент образуется отсечением его от сферы первой плоскостью, а вторая плоскость отсекает второй шаровой сегмент от первого. Таким образом, приведя алгебраически через подобие окружностей, лежащих в основаниях шарового слоя, соотношение высот, можно вывести формулу для нахождения объема шарового слоя:
V_{шар.слоя}=V_{шар.сег.1}-V_{шар.сег.2}

Источник

В данной публикации мы рассмотрим формулы, с помощью которых можно вычислить объем шарового слоя (среза шара), а также пример решения задачи для демонстрации их практического применения.

Определение шарового слоя
Формула для нахождения объема шарового слоя
Пример задачи

Определение шарового слоя

Шаровый слой (или срез шара) – это часть шара, оставшаяся между двумя пересекающими его параллельными плоскостями. На рисунке ниже окрашен в желтый цвет.

R – радиус шара;
r₁ – радиус первого основания среза;
r₂ – радиус второго основания среза;
h – высота шарового слоя; перпендикуляр от центра первого основания до центра второго.

Формула для нахождения объема шарового слоя

Чтобы найти объем шарового слоя (среза шара), необходимо знать его высоту, а также радиусы двух его оснований.

Эта же формула может быть представлена слегка в другом виде:

Примечания:

если вместо радиусов оснований (r₁ и r₂) известны их диаметры (d₁ и d₂), последние нужно поделить на 2 для получения соответствующих им радиусов.
число π обычно округляется до 3,14.

Пример задачи

Найдите объем шарового слоя, если радиусы его оснований равны 3,4 см и 5,2 см, а высота составляет 2 см.

Решение

Все что нам нужно сделать в данном случае – это подставить известные значения в одну из формул, приведенных выше (в качестве примера выберем вторую):

Источник

Volume[edit]

Approximation[edit]

See also[edit]

References[edit]

Объем полусферической оболочки с учетом толщины оболочки и большого радиуса полусферы Калькулятор

Объем полусферической оболочки с учетом толщины оболочки и большого радиуса полусферы Решение

3 Объем полусферической оболочки Калькуляторы

Объем полусферической оболочки с учетом толщины оболочки и большого радиуса полусферы формула

Что такое полусферическая оболочка?

Определение шарового слоя

Формула для нахождения объема шарового слоя

Пример задачи

Не пропустите также: