Как найти объем куба вписанного в сферу - Avtoru.top

Факт 1.
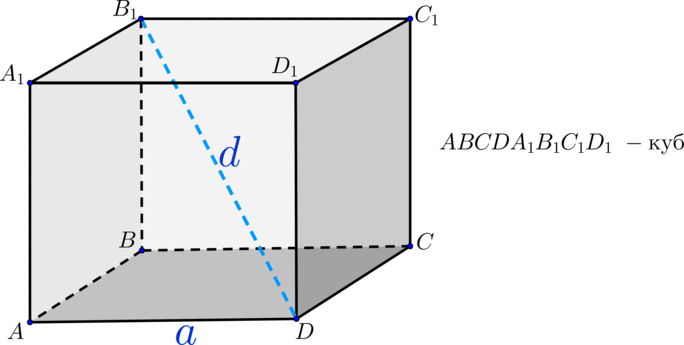
(bullet) Куб – это прямоугольный параллелепипед, все грани которого – равные квадраты.
(bullet) Следовательно:

— ({color{red}{{small{объем куба}}}}) ищется по следующей формуле (где (a) – ребро куба): [{color{red}{{large{V=a^3}}}}] — ({color{red}{{small{диагональ куба}}}}) [{color{red}{{large{d^{,2}=3a^2}}}}] — ({color{red}{{small{площадь поверхности куба}}}}) равна сумме площадей шести одинаковых квадратов, т.е. [{color{red}{{large{S_{text{пов.куб}}=6a^2}}}}]

Факт 2.
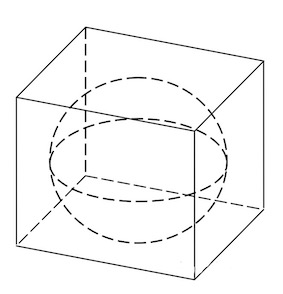
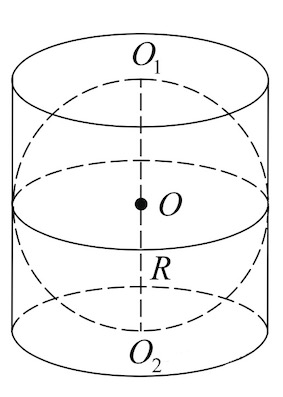
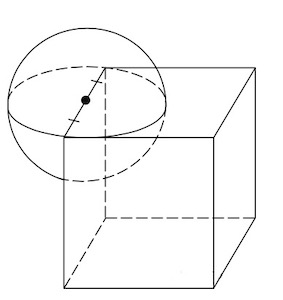
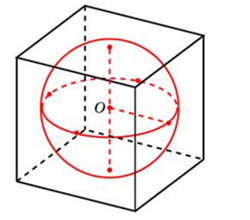
(bullet) Если сфера вписана в куб (то есть касается всех его граней), то ее радиус равен (0,5a), где (a) – ребро куба.
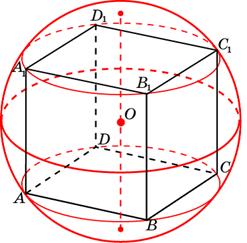
(bullet) Если сфера описана около куба (то есть все вершины куба лежат на сфере), то ее радиус равен (0,5d), где (d) – диагональ куба.
(bullet) Центр сферы, вписанной в куб или описанной около куба, лежит в точке пересечения диагоналей куба.

Источник

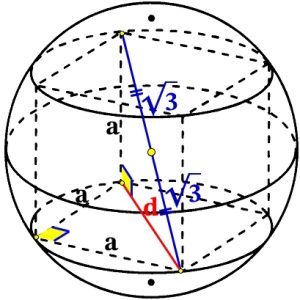
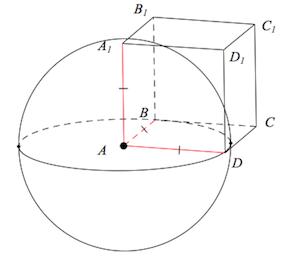
Куб вписан в шар радиуса √3. Найдите объем куба.

Источник: mathege

Решение:

Диаметр шара является диагональю куба, найдём её:

D = r + r = √3 + √3 = 2√3

Из двух прямоугольных треугольников, по теореме Пифагора, выразим и найдём сторону куба а:

d² = a² + a²
d² = 2a²
d = √2·a

Тогда:

(2√3)² = а² + d²
12 = а² + (√2·a)²
12 = а² + 2·a²
12 = 3·a²
a² = 12/3
a² = 4
a = √4 = 2

Найдём объём куба:

V = a³ = 2³ = 8

Ответ: 8.

Есть три секунды времени? Для меня важно твоё мнение!

Насколько понятно решение?

Средняя оценка: 3.1 / 5. Количество оценок: 12

Оценок пока нет. Поставь оценку первым.

Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️

Вступай в группу vk.com 😉

Расскажи, что не так? Я исправлю в ближайшее время!

В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.

Источник

Обновлено: 15.11.2022

Задание

Куб описан около сферы радиусом 9,5. Найдите объём куба.

Решение

Так как у куба все ребра одинаковой длины, то объем куба равен длине ребра в кубе: V=h³.
Длина ребра равна диаметру (двум радиусам) сферы, так как куб описан около данной сферы, то есть длина ребра: 9,5*2=19.
Подставим длину ребра в формулу объема куба и найдем, соответственно, сам объем:

V = 19³ = 6859 – объем куба.

Ответ: 6859

Источник

Задача 1. Объем прямоугольного параллелепипеда, описанного около сферы, равен Найдите радиус сферы.

Решение: + показать

Задача 2. В куб вписан шар радиуса Найдите объем куба.

Решение: + показать

Задача 3. Шар, объём которого равен вписан в куб. Найдите объём куба.

Решение: + показать

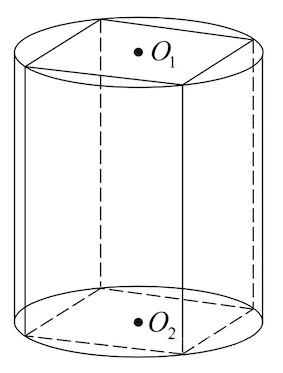
Задача 4. Прямоугольный параллелепипед описан около цилиндра, радиус основания которого равен Объем параллелепипеда равен Найдите высоту цилиндра.

Решение: + показать

Задача 5. Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого равны Найдите объем параллелепипеда.

Решение: + показать

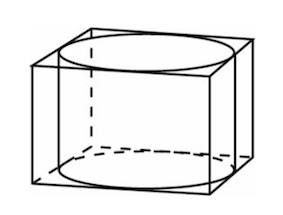
Задача 6. Правильная четырехугольная призма описана около цилиндра, радиус основания и высота которого равны Найдите площадь боковой поверхности призмы.

Решение: + показать

Задача 7. В основании прямой призмы лежит квадрат со стороной . Боковые ребра равны $frac{5}{pi}.$ Найдите объем цилиндра, описанного около этой призмы.

Решение: + показать

Задача 8. Около шара описан цилиндр, площадь поверхности которого равна Найдите площадь поверхности шара.

Решение: + показать

Задача 9. Цилиндр описан около шара. Объем цилиндра равен Найдите объем шара.

Решение: + показать

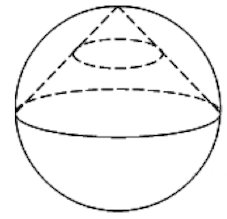
Задача 10. Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объем шара равен Найдите объем конуса.

Решение: + показать

Задача 11. Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объем конуса равен Найдите объем шара.

Решение: + показать

Задача 12. Середина ребра куба со стороной является центром шара радиуса Найдите площадь части поверхности шара, лежащей внутри куба. В ответе запишите $frac{S}{pi}.$

Решение: + показать

Задача 13. Вершина куба со стороной является центром сферы, проходящей через точку . Найдите площадь части сферы, содержащейся внутри куба. В ответе запишите величину $frac{S}{pi}$ .

Решение: + показать

Задача 14. Цилиндр и конус имеют общие основание и высоту. Найдите объем конуса, если объем цилиндра равен

Решение: + показать

Задача 15. Цилиндр и конус имеют общие основание и высоту. Высота цилиндра равна радиусу основания. Площадь боковой поверхности цилиндра равна Найдите площадь боковой поверхности конуса.

Решение: + показать

Задача 16. Конус описан около правильной четырехугольной пирамиды со стороной основания и высотой Найдите его объем, деленный на .

Решение: + показать

Задача 17. Во сколько раз объем конуса, описанного около правильной четырехугольной пирамиды, больше объема конуса, вписанного в эту пирамиду?

Решение: + показать

Задача 18. Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объем шара равен Найдите объем конуса.

Решение: + показать

Задача 19. Около конуса описана сфера (сфера содержит окружность основания конуса и его вершину). Центр сферы находится в центре основания конуса. Радиус сферы равен Найдите образующую конуса.

Решение: + показать

Задача 20. В основании прямой призмы лежит прямоугольный треугольник с катетами и Боковые ребра равны $frac{6}{pi}$ . Найдите объем цилиндра, описанного около этой призмы.

Решение: + показать

Задача 21. Найдите площадь боковой поверхности правильной треугольной призмы, описанной около цилиндра, радиус основания которого равен а высота равна

Решение: + показать

Задача 22. Найдите площадь боковой поверхности правильной треугольной призмы, вписанной в цилиндр, радиус основания которого равен а высота равна

Решение: + показать

Задача 23. Цилиндр и конус имеют общее основание и общую высоту. Вычислите объем цилиндра, если объем конуса равен

Решение: + показать

Задача 24. Найдите площадь боковой поверхности правильной треугольной призмы, описанной около цилиндра, радиус основания которого равен , а высота равна

Решение: + показать

Задача 25. Найдите площадь боковой поверхности правильной шестиугольной призмы, описанной около цилиндра, радиус основания которого равен , а высота равна

Решение: + показать

Задача 26. Около куба с ребром описан шар. Найдите объем этого шара, деленный на

Решение: + показать

Задача 27. Куб вписан в шар радиуса Найдите объем куба.

Решение: + показать

Вы можете пройти тест “Комбинация тел”

Источник

Получаем, что диагональ куба есть диаметр шара, значит диагональ куба равен 2sqrt(3) (sqrt — означает корень). Если сторона куба А, то A*sqrt(3)=2sqrt(3), значит сторона куба 2. Отсюда обьем равен 8