Объём конуса
- Главная
- /
- Математика
- /
- Геометрия
- /
- Объём конуса
Для того чтобы посчитать объём конуса, просто воспользуйтесь нашим удобным онлайн калькулятором:
Онлайн калькулятор
Через площадь основания и высоту
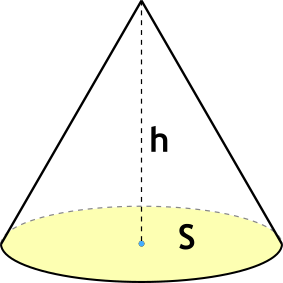
Площадь основания Sосн =
Высота h =
V =
0
Округление ответа:
Через радиус и другие параметры
=
=
V =
0
Округление числа π: Округление ответа:
Просто введите данные, и получите ответ.
Теория
Объём конуса через площадь основания и высоту
Чему равен объём конуса V, если площадь его основания Sосн, а высота h:
Формула
V = ⅓ ⋅ Sосн ⋅ h
Пример
Для примера посчитаем, чему равен объём конуса, у которого площадь основания Sосн = 3 см², а высота h = 5 см :
V = ⅓ ⋅ 3 ⋅ 5 = 15⁄3 = 5 см³
Объём конуса через образующую и радиус
Чему равен объём конуса V, если его образующая l, радиус основания r?
Формула
V = ⅓ ⋅ π ⋅ r² ⋅ √l² — r²
через диаметр:
V = ⅓ ⋅ π ⋅ (d/2)² ⋅ √l² — (d/2)²
Пример
Для примера посчитаем, чему равен объём конуса, у которого образующая l = 5 см, а радиус основания r = 2 см:
V = ⅓ ⋅ 3.14 ⋅ 2² ⋅ √5² — 2² = ⅓ ⋅ 12.56 ⋅ √21 ≈ 4.19 ⋅ 4.58 ≈ 19.19 см³
Объём конуса через радиус и высоту
Чему равен объём конуса V, если радиус его основания r, а высота h?
Формула
V = ⅓ ⋅ π ⋅ r² ⋅ h
через диаметр:
V = ⅓ ⋅ π ⋅ (d/2)² ⋅ h
Пример
Для примера посчитаем объём конуса, у которого высота h = 6 см, а радиус основания r = 3 см:
V = ⅓ ⋅ 3.14 ⋅ 3² ⋅ 6 = 169.56/3 = 56.52 см³
Объём конуса через угол раствора (α) и радиус
Чему равен объём конуса V, если угол раствора α, а радиус основания r?
Формула
V = ⅓ ⋅ π ⋅ r³/tg (α/2)
Пример
Для примера посчитаем объём конуса, имеющего угол раствора α = 30° и радиус основания r = 2 см:
V = ⅓ ⋅ 3.14 ⋅ 2³/tg(30/2) ≈ 1,0467 ⋅ 8 / 0.2679 ≈ 31.25 см³
Объём конуса через угол β и радиус
Чему равен объём конуса V, если известны угол β и радиус основания r?
Формула
V = ⅓ ⋅ π ⋅ r³/tg β
Пример
Для примера посчитаем объём конуса, имеющего угол β = 20° и радиус основания r = 3 см:
V = ⅓ ⋅ 3.14 ⋅ 3³/tg 20 ≈ 1,0467 ⋅ 27 / 0.36397 ≈ 77.64 см³
Объём конуса через угол γ и радиус
Чему равен объём конуса V, если известны угол γ и радиус основания r?
Формула
V = ⅓ ⋅ π ⋅ r³ ⋅ tg γ
Пример
Для примера посчитаем объём конуса, имеющего угол γ = 45° и радиус основания r = 2 см:
V = ⅓ ⋅ 3.14 ⋅ 2³ ⋅ tg 45 ≈ 1,0467 ⋅ 8 ⋅ 1 ≈ 8.37 см³
См. также
Поскольку объем конуса равен произведению высоты на треть площади основания конуса, то, зная объем и высоту, легко найти площадь круга в основании, а затем радиус и диаметр конуса.
S_(осн.)=3V/h
r=√(S_(осн.)/π)=√(3V/πh)
d=2r=2√(3V/πh)
Чтобы найти образующую конуса через объем и высоту, необходимо построить прямоугольный треугольник с образующей в виде гипотенузы и радиусом и высотой как катетами треугольника. Тогда образующая будет равна квадратному корню из суммы квадратов высоты и радиуса по теореме Пифагора, а угол между основанием и образующей можно будет найти через тангенс отношения высоты к радиусу. (рис.40.1)
l=√(h^2+r^2 )=√(h^2+3V/πh)
tanβ=h/r=h/√(3V/πh)=h√(πh/3V)
Угол раствора конуса можно найти, зная угол между образующей и основанием, и соединив их в равнобедренном треугольнике, где боковой стороной будет образующая, а основанием треугольника – диаметр конуса. (рис.40.2)
α=180°-2β
Площадь боковой поверхности конуса равна произведению радиуса на образующую и число π, а площадь полной поверхности представляет собой сумму площади боковой поверхности и площади основания, которую можно найти через объем.
S_(б.п.)=πrl=π√(3V/πh (h^2+3V/πh) )
S_(п.п.)=S_(б.п.)+S_(осн.)=π√(3V/πh (h^2+3V/πh) )+3V/h
Радиусы вписанной и описанной около конуса сфер можно найти из отношений, связывающих не только высоту конуса, которая известна, но и образующую, а также радиус основания конуса. (рис.40.3,40.4)
r_1=hr/(l+r)=(h√(3V/πh))/(√(h^2+3V/πh)+√(3V/πh))=(h√3V)/(√(πh^3+3V)+√3V)
R=(h^2+3V/πh)/2h
Конус – это тело в пространстве, образованное путем вращения прямоугольного треугольника вокруг одного из его катетов.
Онлайн-калькулятор объема конуса
Конус – это тело, образованное совокупностью всех лучей, исходящих из точки пространства и пересекающих плоскость.
Точка, из которой лучи исходят, получила название вершины конуса. В случае, когда основанием конуса является многоугольник, он превращается в пирамиду.
Рассмотрим некоторые важные понятия.
Образующей конуса называется отрезок, который соединяет любую точку границы основания конуса, с его вершиной.
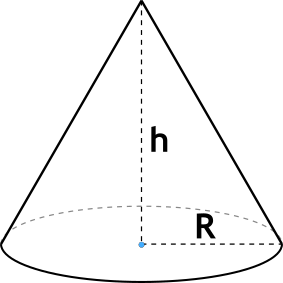
Высотой конуса является перпендикуляр, который опущен из вершины к основанию тела.
Конус бывает нескольких типов:
Прямой, если его основание – одна из таких фигур, как эллипс или круг. Обязательным условием является проецирование вершины конуса в центр основания.
Косой – у него центр фигуры, которая находится в основании, не совпадает с проекцией вершины на это самое основание.
Круговой – отталкиваясь от названия, понятно, что в его основании лежит круг.
Усеченный – область конуса, лежащая между основанием и сечением плоскости, которая параллельна основанию и пересекает данный конус.
Формула объема прямого конуса
Объем прямого конуса можно рассчитать по следующей формуле:
V=13⋅Sосн⋅hV=frac{1}{3}cdot S_{text{осн}}cdot h
где SоснS_{text{осн}} – площадь основания конуса;
hh – высота конуса.
Рассмотрим несколько примеров.
Найдите объем конуса, если его образующая ll равна 5см5text {см}, а радиус основания RR, которым является круг, равен 3 см3text{ см}.
Решение
l=5l=5
R=3R=3
Сперва найдем высоту конуса hh. Включим его в прямоугольный треугольник, гипотенузой которого является образующая. По теореме Пифагора:
l2=h2+R2l^2=h^2+R^2
Отсюда, hh:
h=l2−R2h=sqrt{l^2-R^2}
h=52−32h=sqrt{5^2-3^2}
h=25−9h=sqrt{25-9}
h=16h=sqrt{16}
h=4h=4
Затем находим площадь основания конуса. Это площадь круга радиуса RR:
Sосн=π⋅R2=π⋅32≈28.26S_{text{осн}}=picdot R^2=picdot3^2approx28.26
Последние вычисления — нахождение объема конуса по формуле:
V=13⋅Sосн⋅h≈13⋅28.26⋅4≈37.68 см3V=frac{1}{3}cdot S_{text{осн}}cdot happroxfrac{1}{3}cdot 28.26cdot 4approx37.68text{ см}^3
Ответ: 37.68 см3.37.68text{ см}^3.
Известен диаметр круга DD лежащего в основании конуса, равен он 8 см8text{ см}. Высота конуса равна 9 см9text{ см}. Найдите его объем.
Решение
D=8D=8
h=9h=9
Найдем радиус RR круга через его диаметр:
R=12⋅D=82=4R=frac{1}{2}cdot D=frac{8}{2}=4
Площадь этого круга и есть основание нашего конуса:
Sосн=π⋅R2=π⋅42≈50.24S_{text{осн}}=picdot R^2=picdot4^2approx50.24
Сам объем равен:
V=13⋅Sосн⋅h≈13⋅50.24⋅9≈150.72 см3V=frac{1}{3}cdot S_{text{осн}}cdot happroxfrac{1}{3}cdot 50.24cdot 9approx150.72text{ см}^3
Ответ: 150.72 см3.150.72text{ см}^3.
Вам нужно решить задачу по алгебре? Наши эксперты помогут вам!
Тест на тему “Объем конуса”

{V=dfrac {1}{3} pi r^2 h}
Конус — это трехмерная фигура, в основании которой лежит круг. Чтобы найти объем конуса достаточно знать два параметра — высоту (h) и радиус основания (r).
Содержание:
- калькулятор объема конуса
- формула объема конуса через высоту и радиус
- формула объема конуса через площадь основания и высоту
- формула объёма усеченного конуса
- примеры задач
Если мы сравним формулу объема конуса с формулой объема цилиндра, то мы увидим, что объем конуса в 3 раза меньше объема цилиндра с той же высотой и радиусом основания.
Наш калькулятор может рассчитать объем конуса через радиус основания и высоту, площадь основания и высоту, а также объем усеченного конуса через его высоту и радиусы нижнего и верхнего оснований.
Кроме того объем конуса можено найти, подставив значения в формулы, приведенные ниже.
Формула объёма конуса через радиус и высоту
{V=frac {1}{3} pi r^2 h}
r — радиус основания конуса,
h — высота конуса
Формула объёма конуса через площадь основания и высоту
{V=frac {1}{3} S h}
S — площадь основания конуса,
h — высота конуса
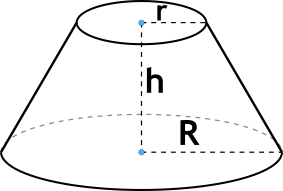
Формула объёма усеченного конуса
{V=frac {1}{3} pi h(r^2 + r R + R^2)}
h — высота усеченного конуса,
r — радиус меньшего основания усеченного конуса,
R — радиус большего основания усеченного конуса.
Примеры задач на нахождение объема конуса
Задача 1
Найдем объем конуса, высота которого 30см, а радиус основания 20см.
Решение
Подставим эти значения в формулу и произведем расчет:
V=dfrac {1}{3} pi r^2 h = dfrac {1}{3} cdot pi cdot 20^2 cdot 30 = dfrac {1}{3} cdot pi cdot 12000 = 400 pi : см^3 approx 12 566,37 : см^3
Ответ: {400 pi : см^3 approx 12 566,37 : см^3}
Проверить результат можно с помощью калькулятора .
Задача 2
Найдем объем конуса с высотой 3 см и диаметром основания 8 см².
Решение
Подставим эти значения в формулу и произведем расчет:
V=dfrac {1}{3} S h = dfrac {1}{3} cdot 8 cdot 3 = dfrac {1}{3} cdot 24 = 8 : см^3
Ответ: 8 см³
Воспользуемся калькулятором для проверки результата.
Задача 3
Найдите объем усеченного конуса радиусы оснований которого равны 1 см и 2 см, а высота равна 3 см.
Решение
Подставим высоту и радиусы оснований в формулу и произведем расчет:
V=dfrac {1}{3} pi h(r^2 + r R + R^2) = dfrac {1}{3} pi cdot 3 cdot (1^2 + 1 cdot 2 + 2^2) = dfrac {1}{3} pi cdot 3 cdot (1 + 2 + 4) = dfrac {1}{3} pi cdot 3 cdot 7 = dfrac {1}{3} pi cdot 21 = 7 pi : см^3 approx 21,99115 : см^3
Ответ: {7 pi : см^3 approx 21,99115 : см^3}
Проверим полученный ответ.
Конус – это геометрическая фигура, полученная вращением прямоугольного треугольника вокруг одного из катетов. У каждого конуса есть основание и боковая поверхность.
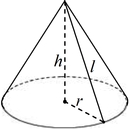
Любой конус характеризуется высотой h (осевой линией), радиусом r и образующей l (см. рисунок). Именно эти характеристики используются в формулах конуса при вычислении объема, площади поверхности и площади боковой поверхности.
Высота конуса (осевая линия) – это перпендикуляр, проведенный из вершины конуса к основанию.
Радиус конуса – это радиус его основания.
Образующая конуса – это отрезок, который соединяет вершину конуса с любой точкой, лежащей на линии окружности основания.
Формула образующей конуса
Образующую конуса можно найти, зная ее высоту H и радиус R:
L = √H2 + R2
Формула площади боковой поверхности конуса
Площадь боковой поверхности конуса можно получить, зная его радиус R и образующую L:
Sбок.пов = πRL
Формула площади основания конуса
Площадь основания конуса можно вычислить по его радиусу R:
Sосн = πR2
Формула площади конуса
Площадь поверхности конуса можно получить, сложив площадь боковой поверхности и площадь основания конуса:
S = Sбок.пов + Sосн = πRL + πR2
Формула объема конуса
Объем конуса можно вычислить, зная его высоту H и площадь основания:
V = 1/3 ⋅ Sосн ⋅ H = 1/3πR2H