Как найти объем конуса вписанного в куб - Avtoru.top

Пользуйтесь нашим приложением

Мы используем файлы cookie. Пользуясь сайтом, вы принимаете условия нашего соглашения. Принять Детальнее

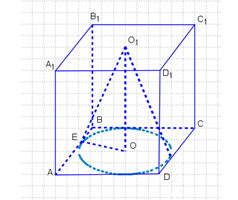
Объём куба найдем по формуле:
$V= a^{3}$ , где a = AD = DD1 — ребро куба.
OO1 = DD1 = 10 см.
$V= 10^{3} =1000$
Объем конуса найдем по формуле:
$V= frac{1}{3} pi R^{2} H$ , где R — радиус основания конуса, а H — высота конуса, которая равна боковому ребру куба, то есть H = DD1 = 10.
Радиус основания конуса, вписанного в куб, равен:
$R= frac{a}{2}$ , где a — ребро куба.
$R= frac{10}{2}=5$
Найдем объем конуса:
$V= frac{1}{3} pi R^{2} H= frac{1}{3}*25*10* pi = frac{250}{3} pi$
Ответ: 1000 и $frac{250}{3} pi$

Источник

Найдите обьем : б)конуса , вписанного в куб обьемом 216м3.

Причем вершиной конуса служит центр верхней грани куба.

На этой странице находится ответ на вопрос Найдите обьем : б)конуса , вписанного в куб обьемом 216м3?, из категории
Математика, соответствующий программе для 10 — 11 классов. Чтобы посмотреть
другие ответы воспользуйтесь «умным поиском»: с помощью ключевых слов
подберите похожие вопросы и ответы в категории Математика. Ответ, полностью
соответствующий критериям вашего поиска, можно найти с помощью простого
интерфейса: нажмите кнопку вверху страницы и сформулируйте вопрос иначе.
Обратите внимание на варианты ответов других пользователей, которые можно не
только просмотреть, но и прокомментировать.

Источник

1 ответ:

Читайте также

1) не факт. если треугольник тупоугольный, то серединные перпендикуляры пересекаются вне треугольника. А в прямоугольном прямо на гипотенузе.
2)да
3) нет (центр вписанной окружности — это точка пересечения биссектрис)
4)не факт ( в параллелограмме сумма углов = 360° , а не в каждый параллелограмм можно вписать окружность)

Решение во вложении……………………….

7) 1 <К= 120°
10 см
Голосуй за лучший ответ ^^

Площадь полной поверхности цилиндра в два раза больше площади его боковой поверхности. Найдите объем цилиндра, если его высота равна 2 см
1) 24П
2) 8П

3) 12П

4) 20П

конечно-2 !!!!!!!!!!

Из того, что AC и BD перпендикулярны к прямой CD следует, что треугольники ACD и BDC прямоугольные и равны (по катетам AD=BC и гипотенузе — их общая сторона CD).

Источник

Чтобы найти объем конуса необходимо произвести дополнительные построения.

Построим вписанную в конус правильную n-угольную пирамиду и опишем вокруг данного конуса правильную n-угольную пирамиду.
Вписанная пирамида содержится в конусе. Из этого следует, что ее объем не больше объема конуса.
Описанная пирамида содержит конус, а это значит, что ее объем не меньше объема конуса.

Впишем в основание вписанной пирамиды окружность.
Если радиус вписанного правильного n-угольника равен R, то радиус вписанной в него окружности будет равен:
$R_vpokr=R*cos{{pi}/n}$

Объем вписанной пирамиды вычисляется по формуле:

где S – основание пирамиды.
Площадь данного круга вычисляется по формуле: $S={pi}*(R{cos{{pi}/n}})^2={pi}R^2{cos^2{{pi}/n}}$
Площадь основания вписанной пирамиды не меньше площади круга, содержащегося в ней
Поэтому утверждение, что объем вписанной в конус пирамиды не меньше ${1/3}{pi}R^2H{cos^2{{pi}/n}}$ верно.
А следовательно, мы может утверждать, что объем конуса, содержащий эту пирамиду будет больше или равен ${1/3}{pi}R^2H{cos^2{{pi}/n}}$
V≥ ${1/3}{pi}R^2Hcos^2{{pi}/n}$

Теперь опишем окружность вокруг основания описанной вокруг конуса пирамиды.
Радиус этой окружности будет равен: $R_{op.okr}= R/ {cos { {pi}/n}}$

Площадь данного круга вычисляется по формуле: $S={pi}(R/{cos{{pi}/n}})^2$
Основание описанной пирамиды содержится в круге описанном вокруг него. Поэтому площадь основания пирамиды не больше ${pi}{{R^2}/{cos^2{{pi}/n}}}$
Поэтому утверждение,что объем описанной пирамиды не больше ${1/3}*{{{pi}HR^2}/{cos^2{{pi}/n}}}$ верно.
А следовательно, мы может утверждать, что объем конуса, содержащий в эту пирамиду будет меньше или равен ${1/3}{{{pi}HR^2}/{cos^2{{pi}/n}}}$
$V<={1/3}{pi}HR^2$
Два полученных неравенства равны при любом n. Если то
Тогда из первого неравенства следует, что V≥ ${1/3}{pi}HR^2$
Из второго неравенства $V<={1/3}{pi}HR^2$

Отсюда следует, что

$V={1/3}{pi}HR^2$

Объем конуса равен одной трети произведения радиуса на высоту.

Пример расчета объема конуса
Найти объем конуса, если его радиус основания равен 3 см, а образующая 5 см.
Объем конуса вычисляется по формуле:
$V={1/3}{pi}HR^2$
Для того, чтобы воспользоваться данной формулой необходимо найти высоту конуса. Образующая конуса, его высота и радиус основания образуют прямоугольный треугольник. Воспользовавшись теоремой Пифагора имеем:

Отсюда:
$H=sqrt{L^2-R^2}=sqrt{5^2-3^2}=sqrt{16}=4$
Подставим значение радиуса и высоты в формулу объема конуса.
Имеем:
$V={1/3}{pi}4*3^2=12{pi}$

Источник

Не пропустите также: