Как найти объем конуса когда известна образующая - Avtoru.top

Определение конуса

Конус – это тело в пространстве, образованное путем вращения прямоугольного треугольника вокруг одного из его катетов.

Онлайн-калькулятор объема конуса

Общее определение конуса

Конус – это тело, образованное совокупностью всех лучей, исходящих из точки пространства и пересекающих плоскость.

Точка, из которой лучи исходят, получила название вершины конуса. В случае, когда основанием конуса является многоугольник, он превращается в пирамиду.

Рассмотрим некоторые важные понятия.

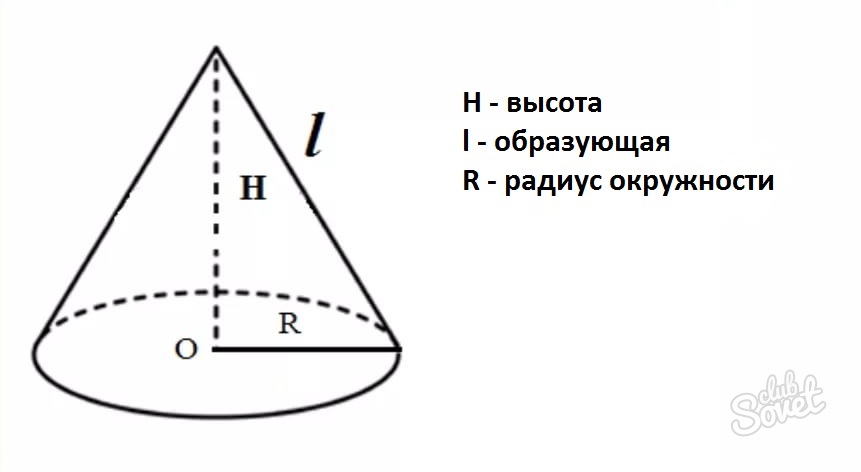
Образующей конуса называется отрезок, который соединяет любую точку границы основания конуса, с его вершиной.
Высотой конуса является перпендикуляр, который опущен из вершины к основанию тела.

Конус бывает нескольких типов:

Прямой, если его основание – одна из таких фигур, как эллипс или круг. Обязательным условием является проецирование вершины конуса в центр основания.

Косой – у него центр фигуры, которая находится в основании, не совпадает с проекцией вершины на это самое основание.

Круговой – отталкиваясь от названия, понятно, что в его основании лежит круг.

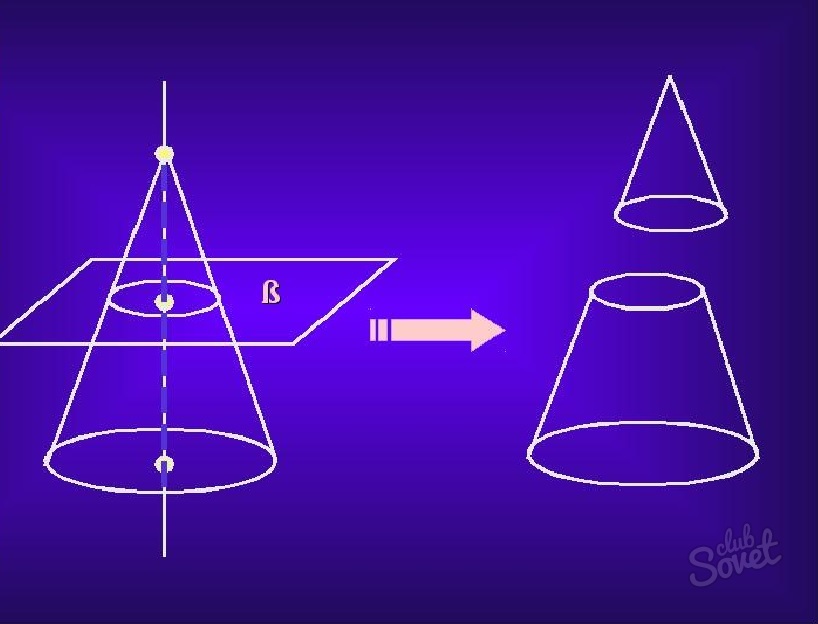
Усеченный – область конуса, лежащая между основанием и сечением плоскости, которая параллельна основанию и пересекает данный конус.

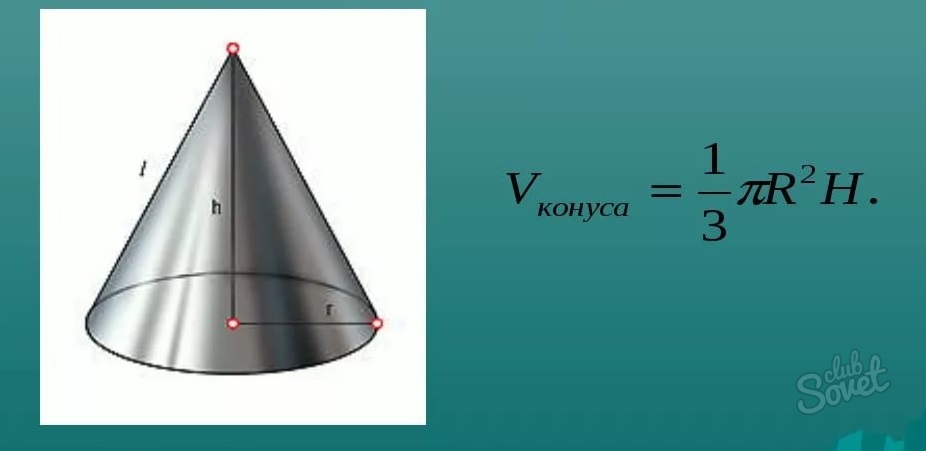
Формула объема прямого конуса

Объем прямого конуса можно рассчитать по следующей формуле:

V=13⋅Sосн⋅hV=frac{1}{3}cdot S_{text{осн}}cdot h

где SоснS_{text{осн}} – площадь основания конуса;
hh – высота конуса.

Рассмотрим несколько примеров.

Задача 1

Найдите объем конуса, если его образующая ll равна 5см5text {см}, а радиус основания RR, которым является круг, равен 3 см3text{ см}.

Решение

l=5l=5
R=3R=3

Сперва найдем высоту конуса hh. Включим его в прямоугольный треугольник, гипотенузой которого является образующая. По теореме Пифагора:

l2=h2+R2l^2=h^2+R^2

Отсюда, hh:

h=l2−R2h=sqrt{l^2-R^2}

h=52−32h=sqrt{5^2-3^2}

h=25−9h=sqrt{25-9}

h=16h=sqrt{16}

h=4h=4

Затем находим площадь основания конуса. Это площадь круга радиуса RR:

Sосн=π⋅R2=π⋅32≈28.26S_{text{осн}}=picdot R^2=picdot3^2approx28.26

Последние вычисления — нахождение объема конуса по формуле:

V=13⋅Sосн⋅h≈13⋅28.26⋅4≈37.68 см3V=frac{1}{3}cdot S_{text{осн}}cdot happroxfrac{1}{3}cdot 28.26cdot 4approx37.68text{ см}^3

Ответ: 37.68 см3.37.68text{ см}^3.

Задача 2

Известен диаметр круга DD лежащего в основании конуса, равен он 8 см8text{ см}. Высота конуса равна 9 см9text{ см}. Найдите его объем.

Решение

D=8D=8
h=9h=9

Найдем радиус RR круга через его диаметр:

R=12⋅D=82=4R=frac{1}{2}cdot D=frac{8}{2}=4

Площадь этого круга и есть основание нашего конуса:

Sосн=π⋅R2=π⋅42≈50.24S_{text{осн}}=picdot R^2=picdot4^2approx50.24

Сам объем равен:

V=13⋅Sосн⋅h≈13⋅50.24⋅9≈150.72 см3V=frac{1}{3}cdot S_{text{осн}}cdot happroxfrac{1}{3}cdot 50.24cdot 9approx150.72text{ см}^3

Ответ: 150.72 см3.150.72text{ см}^3.

Вам нужно решить задачу по алгебре? Наши эксперты помогут вам!

Тест на тему “Объем конуса”

Источник

Объём конуса

Главная
/
Математика
/
Геометрия
/
Объём конуса

Для того чтобы посчитать объём конуса, просто воспользуйтесь нашим удобным онлайн калькулятором:

Онлайн калькулятор

Через площадь основания и высоту

Площадь основания S_осн =
Высота h =

V =

Округление ответа:

Через радиус и другие параметры

=
=

V =

Округление числа π: Округление ответа:

Просто введите данные, и получите ответ.

Теория

Объём конуса через площадь основания и высоту

Чему равен объём конуса V, если площадь его основания S_осн, а высота h:

Формула

V = ⅓ ⋅ S_осн ⋅ h

Пример

Для примера посчитаем, чему равен объём конуса, у которого площадь основания S_осн = 3 см², а высота h = 5 см :

V = ⅓ ⋅ 3 ⋅ 5 = ¹⁵⁄₃ = 5 см³

Объём конуса через образующую и радиус

Чему равен объём конуса V, если его образующая l, радиус основания r?

Формула

V = ⅓ ⋅ π ⋅ r² ⋅ √l² — r²

через диаметр:

V = ⅓ ⋅ π ⋅ (^d/₂)² ⋅ √l² — (d/₂)²

Пример

Для примера посчитаем, чему равен объём конуса, у которого образующая l = 5 см, а радиус основания r = 2 см:

V = ⅓ ⋅ 3.14 ⋅ 2² ⋅ √5² — 2² = ⅓ ⋅ 12.56 ⋅ √21 ≈ 4.19 ⋅ 4.58 ≈ 19.19 см³

Объём конуса через радиус и высоту

Чему равен объём конуса V, если радиус его основания r, а высота h?

Формула

V = ⅓ ⋅ π ⋅ r² ⋅ h

через диаметр:

V = ⅓ ⋅ π ⋅ (^d/₂)² ⋅ h

Пример

Для примера посчитаем объём конуса, у которого высота h = 6 см, а радиус основания r = 3 см:

V = ⅓ ⋅ 3.14 ⋅ 3² ⋅ 6 = ^169.56/₃ = 56.52 см³

Объём конуса через угол раствора (α) и радиус

Чему равен объём конуса V, если угол раствора α, а радиус основания r?

Формула

V = ⅓ ⋅ π ⋅ ^r³/_{tg (^α/₂)}

Пример

Для примера посчитаем объём конуса, имеющего угол раствора α = 30° и радиус основания r = 2 см:

V = ⅓ ⋅ 3.14 ⋅ ^2³/_tg(30/2) ≈ 1,0467 ⋅ 8 / 0.2679 ≈ 31.25 см³

Объём конуса через угол β и радиус

Чему равен объём конуса V, если известны угол β и радиус основания r?

Формула

V = ⅓ ⋅ π ⋅ ^r³/_{tg β}

Пример

Для примера посчитаем объём конуса, имеющего угол β = 20° и радиус основания r = 3 см:

V = ⅓ ⋅ 3.14 ⋅ ^3³/_{tg 20} ≈ 1,0467 ⋅ 27 / 0.36397 ≈ 77.64 см³

Объём конуса через угол γ и радиус

Чему равен объём конуса V, если известны угол γ и радиус основания r?

Формула

V = ⅓ ⋅ π ⋅ r³ ⋅ tg γ

Пример

Для примера посчитаем объём конуса, имеющего угол γ = 45° и радиус основания r = 2 см:

V = ⅓ ⋅ 3.14 ⋅ 2³ ⋅ tg 45 ≈ 1,0467 ⋅ 8 ⋅ 1 ≈ 8.37 см³

См. также

Источник

Чтобы найти объем конуса необходимо произвести дополнительные построения.

Построим вписанную в конус правильную n-угольную пирамиду и опишем вокруг данного конуса правильную n-угольную пирамиду.
Вписанная пирамида содержится в конусе. Из этого следует, что ее объем не больше объема конуса.
Описанная пирамида содержит конус, а это значит, что ее объем не меньше объема конуса.

Впишем в основание вписанной пирамиды окружность.
Если радиус вписанного правильного n-угольника равен R, то радиус вписанной в него окружности будет равен:
$R_vpokr=R*cos{{pi}/n}$

Объем вписанной пирамиды вычисляется по формуле:

где S – основание пирамиды.
Площадь данного круга вычисляется по формуле: $S={pi}*(R{cos{{pi}/n}})^2={pi}R^2{cos^2{{pi}/n}}$
Площадь основания вписанной пирамиды не меньше площади круга, содержащегося в ней
Поэтому утверждение, что объем вписанной в конус пирамиды не меньше ${1/3}{pi}R^2H{cos^2{{pi}/n}}$ верно.
А следовательно, мы может утверждать, что объем конуса, содержащий эту пирамиду будет больше или равен ${1/3}{pi}R^2H{cos^2{{pi}/n}}$
V≥ ${1/3}{pi}R^2Hcos^2{{pi}/n}$

Теперь опишем окружность вокруг основания описанной вокруг конуса пирамиды.
Радиус этой окружности будет равен: $R_{op.okr}= R/ {cos { {pi}/n}}$

Площадь данного круга вычисляется по формуле: $S={pi}(R/{cos{{pi}/n}})^2$
Основание описанной пирамиды содержится в круге описанном вокруг него. Поэтому площадь основания пирамиды не больше ${pi}{{R^2}/{cos^2{{pi}/n}}}$
Поэтому утверждение,что объем описанной пирамиды не больше ${1/3}*{{{pi}HR^2}/{cos^2{{pi}/n}}}$ верно.
А следовательно, мы может утверждать, что объем конуса, содержащий в эту пирамиду будет меньше или равен ${1/3}{{{pi}HR^2}/{cos^2{{pi}/n}}}$
$V<={1/3}{pi}HR^2$
Два полученных неравенства равны при любом n. Если то
Тогда из первого неравенства следует, что V≥ ${1/3}{pi}HR^2$
Из второго неравенства $V<={1/3}{pi}HR^2$

Отсюда следует, что

$V={1/3}{pi}HR^2$

Объем конуса равен одной трети произведения радиуса на высоту.

Пример расчета объема конуса
Найти объем конуса, если его радиус основания равен 3 см, а образующая 5 см.
Объем конуса вычисляется по формуле:
$V={1/3}{pi}HR^2$
Для того, чтобы воспользоваться данной формулой необходимо найти высоту конуса. Образующая конуса, его высота и радиус основания образуют прямоугольный треугольник. Воспользовавшись теоремой Пифагора имеем:

Отсюда:
$H=sqrt{L^2-R^2}=sqrt{5^2-3^2}=sqrt{16}=4$
Подставим значение радиуса и высоты в формулу объема конуса.
Имеем:
$V={1/3}{pi}4*3^2=12{pi}$

Источник

Через образующую и высоту конуса можно найти радиус, построив прямоугольный треугольник, в котором образующая является гипотенузой, а высота и радиус – катетами. Из этого же треугольника становится возможным вычислить угол между образующей и основанием, а для того чтобы найти угол раствора конуса, необходимо вернуться к равнобедренному треугольнику из двух образующих и диаметра, в котором угол раствора будет равен разности двух углов при основании от 180 градусов. (рис.40.1, 40.2)
r=√(l^2-h^2 )
sin⁡β=h/l
α=180°-2β

Теперь, зная радиус конуса, можно найти диаметр, периметр и площадь основания круга, подставив в стандартные формулы квадратный корень, полученный по теореме Пифагора.
d=2r=2√(l^2-h^2 )
P=2πr=2π√(l^2-h^2 )
S_(осн.)=πr^2=π(l^2-h^2)

Площадь боковой поверхности конуса и площадь полной поверхности конуса, выраженные через высоту и образующую, также содержат в формулах вместо радиуса квадратный корень из разности квадратов образующей и высоты.
S_(б.п.)=πrl=πl√(l^2-h^2 )
S_(п.п.)=S_(б.п.)+S_(осн.)=πrl+πr^2=π(lr+r^2 )=π(l√(l^2-h^2 )+l^2-h^2)

Чтобы вычислить объем конуса через высоту и образующую, необходимо умножить треть числа π на высоту и разность квадратов образующей и высоты вместо квадрата радиуса.
V=1/3 S_(осн.) h=(πr^2 h)/3=(πh(l^2-h^2))/3

Радиус сферы, которая может быть вписана в конус, напрямую зависит не только от высоты и образующей, но и от радиуса, поэтому его формула существенно услояжняется наличием радикала, полученного через теорему Пифагора для радиуса конуса. В то же время радиус описанной вокруг конуса сферы зависит только от образующей и высоты, представляя собой отношение квадрата образующей к удвоенной высоте. (рис.40.3, 40.4)
r_1=hr/(l+r)=(h√(l^2-h^2 ))/(l+√(l^2-h^2 ))
R=l^2/2h

Источник

Как найти объем конуса

Среди многообразия геометрических тел одним из самых интересных является конус. Образуется он путем вращения прямоугольного треугольника вокруг одного из своих катетов.

1

Как найти объем конуса – основные понятия

Перед тем, как начать вычисления объема конуса, стоит ознакомиться с основными понятиями.

Круговой конус – основанием такого конуса является круг. Если в основании лежит эллипс, парабола или гипербола, то фигуры называются эллиптическим, параболическим или гиперболическим конусом. Стоит помнить, что два последних вида конуса имеют бесконечный объем.
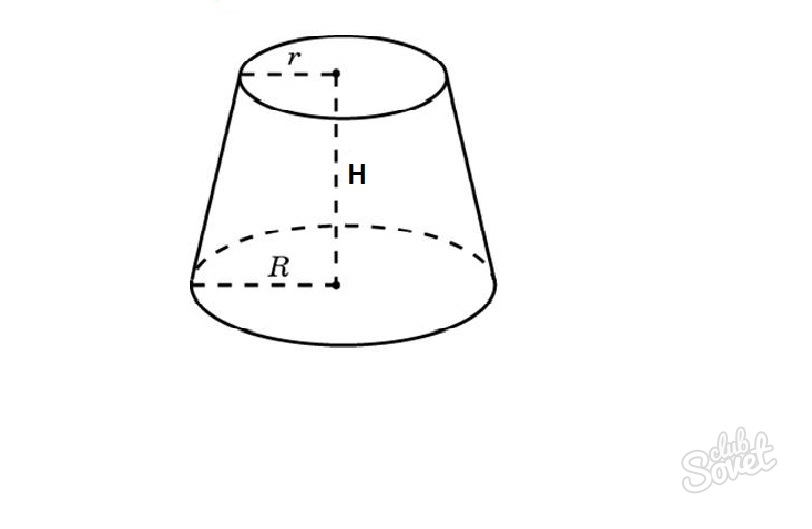
Усеченный конус – часть конуса, расположенная между основанием и плоскостью, параллельной этому основанию, находящейся между вершиной и основанием.
Высота – перпендикулярный основанию отрезок, выпущенный из вершины.
Образующая конуса – отрезок, соединяющий границу основания и вершину.

2

Объем конуса

Для расчета объема конуса применяется формула V=1/3*S*H, где S – площадь основания, H – высота. Так как основание конуса – круг, то его площадь находится по формуле S= nR^2, где n = 3,14, R – радиус окружности.

Бывает ситуация, когда неизвестны какие-то из параметров: высота, радиус или образующая. В таком случае стоит прибегнуть к теореме Пифагора. Осевым сечением конуса является равнобедренный треугольник, состоящий из двух прямоугольных треугольника, где l – гипотенуза, а H и R – катеты. Тогда l=(H^2+R^2)^1/2.

3

Объем усеченного конуса

Усеченный конус представляет собой конус с обрезанной верхушкой.

Чтобы найти объем такого конуса понадобится формула:

V=1/3*n*H*(r^2+rR+R^2),

где n=3.14, r – радиус окружности сечения, R – радиус большого основания, H – высота.

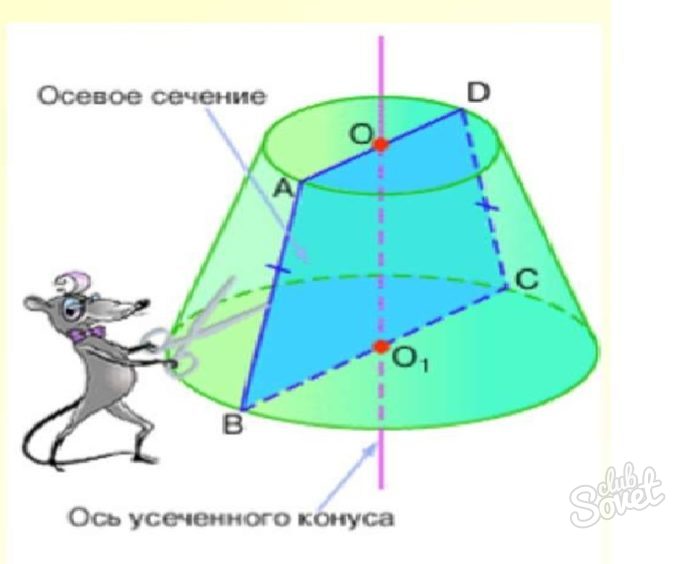
Осевым сечением усеченного конуса будет равнобедренная трапеция. Поэтому, если необходимо найти длину образующей конуса или радиуса одной из окружностей, стоит применять формулы для нахождения боковых сторон и оснований трапеции.

Пример:

Найти объем конуса, если его высота равна 8 см, радиус основания 3 см.

Дано: H=8 см, R=3 см.

Сначала найдем площадь основания, применив формулу S=nR^2.

S=3.14*3^2=28.26 см^2

Теперь по формуле V=1/3*S*H находим объем конуса.

V=1/3*28.26*8=75.36 см^3

Фигуры в форме конуса встречаются повсюду: парковочные конусы, башни строений, абажур светильника. Поэтому знание, как найти объем конуса, порой может пригодиться как в профессиональной, так и в повседневной жизни.

Источник

Онлайн-калькулятор объема конуса

Формула объема прямого конуса

Тест на тему “Объем конуса”

Объём конуса

Онлайн калькулятор

Через площадь основания и высоту

Через радиус и другие параметры

Теория

Объём конуса через площадь основания и высоту

Формула

Пример

Объём конуса через образующую и радиус

Формула

Пример

Объём конуса через радиус и высоту

Формула

Пример

Объём конуса через угол раствора (α) и радиус

Формула

Пример

Объём конуса через угол β и радиус

Формула

Пример

Объём конуса через угол γ и радиус

Формула

Пример

См. также

Как найти объем конуса

1 Как найти объем конуса – основные понятия

2 Объем конуса

3 Объем усеченного конуса

Не пропустите также:

1

Как найти объем конуса – основные понятия

2

Объем конуса

3

Объем усеченного конуса