Объём конуса
- Главная
- /
- Математика
- /
- Геометрия
- /
- Объём конуса
Для того чтобы посчитать объём конуса, просто воспользуйтесь нашим удобным онлайн калькулятором:
Онлайн калькулятор
Через площадь основания и высоту
Площадь основания Sосн =
Высота h =
V =
0
Округление ответа:
Через радиус и другие параметры
=
=
V =
0
Округление числа π: Округление ответа:
Просто введите данные, и получите ответ.
Теория
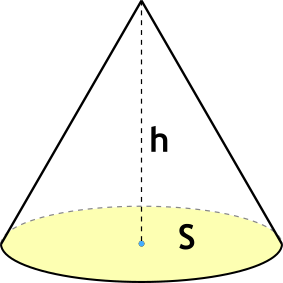
Объём конуса через площадь основания и высоту
Чему равен объём конуса V, если площадь его основания Sосн, а высота h:
Формула
V = ⅓ ⋅ Sосн ⋅ h
Пример
Для примера посчитаем, чему равен объём конуса, у которого площадь основания Sосн = 3 см², а высота h = 5 см :
V = ⅓ ⋅ 3 ⋅ 5 = 15⁄3 = 5 см³
Объём конуса через образующую и радиус
Чему равен объём конуса V, если его образующая l, радиус основания r?
Формула
V = ⅓ ⋅ π ⋅ r² ⋅ √l² — r²
через диаметр:
V = ⅓ ⋅ π ⋅ (d/2)² ⋅ √l² — (d/2)²
Пример
Для примера посчитаем, чему равен объём конуса, у которого образующая l = 5 см, а радиус основания r = 2 см:
V = ⅓ ⋅ 3.14 ⋅ 2² ⋅ √5² — 2² = ⅓ ⋅ 12.56 ⋅ √21 ≈ 4.19 ⋅ 4.58 ≈ 19.19 см³
Объём конуса через радиус и высоту
Чему равен объём конуса V, если радиус его основания r, а высота h?
Формула
V = ⅓ ⋅ π ⋅ r² ⋅ h
через диаметр:
V = ⅓ ⋅ π ⋅ (d/2)² ⋅ h
Пример
Для примера посчитаем объём конуса, у которого высота h = 6 см, а радиус основания r = 3 см:
V = ⅓ ⋅ 3.14 ⋅ 3² ⋅ 6 = 169.56/3 = 56.52 см³
Объём конуса через угол раствора (α) и радиус
Чему равен объём конуса V, если угол раствора α, а радиус основания r?
Формула
V = ⅓ ⋅ π ⋅ r³/tg (α/2)
Пример
Для примера посчитаем объём конуса, имеющего угол раствора α = 30° и радиус основания r = 2 см:
V = ⅓ ⋅ 3.14 ⋅ 2³/tg(30/2) ≈ 1,0467 ⋅ 8 / 0.2679 ≈ 31.25 см³
Объём конуса через угол β и радиус
Чему равен объём конуса V, если известны угол β и радиус основания r?
Формула
V = ⅓ ⋅ π ⋅ r³/tg β
Пример
Для примера посчитаем объём конуса, имеющего угол β = 20° и радиус основания r = 3 см:
V = ⅓ ⋅ 3.14 ⋅ 3³/tg 20 ≈ 1,0467 ⋅ 27 / 0.36397 ≈ 77.64 см³
Объём конуса через угол γ и радиус
Чему равен объём конуса V, если известны угол γ и радиус основания r?
Формула
V = ⅓ ⋅ π ⋅ r³ ⋅ tg γ
Пример
Для примера посчитаем объём конуса, имеющего угол γ = 45° и радиус основания r = 2 см:
V = ⅓ ⋅ 3.14 ⋅ 2³ ⋅ tg 45 ≈ 1,0467 ⋅ 8 ⋅ 1 ≈ 8.37 см³
См. также
Конус – это тело в пространстве, образованное путем вращения прямоугольного треугольника вокруг одного из его катетов.
Онлайн-калькулятор объема конуса
Конус – это тело, образованное совокупностью всех лучей, исходящих из точки пространства и пересекающих плоскость.
Точка, из которой лучи исходят, получила название вершины конуса. В случае, когда основанием конуса является многоугольник, он превращается в пирамиду.
Рассмотрим некоторые важные понятия.
Образующей конуса называется отрезок, который соединяет любую точку границы основания конуса, с его вершиной.
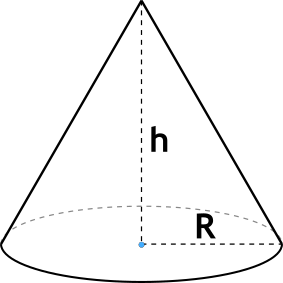
Высотой конуса является перпендикуляр, который опущен из вершины к основанию тела.
Конус бывает нескольких типов:
Прямой, если его основание – одна из таких фигур, как эллипс или круг. Обязательным условием является проецирование вершины конуса в центр основания.
Косой – у него центр фигуры, которая находится в основании, не совпадает с проекцией вершины на это самое основание.
Круговой – отталкиваясь от названия, понятно, что в его основании лежит круг.
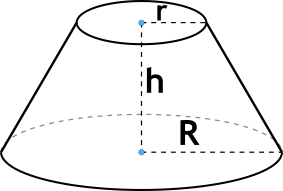
Усеченный – область конуса, лежащая между основанием и сечением плоскости, которая параллельна основанию и пересекает данный конус.
Формула объема прямого конуса
Объем прямого конуса можно рассчитать по следующей формуле:
V=13⋅Sосн⋅hV=frac{1}{3}cdot S_{text{осн}}cdot h
где SоснS_{text{осн}} – площадь основания конуса;
hh – высота конуса.
Рассмотрим несколько примеров.
Найдите объем конуса, если его образующая ll равна 5см5text {см}, а радиус основания RR, которым является круг, равен 3 см3text{ см}.
Решение
l=5l=5
R=3R=3
Сперва найдем высоту конуса hh. Включим его в прямоугольный треугольник, гипотенузой которого является образующая. По теореме Пифагора:
l2=h2+R2l^2=h^2+R^2
Отсюда, hh:
h=l2−R2h=sqrt{l^2-R^2}
h=52−32h=sqrt{5^2-3^2}
h=25−9h=sqrt{25-9}
h=16h=sqrt{16}
h=4h=4
Затем находим площадь основания конуса. Это площадь круга радиуса RR:
Sосн=π⋅R2=π⋅32≈28.26S_{text{осн}}=picdot R^2=picdot3^2approx28.26
Последние вычисления — нахождение объема конуса по формуле:
V=13⋅Sосн⋅h≈13⋅28.26⋅4≈37.68 см3V=frac{1}{3}cdot S_{text{осн}}cdot happroxfrac{1}{3}cdot 28.26cdot 4approx37.68text{ см}^3
Ответ: 37.68 см3.37.68text{ см}^3.
Известен диаметр круга DD лежащего в основании конуса, равен он 8 см8text{ см}. Высота конуса равна 9 см9text{ см}. Найдите его объем.
Решение
D=8D=8
h=9h=9
Найдем радиус RR круга через его диаметр:
R=12⋅D=82=4R=frac{1}{2}cdot D=frac{8}{2}=4
Площадь этого круга и есть основание нашего конуса:
Sосн=π⋅R2=π⋅42≈50.24S_{text{осн}}=picdot R^2=picdot4^2approx50.24
Сам объем равен:
V=13⋅Sосн⋅h≈13⋅50.24⋅9≈150.72 см3V=frac{1}{3}cdot S_{text{осн}}cdot happroxfrac{1}{3}cdot 50.24cdot 9approx150.72text{ см}^3
Ответ: 150.72 см3.150.72text{ см}^3.
Вам нужно решить задачу по алгебре? Наши эксперты помогут вам!
Тест на тему “Объем конуса”
Данный калькулятор предназначен для расчёта объёма прямого кругового конуса. Он умеет делать расчёт двумя способами: через площадь основания и через радиус основания конуса.
Каким способом считать:
Через радиус основания
Через площадь основания
Укажите размеры:
Радиус основания
Высота
Округлить число Пи до 3,14
Объём:
Решение:
Ссылка на страницу с результатом:
# Теория
Конус — это геометрическое тело, образуемое вращением прямоугольного треугольника вокруг катета.
Круглый конус может быть получен вращением прямоугольного треугольника вокруг одного из его катетов, поэтому круглый конус называт также конусом вращения.
Образующая конуса — отрезок, соединяющий вершину и границу основания.
Образующая (или боковая) поверхность конуса — объединение образующих конуса; образующая поверхность конуса является конической поверхностью.
Высота конуса — отрезок, опущенный перпендикулярно из вершины на плоскость основания (а также длина такого отрезка).
Угол раствора конуса — угол между двумя противоположными образующими (угол при вершине конуса, внутри конуса).
Конусность — соотношение высоты и диаметра основания конуса.
Прямой конус — конус, основание которого имеет центр симметрии (например, является кругом или эллипсом) и ортогональная проекция вершины конуса на плоскость основания совпадает с этим центром; при этом прямая, соединяющая вершину и центр основания, называется осью конуса.
Косой (или наклонный) конус — конус, у которого ортогональная проекция вершины на основание не совпадает с его центром симметрии.
Круговой конус — конус, основание которого является кругом.
Конус, опирающийся на эллипс, параболу или гиперболу, называют соответственно эллиптическим, параболическим и гиперболическим конусом: последние два имеют бесконечный объём.
Усечённый конус или конический слой — часть конуса, лежащая между основанием и плоскостью, параллельной основанию и находящейся между вершиной и основанием.
Формула объёма конуса
h
r
V = dfrac{1}{3} cdot pi cdot r^2 cdot h
- V — объём конуса
- π — число Пи (≈ 3,14)
- r — радиус основания конуса
- h — высота конуса
V = dfrac{1}{3} cdot S cdot h
- V — объём конуса
- h — высота конуса
- S — площадь основания конуса
Похожие калькуляторы:
Войдите чтобы писать комментарии

{V=dfrac {1}{3} pi r^2 h}
Конус — это трехмерная фигура, в основании которой лежит круг. Чтобы найти объем конуса достаточно знать два параметра — высоту (h) и радиус основания (r).
Содержание:
- калькулятор объема конуса
- формула объема конуса через высоту и радиус
- формула объема конуса через площадь основания и высоту
- формула объёма усеченного конуса
- примеры задач
Если мы сравним формулу объема конуса с формулой объема цилиндра, то мы увидим, что объем конуса в 3 раза меньше объема цилиндра с той же высотой и радиусом основания.
Наш калькулятор может рассчитать объем конуса через радиус основания и высоту, площадь основания и высоту, а также объем усеченного конуса через его высоту и радиусы нижнего и верхнего оснований.
Кроме того объем конуса можено найти, подставив значения в формулы, приведенные ниже.
Формула объёма конуса через радиус и высоту
{V=frac {1}{3} pi r^2 h}
r — радиус основания конуса,
h — высота конуса
Формула объёма конуса через площадь основания и высоту
{V=frac {1}{3} S h}
S — площадь основания конуса,
h — высота конуса
Формула объёма усеченного конуса
{V=frac {1}{3} pi h(r^2 + r R + R^2)}
h — высота усеченного конуса,
r — радиус меньшего основания усеченного конуса,
R — радиус большего основания усеченного конуса.
Примеры задач на нахождение объема конуса
Задача 1
Найдем объем конуса, высота которого 30см, а радиус основания 20см.
Решение
Подставим эти значения в формулу и произведем расчет:
V=dfrac {1}{3} pi r^2 h = dfrac {1}{3} cdot pi cdot 20^2 cdot 30 = dfrac {1}{3} cdot pi cdot 12000 = 400 pi : см^3 approx 12 566,37 : см^3
Ответ: {400 pi : см^3 approx 12 566,37 : см^3}
Проверить результат можно с помощью калькулятора .
Задача 2
Найдем объем конуса с высотой 3 см и диаметром основания 8 см².
Решение
Подставим эти значения в формулу и произведем расчет:
V=dfrac {1}{3} S h = dfrac {1}{3} cdot 8 cdot 3 = dfrac {1}{3} cdot 24 = 8 : см^3
Ответ: 8 см³
Воспользуемся калькулятором для проверки результата.
Задача 3
Найдите объем усеченного конуса радиусы оснований которого равны 1 см и 2 см, а высота равна 3 см.
Решение
Подставим высоту и радиусы оснований в формулу и произведем расчет:
V=dfrac {1}{3} pi h(r^2 + r R + R^2) = dfrac {1}{3} pi cdot 3 cdot (1^2 + 1 cdot 2 + 2^2) = dfrac {1}{3} pi cdot 3 cdot (1 + 2 + 4) = dfrac {1}{3} pi cdot 3 cdot 7 = dfrac {1}{3} pi cdot 21 = 7 pi : см^3 approx 21,99115 : см^3
Ответ: {7 pi : см^3 approx 21,99115 : см^3}
Проверим полученный ответ.
Поскольку объем конуса равен произведению высоты на треть площади основания конуса, то, зная объем и высоту, легко найти площадь круга в основании, а затем радиус и диаметр конуса.
S_(осн.)=3V/h
r=√(S_(осн.)/π)=√(3V/πh)
d=2r=2√(3V/πh)
Чтобы найти образующую конуса через объем и высоту, необходимо построить прямоугольный треугольник с образующей в виде гипотенузы и радиусом и высотой как катетами треугольника. Тогда образующая будет равна квадратному корню из суммы квадратов высоты и радиуса по теореме Пифагора, а угол между основанием и образующей можно будет найти через тангенс отношения высоты к радиусу. (рис.40.1)
l=√(h^2+r^2 )=√(h^2+3V/πh)
tanβ=h/r=h/√(3V/πh)=h√(πh/3V)
Угол раствора конуса можно найти, зная угол между образующей и основанием, и соединив их в равнобедренном треугольнике, где боковой стороной будет образующая, а основанием треугольника – диаметр конуса. (рис.40.2)
α=180°-2β
Площадь боковой поверхности конуса равна произведению радиуса на образующую и число π, а площадь полной поверхности представляет собой сумму площади боковой поверхности и площади основания, которую можно найти через объем.
S_(б.п.)=πrl=π√(3V/πh (h^2+3V/πh) )
S_(п.п.)=S_(б.п.)+S_(осн.)=π√(3V/πh (h^2+3V/πh) )+3V/h
Радиусы вписанной и описанной около конуса сфер можно найти из отношений, связывающих не только высоту конуса, которая известна, но и образующую, а также радиус основания конуса. (рис.40.3,40.4)
r_1=hr/(l+r)=(h√(3V/πh))/(√(h^2+3V/πh)+√(3V/πh))=(h√3V)/(√(πh^3+3V)+√3V)
R=(h^2+3V/πh)/2h