Долго жмите на любое свободное место на рабочем столе. Внизу экрана появится несколько иконок, среди которых будут «Виджеты». Нажмите туда, пролистайте варианты снизу, найдите виджеты «Google», ещё раз нажмите на них и выберите поисковую строку.
Как найти объем через массу и толщину?
Смотря что известно о теле, объем которого вы хотите вычислить.
- Зная массу и плотность V = m/ρ, где m — масса, а ρ — плотность
- Для геометрических фигур, например куб V = a^3 перемножить три стороны, а для цилиндра V = S*H площадь основания помножить на высоту
Как найти объем с помощью толщины?
Объем = Площадь х Толщина.
Как найти объем по площади и высоте?
Математически корректный ответ — взять интеграл по площади комнаты (от 0 до 2,5 метров) , наиболее популярный — умножить площадь комнаты на её высоту. Площадь умножить на высоту. 2,5 х 20 =50 куб. м.
Как найти массу зная плотность и толщину?
То есть воспользуйтесь формулой: m = V / ρ, где:V – объем, ρ – плотность, V – объем. Перед расчетом массы приведите все единицы измерения в одну систему, например, в интернациональную систему измерения (СИ).
Как выразить массу через площадь?
Массу ( m ) делим на ( p ) плотность. Получаем ( v )объём, ( v ) объем делим на ( h ) высоту , получаем ( S ) площадь.
Как найти объем по длине ширине и высоте?
Как уже упоминалось, формула расчета объема выглядит следующим образом: V = Длина x Ширина x Высота; поэтому для получения объема необходимо просто перемножить все три стороны.
Как найти объем в физике Зная длину ширину и высоту?
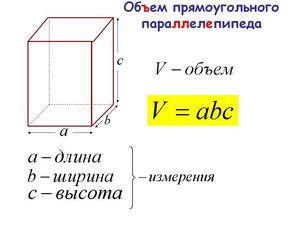
Формулой это можно выразить так: V = a*b*c, где a, b и с — это параметры. Для большей наглядности можно рассмотреть пример: Имеется прямоугольный параллелепипед, площадь основания которого равна 42 см², а его высота составляет 15 см, требуется найти объем исходной фигуры.
Какая формула объема куба?
Куб – это геометрическая фигура, которая представляет собой правильный многогранник, где каждая его грань является квадратом. Объем куба можно вычислить, зная только значение длины его ребра. Так как все его ребра между собой равны. Говоря проще объем куба приравнивается кубу длины его ребра.
Как вычислить массу зная площадь и плотность?
Нужна плотность вещества. Плотность умноженная на объем (площадь умноженная на высоту) и даст массу.
Как найти массу тела в физике?
Чтобы найти массу тела нежно его плотность умножить на объем. Чтобы найти объем тела, нужно его массу разделить на плотность.
Введите а — длину прямоугольника в мм (миллиметрах):
Введите b — ширину прямоугольника в мм (миллиметрах):
Введите h — толщину прямоугольника в мм (миллиметрах):
Как рассчитать объем прямоугольника?
Если прямоугольник имеет толщину, то фактически это параллелепипед. Объем параллелепипед в общем случае рассчитывается по формуле:
V = a x b х h
V — объем параллелепипеда . Объем прямоугольника имеющего толщину (высоту).
a — длина прямоугольника основания параллелепипеда
b — ширина прямоугольника основания параллелепипеда
h — высота параллелепипеда. Толщина прямоугольника.
Объем в миллиметрах кубических прямоугольника имеющего толщину (параллелепипед):
Vмм3 = aмм х bмм х hмм
Vмм3 — объем в миллиметрах кубических (мм3).
aмм — длина прямоугольника в миллиметрах (мм).
bмм — ширина прямоугольника в миллиметрах (мм).
hмм — толщина прямоугольника в миллиметрах (мм).
Объем в сантиметрах кубических прямоугольника имеющего толщину (параллелепипед):
Vсм3 = aмм х bмм х hмм / 1 000
Vсм3 — объем в сантиметрах кубических (см3).
aмм — длина прямоугольника в миллиметрах (мм).
bмм — ширина прямоугольника в миллиметрах (мм).
hмм — толщина прямоугольника в миллиметрах (мм).
Объем в метрах кубических прямоугольника имеющего толщину (параллелепипед):
Vм3 = aмм х bмм х hмм / 1 000 000 000
Vм3 — объем в метрах кубических (м3).
aмм — длина прямоугольника в миллиметрах (мм).
bмм — ширина прямоугольника в миллиметрах (мм).
hмм — толщина прямоугольника в миллиметрах (мм).
Объем в литрах прямоугольника имеющего толщину (параллелепипед):
Vл = aмм х bмм х hмм / 1 000 000
Vл — объем в литрах (л).
aмм — длина прямоугольника в миллиметрах (мм).
bмм — ширина прямоугольника в миллиметрах (мм).
hмм — толщина прямоугольника в миллиметрах (мм).
|
Один метр кубический является единицей объема. Чтобы найти объем какого-то предмета, имеющего КУБИЧЕСКУЮ форму (например, параллелепипед), нужно его длину (в метрах) умножить на ширину (тоже в метрах) и умножить на высоту (опять в метрах). Логично, не правда ли, что метр, умноженный сам на себя три раза превращается в метр кубический! Если требуется посчитать объем предмета НЕ КУБИЧЕСКОЙ формы (например, шар, призма, конус), то для вычисления их объема есть специальные формулы. Если они вам нужны, то советую посмотреть учебник по геометрии. автор вопроса выбрал этот ответ лучшим Ксарфакс 5 лет назад Думаю, всем понятно, что формула расчёта объёма в кубических метрах для каждой геометрической фигуры будет разной. Поэтому нужно произвести все необходимые измерения, а затем воспользоваться соответствующей формулой. Если фигура имеет неправильную формулу, то разбиваем её на несколько стандартных фигур, а затем складываем их объёмы между собой. Нужно помнить, что все измерения проводятся именно в метрах. Например, если высота объекта 70 см, то её нужно перевести в метры: 70 см = 0,7 м. Самый простейший пример — объём помещения Для того, чтобы посчитать объём, нужно воспользоваться формулой нахождения объёма прямоугольного параллелепипеда. V = abc. a — длина, b — ширина, c — высота. Таким образом, измеряем длину / ширину / высоту комнаты, а затем перемножаем эти значения между собой. Если вы знаете площадь, то посчитать объём ещё проще — достаточно измерить высоту и умножить это значение на данное значение. Например, длина комнаты = 6 м, ширина = 5 м, высота = 2,5 м. V = 6 * 5 * 2,5 = 75 м³. Nelli4ka 5 лет назад Для примера возьмем прямоугольник и параллелепипед. Прямоугольник лежит на плоскости, и мы можем найти либо его периметр (т.е. длину всех сторон данной фигуры), либо его площадь, которая будет выражаться, скажем, в сантиметрах или метрах квадратных. Параллелепипед — фигура трехмерного пространства, у нее есть помимо ширины и длины еще и высота. Когда значения высоты, длины и ширины умножаются друг на друга, находится объем трехмерной фигуры, которая уже будет выражаться не в квадратных, а в кубических сантиметрах, метрах и т.д., но для каждого некубического случая существует своя индивидуальная формула. Galina7v7 7 лет назад Если ваш вопрос трактовать так: «как посчитать объём 1 метра кубического , то V = 1м * 1 м = 1м = 1 м ^3 (1 метр кубический ) , и это единица измерения объёма в системе СИ. Если вас интересует тело в форме параллелепипеда ,где все соседние ребра перпендикулярны друг другу , то объём такого тела определяется путём произведения : длина *ширина * высота. ОБЪЁМ ТЕЛА = ДЛИНА (м) х ШИРИНА (м) х ВЫСОТА (м)Для того,чтобы получить объём в м^3 нужно все 3 параметра тоже выразить в метрах. Zolotynka 5 лет назад В метрах кубических можно высчитать объем предмета, который представляет собой форму куба. Для этого следует воспользоваться формулой: длина*ширина*высота. ** Данная формула имеет важное практическое значение. Рассмотрим на примере: Предположим, нам нужно рассчитать, расход бетона для того, чтобы сделать пол в сарае, размер которого: ширина 2.0 м, длина 2.0 м, а желаемая толщина бетона — 100 мм. Формула для расчета объема бетона в м3 будет выглядеть следующими образом: 2,0 × 2,0 × 0,1 = 0.4m3 Математика обязательный предмет в школьной программе, но знания уходят, забываются формулы, как проводить вычисления уже не каждый вспомнит, остается в голове то, что используется нами ежедневно, и на работе требуется все время, поэтому формула расчета кубического метра может придти в голову не сразу, и придется искать эту информацию, для тех, кому нужно — длину умножить на ширину и умножить на высоту. Kerbal Space Program 6 лет назад Крайне просто. Для этого достаточно брать длины и расстояния в метрах: будь то длина, высота и ширина или же радиус, при вычислении объема круга или цилиндра. Например, имеем: Параллелепипед длиной 1245 см, шириной 3 см и высотой 25 см. Эти длины переведем в метры и получим:
Считаем теперь объем: V=1,245*0,03*0,25=0,00933 метра кубических. moreljuba 5 лет назад Посчитать объём в метрах кубических вы вполне спокойно можете. Для это вам необходимо иметь представление о значениях для таких величин как высота, ширина (толщина) и длина. Переводите в метры и перемножаете эти три составляющие и получаете в результате объём в метрах кубических. FantomeRU 5 лет назад Чтобы вычислить объем необходимо умножить длину на ширину и на высоту. При этом, чтобы искомый результат был в кубических метрах, сначала нужно все стороны данного предмета выразить в метрах и только потом перемножать. vksvovko 6 лет назад Один из распространенных способов найти объем предмета неправильной формы — это налить воду в измерительный сосут и опустить туда предмет. далее смотрим сколько он вытеснил воды и легко подсчитываем объем в м3. EvgeniyAlekseevich 7 лет назад Высоту, выраженную в м3, умножить на длину и умножить на ширину. Знаете ответ? |
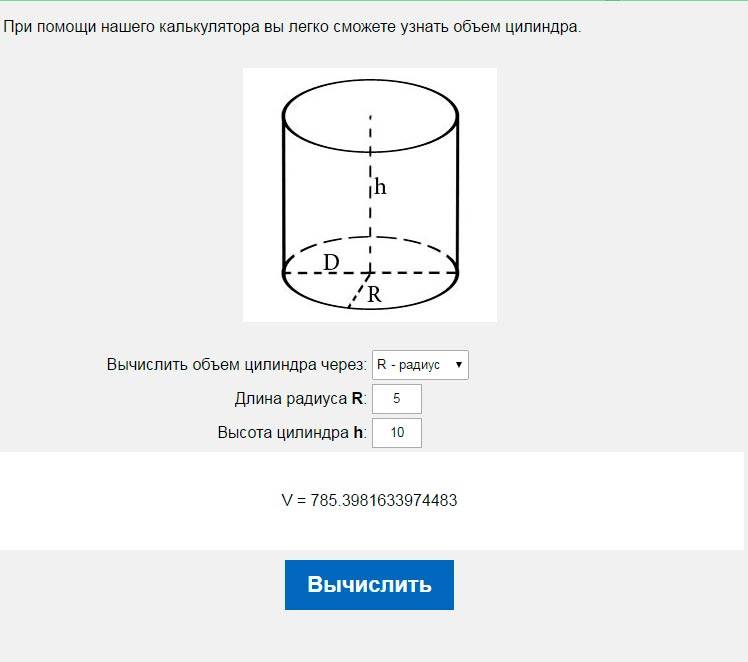
При помощи нашего калькулятора вы легко сможете узнать объем цилиндра. Так же если вам необходимо узнать объем бочки, круглой цистерны, круглого бака и т.д., то это калькулятор то, что Вам нужно.
|
|
|
| Вычислить объем цилиндра через: | |
| Длина радиуса R: | |
| Высота цилиндра h: |
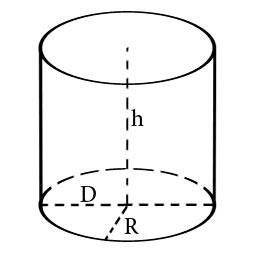
Для того что бы вычислить объем цилиндра необходимо знать его высоту и радиус или диаметр. Если нам известны указанные величины, для нас не составит труда вычислить объем.
Объем цилиндра рассчитывается по следующим формулам:
- Если нам известен радиус:
V=πR2h
- Если нам известен диаметр:
V=πD2/4h
Где V – объем, R – радиус, D – диаметр, h — высота, π – число Пи которое всегда примерно равно 3,14.
Расчет объема цилиндра |
 |
Школа — это необъятная чаша знаний, которая включает в себя множество дисциплин, которые могут заинтересовать любого ребенка. Математика — царица точных наук. Строгая и дисциплинированная, она не терпит неточностей. Даже повзрослев, в обычной жизни мы можем столкнуться с разными математическими проблемами: вычисление квадратных метров для укладки плитки в ванной, кубических метров для определения объема бака и т. д., чего уж говорить о школьниках, которые только-только начинают свой математический путь.
Очень часто, начав изучать математику, точнее, геометрию, ученики путают плоские фигуры с объемными. Куб называют квадратом, шар — кругом, параллелепипед обычным прямоугольником. И здесь есть свои тонкости.
Сложно помочь ребенку в выполнении домашнего задания, не зная точно, объем или площадь какой фигуры — плоской или же объемной, нужно найти. Невозможно найти объем плоских фигур, таких как квадрат, круг, прямоугольник. В их случае можно найти лишь площадь. Прежде чем переходить к выполнению задачи, следует подготовить нужные атрибуты:
- Линейка, для того чтобы измерить необходимые нам данные.
- Калькулятор, для того чтобы в дальнейшем подсчитать расчеты.
Содержание:
- Вычисление объема прямоугольного параллелепипеда
- Пример первый
- Пример второй
- Пример третий
Вычисление объема прямоугольного параллелепипеда
Итак, вы знаете, что нужно рассчитать объем, но не забывайте, что обязательно нужно уточнить о какой именно фигуре идет речь: объем куба, или же объемного прямоугольника. Ведь расчет этих, казалось бы, одинаковых фигур, абсолютно разный.
Для начала рассмотрим само понятие объемного прямоугольника. Это параллелепипед. В его основании находится параллелограмм. Так как таковых у него шесть, следовательно все параллелограммы являются гранями параллелепипеда.
Что касается его граней, они могут отличаться, то есть, если прямые боковые грани представляют собой прямоугольники, тогда это прямой параллелепипед, ну, а если все шесть граней являются прямоугольниками, то перед нами прямоугольный параллелепипед.
- После прочтения задачи, нужно определить что именно следует найти; длину фигуры, объем или же площадь.
- Какая именно часть фигуры рассматривается в задаче — ребро, вершина, грань, сторона, а может быть, вся фигура целиком?
Определив все поставленные задачи, можно переходить непосредственно к вычислениям. Для этого нам понадобятся специальные формулы. Итак, для того чтобы найти объем прямоугольного параллелепипеда перемножается между собой длина, ширина и высота (то есть толщина фигуры). Формула вычисления объема прямоугольного параллелепипеда следующая:
V=a*b*h,
V является объемом параллелепипеда, где a — его длина b — ширина и h — высота соответственно.
Важно! Перед началом перевести все измерения в одну единицу исчисления. Ответ должен получится непременно в кубических единицах.
Пример первый
Определим объем бака для спирта, при следующих размерах:
- длина три метра;
- ширина два метра пятьдесят сантиметров;
- высота триста сантиметров.
Для начала обязательно согласовываем единицы измерения и перемножаем их:
3*2.5*3.
Перемножив данные, мы получим ответ в кубических метрах, то есть 3*2.5*3= 22.5 метра в кубе.
Пример второй
Шкаф имеет высоту четыре метра, ширину семьдесят сантиметров и глубину 80 сантиметров.
Зная формулу вычисления можно произвести умножение. Но не стоит торопиться, как и было сказано вначале, следует согласовать между собой единицы, то есть при желании вычислять в сантиметрах перевести все исчисления в сантиметры, ежели в метрах, то в метры. Сделаем оба варианта.
Итак, начнем с сантиметров. Переводим метры в сантиметры:
V = 400 * 70 * 80;
V = 2240000 сантиметров в кубе.
Теперь метры:
V = 4* 0.7 * 0.8;
V = 2.24 метра в кубе.
Исходя из вышеперечисленных манипуляции, очевидно, что работа с кубическими метрами более легка и понятна.
Пример третий
Дана комната, объем которой должен быть вычислен. Длина этой комнаты равна пяти метрам, ширина — трем, а высота потолка 2,5. Опять используем известную нам формулу:
V = a * b * h;
где, а длина комната и равна 5, b- ширина и равна 3 и h высота, которая равна 2.5
Так как все единицы даны в метрах, можно сразу приступать к вычислениям. Перемножая между собой a, b и h:
V = 5 * 3 * 2.5;
V = 37.5 метра в кубе.
Итак, в качестве заключения, можно сказать, что зная основные математические правила для вычисления объема или же площади фигур, а также правильно определив фигуры (плоские или же объемные), умея переводить сантиметры в метры и наоборот — можно облегчить изучение геометрии вашему ребенку, что не может не сделать этот процесс более интересным и привлекательным, ведь все накопленные знания в школе, могут быть успешно использованы в самой обычной бытовой жизни в будущем.