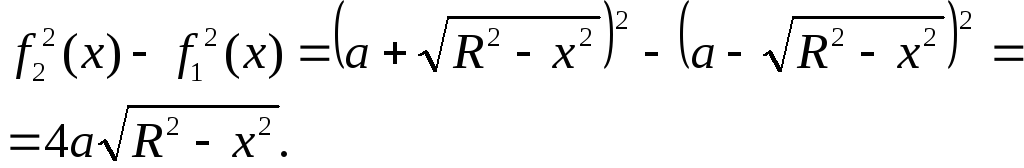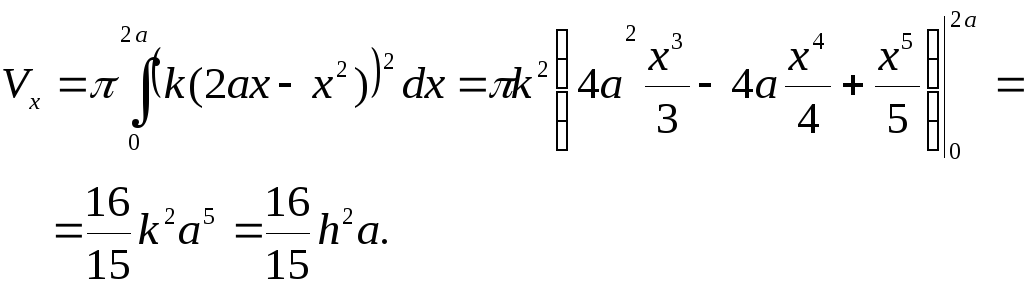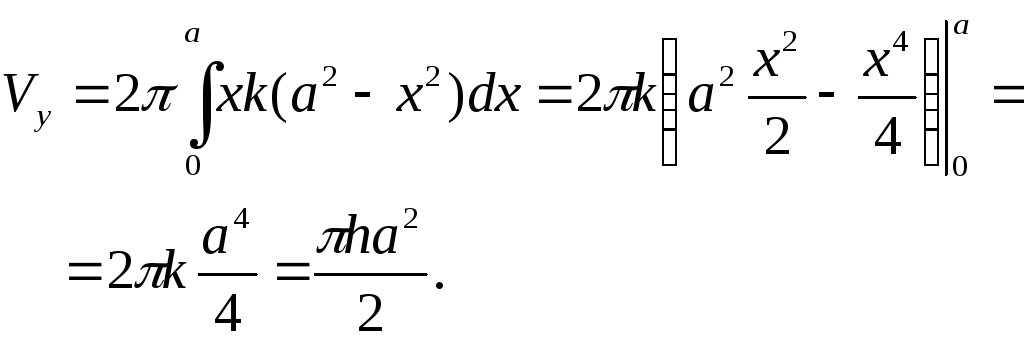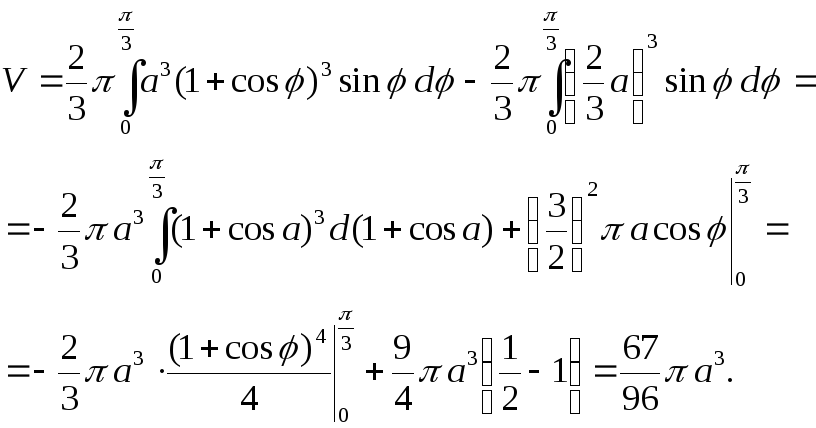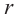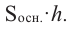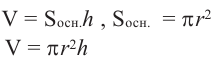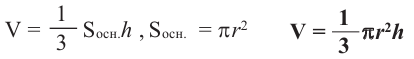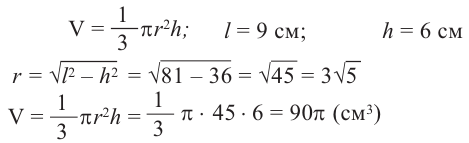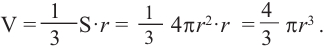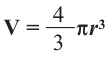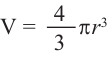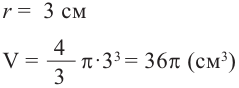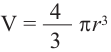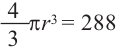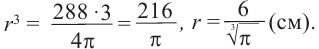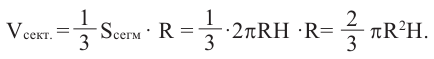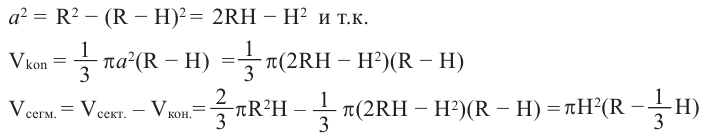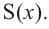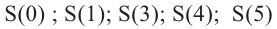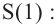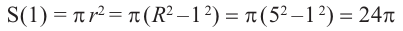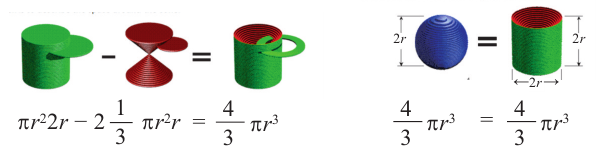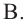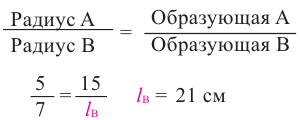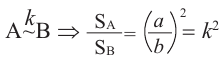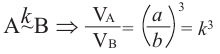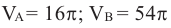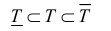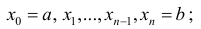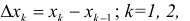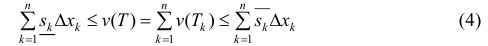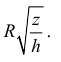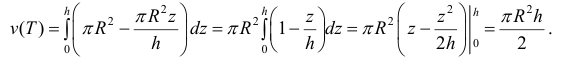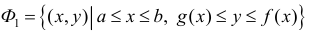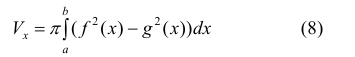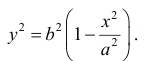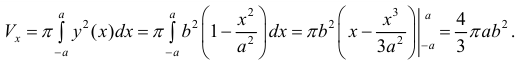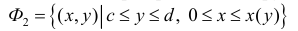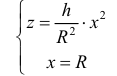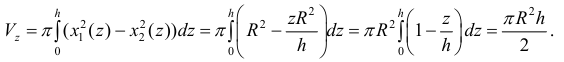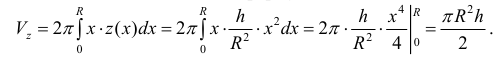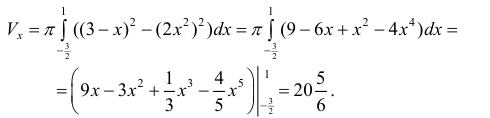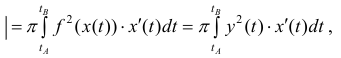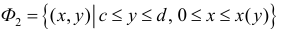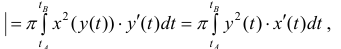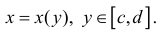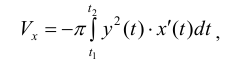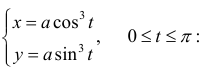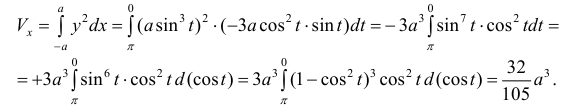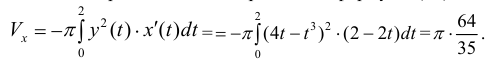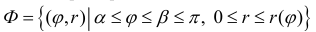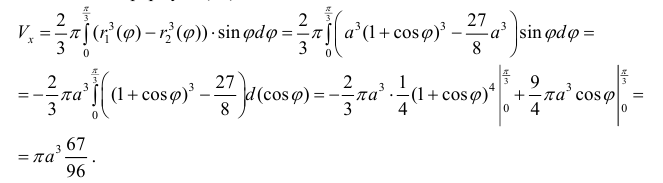Дополнения
1.О применении определённого интеграла для нахождения объёмов тел вращения
1.1.Формула объёма тела вращения
В п.16.2 дано определение тела вращения.
Получим формулу для вычисления объёма тела вращения, применяя интеграл, о котором вам рассказали в курсе «Алгебры и начал математического анализа».
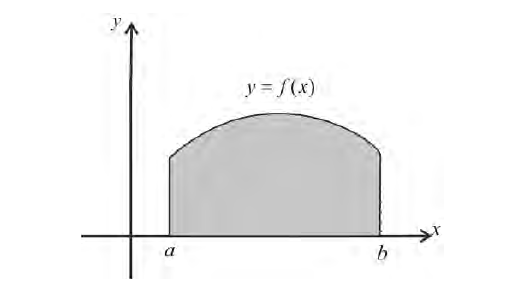
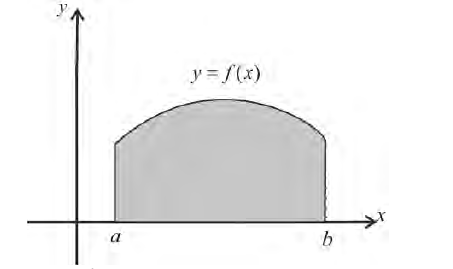
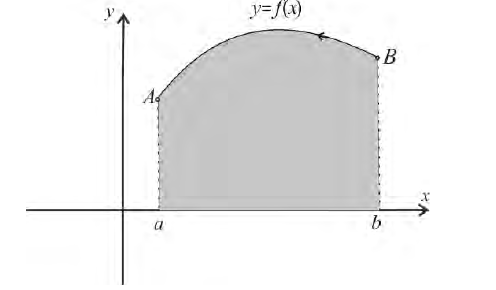
Пусть f(x) — непрерывная на отрезке [a; b] функция, не принимающая отрицательных значений; А, В — точки графика этой функции (рис. 225).
Рис. 225
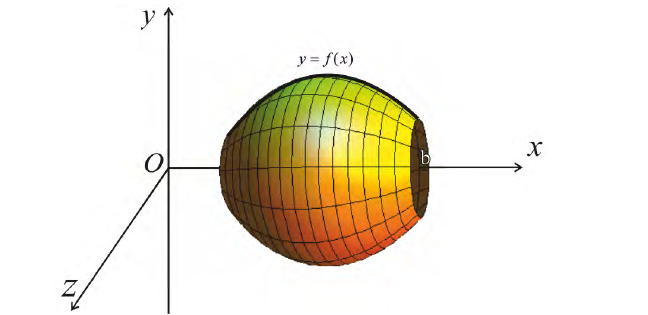
Рассмотрим криволинейную трапецию aABb, ограниченную кривой графика функции y = f(x), отрезками aA, bB и отрезком [a; b] координатной оси Ох (см. рис. 225). При вращении этой трапеции вокруг оси Ох образуется тело вращения (рис. 226), которое обозначим Ф и поставим себе задачу: найти объём этого тела.
Рис. 226
Через произвольную точку х = с (a ⩽ с ⩽ b) отрезка [a; b] проведём плоскость, перпендикулярную оси Ox. Сечением тела Ф этой плоскостью является круг, радиус которого равен f(с), а площадь — πf2(с) (или точка (c; 0)).
Объём части тела Ф, заключённой между этой плоскостью и плоскостью х = a, изменяется при изменении x. Обозначим этот переменный объём V(х). Заметим, что V(x) = V(a) = 0 при х = a; при х = b имеем V(x) = V(b) = V — искомый объём тела вращения Ф.
Покажем, что функция V(x) имеет производную V′(х) и V′(х) = πf2(х).
Придадим абсциссе х приращение ∆х > 0, тогда объём V(х) получает приращение ∆V(х) = V(x + ∆x) – V(x). Пусть m и М — соответственно наименьшее и наибольшее значения функции f(х) на промежутке [х; х + ∆х]. Цилиндр, радиус основания которого равен m, содержится в теле вращения объёма ∆V(x), а цилиндр, радиус основания которого равен M, содержит тело объёма ∆V(х); образующие цилиндров параллельны оси Ох и имеют длину, равную ∆х. Объёмы этих цилиндров равны соответственно πm2•∆x и πM2•∆х. На основании свойства 2 объёмов (п. 10.1) получаем
πm2•∆x ⩽ ∆V(x) ⩽ πM2•∆x,
откуда
πm2 ⩽ 
Рассуждения для случая ∆х < 0 проводятся аналогично и дают тот же результат.
Пусть теперь ∆х 





или
πf2(х) ⩽ 
Значит, 

Таким образом, переменный объём V(x) телa вращения представляет собой одну из первообразных для функции πf 2(х) на отрезке [a; b]. Эта первообразная обладает тем свойством, что при х = a она обращается в нуль (V(a) = 0), а при х = b значение функции V(x) равно объёму тела вращения Ф (V(b) = V).
Если F(х) — также некоторая первообразная для функции πf 2(x), то V(x) = F(x) + С, где С — произвольная постоянная. Так как V (a) = 0, то из равенства V(a) = F (a) + C = 0 находим С = –F(a). Значит, V(x) = F(x) – F(a). Toгдa V(b) = F(b) – F(a). Ho V(b) = V — искомый объём тела вращения Ф. Таким образом, V = F(b) – F(a), где F(b) и F(a) — значения первообразной для функции πf 2(х) соответственно при х = b и х = a. Это означает, что
V = 

Вот почему объём тела, образованного вращением вокруг оси Ох фигуры, ограниченной линиями у = f(x), х = a, х = b, у = 0, вычисляется по формуле
Рис. 227
V = 
ЗАДАЧА. Вычислить объём тела, образованного вращением вокруг оси Ох фигуры, ограниченной линиями у = 
Решение. Воспользуемся формулой V = π

V = π


Ответ: 4π.
1.2. Объёмы конуса, шара и его частей
Используя формулу V = 
а) Объём конуса и усечённого конуса
Теорема 1 (об объёме полного конуса). Объём V конуса с высотой Н и радиусом основания R равен одной трети произведения площади основания на высоту:
V = 
Рис. 228
Доказательство. Конус с высотой Н и радиусом основания R можно рассматривать как тело, образованное вращением вокруг оси Ox прямоугольного треугольника с вершинами О(0; 0), А(Н; 0) и B(Н; R) (рис. 228). Треугольник АОВ является частным случаем криволинейной трапеции, которая ограничена графиком функции у = 
V = 



где πR2 — площадь основания конуса. Теорема доказана. ▼
Теорема 2 (об объёме усечённого конуса). Объём усечённого конуса с высотой Н и радиусами оснований r и R равен сумме объёмов трёх конусов с высотой Н, радиусы оснований которых соответственно равны r, R и 
V = 
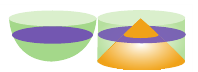
Доказательство. Усечённый конус с высотой H и радиусами оснований r и R можно получить, вращая вокруг оси Oх прямоугольную трапецию OABC, где O(0; 0), A(0; r), В(Н; R), С(H; 0) (рис. 229).

Прямая AВ проходит через точки (0; r) и (Н; R), поэтому её уравнение имеет вид у = 

V = 
Для вычисления интеграла сделаем замену переменных

Тогда 

что и требовалось доказать. ▼
б) Объём шарового слоя
В прямоугольной декартовой системе координат Оху рассмотрим криволинейную трапецию aABb, ограниченную дугой окружности х2 + у2 = R2, –R ⩽ a ⩽ х ⩽ b ⩽ R, отрезком [a; b] оси Ох и отрезками aА и bВ прямых соответственно x = a и х = b (рис. 230, а).

При вращении криволинейной трапеции aАВb вокруг оси Ох образуется шаровой слой (рис. 230, б). Найдём его объём, применяя формулу (*) п. 1.1.
Из уравнения х2 + у2 = R2 имеем у2 = R2 – x2. Поэтому для вычисления объёма V шарового слоя получаем:
Таким образом, объём шарового слоя, отсекаемого от шара x2 + y2 + z2 ⩽ R2 радиуса R плоскостями x = a и x = b, вычисляется пo формуле
V = 
Пусть радиусы оснований шарового слоя равны r1 и r2 (r1 > r2), а высота — H (см. рис. 230, a).
Тогда Н = b – a, 

Формулу (**) преобразуем к виду:
V = 
= 
Из системы равенств (b – a)2 = H2, R2 – a2 = 

R2 – ab = 
Тогда:
V = 
= 
Таким образом, объём шарового слоя с радиусами оснований r1 и r2 и высотой Н вычисляется по формуле
V = 
в) Объём шара
Рис. 231
При вращении полукруга х2 + у2 = R2 (расположенного в плоскости Оху, рис. 231, а) вокруг оси Ох образуется шар радиуса R (рис. 231, б). Из уравнения окружности х2 + y2 = R2 данного полукруга имеем у2 = R2 – х2. Тогда, полагая a = –R, b = R в формуле (*) п. 1.1, находим объём V шара радиуса R:
Vш = 
= 
Таким образом, имеет место следующая теорема.
Теорема 3 (об объёме шара). Объём шара радиуса R вычисляется по формуле
Vш = 
г) Объём шарового сегмента
Если b = R (см. п. 1.2, б), то получаем криволинейную трапецию aAB (рис. 232, а), при вращении которой вокруг оси Ох образуется шаровой сегмент (рис. 232, б).
Рис. 232
Пусть высота шарового сегмента равна Н, тогда a = R – Н. Так как дуга AВ криволинейной трапеции aАВ является частью окружности x2 + y2 = R2 (в плоскости Оxу), то формулу объёма шарового сегмента получим по аналогии с выводом формулы для вычисления объёма шара, учитывая при этом, что пределы a и b интегрирования равны: a = R – H, b = R, т. е.
Vш. сегм = 
=
Таким образом, имеет место следующая теорема.
Теорема 4 (об объёме шарового сегмента). Объём шарового сегмента, отсекаемого от шара радиуса R и имеющего высоту Н, вычисляется по формуле
Vш. сегм =
Если в формуле (***) п. 1.2, б положить r2 = 0, r1 = r, то получим формулу для вычисления объёма шарового сегмента с радиусом основания r и высотой Н:
Vш. сегм = 
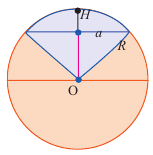
д) Объём шарового сектора
Рис. 233
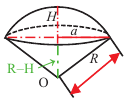
Шаровой сектор состоит из конуса с вершиной в центре шара и шарового сегмента, имеющего с конусом общее основание (риc. 233). Пусть R = ОА — радиус шара; АС = r — радиус основания шарового сегмента, NC = H — его высота; N — точка сферы (рис. 233).
Найдём объёмы конуса и шарового сегмента, учитывая, что высота h конуса равна OC = ON – CN = R – Н.
Объём Vк конуса равен


Выразим r2 через R и H.
B прямоугольном треугольнике AOC находим r2 = AC2 = ОА2 – OC2 = R2 – (R – H)2 = H(2R – H).
Значит,
Vк = 

Для объёма шарового сегмента имеем:
Vш. сегм = 

= 
Тогда для объёма шарового сектора получаем
Vш. сект = Vк + Vш. сегм =
= 


Таким образом, доказана следующая теорема.
Теорема 5 (об объёме шарового сектора). Объём шарового сектора шара радиуса R вычисляется по формуле
Vш. сект = 
где Н — длина высоты шарового сегмента, соответствующего данному шаровому сектору.
В курсе математического анализа, который вам предстоит изучать в высшей школе, будет дано строгое обоснование применения определённого интеграла не только для нахождения объёмов тел, но и для нахождения площадей поверхностей и длин дуг линий. Решите самостоятельно следующие задачи.
1)Найдите объём тела, которое получается при вращении вокруг оси Ох криволинейной трапеции, ограниченной гиперболой у = 
2)Найдите объём тела, образованного вращением вокруг оси Oх фигуры, ограниченной одной полуволной синусоиды у = sin x и отрезком 0 ⩽ х ⩽ π оси абсцисс. (Ответ: 0,5π2.)
3)Найдите объём тела, полученного при вращении кривой у = 0,25х2 вокруг оси Оу в пределах от у = 1 до у = 5. (Ответ: 48π.)
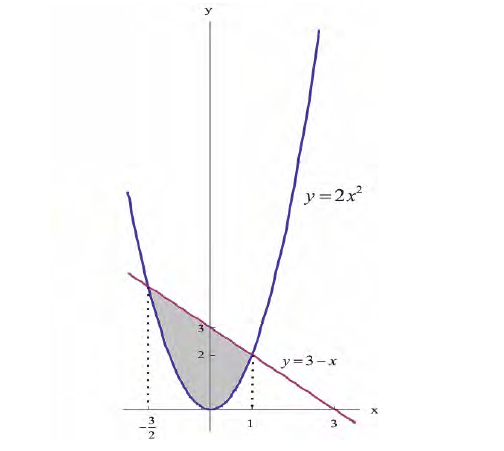
4)Найдите объём тела, образованного вращением вокруг оси Ох фигуры, ограниченной кривыми у = 2х2 и у = x3.
Определение
3. Тело
вращения – это тело, полученное вращением
плоской фигуры вокруг оси, не
пересекающей фигуру и лежащей с ней в
одной плоскости.
Ось вращения может
и пересекать фигуру, если это ось
симметрии фигуры.
Теорема
2. Пусть
криволинейная трапеция, ограниченная
графиком непрерывной неотрицательной
функции
,
осьюи отрезками прямых
и
вращается вокруг оси
.
Тогда объём получающегося тела вращения
можно вычислить по формуле
(2)
Доказательство.
Для такого тела сечение с абсциссой
– это круг радиуса
,
значити формула (1) даёт требуемый результат.
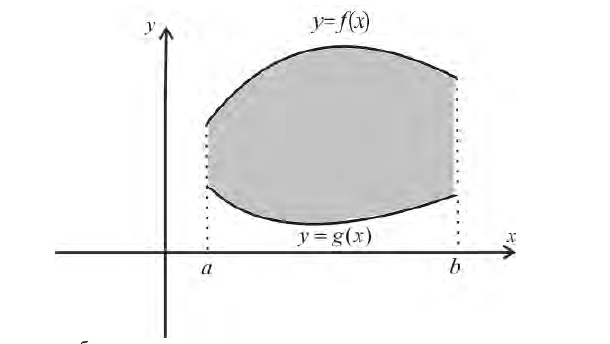
Если фигура
ограничена графиками двух непрерывных
функций
и
,
и отрезками прямыхи
,
причёми
,
то при вращении вокруг оси абсцисс
получим тело, объём которого
Пример
3. Вычислить
объём тора, полученного вращением круга,
ограниченного окружностью вокруг оси абсцисс.
Р
Указанный круг снизу ограничен графиком
функции
,
а сверху –.
Разность квадратов этих функций:
Искомый объём
(графиком
подынтегральной функции является
верхняя полуокружность, поэтому
написанный выше интеграл – это площадь
полукруга).
Пример 4.
Параболический сегмент с основанием
,
и высотой,
вращается вокруг основания. Вычислить
объём получающегося тела («лимон»
Кавальери).
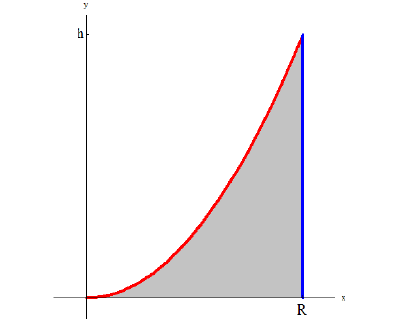
Р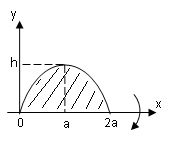
Параболу расположим как показано на
рисунке. Тогда её уравнение
,
причем.
Найдём значение параметра:
.
Итак, искомый объём:
Теорема
3. Пусть
криволинейная трапеция, ограниченная
графиком непрерывной неотрицательной
функции
,
осьюи отрезками прямых
и
,
причём,
вращается вокруг оси.
Тогда объём получающегося тела вращения
может быть найден по формуле
(3)

доказательства.
Разбиваем отрезок
точками
,
на части и проводим прямые.
Вся трапеция разложится на полоски,
которые можно считать приближенно
прямоугольниками с основаниеми высотой
.
Получающийся при
вращении такого прямоугольника цилиндр
разрежем по образующей и развернём.
Получим «почти» параллелепипед с
размерами:
,
и
.
Его объём.
Итак, для объёма тела вращения будем
иметь приближенноё равенство
Для получения
точного равенства надо перейти к пределу
при .
Написанная выше сумма есть интегральная
сумма для функции ,
следовательно, в пределе получим интеграл
из формулы (3). Теорема доказана.
Замечание
1. В теоремах
2 и 3 условие
можно опустить: формула (2) вообще
нечувствительна к знаку,
а в формуле (3) достаточнозаменить на
.
Пример
5.
Параболический сегмент (основание
,
высота)
вращается вокруг высоты. Найти объём
получающегося тела.
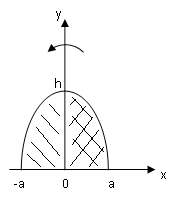
Расположим
параболу как показано на рисунке. И хотя
ось вращения пересекает фигуру, она –
ось – является осью симметрии. Поэтому
надо рассматривать лишь правую половину
сегмента. Уравнение параболы
,
причем,
значит.
Имеем для объёма:
Замечание
2. Если
криволинейная граница криволинейной
трапеции задана параметрическими
уравнениями
,
,
и
,
то можно использовать формулы (2) и (3) с
заменойна
и
на
при измененииt
от
до
.
Пример
6. Фигура
ограничена первой аркой циклоиды
,
,
,
и осью абсцисс. Найти объём тела,
полученного вращением этой фигуры
вокруг: 1) оси;
2) оси.
Решение.
1) Общая формула
В нашем случае:
2) Общая формула
Для нашей фигуры:
Предлагаем
студентам самостоятельно провести все
вычисления.
Замечание
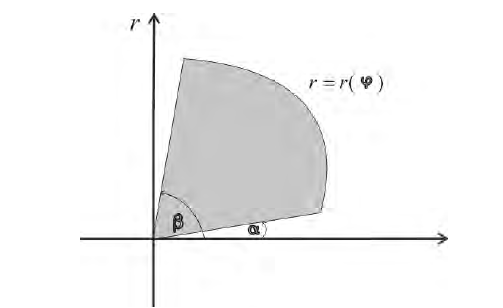
3. Пусть
криволинейный сектор, ограниченный
непре-рывной линией
и лучами
,
,
вращается вокруг полярной оси. Объём
получающегося тела можно вычислить по
формуле.
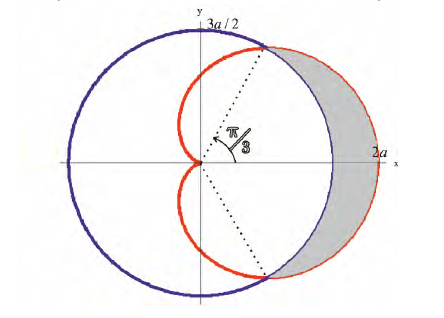
Пример
7. Часть
фигуры, ограниченной кардиоидой
,
лежащая вне окружности,
вращается вокруг полярной оси. Найти
объём тела, которое при этом получается.
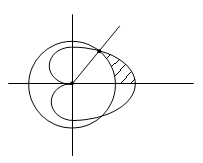
Обе линии, а значит и фигура, которую
они ограничивают, симметричны относительно
полярной оси. Поэтому необходимо
рассматривать лишь ту часть, для которой
.
Кривые пересекаются прии
при
.
Далее, фигуру можно рассматривать как
разность двух секторов, а значит и объём
вычислять как разность двух интегралов.
Имеем:
Задачи
для самостоятельного решения.
1. Круговой сегмент,
основание которого ,
высота
,
вращается вокруг основания. Найти объём
тела вращения.
2. Найти объём
параболоида вращения, основание которого
,
а высота равна.
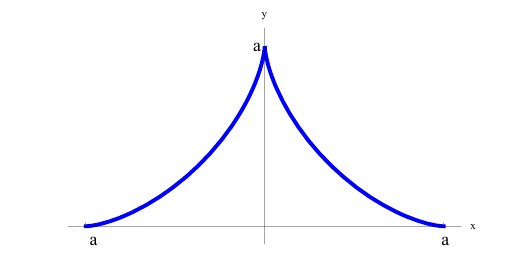
3. Фигура, ограниченная
астроидой
,
вращает-ся вокруг оси абсцисс. Найти
объём тела, которое получается при этом.
4. Фигура, ограниченная
линиями
и
вращается вокруг оси абсцисс. Найти
объём тела вращения.
Соседние файлы в папке Лекции по мат.анализу
- #
- #
- #
- #
- #
- #
- #
Содержание:
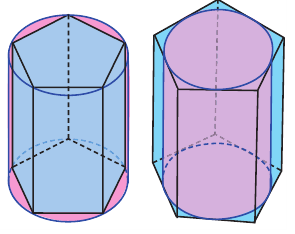
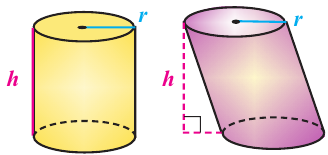
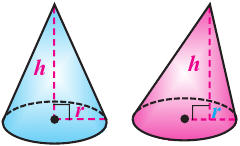
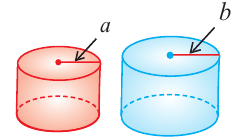
Говоря об объеме, имеют ввиду вместимость пространственной фигуры. Как вы думаете, емкость какого из цилиндров на рисунке больше?
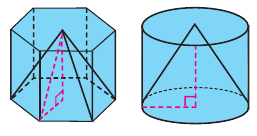
Призмой, вписанной (описанной) в цилиндр, называется призма, основания которой вписаны (описаны) в основания цилиндра.
Объем цилиндра
Пусть в цилиндр с радиусом
При бесконечном возрастании 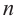
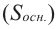
Объем цилиндра равен произведению площади основания на высоту.
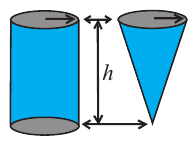
Практическая работа. Какая связь существует между объемами призмы и пирамиды, если они имеют одинаковые высоты и основания? Можно ли эту связь применить для объемов цилиндра и конуса?
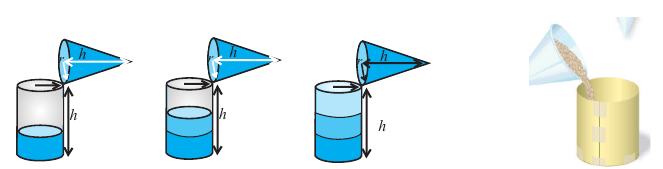
Сделайте из картона модели сосудов в виде конуса и цилиндра, радиусы оснований и высоты которых одинаковы. Заполните цилиндрический сосуд при помощи сосуда в виде конуса (песком, рисом, и т. п.).
Сколько таких сосудов понадобится, чтобы заполнить цилиндрический сосуд? Верно ли утверждение, что цилиндрический сосуд можно заполнить тремя полными сосудами в виде конуса?
Обобщите соответствующую информацию о вычислении объема призмы, цилиндра, пирамиды и конуса, записав ответ в закрашенные ячейки.
Объем призмы и цилиндра:
Объем = площадь основания
Объем пирамиды и конуса:
Объем = 
основание и высоту.
Объем конуса
Объем конуса равен произведению одной третьей площади основания на высоту.
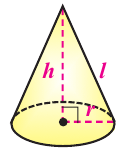
Пример №1
Образующая конуса 9 см, высота 6 см. Найдите объем конуса.
Решение:
Объем шара и его частей
Практическая работа.
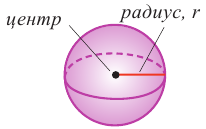
1. Возьмите мяч. Определите его диаметр.
2. Изобразите на бумаге развертку цилиндра, диаметр и высота которого равны диаметру шару.
3. Вырежьте и сверните полученную развертку в цилиндр без верхней крышки. Скрепите развертку при помощи клейкой ленты. Разделите высоту цилиндра на 3 равные части и сделайте соответствующие разметки.
4. Обверните мяч фольгой или плотным материалом и сделайте мешок сферической формы. Наполните его песком.
5. Пересыпьте песок в цилиндр. Какая часть цилиндра заполнится?
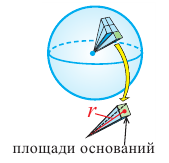
Если разделить поверхность шара сеткой из вертикальных и горизонтальных линий и маленький «прямоугольный» кусочек сферы соединить с центром шара, то можно представить, что шар состоит из множества «маленьких пирамид».
Объем шара можно выразить через сумму объемов «маленьких пирамид» 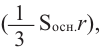
Сумма площадей оснований «маленьких пирамид» будет равна площади поверхности шара. Учитывая, что площадь поверхности шара равна 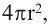
Объем шара:
Объем шара равен произведению 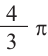
Пример №2
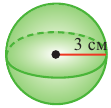
Найдите: а) объем шара радиуса 3 см
b) радиус шара объемом 288
Решение:
а)
b)
Сектор шара и сегмент шара
Шаровой сектор — это часть шара, ограниченная конической поверхностью с вершиной в центре шара. Шаровой сектор-объеденение конуса и шарового сегмента.
Так как шаровой сектор можно рассмотреть как предел суммы объемов маленьких пирамид, вершины которых находятся в центре шара, а основания касаются его поверхности, то
Здесь 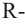
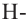
С другой стороны,
Проектная работа.
Отношение между объемами цилиндра, конуса и шара, которое получил Архимед.
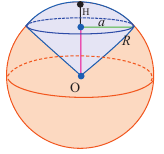
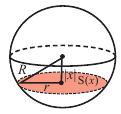
Архимед нашел формулу для нахождения объема шара, исследовав связь между объемом цилиндра, описанного вокруг шара радиуса и объемом конуса, вписанного в данный цилиндр. Попробуйте и вы выполнить это исследование.
Если 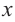
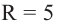
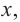
a) Вычислите следующие значения функции
Для примера найдено значение
b) Представьте свои суждения о значениях 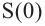
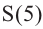
c) Запишите общую формулу для определения площади сечения, расположенного на расстоянии 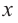
d) Свяжите формулу, полученную в пункте 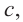
e) Чтобы понять умозаключения Архимеда, вернемся к начальному рисунку.
При «извлечении» конуса из цилиндра в поперечном сечении получаем кольца, параллельные основанию.
На одном и том же уровне поперечное сечение шара является кругом. Из подобия треугольников можно доказать, что площадь кольца каждого слоя равна 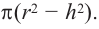
Объемы подобных фигур
Отношения соответствующих линейных размеров подобных пространствнных фигур должны быть равны.
По заданным соответствующим размерам подобных пространственных фигур можно найти неизвестные размеры.
Пример №3
Конусы 
Решение: Запишем отношение линейных размеров: Радиус А Образующая А
Известно, что отношение площадей поверхностей двух подобных пространственных фигур равно квадрату отношения соответствующих линейных размеров или квадрату коэффициента подобия:
Объемы подобных пространственных фигур
Отношение объемов подобных пространственных фигур 
Пример №4
Отношение боковых поверхностей двух подобных цилиндров равно 4:9. Зная, что разность объемов равна 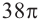
Решение: по условию 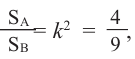
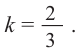
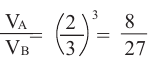
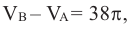
Объемы тел в высшей математике
Под телом Т будем подразумевать ограниченное множество в пространстве.
Будем рассматривать тела, имеющие внутренние точки и границу, которая также принадлежит телу (замкнутые тела), причем такие, что любые две внутренние
точки можно соединить непрерывной линией, проходящей внутри тела.
Определение 1. Рассмотрим тело 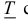
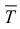
Пусть 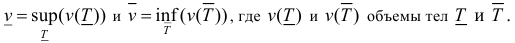
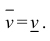
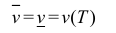
Замечание. Для кубируемости тела Т необходимо и достаточно, чтобы 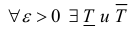
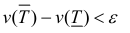
Пусть для кубируемого тела Т известны площади s=s(x) его сечения плоскостями перпендикулярными оси Ох, проходящими через точки (х, 0, 0),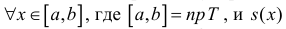
Разобьем отрезок [ a b ] на n частичных отрезков точками 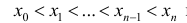
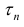
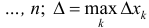
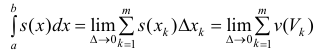
Где 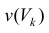
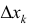
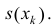
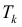
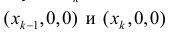
Так как Т – кубируемо, то 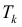
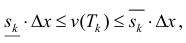
Тогда
∀n ∈ N, или
Где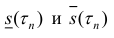
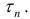
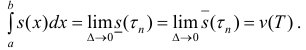
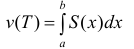
Замечание. Нужно заметить, что неравенство (4), которое использовалось для вывода формулы (6), выполняется, когда любые два рассматриваемые сечения
тела Т при проекции на плоскость yOz полностью содержатся одно в другом.
Однако формула (6) верна и в общем случае. Для этого достаточно потребовать,
чтобы тело Т было кубируемым и функция s (x) – непрерывной.
Пример №5
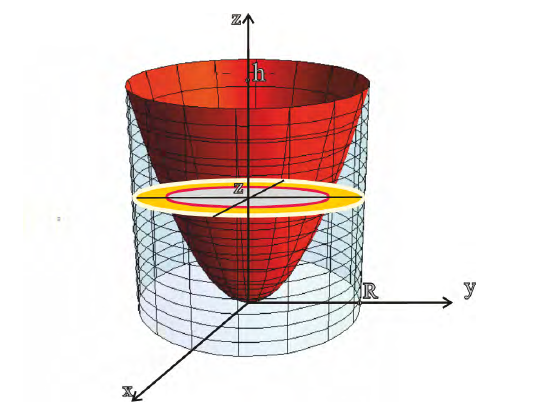
Найти объем тела ограниченного поверхностями 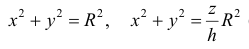
Решение.
Из системы уравнений 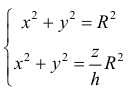
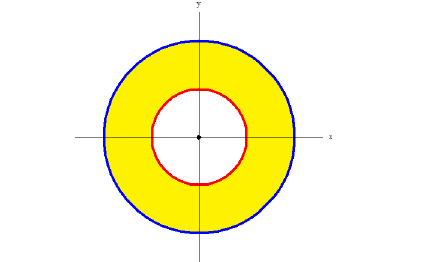
В сечении тела плоскостью проходящей через точку (0, 0, z) перпендикулярно оси Оz получается кольцо
Радиус внешней окружности равен R, радиус внутренней равен
Поэтому по формуле (6):
Формулу (6) удобно применять к телам вращения. Пусть y=f(x) – непрерывна на отрезке 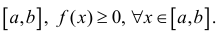
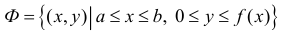
вокруг оси Ох. Получим тело:
Тогда сечением полученного тела плоскостью проходящей через точку (х,0,0) и перпендикулярной оси Ох будет круг радиуса 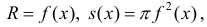
Где y=f(x).
Аналогично, если 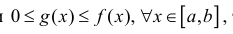
Получим тело, объем которого
Пример №6
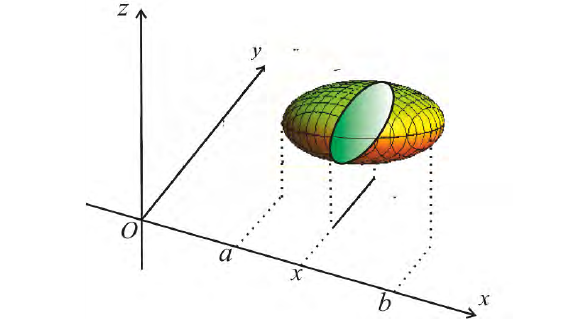
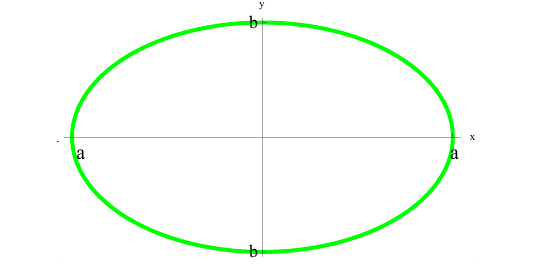
Рассмотрим фигуру Φ ограниченную эллипсом 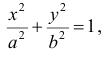
Найдем объем эллипсоида полученного при вращении вокруг оси Ох фигуры Φ .
Решение.
По формуле (7):
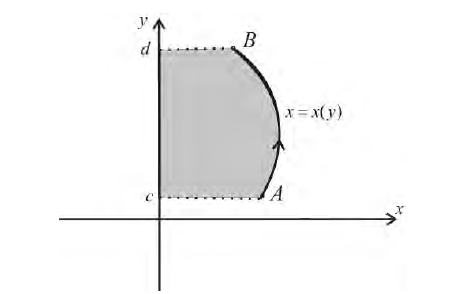
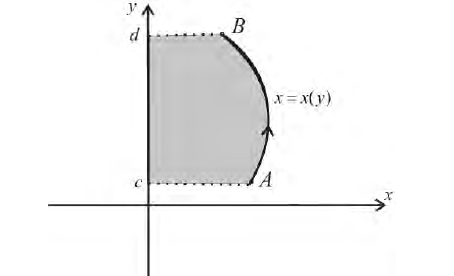
Пусть функция x=x(y) – непрерывна при 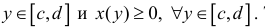
Получим тело, объем которого 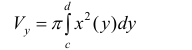
Если же вращать вокруг оси Оу трапецию 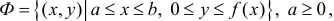
то 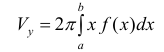
Пример №7
Рассмотрим тело Т из примера 1. Оно получается, если вращать вокруг оси Oz фигуру, ограниченную линиями:
Из первого уравнения найдем 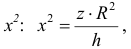
Пример №8
Объем 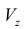
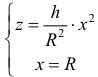
Пример №9
Фигура Ф ограничена линиями 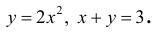
Решение.
Абсциссы точек пересечения: 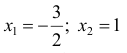
Замечание. Для непрерывной функции 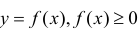
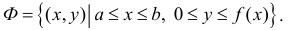
Пусть 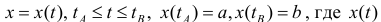
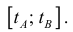
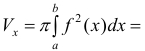
Где 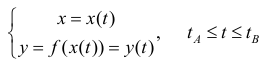
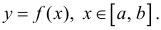
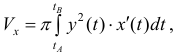
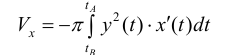
(кривая обходится так, чтобы область Ф оставалась слева).
Аналогично, для непрерывной функции 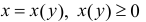
Пусть 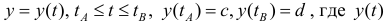
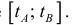
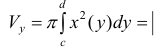
Где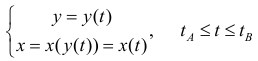
Таким образом 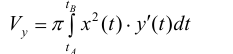
Рассмотрим область ,ограниченную простой замкнутой кривой
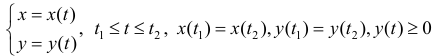

(кривая обходится так, чтобы область оставалась слева).
Аналогично ,для области ограниченной простой замкнутой кривой
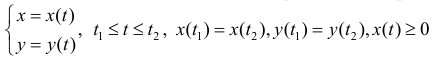
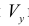
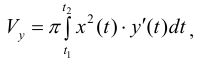
Пример №10
Дана астроида
Найдем 
Решение.
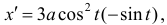
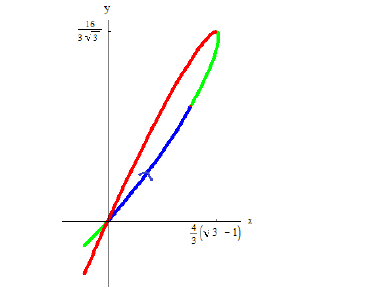
Пример №11
Петля кривой 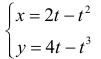

Решение.
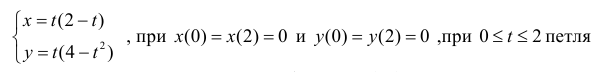
Пусть 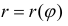
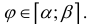
Тогда объем тела при вращении фигуры ϕ вокруг полярной оси равен
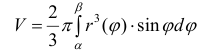
Пример №12
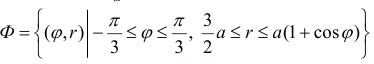
Найдем 
Решение.
По формуле (14):
- Длина дуги кривой
- Геометрические фигуры и их свойства
- Основные фигуры геометрии и их расположение в пространстве
- Пространственные фигуры — виды, изображения, свойства
- Площадь прямоугольника
- Объем пространственных фигур
- Объёмы поверхностей геометрических тел
- Фигуры вращения: цилиндр, конус, шар
Для того, чтобы найти объем фигуры, образованной вращением вокруг оси Ox нужно вычислить определенный интеграл от квадрата функции, задающей график и умножить на число Пи.
$$ V = pi int_a^b y^2 dx $$
В формуле $ a $ и $ b $ значения отложены по оси Ox. Фукция $ y (x) $ задаёт график фигуры, объем вращения которой необходимо вычислить.
- Строим график фигуры
- Вычисляем определенный интеграл
| Пример 1 |
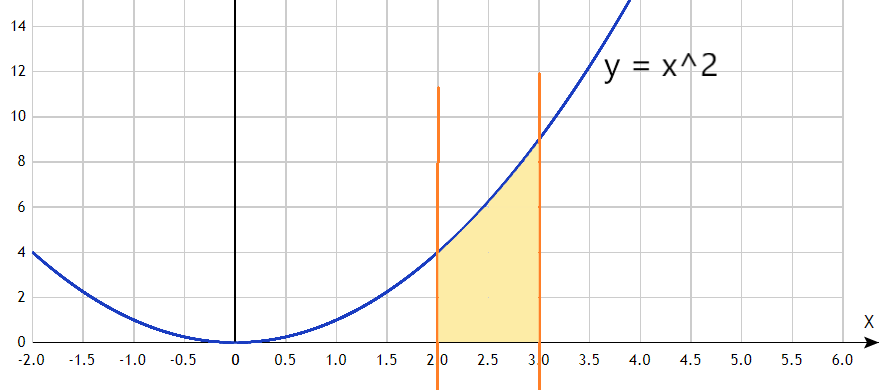
| Вычислить объем тела вращения вокруг оси Ox: $ y = x^2 $ и $ a = 2, b = 3 $ |
| Решение |
|
Выполняем построение графика. Чертим на плоскости параболу $ y = x^2 $. Выставляем на чертеже оранжевые линии, соответствующие ограничениям $ a = 2, b = 3 $. Закрашиваемая область желтым цветом выделяет фигуру, объем вращения которой будем искать. Подставляем в формулу функцию $ y = x^2 $ и пределы интегрирования. Вычисляем определенный интеграл $$ V = pi int_2^3 (x^2)^2 dx = pi int_2^3 x^4 dx = $$ Для взятия интеграла воспользуемся формулой $ int x^p dx = frac{x^{p+1}}{p+1} $ $$ = pi frac{x^5}{5} bigg |_2^3 = pi frac{243}{5} — pi frac{32}{5} = frac{211}{5} pi = 132.5 $$ Получили объем фигуры $ V = 132.5 $ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$ V = 132.5 $$ |
| Пример 2 |
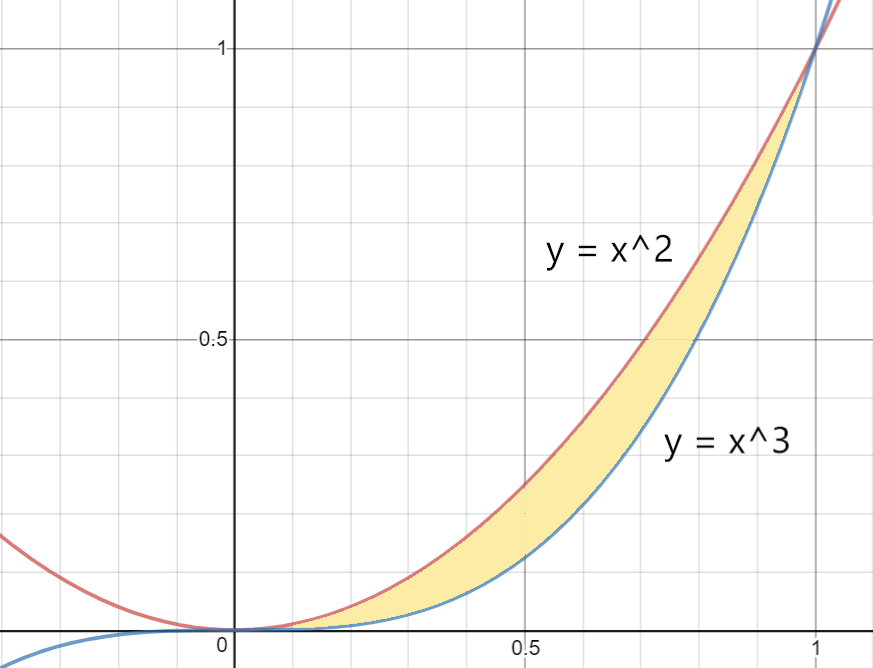
| Найти объем тела вращения фигуры вокруг оси Ox, заданной двумя функциями $$ y = x^2, y = x^3 $$ |
| Решение |
|
В данном примере необходимо найти точки пересечения двух графиков функций. Приравниваем их друг к другу и решаем уравнение относительно одной переменной $ x $: $$ x^2 = x^3 $$ Переносим всё в одну строну $$ x^3 — x^2 = 0 $$ Выносим за скобку неизвестную $ x^2 $ и получаем корни уравнения: $$ x^2(x-1) = 0 $$ $$ x^2 = 0, x-1=0 $$ $$ x_1=0, x_2=1 $$ Выполняем построение графиков функций для наглядности. На рисунке закрашиваем область, ограниченную двумя функциями. Для того, чтобы найти объем тела вращения, заданного с помощью двух функций, необходимо воспользоваться идеей разности объемов. А имеенно, находим сначала объем фигуры вращения, заданной функцией $ y = x^2 $, затем отдельно $ y = x^3 $. $$ V_1 = pi int_0^1 (x^2)^2 dx = pi frac{x^5}{5} bigg |_0^1 = frac{pi}{5} $$ $$ V_2 = pi int_0^1 (x^3)^2 dx = pi frac{x^7}{7} bigg |_0^1 = frac{pi}{7} $$ Получаем искомый объем с помощью разности объемов $$ V = V_1 — V_2 = frac{pi}{5} — frac{pi}{7} = frac{2pi}{35} $$ |
| Ответ |
| $$ V = frac{2pi}{35} $$ |