Как найти объем части шестиугольной призмы

Определение объемов геометрических тел является одной из важных задач пространственной геометрии. В данной статье рассматривается вопрос, что такое призма с шестиугольным основанием, а также приводится формула объема правильной шестиугольной призмы.

Определение призмы

С точки зрения геометрии призмой называется фигура в пространстве, которая образована двумя одинаковыми многоугольниками, расположенными в параллельных плоскостях. А также несколькими параллелограммами, которые эти многоугольники соединяют в единую фигуру.

В трехмерном пространстве призму произвольной формы можно получить, если взять любой многоугольник и отрезок. Причем последний плоскости многоугольника принадлежать не будет. Тогда, располагая этот отрезок от каждой вершины многоугольника, можно получить параллельный перенос последнего в другую плоскость. Образованная таким способом фигура будет призмой.

Чтобы иметь наглядное представление о рассматриваемом классе фигур, приведем рисунок четырехугольной призмы.

Многие знают эту фигуру под названием параллелепипеда. Видно, что два одинаковых многоугольника призмы представляют собой квадраты. Их называют основаниями фигуры. Остальные четыре ее стороны — прямоугольники, то есть это частный случай параллелограммов.

Шестиугольная призма: определение и виды

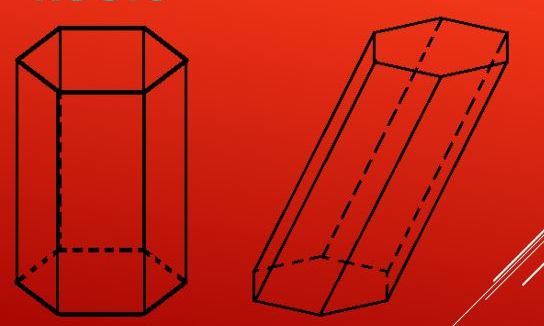
Прежде чем приводить формулу, как определяется объем шестиугольной правильной призмы, необходимо четко понять, о какой фигуре пойдет речь. Шестиугольная призма имеет в основаниях шестиугольник. То есть, плоский многоугольник с шестью сторонами, углов столько же. Боковые стороны фигуры так же, как и для любой призмы, в общем случае являются параллелограммами. Сразу отметим, что шестиугольное основание может быть представлено как правильным, так и неправильным шестиугольником.

Расстояние между основаниями фигуры — это ее высота. Далее мы будем обозначать ее буквой h. Геометрически высота h представляет собой отрезок, перпендикулярный обоим основаниям. Если этот перпендикуляр:

• опущен с геометрического центра одного из оснований;
• пересекает второе основание также в геометрическом центре.

Фигура в этом случае называется прямой. В любом другом случае призма будет косоугольной или наклонной. Разницу между этими видами шестиугольной призмы можно увидеть с первого взгляда.

Прямая шестиугольная призма — это фигура, имеющая в основании правильные шестиугольники. При этом она является прямой. Рассмотрим подробнее ее свойства.

Элементы правильной шестиугольной призмы

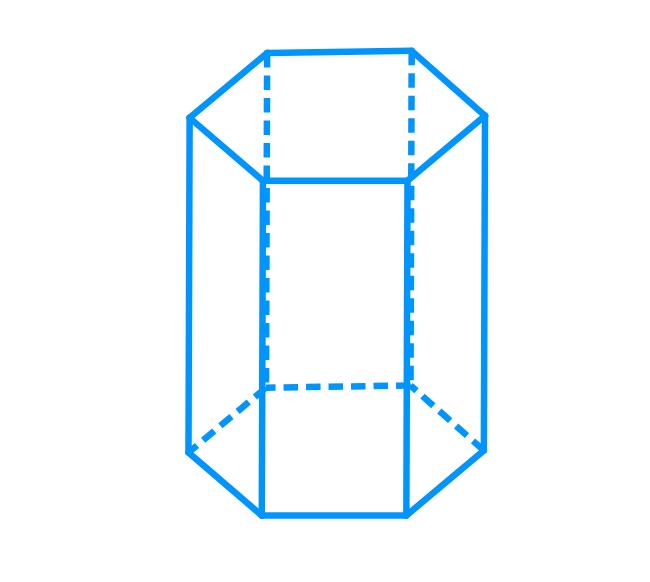
Чтобы понять, как вычислить объем правильной шестиугольной призмы (формула приведена ниже в статье), необходимо также разобраться, из каких элементов состоит фигура, а также какими свойствами она обладает. Чтобы было легче анализировать фигуру, покажем ее на рисунке.

Главными ее элементами являются грани, ребра и вершины. Количества этих элементов подчиняется теореме Эйлера. Если обозначить Р — число ребер, В — количество вершин и Г — граней, тогда можно записать равенство:

Р = Г + В — 2.

Проверим его. Число граней рассматриваемой фигуры равно 8. Две из них — это правильные шестиугольники. Шесть граней представляет собой прямоугольники, это видно из рисунка. Число вершин составляет 12. Действительно, 6 вершин принадлежат одному основанию, и 6 другому. Согласно формуле, число ребер должно равняться 18, что является справедливым. 12 ребер лежат в основаниях и 6 образуют параллельные друг другу стороны прямоугольников.

Переходя к получению формулы объема правильной шестиугольной призмы, следует остановить свое внимание на одном важном свойстве этой фигуры: прямоугольники, образующие боковую поверхность, равны между собой и перпендикулярны обоим основаниям. Это приводит к двум важным следствиям:

1. Высота фигуры равна длине ее бокового ребра.
2. Любое сечение боковой поверхности пирамиды, выполненное с помощью секущей плоскости, которая параллельна основаниям, является правильным шестиугольником, равным этим основаниям.

Площадь шестиугольника

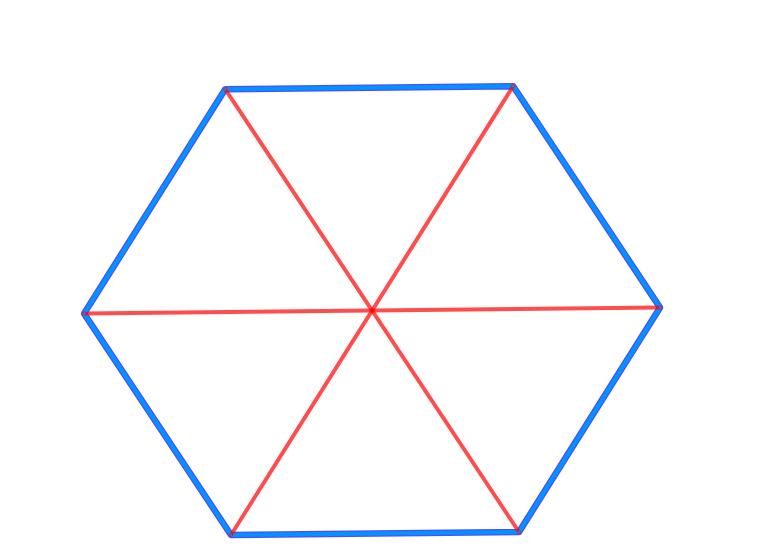
Можно интуитивно догадаться, что эта площадь основания фигуры появится в формуле объема правильной призмы шестиугольной. Поэтому в данном пункте статьи найдем эту площадь. Правильный шестиугольник, разделенный на 6 одинаковых треугольников, вершины которых пересекаются в его геометрическом центре, показан ниже:

Каждый из этих треугольников является равносторонним. Доказать это не очень сложно. Поскольку вся окружность имеет 360^o, то углы треугольников вблизи геометрического центра шестиугольника равны 360^o/6=60^o. Расстояния от геометрического центра до вершин шестиугольника являются одинаковыми.

Последнее означает, что все 6 треугольников будут равнобедренными. Поскольку один из углов равнобедренных треугольников равен 60^o, значит, два остальных угла тоже равны по 60^o. ((180^o-60^o)/2) — треугольники равносторонние.

Обозначим длину стороны шестиугольника буквой a. Тогда площадь одного треугольника будет равна:

S₁ = 1/2*√3/2*a*a = √3/4*a².

Формула получена на основании стандартного выражения для площади треугольника. Тогда площадь S₆ для шестиугольника будет:

S₆ = 6*S₁ = 6*√3/4*a² = 3*√3/2*a².

Формула определения объема правильной шестиугольной призмы

Чтобы записать формулу для объема рассматриваемой фигуры, следует учесть приведенную выше информацию. Для произвольной призмы объем пространства, ограниченный ее гранями, вычисляется так:

V = h*S_o.

То есть, V равен произведению площади основания S_o на высоту h. Поскольку мы знаем, что высота h равна длине бокового ребра b для шестиугольной правильной призмы, а площадь ее основания соответствует S₆, то формула объема правильной шестиугольной призмы примет вид:

V₆ = 3*√3/2*a²*b.

Пример решения геометрической задачи

Дана шестиугольная правильная призма. Известно, что она вписана в цилиндр радиусом 10 см. Высота призмы в два раза больше стороны ее основания. Необходимо найти объем фигуры.

Чтобы найти требуемую величину, необходимо знать длину стороны и бокового ребра. При рассмотрении правильного шестиугольника было показано, что его геометрический центр расположен в середине описанной вокруг него окружности. Радиус последней равен расстоянию от центра до любой из вершин. То есть он равен длине стороны шестиугольника. Эти рассуждения приводят к следующим результатам:

a = r = 10 см;

b = h = 2*a = 20 см.

Подставляя эти данные в формулу объема правильной шестиугольной призмы, получим ответ: V₆≈5196 см³ или около 5,2 литра.

Рассмотрением свойств и особенностей правильных фигур в трехмерном пространстве занимается стереометрия. Одним из многочисленных классов объемных фигур являются призмы. В данной статье приведем формулу объема призмы шестиугольной и покажем, как ее следует использовать при решении задачи.

Что такое шестиугольная призма?

Коротко отвечая на поставленный вопрос, следует сказать, что любая призма, имеющая в основании плоский многоугольник с шестью углами и шестью сторонами, называется шестиугольной. Этот многоугольник называется основанием фигуры. Рисунок ниже показывает, как выглядит такая призма.

Видно, что фигура образована двумя одинаковыми шестиугольными основаниями, которые расположены в параллельных плоскостях. Соединены они с помощью шести параллелограммов. Призма имеет 8 граней, 18 ребер и 12 вершин.

Если все параллелограммы, которые образуют боковую поверхность, представляют собой прямоугольники или квадраты, то фигура будет прямой. У прямой призмы расстояние между основаниями (высота) совпадает с длиной бокового ребра. Если основания прямой фигуры являются равносторонними и равноугольными, то можно говорить о правильной шестиугольной призме.

Определение объема

Теперь ответим на вопрос, как найти объем призмы шестиугольной. Формула для объем произвольной призмы имеет следующий вид:

V = S_o*h

Где S_o — площадь основания, h — высота фигуры. Если мы имеем правильную призму с шестиугольником в основании, то его площадь рассчитать можно, пользуясь следующим выражением:

S_o = 3*√3/2*a²

Где латинской буквой a обозначена длина ребра основания. Это выражение можно получить самостоятельно, если разделить правильный шестиугольник на шесть одинаковых равносторонних треугольников, а затем сложить их площади. Длины сторон треугольников при таком делении будут равны a.

Учитывая выражение для S_o, можно привести формулу объема призмы шестиугольной правильной. Она будет иметь такой вид:

V = 3*√3/2*a²*h

Выражение показывает, что для определения величины V правильной призмы достаточно знать всего два ее линейных размера.

Если в основании прямой фигуры будет находиться неправильный шестиугольник, тогда следует применить геометрический анализ, чтобы определить его площадь S_o.

Самым сложным случаем определения объема шестиугольной призмы является ситуация с наклонной фигурой. Для нее высота уже не равна длине бокового ребра. Чтобы ее вычислить, следует знать какой-либо вертикальный угол (либо между основанием и боковой гранью, либо между ребрами боковым и основания).

Пример задачи

Дана правильная призма шестиугольная. Известно, что ее самая длинная объемная диагональ составляет 25 см. Угол между ней и плоскостью основания составляет 30^o. Чему равен объем геометрической фигуры?

Чтобы воспользоваться полученной выше формулой объема призмы шестиугольной, следует вычислить параметры a и h. Самая длинная объемная диагональ соединяет противоположные вершины разных оснований. Знание ее длины и угла между ней и основанием позволяет вычислить высоту и длину ребра шестиугольника с помощью следующих формул:

a = 25*cos(30^o)/2 = 10,825 см;

h = 25*sin(30^o) = 12,5 см

Теперь можно вычислить V:

V = 3*√3/2*a²*h = 3*√3/2*10,825²*12,5 = 3805,55 см³

Таким образом, искомый объем равен приблизительно 3,8 литра.

Все фигуры, которые ограничены гранями, находящимися в разных плоскостях в пространстве, обладают некоторым объемом. Вычислением этой величины занимается специальный геометрический раздел — стереометрия. В данной статье приведем формулу объема шестиугольной призмы.

Что такое призма?

Очевидно, что прежде чем находить объем геометрической фигуры, следует познакомиться с ней и понять, какими свойствами она обладает. В данном случае речь идет о призме. В стереометрии для этой фигуры приводится следующее определение: призмой называется любой пространственный геометрический объект, который ограничен двумя n-угольниками, находящимися в параллельных плоскостях, и n параллелограммами. Здесь n — любое натуральное число начиная с трех.

Вам будет интересно:Структурный гетерохроматин — это что такое?

Построить фигуру несложно. Для этого следует взять произвольный многоугольник и с помощью одинаковых параллельных друг другу отрезков перенести его в другую плоскость. Получившаяся фигура будет призмой. Отметим, что она, в отличие от конуса, цилиндра и сферы, не является фигурой вращения, то есть ее нельзя получить с помощью вращения вокруг оси какой-либо плоской фигуры.

Вам будет интересно:Социально-значимая деятельность: определение, особенности, развитие и примеры

Выше на рисунке приведен для примера параллелепипед, который является четырехугольной призмой.

Призма шестиугольная и ее виды

Далее в статье приведем формулу объема призмы шестиугольной. Что представляет собой эта фигура? Любая призма, имеющая в основании шестиугольник, называется шестиугольной.

Она образована двумя шестиугольниками в основаниях и шестью параллелограммами, совокупность которых составляет боковую площадь фигуры. Эта призма имеет 12 вершин, 8 граней или сторон и 18 ребер, 2/3 из которых принадлежат основаниям.

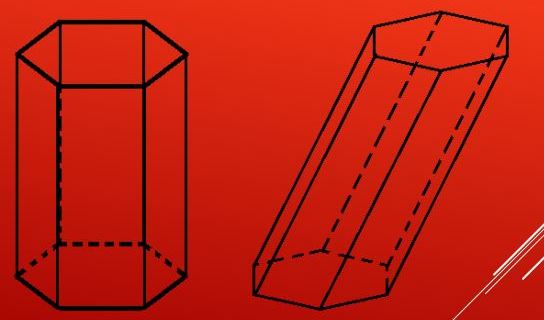
Приведенному описанию элементов соответствуют несколько видов шестиугольной призмы. Во-первых, эта фигура может быть выпуклой или вогнутой, что зависит от шестиугольника в основаниях, во-вторых, призма может быть наклонной и прямой. Разница между ними заключается в том, что в прямой фигуре любая боковая сторона будет перпендикулярна основаниям, а в наклонной фигуре боковые стороны пересекают основания под некоторыми углами, которые отличны от 90o. Обе призмы показаны на рисунке.

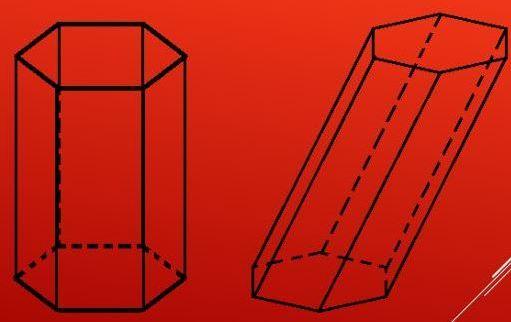
Заметим, что условие перпендикулярности боковых сторон и оснований приводит к тому, что параллелограммы прямой призмы становятся прямоугольниками.

Наконец, в-третьих, шестиугольная призма бывает правильной и неправильной. Последней будет любая фигура, которая не является прямой и не обладает правильным шестиугольным основанием. Далее основное внимание будем уделять именно правильной призме.

Правильный шестиугольник

Для определения объемов геометрических фигур многих классов необходимо знать значение площади их основания. Этот факт справедлив для пирамид, цилиндров, конусов. Призмы тоже не являются исключением.

Чтобы найти площадь основания шестиугольной призмы, следует рассчитать площадь шестиугольника. Проще всего сделать это для правильной фигуры. Для наглядности покажем, что такое правильный шестиугольник.

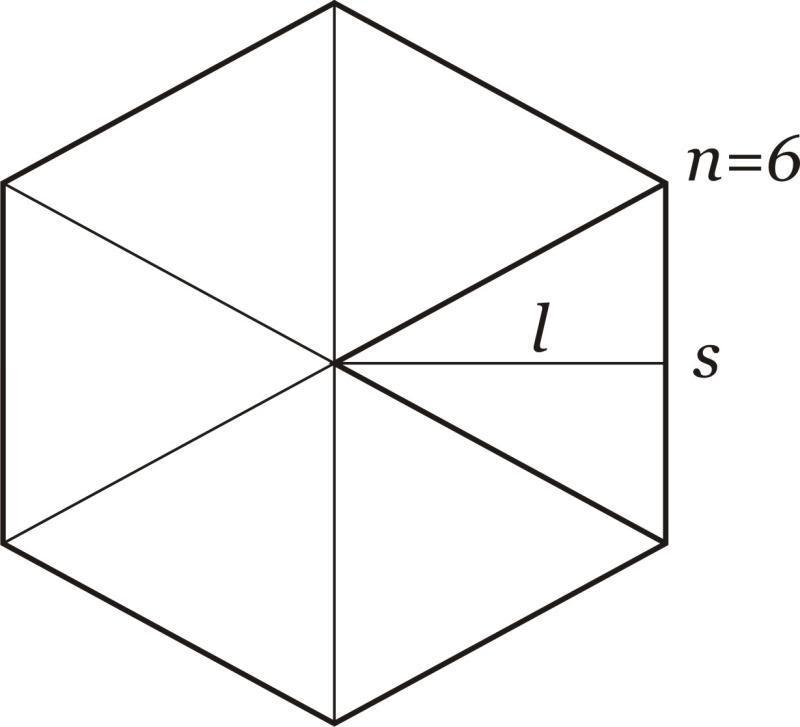
Видно, что представляет он многоугольник, образованный шестью одинаковыми сторонами, которые пересекаются под углами 120o. Также видно, что в шестиугольник можно вписать окружность некоторого радиуса, а также можно описать его окружностью.

Вычисление площади основания призмы шестиугольной правильной сводится к определению площади приведенной выше фигуры. Если шестиугольник разбить на равносторонние треугольники так, как показано на рисунке, то его площадь будет равна умноженной на 6 площади одного треугольника. Обозначим длину стороны шестиугольника буквой a, тогда для площади S шестиугольника получаем:

S = 6*1/2*a*√3/2*a = 3*√3/2*a2.

Для любого другого шестиугольника, который не является правильным, эта формула будет несправедливой.

Формула объема шестиугольной призмы

Вычислить объем любой призмы несложно, для этого следует знать всего два ее параметра: высоту h и основания площадь S. Расчет объема V осуществляется по следующей формуле:

V = h*S.

Отметим важную вещь: записанное выражение справедливо для любых видов призм, включая вогнутые и наклонные. Тем не менее для произвольной призмы, несмотря на простоту формулы, применять ее бывает сложно. Сложность связана с определением обоих параметров в выражении.

В связи с вышесказанным, рассмотрим конкретную правильную призму с правильным шестиугольным основанием. Если ее высота равна h, а длина стороны равна a, тогда формула объема шестиугольной призмы правильной примет вид:

V = 3*√3/2*h*a2.

При записи этого выражения была подставлена формула для S, приведенная в предыдущем пункте.

Далее решим две задачи, в которых покажем, как найти объем шестиугольной призмы для конкретных случаев.

Задача с известной диагональю

Ниже на рисунке показана правильная призма. Известно, что сторона ее основания равна 9 см. Чему равен объем шестиугольной призмы, если диагональ AB имеет длину 21 см.

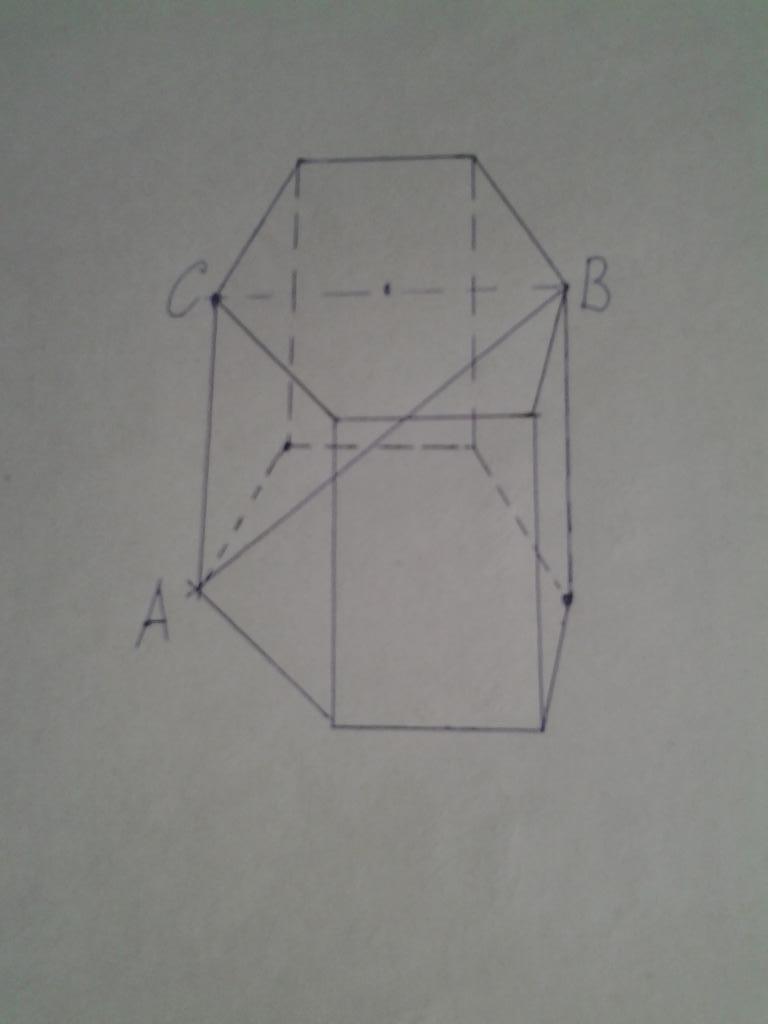
Не сложно догадаться, взглянув на рисунок, что треугольник ABC является прямоугольным, причем сторона AB — это гипотенуза. Катет AC является высотой h фигуры. Чтобы вычислить объем призмы, нам необходимо найти длину этого катета. Заметим, что второй катет CB имеет в два раза большую длину, чем сторона основания, то есть 18 см. Применяем теорему Пифагора и получаем:

h = AC = √(AB2-CB2) = √(212-182) ≈ 10,82 см.

Значение высоты мы округлили до сотых долей сантиметра.

Поскольку нам известна высота h и сторона основания a, то можно применить формулу для V. Получаем:

V = 3*√3/2*h*a2 = 3*√3/2*10,82*92 = 2277 см3.

Таким образом, рассмотренная призма имеет объем почти 2,3 литра.

Задача с вписанным в призму цилиндром

Известно, что цилиндр с радиусом 12 см вписан в правильную шестиугольную призму. Объем цилиндра равен 1360 см3. Чему равен объем призмы?

Как было показано, определить объем призмы можно, если знать ее высоту и сторону основания. Начнем с определения стороны. Поскольку радиус r окружности, вписанной в шестиугольник, известен, значит, длину стороны a можно рассчитать так:

a = 2*r/√3.

Понять, откуда взялась эта формула, можно, если учесть, что радиус r является высотой одного из шести равносторонних треугольников шестиугольника.

Теперь вычислим высоту h призмы. Согласно условию задачи, она должна совпадать с высотой цилиндра. Объем же цилиндра рассчитывается по той же формуле, что и для призмы. Имеем:

Vc = So*h = pi*r2*h =>

h = Vc/(pi*r2).

Подставляем выражения для a и h в формулу для V призмы, получаем:

V = 3*√3/2*h*a2 = 3*√3/2*Vc/(pi*r2)*(2*r/√3)**2 = 2*√3*Vc/pi.

Мы пришли к интересному результату: оказывается, объем шестиугольной призмы не зависит от радиуса вписанного цилиндра, а однозначно определяется его объемом. Подставив значение Vc, получаем объем призмы, равный приблизительно 1500 см3.

A hexagonal prism is a three-dimensional geometric structure with two hexagonal bases connected by six rectangular faces. It is a polyhedron with eight faces, twelve vertices, and eighteen edges. It is also known as an octahedron as it has eight faces; two of the eight faces are hexagons, which are the bases of the prism, and the other six faces are rectangles, which are the lateral (or) side faces of the prism. The top and bottom faces of the hexagonal prism are in the shape of a hexagon and are congruent with each other. 

There are two kinds of hexagonal prisms, namely, a regular hexagonal prism and an irregular hexagonal prism.

• A regular hexagonal prism is a prism that has two hexagonal bases whose all sides are of the same length. In a regular hexagonal prism, the angles also measure the same.
• An irregular hexagonal prism is a prism that has two irregular hexagonal bases. All the sides of the base do not have the same length, and the measures of each angle are different.

Surface Area of a Hexagonal Prism

The total area that is covered by the surfaces of a hexagonal prism is referred to as its surface area. The surface area of a prism is measured in terms of square units such as sq. m, sq. cm, sq. in, etc. A hexagonal prism has two types of areas just like other three-dimensional shapes: lateral surface area (LSA) and total surface area (TSA).

Let us consider a hexagonal prism that has an apothem length “a”, a base length “s”, and a height “h”. We know that the general formula to calculate the lateral surface area of a prism is the product of its base and height. So, the lateral surface area of the prism of a hexagonal prism is determined by calculating the product of the perimeter of the base of the hexagonal prism and its height.

The formula to determine the lateral surface area of the hexagonal prism is equal to the sum of the areas of its six rectangular faces. Thus, 

Lateral surface area of hexagonal prism (LSA) = 6sh sq. units.

Where “s” is the length of the base edge, and
“h” is the height of the prism.

The formula to determine the surface area of a hexagonal prism is given as follows:

Total Surface Area, TSA = 2×(Area of hexagonal base) + 6×(Area of rectangular faces) = 6s(a + h).

Total surface area of the hexagonal prism (TSA) = 6s(a + h) sq. units.

Where “a” is the apothem length,
“s” is the length of the base edge, and
“h” is the height of the prism.

The formula to determine the surface area of a hexagonal prism in the case of a regular hexagonal prism, TSA = 6sh + 3√3s².

Total surface area of the hexagonal prism (TSA) = 6sh + 3√3s² sq. units.

Where “s” is the length of the base edge, and
“h” is the height of the prism.

Volume of a Hexagonal Prism

The volume of a hexagonal prism is the amount of space enclosed by it in three-dimensional space. It is also referred to as the amount of substance that it can hold, which is the capacity of a hexagonal prism. The formula for the volume of a hexagonal prism is equivalent to the product of its base area and height, which is measured in terms of cubic units such as cm³, m³, in³, etc.

The formula for finding the volume of a hexagonal prism is given as follows,

Volume of the Hexagonal Prism (V) = Base area × height

The formula for calculating the volume of a hexagonal prism when the length of the edge of the base and height of the prism is known is given as follows.

Volume of the Hexagonal Prism (V) = [(3√3)/2]s²h

Where “s” is the length of the base edge, and
“h” is the height of the prism.

The formula for calculating the volume of a hexagonal prism when the apothem length, length of the edge of the base, and height of the prism are known is given as follows.

Volume of the Hexagonal Prism (V) = 3ash

Where “a” is the apothem length,
“s” is the length of the base edge, and
“h” is the height of the prism.

Solved Example on Volume of a Hexagonal Prism

Example 1: Calculate the volume of a hexagonal prism with a base edge length of 15 cm and a height of 12 cm.

Solution:

Given data, 

Length of the base edge (s) = 15 cm

The height of the prism (h) = 12 cm

We know that,

The volume of a hexagonal prism = [(3√3)/2]s²h

= (3/2) × (1.732) × (15)² × 12

= 7,014.805 cu. cm

Hence, the volume of the hexagonal prism is 7,014.805 cu. cm.

Example 2: Determine the volume of the hexagonal prism if its height is 10 inches and its base area is given as 60 sq. in.

Solution:

Given data, 

Base area = 60 sq. in

The height of the prism (h) = 10 inches

We know that

The volume of the hexagonal prism (V) = Base area × height

= 60 × 10 = 600 cu. in

Hence, the volume of the hexagonal prism is 600 cu. in.

Example 3: Calculate the volume of a hexagonal prism if its height is 13 cm, the length of each side of the base is 10 cm, and the apothem length is 8 cm.

Solution:

Given data,

Length of the base edge length (s) = 10 cm

Apothem length (a) = 8 cm

The height of the prism (h) = 13 cm

We know that

The volume of the hexagonal prism (V) = 3ash cubic units

= 3 × 8 × 10 × 13 = 3,120 cu. cm

Hence, the volume of the hexagonal prism is 3,120 cu. cm.

Example 4: Find the total surface area of a hexagonal prism if the length of each side of the base is 8 cm and the height is 10 cm.

Solution:

Given data,

Length of the base edge (s) = 8 cm

The height of the prism (h) = 10 cm

We know that,

The total surface area of the hexagonal prism = 6sh + 3√3s²

= 6 × 8 × 10 + 3√3 × (8)²

= 480 + 3√3 × 64

= 480 + 332.554 = 812.554 sq. cm

Thus, the total surface area of the hexagonal prism is 812.554 sq. cm.

Example 5: Determine the lateral surface area of a hexagonal prism with a base edge length of 12 cm and a height of 9 cm.

Solution:

Given data,

Length of the base edge length (s) = 12 cm

The height of the prism (h) = 9 cm

We know that,

The lateral surface area of a hexagonal prism = 6sh sq. units

LSA = 6 × 12 × 9

LSA = 648 sq. cm

Hence, the volume of the hexagonal prism is 648 sq. cm.

FAQs on Hexagonal Prism

Question 1: What is the Volume of a Hexagonal Prism?

Answer:

The volume of a hexagonal prism is the amount of space enclosed by it in three-dimensional space. It is also referred to as the amount of substance that it can hold, which is the capacity of a hexagonal prism. The formula for the volume of a hexagonal prism is equivalent to the product of its base area and height, which is measured in terms of cubic units such as cm³, m³, in³, etc.

The formula for finding the volume of a rectangular prism is given as follows,

The volume of the hexagonal prism (V) = Base area × height

Question 2: How to determine the Volume of a Hexagonal Prism?

Answer:

Follow the steps given below to determine the volume of a hexagonal prism:

Step 1: Calculate the base area of the prism using the appropriate formula.
Step 2: Note down the value of the height of the given hexagonal prism.
Step 3: Substitute the values of the given dimensions in the formula, V = [(3√3)/2]s²h
Step 4: Finally, write the final value in appropriate cubic units.

Question 3: How can we determine the Volume of a Hexagonal Prism when its Base Area and Height are given?

Answer:

We know that the general formula for calculating the volume of any prism is the product of its base area and its height. A hexagonal prism is a prism that has a hexagon as its base. So, we can also use the same formula for determining the volume of a hexagonal prism. As both the base area and the height of the hexagonal prism are given, the formula to determine the volume of a hexagonal prism is given as follows:

Volume of a hexagonal prism = Base Area × height.

Question 4: What will happen to the Volume of the Hexagonal Prism if its Height is reduced to Half?

Answer:

We know that the formula for calculating the volume of the hexagonal prism is V = 3abh. Where “a” is the apothem length, “s” is the length of the base edge, and “h” is the height of the prism. So, the volume of the prism is directly proportional to its height. So, if the height is reduced to half, the new height will become (h/2). So, the volume of the new hexagonal prism will be 3ab (h/2) = (1/2) (3abh) = V/2. Therefore, we can conclude the volume will also be reduced by half.

Question 5: What is meant by the Surface Area of a Hexagonal Prism?

Answer:

The total area that is covered by the surfaces of a hexagonal prism is referred to as its surface area. The surface area of a prism is measured in terms of square units such as sq. m, sq. cm, sq. in, etc. The formula to determine the surface area of a hexagonal prism is given as follows:

Total Surface Area, TSA = 2(Area of hexagon base) + 6(Area of rectangle faces) = 6s(a + h), where the “a” is apothem length of the prism, “s” is the length of the base edge, and “h” is the height of the prism. 

The formula to determine the surface area of a hexagonal prism in the case of a regular hexagonal prism, TSA = 6sh + 3√3s².

Question 6: How to determine the Lateral Surface Area of a Hexagonal Prism?

Answer:

Follow the steps mentioned below to determine the lateral surface area of the hexagonal prism:

• Step 1: Note down the values of the apothem length, base length, and height of the given hexagonal prism.
• Step 2: Substitute the given values in the formula of the lateral surface area of a hexagonal prism, LSA = 6sh. 
• Step 3: Write the resulting value in square units.

Призма — это одна из объемных фигур, свойства которой изучают в школе в курсе пространственной геометрии. В данной статье рассмотрим конкретную призму — шестиугольную. Что это за фигура, как найти объем правильной шестиугольной призмы и площадь ее поверхности? Ответы на эти вопросы содержатся в статье.

Фигура призма

Предположим, что мы имеем произвольный многоугольник с числом сторон n, который находится в некоторой плоскости. К каждой вершине этого многоугольника построим вектор, который не будет лежать в плоскости многоугольника. С помощью этой операции мы получим n одинаковых векторов, вершины которых образуют многоугольник, в точности равный исходному. Фигура, ограниченная двумя одинаковыми многоугольниками и параллельными линиями, соединяющими их вершины, называется призмой.

Гранями призмы являются два основания, представленные многоугольниками с n сторонами, и боковые n поверхностей-параллелограммов. Количество ребер Р фигуры связано с числом ее вершин В и граней Г формулой Эйлера:

Р = В + Г — 2

Для многоугольника с n сторонами получаем n + 2 грани и 2 * n вершин. Тогда количество ребер будет равно:

Р = В + Г — 2 = 2 * n + n + 2 — 2 = 3 * n

При изучении стереометрии в старших классах школ рассматривают свойства фигур в пространстве. Одним…

Самой простой призмой является треугольная, то есть основанием у нее является треугольник.

Классификация призм достаточно разнообразна. Так, они могут быть правильными и неправильными, прямоугольными и косоугольными, выпуклыми и вогнутыми.

Шестиугольная призма

Эта статья посвящена вопросу объема правильной шестиугольной призмы. Сначала познакомимся ближе с этой фигурой.

Как следует из названия, основание шестиугольной призмы является многоугольником с шестью сторонами и шестью углами. В общем случае таких многоугольников можно составить великое множество, однако для практики и для решения геометрических задач важен один единственный случай — правильный шестиугольник. У него все стороны равны между собой, а каждый из 6 углов составляет 120 ^o. Построить этот многоугольник можно легко, если разделить окружность на 6 равных частей тремя диаметрами (они должны пересекаться под углами 60 ^o).

Правильная шестиугольная призма предполагает не только наличие правильного многоугольника в ее основании, но и тот факт, что все боковые стороны фигуры должны являться прямоугольниками. Это возможно только в случае, если боковые грани будут перпендикулярны шестиугольным основаниям.

Правильная шестиугольная призма — это достаточно совершенная фигура, которая встречается в быту и природе. Стоит только вспомнить о форме пчелиных сот или о шестигранном гаечном ключе. В области нанотехнологий также часто встречаются шестиугольные призмы. Например, кристаллические решетки ГПУ и C32, которые реализуются при определенных условиях в титане и цирконии, а также решетка графита имеют форму шестиугольных призм.

Площадь поверхности шестиугольной призмы

Перейдем теперь непосредственно к вопросу вычисления площади и объема призмы. Сначала рассчитаем площадь поверхности этой фигуры.

Площадь поверхности любой призмы вычисляется с помощью следующего равенства:

S = 2 * S_o + S_b

То есть искомая площадь S равна сумме площадей двух оснований S_o и площади боковой поверхности S_b. Для определения величины S_o можно поступить двумя способами:

• Вычислить ее самостоятельно. Для этого шестиугольник разбивается на 6 равносторонних треугольников. Зная, что площадь одного треугольника равна половине произведения высоты на основание (длину стороны шестиугольника), можно найти площадь рассматриваемого многоугольника.
• Воспользоваться известной формулой. Она приведена ниже:

S_n = n / 4 * a² * ctg(pi / n)

Здесь a — длина стороны правильного многоугольника, имеющего n вершин.

Очевидно, что оба способа приводят к одному результату. Для правильного шестиугольника площадь равна:

S_o = S₆ = 3 * √3 * a² / 2

Площадь боковой поверхности найти просто, для этого следует умножить основание каждого прямоугольника a на высоту призмы h, полученное значение умножить на число таких прямоугольников, то есть на 6. В итоге:

S_b = 6 * a * h

Пользуясь формулой для полной площади поверхности, для правильной шестиугольной призмы получаем:

S = 3 * √3 * a² + 6 * a * h = 3 * a * (√3 * a + 2 * h)

Как найти объем призмы?

Объем — это физическая величина, которая отражает область пространства, занимаемую объектом. Для призмы рассчитать эту величину можно по следующей формуле:

V = S_o * h

Это выражение дает ответ на вопрос о том, как найти объем призмы произвольной формы, то есть необходимо площадь основания S_o умножить на высоту фигуры h (расстояние между основаниями).

Заметим, что приведенное выражение справедливо для любой призмы, включая вогнутые и косоугольные фигуры, образованные неправильными многоугольниками в основании.

Формула объема призмы шестиугольной правильной

На данный момент мы рассмотрели все необходимые теоретические выкладки, чтобы получить выражение для объема рассматриваемой призмы. Для этого достаточно площадь основания умножить на длину бокового ребра, которая является высотой фигуры. В итоге формула объема шестиугольной призмы примет вид:

V = 3 * √3 * a² * h / 2

Таким образом, расчет объема рассматриваемой призмы предполагает знание всего двух величин: длины стороны ее основания и высоты. Эти две величины однозначно определяют объем фигуры.

Сравнение объемов шестиугольной призмы и цилиндра

Выше было сказано, что основание шестиугольной призмы может быть легко построено с использованием окружности. Также известно, что если увеличивать число сторон правильного многоугольника, то его форма будет приближаться к окружности. В связи с этим представляет интерес рассчитать, на сколько объем правильной шестиугольной призмы отличается от этого значения для цилиндра.

Для ответа на поставленный вопрос необходимо вычислить длину стороны шестиугольника, вписанного в окружность. Можно легко показать, что она равна радиусу. Обозначим радиус окружности буквой R. Предположим, что высота цилиндра и призмы равна некоторому значению h. Тогда объем призмы равен следующему значению:

V_p = 3 * √3 * R² * h / 2

Объем цилиндра определяется по той же формуле, что и объем для произвольной призмы. Учитывая, что площадь круга равна pi * R², для объема цилиндра имеем:

V_с = pi * R² * h

Найдем отношение объемов этих фигур:

V_p / V_с = 3 * √3 * R² * h / 2 / (pi * R² * h) = 3 * √3 / (2 * pi)

Число «пи» равно 3,1416. Подставляя его, получаем:

V_p / V_с = 0,827

Таким образом, объем правильной шестиугольной призмы составляет около 83 % от объема цилиндра, в который она вписана.