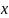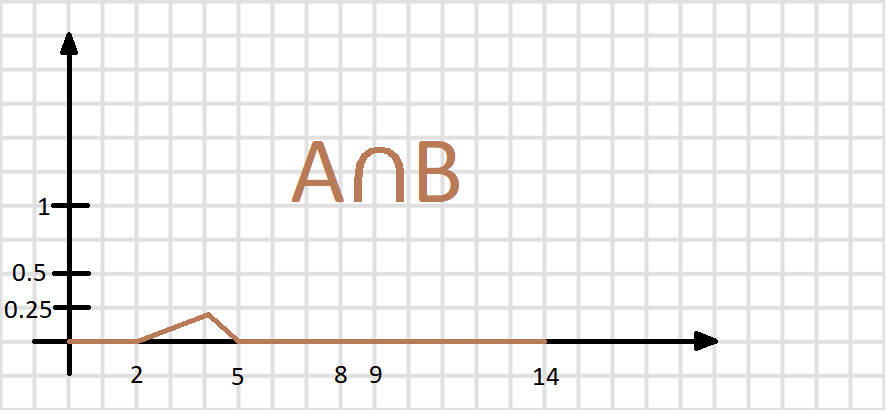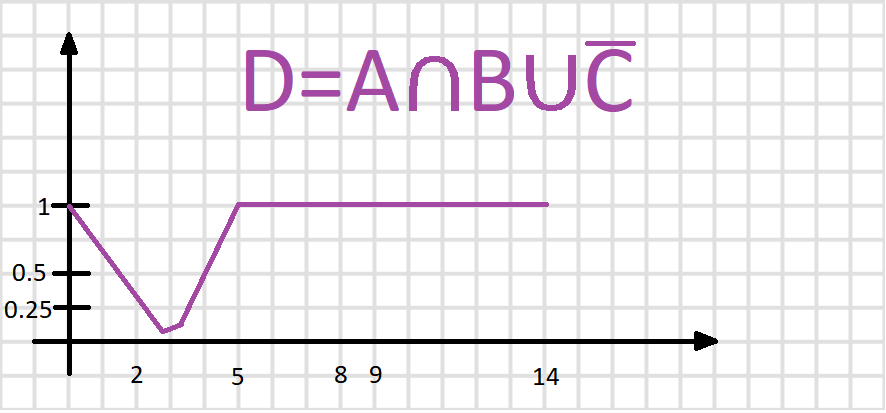Как найти носитель нечеткого множества

Обобщение понятия принадлежности. В рассмотренных примерах характеристическая функция принимала значения 0 или 1. Предположим, что характеристическая функция принимает любое значение из . Тогда элемент может не принадлежать множеству , принадлежать в какой-либо степени или быть элементом множества .

Нечёткое множество. Нечётким подмножеством (нечётким множеством) множества называется множество упорядоченных пар , где – функция принадлежности элемента множеству , характеризующая степень принадлежности элемента этому множеству, или, другими словами, меру соответствия элемента универсального множества свойствам нечёткого множества . В случае непрерывного множества для задания нечёткого множества используют такое обозначение: .

Множество принадлежностей. Множество значений функции принадлежности называется Множеством принадлежностей. Если , то – обычное множество, т. е. чёткое множество можно рассматривать как предельный случай нечёткого множества. Далее в этом учебном пособии множество принадлежностей .

Мощность нечёткого множества. Пусть на универсальном множестве задано нечёткое множество . Мощность нечёткого множества или его Кардинальное число определяется следующим образом: .

Пример 28. На универсальном множестве определим следующее нечёткое множество:

.

Определим кардинальное число нечёткого множества :

Принадлежность элемента нечёткому множеству можно обозначать и так: .

Для определения степени принадлежности элемента нечёткому множеству существует специальная терминология. Так, нечёткое множество , заданное в Примере 28, содержит в незначительной степени элемент , не содержит , в небольшой степени содержит , в значительной степени – и , и содержит элемент .

Пример 29. Нечёткое множество небольших натуральных чисел может быть задано, например, так:

Замечание. Значения заданы субъективно.

Носитель нечёткого множества. Носителем (суппортом) нечёткого множества (supp) называется множество элементов , для которых . Нечёткое множество называется пустым, если его носитель является пустым множеством.

Ядро нечёткого множества. Ядром Нечёткого множества () называется множество элементов , для которых .

Высота нечёткого множества. Величина ( для дискретных универсальных множеств) называется Высотой нечёткого множества ().

Нормальные и субнормальные нечёткие множества. Нечёткое множество Нормально, если его высота равна 1. Если высота меньше 1, то нечёткое множество называется Субнормальным. Всякое непустое субнормальное нечёткое множество можно преобразовать к нормальному , нормируя его функцию принадлежности:

.

Унимодальные нечёткие множества. Нечёткое множество называется Унимодальным, если только для одного .

Точки перехода нечётких множеств. Элементы , для которых , называются Точками перехода нечёткого множества .

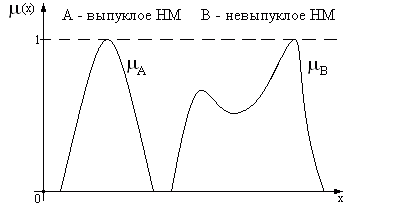
Выпуклые нечёткие множества. Нечёткое множество называется Выпуклым, если:

.

Пример 30. Пусть универсальное множество есть множество действительных чисел, т. е. . Определим нечёткое множество как множество чисел, близких к числу (Рис. 4).

Рисунок 4

Функцию принадлежности можно задать следующим образом: , где . Показатель степени выбирается в зависимости от степени близости к . Например, для описания множества чисел, очень близких к , можно взять ; для множества чисел, не очень далеких от , .

Пример 31. На универсальном множестве из Примера 28 Задано нечёткое множество . Для нечёткого множества : 1) определить его мощность; 2) определить носитель, ядро и высоту; 3) выяснить, является ли оно нормальным или субнормальным. Если является субнормальным, преобразовать его к нормальному; 4) проверить, будет ли полученное множество унимодальным; 5) определить точки перехода .

Решение.

1. По определению, мощность (кардинальное число) нечёткого множества , заданного на конечном универсальном множестве , определяется по формуле: .

Тогда .

2. Воспользуемся определениями носителя, ядра и высоты нечёткого множества. Очевидно, , , .

3. Заданное нечёткое множество является субнормальным. Построим соответствующее ему нечёткое нормальное множество . Для этого вычислим значения функции принадлежностей элементов по формуле:

.

Имеем: , аналогично: , , , , . Таким образом, нечёткое нормализованное множество .

4. Множество является унимодальным, так как содержит только один элемент , для которого .

5. Множество имеет единственную точку перехода – , так как только .

Умножение нечётких множеств на число. Если – такое положительное число, что , то для нечёткого множества функция принадлежности определяется следующим образом: .

Сравнение нечётких множеств. Рассмотрим два нечётких множества и , заданных на универсальном множестве .

Говорят, что Содержится в , т. е. , если для любого . Графически это означает, что кривая, задающая нечёткое множество располагается выше аналогичной кривой нечёткого множества . Если условие включения выполняется не для всех , то говорят о Степени включения в , которая определяется как , где – множество , на котором выполняется условие включения.

Два нечётких множества и Равны, если они содержатся друг в друге, т. е. , если для любого .

Подмножество -уровня. Подмножеством -уровня нечёткого множества , , называется чёткое подмножество элементов , для которых . Множество называют также -сечением нечёткого множества . При этом, если , то говорят о сильном сечении, а если , то о слабом сечении. Имеет место Важное свойство: если , то .

Для задач анализа и синтеза нечётких множеств применяют Теорему о декомпозиции: нечёткое множество можно разложить по его множествам -уровня следующим образом: , где – произведение числа на множество .

Пример 32. На универсальном множестве определим нечёткое множество . Найдём все подмножества нечёткого множества :

По теореме о декомпозиции нечётких множеств заданное нечёткое множество представим следующим образом:

,

Где , т. е.

Определение нечеткого множества

Рассмотрим снова формулу (6.3) определяющую характеристическую функции . Профессор Lotfi Zadeh в 1965 году опубликовал статью, которая называлась «Fuzzy sets», которой он расширил двузначную логику до ограниченной многозначной оценки. Выше 0 и ниже 1, то есть в интервал [0,1] и впервые вел понятие нечеткое множество. Здесь вместо термина характеристическая функция использовал функция принадлежности. Нечеткое множество в универсуме U определяется через функцию принадлежности следующим образом:

Величина  означает субъективную оценку степени принадлежности x множеству A. Заранее не постулируется, какого вида эта оценка. Четкое множество является частным случаем нечеткого множества.

Заметим, что нечеткое множество строго определяется с помощью функции принадлежности, таким образом, логика определения понятия нечеткого множества не содержит какой-либо нечеткости.

Определение 6.1. Нечетким множеством A на универсуме U будем называть совокупность упорядоченных пар  (6.5) , составленных из элементов x универсума U и соответствующей степеней принадлежности .

Пример:

Обычно нечеткое  множество отождествляется с его функцией .

Рекомендуемые материалы

Замечание: Определение нечеткого множества с помощью определения 6.1 является одним из возможных подходов формализации нечеткости. Функция может принимать не значение из интервала, а целый интервал из интервала.

 6.2.3 Основным характеристики нечетких множеств

Определение 6.2. Носителем нечеткого множества А называется обычное подмножество таких точек из универсума U, для которых величина  . Носитель обозначается:  .

  (6.6)

Определение 6.3. Высотой нечеткого множества A называется величина    (6.7)

Определение 6.4.  Нечеткое множество А называется нормальным, если его высота = 1, в противном случае оно называется субнормальным.

Замечание 6.2. Иногда субнормальное нечеткое множество нормализуют на величину H(A).

Определение 6.5.  Нечеткое множество A называется пустым, если .

Определение 6.6. Множеством α — уровня (альфа — срезом, альфа — сечением) нечеткого множества A называется обычное, то есть четкое подмножество универсума U, определяемого формулой:     (6.8)

Множества строго α — уровня определяются формулой:     (6.9)

Носитель нечеткого множества является частным случаем множества строго α — уровня, то есть    (6.10)

Определение 6.7.  Элементы множества U, для которых степень принадлежности   называются точками перехода.

Определение 6.8. Нечеткое множество А в универсуме U ()  называется выпуклым нечетким множеством тогда и только тогда, когда его функция принадлежности выпукла, то есть для каждой пары точек  выполняется условие:    (6.11)

 6.2.4 Операции над нечеткими множествами

Пусть А,В нечеткие множества на универсуме U.

Определение 6.9. Равенство: говорят, что А и В равны и пишут А=В, если    (6.12)

Определение 6.10. Операция включения: говорят А содержится в В, или нечеткое множество А является нечетким подмножеством нечеткого множества В и пишут     (6.13)

Строгое включение или строгое подмножество имеет место, когда хотя бы одно из неравенств (6.13) является строгим.

Когда А является подмножеством В, т.е. , говорят что В доминирует А.

«7 — Опорно-двигательная система клетки» — тут тоже много полезного для Вас.

Определение 6.11. Дополнением нечеткого множества А в U называют нечеткое множество  с функцией принадлежности:    (6.14)

Определение 6.12. Объединение нечетких множеств А и В в U, т.е.  называют наименьшее нечеткое множество, включающее как А, так и В с функцией принадлежности вида:  (6.15)

Определение 6.13. Пересечением нечетких множеств А и В в U, т.е.  называют наибольшее нечеткое множество, содержащееся одновременно в А и в В:   (6.16)

Есть и другие определения различных операции.

В теории нечетких множеств много разделов посвящено теории нечетких чисел.

МИНИСТЕРСТВО
ЦИФРОВОГО РАЗВИТИЯ, СВЯЗИ И МАССОВЫХ
КОММУНИКАЦИЙ РОССИЙСКОЙ ФЕДЕРАЦИИ

Ордена
Трудового Красного Знамени федеральное
государственное бюджетное образовательное
учреждение высшего образования

«Московский
технический университет связи и
информатики»

Кафедра
«Информатика»

Лабораторная
работа №6

«Основы
нечеткой
логики»

Выполнил:
студент гр. БСТ2104

Вариант
№17

Проверил:
проф. Семин В.Г.

Москва,
2022 г.

Задание
1. Нахождение основных характеристик
нечеткого множества. Для
заданного дискретного нечеткого
множества А найти носитель, ядро, высоту,
мощность, множества уровня (для заданных
значений α). Указать, является ли данное
множество нормальным. Если является
субнормальным, преобразовать его к
нормальному. проверить является ли
нормализованное множество унимодальным.

Решение:

Найдем
носитель нечёткого множества:

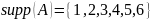
Найдем
ядро нечёткого множества:

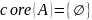
Найдём
высоту нечёткого множетсва:

Найдем
мощность нечёткого множества:

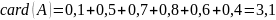
Найдем
множества уровня для значения α
= 0,6:

Найдем
множества уровня для значения α
= 0,9:

Так
как высота нечеткого множества равна
0,8 , то оно является субнормальным.
Преобразуем нечеткое множество к
нормальному:

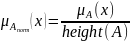
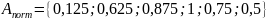
Нормализованное
нечеткое множество является унимодальным,
так как

,
только для одного

.

Задание
2. Операции над нечеткими множествами

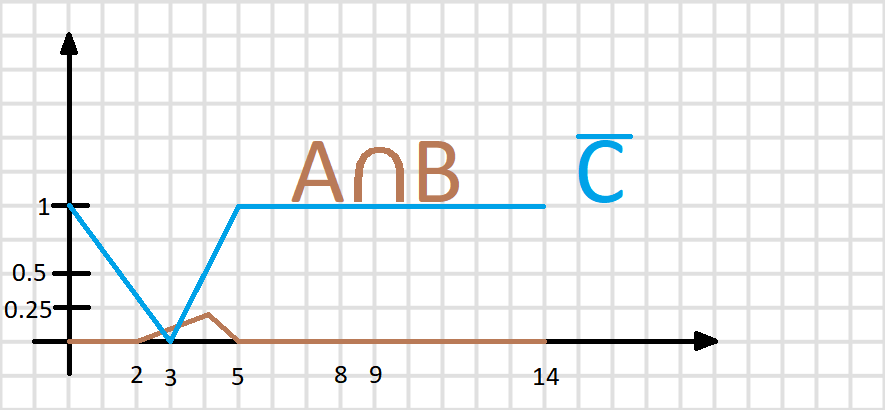
Дано
3 нечетких множества A, B, C (заданы их
функции принадлежности). Построить
функцию принадлежности нечеткого
множества D.

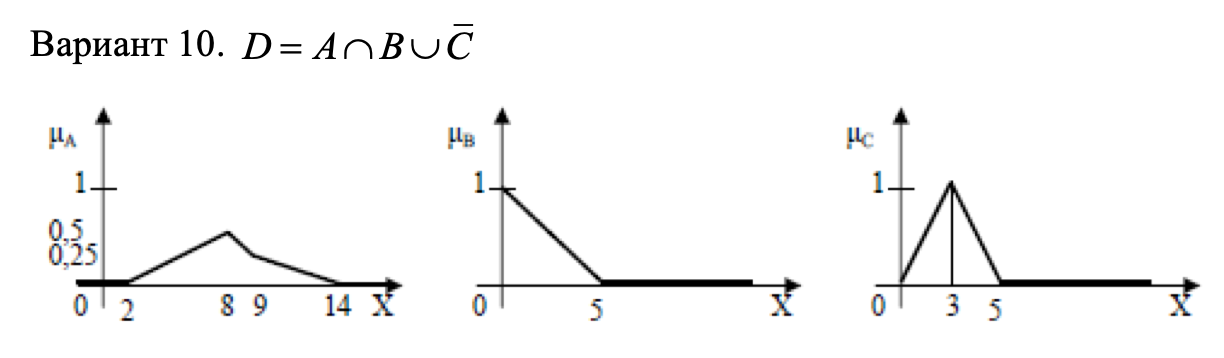
Решение:

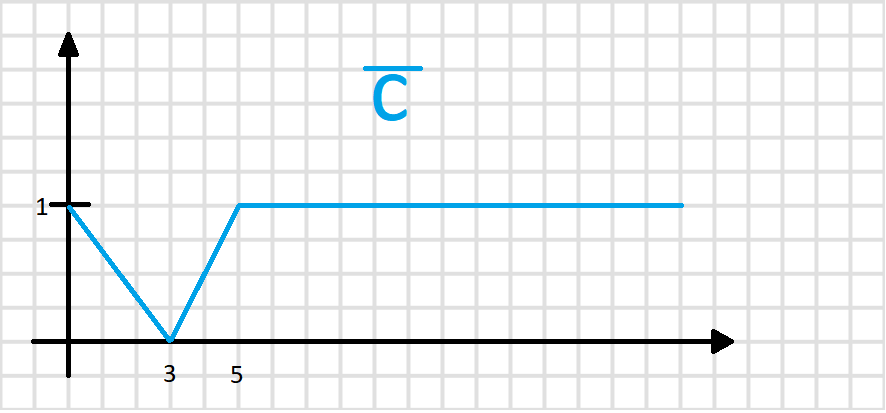
Задание
3. Нечеткие множества А, В и С заданы
таблично. Вычислить значение выражений.

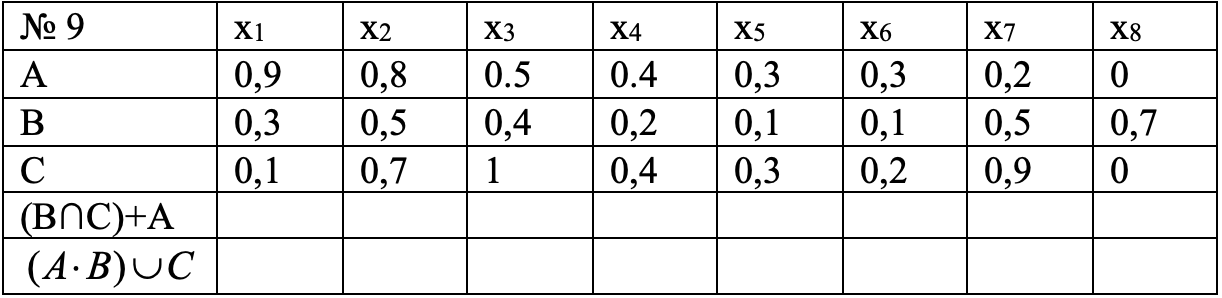
Решение

(B∩C)+A	0,91	0,9	0,7	0,52	0,37	0,37	0,6	0
(A∙B) ∪ С	0,27	0,7	1	0,4	0,3	0,2	0,9	0

А
= 0,9/х1 + 0,8/х2 + 0,5/х3 + 0,4/х4 + 0,3/х5 + 0,3/х6 + 0,2/х7
+ 0/х8

B
= 0,3/х1 + 0,5/х2 + 0,4/х3 + 0,2/х4 + 0,1/х5 + 0,1/х6 + 0,5/х7
+ 0,7/х8

C
= 0,1/х1 + 0,7/х2 + 1/х3 + 0,4/х4 + 0,3/х5 + 0,2/х6 + 0,9/х7 +
0/х8

(B∩C)
= 0,1/х1
+ 0,5/х2 + 0,4/х3 + 0,2/х4 + 0,1/х5 + 0,1/х6 + 0,5/х7 + 0/х8

(B∩C)+A
=
0,91/x1 + 0,9/x2 + 0,7/x3 + 0,52/x4 + 0,37/x5 + 0,37/x6 + 0,6/x7 +
0/x8

(A∙B)
= 0,27/х1 + 0,4/х2 + 0,2/х3 + 0,08/х4 + 0,03/х5 + 0,03/х6 +
0,1/х7 + 0/х8

(A∙B)
∪
С = 0,27/x1
+ 0,7/x2
+ 1/x3
+ 0,4/x4
+ 0,3/x5
+ 0,2/x6
+ 0,9/x7
+ 0/x8

Нечеткое множество(fuzzyset) представляет собой совокупность элементов произвольной природы, относительно которых нельзя точно утверждать –
обладают ли эти элементы некоторым характеристическим свойством, которое используется для задания нечеткого множества.

Пусть

X
– универсальное (базовое) множество,

x
– элемент

X
, а

R
– некоторое свойство. Обычное (четкое) подмножество

A
универсального множества

X
, элементы которого удовлетворяют свойству

R
, определяется как множество упорядоченных пар

A
=

μ
A

x

/
x

, где

μ
A

x

– характеристическая функция, принимающая значение

1
, если

x
удовлетворяет свойству

R
, и

0
– в противном случае.

Нечеткое подмножество отличается от обычного тем, что для элементов

x
из

X
нет однозначного ответа «да-нет» относительно свойства

R
. В связи с этим, нечеткое подмножество

A
универсального множества

X
определяется как множество упорядоченных пар

A
=

μ
A

x

/
x

, где

μ
A

x

– характеристическая функция принадлежности (или просто функция принадлежности), принимающая значения в некотором вполне упорядоченном множестве

M
=

0
;
1

. Функция принадлежности указывает степень (или уровень) принадлежности элемента

x
подмножеству

A
. Множество

M
называют множеством принадлежностей. Если

M
=

0
;
1

, то нечеткое подмножество

A
может рассматриваться как обычное или четкое множество. Степень принадлежности

μ
A

x

является субъективной мерой того, насколько элемент

x
∈
X
, соответствует понятию, смысл которого формализуется нечетким множеством

A
.

Носителем нечеткого множества

A
является четкое подмножество

S
A

универсального множества

X
со свойством

μ
A

x

>
0
, т.е.

S
A

=

x
∣
x
∈
X
∧

μ
A

x

>
0

. Иными словами, носителем нечеткого множества

A
является подмножество

S
A

универсального множества

X
, для элементов которого функция принадлежности

μ
A

x

>
0
больше нуля. Иногда носитель нечеткого множества обозначают

support

A

.

Если носителем нечеткого множества

A
является дискретное подмножество

S
A

, то нечеткое подмножество

A
универсального множества

X
, состоящего из

n
элементов, можно представить в виде объединения конечного числа одноточечных множеств

μ
A

x

/
x
при помощи символа

∑
:

A
=

∑

i
=
1

n

μ
A

x
i

/

x
i

. При этом подразумевается, что элементы

x
i

упорядочены по возрастанию в соответствии со своими индексами, т.е.

x
1

<

x
2

<

x
3

<
…
<

x
n

.

Если носителем нечеткого множества

A
является непрерывное подмножество

S
A

, то нечеткое подмножество

A
универсального множества

X
, рассматривая символ

∫
как непрерывный аналог введенного выше символа объединения для дискретных нечетких множеств

∑
, можно представить в виде объединения бесконечного числа одноточечных множеств

μ
A

x

/
x
:

A
=

∫
X

μ
A

x

/
x
.

Пример. Пусть универсальное множество

X
соответствует множеству возможных значений толщин изделия от

10

мм

до

40

мм

с дискретным шагом

1

мм

. Нечеткое множество

A
, соответствующее нечеткому понятию «малая толщина изделия», может быть представлено в следующем виде:

A
=

1
/
10
;
0,9
/
11
;
0,8
/
12
;
0,7
/
13
;
0,5
/
14
;
0,3
/
15
;
0,1
/
16
;
0
/
17
;
…
;
0
/
40

,

A
=
1
/
10
+
0,9
/
11
+
0,8
/
12
+
0,7
/
13
+
0,5
/
14
+
0,3
/
15
+
0,1
/
16
+
0
/
17
+
…
+
0
/
40
,

где знак суммирования обозначает не операцию арифметического сложения, а объединения элементов в одно множество. Носителем
нечеткого множества

A
будет конечное подмножество (дискретный носитель):

S
A

=

10
;
11
;
12
;
13
;
14
;
15
;
16

.

Если же универсальное множество

X
является множеством действительных чисел от

10
до

40
, т.е. толщина изделия может принимать все возможные значения в этих пределах, то носителем нечеткого множества

A
является отрезок

S
A

=

10
;
16

.

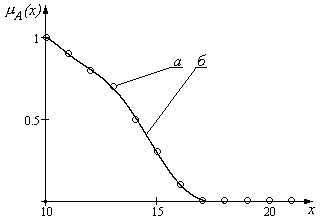
Нечеткое множество с дискретным носителем может быть представлено в виде отдельных точек на плоскости, нечеткое множество
с непрерывным носителем может быть представлено в виде кривой, что соответствует дискретной и непрерывной функциям принадлежности

μ
A

x

, заданным на универсальном множестве

X
(рис.2.1).

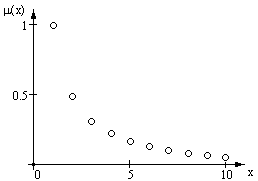
Пример. Пусть

X
=

0
;
1
;
2
;
…

– множество целых неотрицательных чисел. Нечеткое множество

ital
малый

можно определить как

μ

ital
малый

x

=

x

1
+

0,1
x

2

−
1

.

Нечеткое множество

A
называется конечным, если его носитель

S
A

является конечным четким множеством. При этом, по аналогии с обычными множествами, можно говорить, что такое нечеткое множество
имеет конечную мощность

card

A

=

card

S
A

. Нечеткое множество

A
называется бесконечным, если его носитель

S
A

не является конечным четким множеством. При этом счетным нечетким множеством будет называться нечеткое множество с счетным носителем, имеющим счетную мощность в обычном смысле в терминах теории четких множеств, т.е. если

S
A

содержит бесконечное число элементов, которые однако можно пронумеровать натуральными числами

1,2
,3
.
.
.
, причем достичь последнего элемента при нумерации принципиально невозможно. Несчетным нечетким множеством будет называться нечеткое множество со несчетным носителем, имеющим несчетную мощность континуума, т.е. если

S
A

содержит бесконечное число элементов, которые невозможно пронумеровать натуральными числами

1,2
,3
.
.
.

Пример. Нечеткое понятие «очень маленькое количество деталей» может быть представлено в виде конечного нечеткого множества

A
=
1
/
0
+
0,9
/
1
+
0,8
/
2
+
0,7
/
3
+
0,5
/
4
+
0,1
/
5
+
0
/
6
+
…
с мощностью

card

(
A
)
=
6
и носителем

S
A

=

0
;
1
;
2
;
3
;
4
;
5

, который является конечным четким множеством. Нечеткое понятие «очень большое количество деталей» может быть представлено
в виде

A
=
0
/
0
+
…
+
0,1
/
1
0
+
0,4
/
11
+
0,7
/
12
+
0,9
/
13
+
1
/
14
+
1
/
15
+
…
+
1
/
n
+
…
,
n
∈
N
– нечеткого множества с бесконечным счетным носителем

S
A

≡
N
(множество натуральных чисел), который имеет счетную мощность в обычном смысле.

Пример. Несчетное нечеткое множество

A
, соответствующее нечеткому понятию «очень горячо», задано на универсальном множестве значений температур (в Кельвинах) температурой

x
∈
[
0
;
∞
)
и функцией принадлежности

μ
A

=
1
−

e

−
x

, с носителем

S
A

≡

R

+

(множество неотрицательных действительных чисел), который имеет несчетную мощность континуума.

Величина

sup

x
∈
X

μ
A

x

называется высотой нечеткого множества.

Нечеткое множество

A
нормально, если его высота равна

1
, т.е. верхняя граница его функции принадлежности

sup

x
∈
X

μ
A

x

=
1
. При

sup

x
∈
X

μ
A

x

<
1
нечеткое множество называется субнормальным.

Нечеткое множество называется пустым, если

∀
x
∈
X

μ
A

x

=
0
.

Непустое субнормальное множество всегда можно нормализовать, разделив все значения функции принадлежности на ее максимальное
значение

μ
A

x

sup

x
∈
X

μ
A

x

.

Нечеткое множество называется унимодальным, если

μ
A

x

=
1
только для одной точки

x
(моды) универсального множества

X
.

Нечеткое множество называется точечным, если

μ
A

x

>
0
только для одной точки

x
универсального множества

X
.

Множеством
α
-уровня нечеткого множества

A
, определенного на универсальном множества

X
, называется четкое подмножество

A
α

универсального множества

X
, определяемое в виде:

A
α

=

x
∈
X
∣

μ
A

x

≥
α

, где

α
∈

0
;
1

.

Пример.
A
=
0,8
/
1
+
0,6
/
2
+
0,2
/
3
+
1
/
4
,

A
0,5

=

1
;
2
;
4

, где

A
0,5

– четкое множество, включающее те элементы

x
упорядоченных пар

μ
A

x

/
x
, составляющих нечеткое множество

A
, для которых значение функции принадлежности которых удовлетворяет условию

μ
A

x

≥
α
.

Для множеств

α
-уровня выполняется следующее свойство: если

α
1

≥

α
2

, то мощность подмножества

A

α
1

не больше мощности подмножества

A

α
2

.

Элементы

x
∈
X
, для которых

μ
A

x

=
0,5
называются точками перехода нечеткого множества

A
.

Ядром нечеткого множества

A
, определенного на универсальном множестве

X
, называется четкое множество

core

A

, элементы которого удовлетворяют условию

core

A

=

x
∈
X
∣

μ
A

x

=
1

.

Границей нечеткого множества

A
, определенного на универсальном множестве

X
, называется четкое множество

front

A

, элементы которого удовлетворяют условию

front

A

=

x
∈
X
∣
0
<

μ
A

x

<
1

.

Пример.Пусть

X
=

0
;
1
;
2
;
…
;
10

,

M
=

0
;
1

. Нечеткое множество

несколько

можно определить на универсальном множестве натуральных чисел следующим образом:

несколько

=
0,5
/
3
+
0,8
/
4
+
1
/
5
+
1
/
6
+
0,8
/
7
+
0,5
/
8
; его характеристики:

высота

=
1
,

носитель

=

3
;
4
;
5
;
6
;
7
;
8

,

точки

перехода

=

3
;
8

,

ядро

=

5
;
6

,

граница

=

3
;
4
;
7
;
8

.

Нечеткое множество

A
, определенное на универсальном множестве

X
, называется выпуклым, если

μ
A

x

≥
min

μ
A

a

;

μ
A

b

;
a
<
x
<
b
;
x
,
a
,
b
∈
X
(рис.2.3).