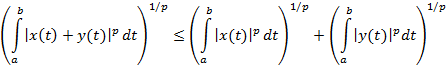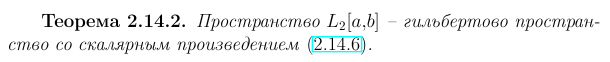Как найти норму функционала

Мы решали подобные задания в прошлом семестре, если ещё «моск не вынесли» мне функаном и нигде не напутал

Сначала вроде надо заметить, что для функционала вида

[math]f(x)=intlimits_{a}^{b}mu(t)x(t),dt[/math]

с неотрицательной на [math][a,b][/math] функцией [math]mu(t)[/math] норма вычисляется по формуле

[math]|f|=intlimits_{a}^{b}mu(t),dt[/math]

Для заданного функционала функция [math]mu(t)=t^2-2t-3[/math] знакопеременна на отрезке [math][0,7/2][/math], поэтому вроде можно воспользоваться следующим приёмом: установив оценку [math]|f(x)|leqslantalpha|x|[/math], построим последовательность элементов [math]{x_n}subsetsigma(theta,1)[/math] таких, что [math]|f(x_n)|toalpha[/math] при [math]ntoinfty[/math]. Последнее будет означать, что [math]|f|=alpha[/math].

Оценим величину [math]|f(x)|[/math]:

[math]|f(x)|leqslantintlimits_{0}^{7/2}|t^2-2t-3||x(t)|,dtleqslantBiggl[intlimits_{0}^{3}(3+2t-t^2),dt+intlimits_{3}^{7/2}(t^2-2t-3),dtBiggl]|x|_C=frac{229}{24}|x|_C[/math]

так что функционал [math]f[/math] и [math]|f|leqslantfrac{229}{24}[/math]. Покажем, что [math]|f|=frac{229}{24}[/math]. Для этого построим «срезывающую» последовательность непрерывных функций [math]x_n(t)in C[0,7/2][/math] следующего вида

[math]x_n(t)=begin{cases}-1,&text{if}quad tinleft[0,,3-dfrac{1}{n}right]\[8pt]nt-3n,&text{if}quad |t-3|leqslantdfrac{1}{n}\[8pt]1,&text{if}quad tinleft[3+dfrac{1}{n},,dfrac{7}{2}right]end{cases}[/math]

Теперь осталось вычислить предел последовательности [math]{|f(x_n)|}[/math]

[math]begin{aligned}lim_{ntoinfty}|f(x_n)|&=lim_{ntoinfty},Biggl|intlimits_{0}^{3-tfrac{1}{n}}(3+2t-t^2),dt+nintlimits_{|t-3|leqslanttfrac{1}{n}}(t^2-2t-3)(t-3),dt+intlimits_{3+tfrac{1}{n}}^{7/2}(t^2-2t-3),dtBiggl|,=\[3pt]&=lim_{ntoinfty},Biggl|frac{229}{24}-frac{4}{n^2}+nintlimits_{|t-3|leqslanttfrac{1}{n}}(t^3-5t^2+3t+9),dtBiggl|,=\[3pt]&=lim_{ntoinfty}left|frac{229}{24}-frac{4}{3n^2}right|=frac{229}{24}end{aligned}[/math]

откуда следует, что [math]|f|=frac{229}{24}[/math].

Норма(обозначается
||x||)
– такое число, поставленное в соответствие
вектору х, для которого выполняются
следующие свойства:

1. ||x||≥0,
   ||x||=0
   только в том случае, если х=0

2. ||аx||=|a|*||x||

3. ||x+у||≤||x||+||у||

Пример:

Пространство R^m
, на котором можно ввести несколько
различных норм

1. Определение пространств c[0,1], cl[a,b], l1[a,b] со стандартной нормой.

С[a,
b]
– пространство непрерывных на [a,
b]
функций, где определена норма:

Следовательно
в частности пространство C[0,1]
– функции непрерывные на [0,1] с нормой

вероятно
CL[a,b]
это С^(к)
[a,b] – пространство непрерывно
дифференцируемых к раз функций с нормой:

Если
в этом же пространстве ввести другую
норму:

То
получится пространство L_p[a,b]
, его частный случай L₁[a,b]
имеет стандартную норму:

1. Определение и примеры эквивалентных
   норм в нормированном векторном
   пространстве.

Пример:

в

1. Определение и примеры банаховых
   пространств.

1. Сформулировать теорему «Принцип
   вложенных шаров».

Пусть в Банаховом пространстве X
дана последовательность замкнутых
шаров

вложенных друг в друга

причем

. Тогда в Х существует единственная
точка, принадлежащая всем шарам.

1. Сформулировать теорему «Принцип
   сжимающих отображений».

Пусть отображение f
отображает замкнутое в банаховом
пространстве E множество
M в себя и является на M
сжимающим с коэффициентом
сжатия α.
Тогда на множестве M
отображение f имеет
единственную неподвижную точку x*,
которая может быть найдена методом
последовательных приближений:

,
n=1,2…

где (x)M
и x_nx*
при n.
Кроме того, справедлива оценка скорости
сходимости

1. Записать неравенства Гельдера и
   Минковского.

Пусть

и

– число, сопряжённое к нему ().
Тогда для любых функций
и
,
заданных на
,
для которых существуют интегралы

и

имеет место неравенство Гельдера

Пусть

и пусть функции x(t)
и y(t)
таковы, что существуют и конечны интегралы
,
тогда справедливо неравенство
Минковского

1. Определение пространства
   L_p[a,b].

Пространством
называется
нормированное векторное пространство,
элементами которого являются классы
эквивалентных между собой интегрируемых
по Лебегу функций со степенью p
и нормой

Сходимость в пространстве

называется сходимостью в среднем со
степенью p.

1. Определение и примеры открытых
   и замкнутых множеств в нормированных
   векторных пространствах.

1. Определение и примеры компактных
   и предкомпактных множеств в нормированных
   векторных пространствах.

1. Определение и примеры предгильбертовых
   и гильбертовых пространств. Определение
   пространств l₂
   и L₂[a,b].

1. Определение нормы, согласованной со
   скалярным произведением, в гильбертовом
   пространстве.

1. Сформулировать теорему о проекции в
   гильбертовом пространстве.

Теорема(о проекции в Н)

Пусть Н — гильбертово пространство, L
H – его замкнутое векторное
подпространство.
Для любого элемента

существует единственная его проекция
на подпространство L, т.
е.

.

1. Определение и примеры полных
   ортонормированных систем в пространстве
   L₂[-1,1].

Множество {x_a}
ненулевых векторов евклидова (гильбертова)
пространства со скалярным
произведением  такое,
что (x_a,
x_ab)=0
при .
Если при этом норма каждого вектора
равна единице, то система {x_a}
наз. ортонормированной. Полная О. с. {x_a}
наз. ортогональным (ортонормированным)
базисом.

1. Определение и примеры
   ограниченных линейных операторов в
   НВП.

1. Определение и примеры
   вычисления нормы линейных ограниченных
   операторов.

1. Определение и примеры ограниченных
   линейных функционалов.

Пример:

1. Сформулировать теорему Рисса об общем
   виде ограниченного линейного функционала
   на гильбертовом пространстве.

Для любого
линейного ограниченного функционала  на
гильбертовом пространстве  существует
единственный вектор  такой,
что  для
любого .
При этом норма линейного функционала совпадает
с нормой вектора :

.
Теорема также означает, что пространство
всех линейных ограниченных функционалов
над изоморфно пространству .

1. Сформулировать классическую теорему
   Хана-Банаха в случае нормированного
   векторного пространства над полем R.
   

1. Определение и примеры
   компактных линейных операторов в НВП.

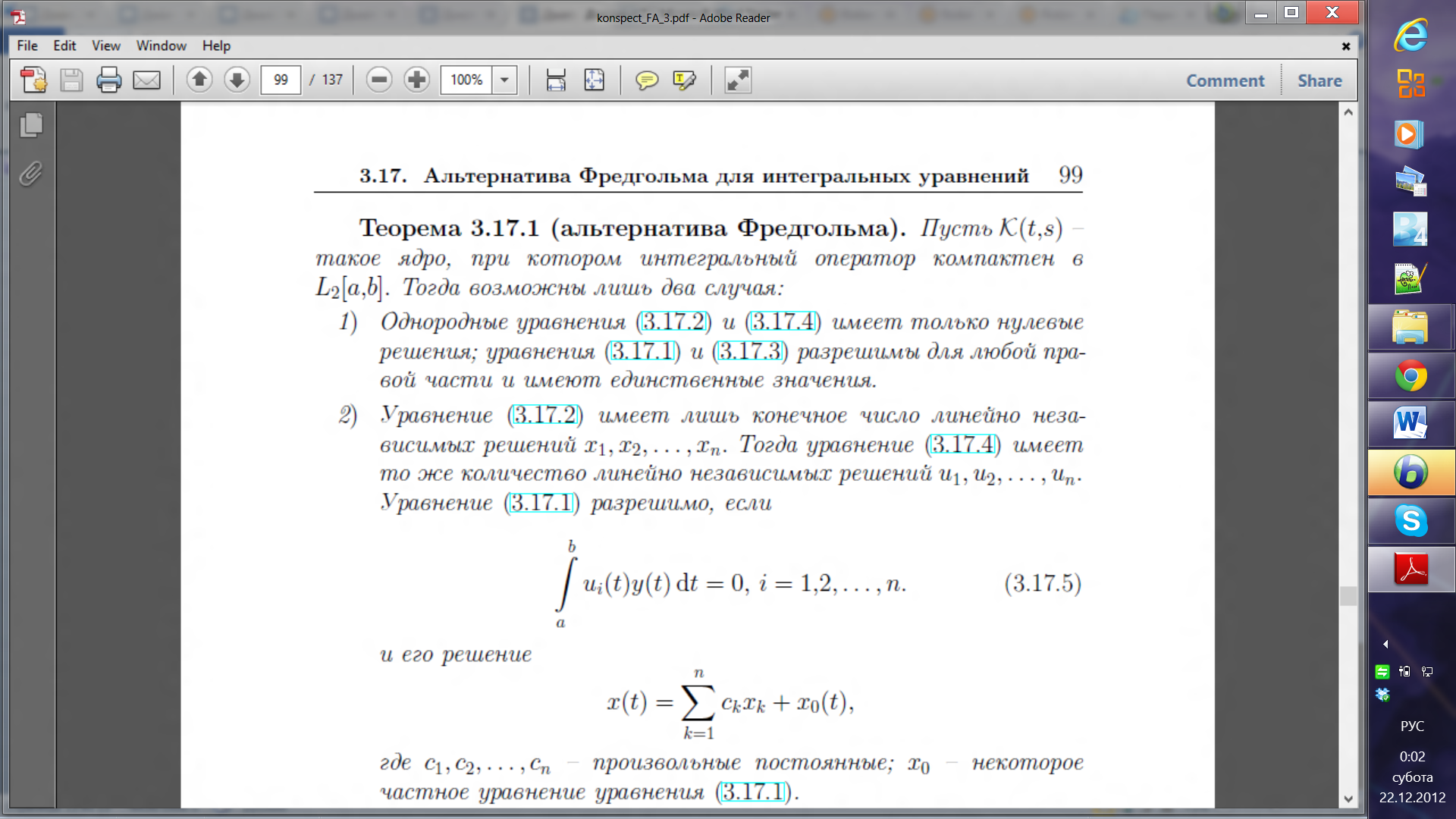
1. Сформулировать основную теорему
   Фредгольма для уравнений с интегральными
   операторами в пространстве L₂[a,b].

Соседние файлы в папке ФАН

• #
• #
• #
• #

1. Является ли функционал, линейным непрерывным и если да, то найти его норму.

Решение:

Замечание: Интеграл, стоящий в определении функционала, может быть несобственным, т. к. точка входит в отрезок . Для корректности поставленной задачи, будем считать, что функционал Действует из подпространства , где .

. Получили линейность.

Оценим норму, одновременно докажем ограниченность функционала (следовательно, его непрерывность):

, здесь применили интегральную форму неравенства Коши-Буняковского. Вычисляя интеграл и применяя выражение для нормы пространства :, получим , этим мы получили оценку для модуля функционала и доказательство ограниченности нашего функционала. Из формулы для выражения нормы функционала:Получим .

Теперь, положим

Вычислим А так как

Получим

2. Является ли функционал линейным непрерывным и если да, то найти его норму.

Решение: Будем считать что функционал действует из .

Функционал не является линейным. Пример:

Тем самым доказано, что Получили ограниченность функционала. Положим , тогда отсюда

3. Доказать, что оператор является линейным ограниченным оператором и оценить его норму.

Решение:

Доказали линейность.

4. Найти обратный оператор к оператору . Оценить норму .

Решение: Положим получим задачу Коши:

Решая однородное уравнение , найдем .

Согласно методу Лагранжа, решение задачи Коши ищем в виде:

. Где неизвестные функции найдем из системы:

, подставляя , получим систему:

, решая, получим

Где Неизвестные постоянные. Подставляя найденные :

,т. к. .

Для определения получим систему:

.

Решение задачи Коши:

Так как

Оценим норму обратного оператора:

5. Найти сопряженный оператор к оператору

Решение:

Из общего вида линейного функционала в :

.

Так как общий вид линейного функционала представляет собой скалярное произведение в .

Итак:

Это значит, что , т. е. оператор самосопряженный.

6. Является ли оператор вполне непрерывным?

Решение:

Возьмем ограниченное множество . Оператор переводит множество В множество . Если это множество было бы равностепенно непрерывным множеством, то , такое чтоУдовлетворяющих условию

для . (1)

Но это невозможно, т. к. если взять а — подобрать так, чтобы выполнялось условие , то , и выбирая , число можно сделать большим, например, чем 0,5. Это противоречит с (1).

Следовательно, множество не является равностепенно непрерывным и, по теореме Арцела, не является относительно компактным множеством. Значит не может быть вполне непрерывным оператором.