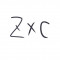Как найти нормаль к плоскости по 3 точкам?
Простой 1 комментарий
В вашем случае, если у вас есть 3 точки, принадлежащие плоскости
ну а дальше просто подставляете эти значения в формулу выше)))
ЗЫ: остается лишь определится с направлением нормали, которое зависит от соглашения по выбору и предоставлению точек A,B,C, которое к слову вы тут не озвучили.
Нормальный вектор плоскости, координаты нормального вектора плоскости
Существует ряд заданий, которым для решения необходимо нормальный вектор на плоскости, чем саму плоскость. Поэтому в этой статье получим ответ на вопрос определения нормального вектора с примерами и наглядными рисунками. Определим векторы трехмерного пространства и плоскости по уравнениям.
Нормальный вектор плоскости – определение, примеры, иллюстрации
Чтобы материал легко усваивался, необходимо предварительно изучить теорию о прямой в пространстве и представление ее на плоскости и векторы.
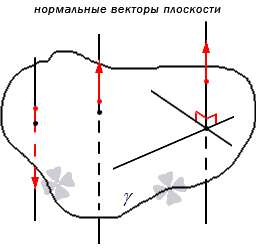
Нормальным вектором плоскости считается любой ненулевой вектор, который лежит на перпендикулярной к данной плоскости прямой.
Отсюда следует, что имеет место существование большого количества нормальных векторов в данной плоскости. Рассмотрим на рисунке, приведенном ниже.
Нормальные векторы располагаются на параллельных прямых, поэтому они все коллинеарны. То есть, при нормальном векторе n → , расположенном в плоскости γ , вектор t · n → , имея ненулевое значение параметра t , также нормальный вектор плоскости γ . Любой вектор может быть рассмотрен как направляющий вектор прямой, которая перпендикулярна этой плоскости.
Имеются случаи совпадения нормальных векторов плоскостей из-за перпендикулярности одной из параллельных плоскостей, так как прямая перпендикулярна и второй плоскости. Отсюда следует, что нормальные векторы перпендикулярных плоскостей должны быть перпендикулярными.
Рассмотрим на примере нормального вектора на плоскости.
Задана прямоугольная система координат О х у z в трехмерном пространстве. Координатные векторы i → , j → , k → считаются нормальными векторами плоскостей O y z , O x z и O x y . Это суждение верно, так как i → , j → , k → ненулевые и расположены на координатных прямых O x , O y и O z . Эти прямые перпендикулярны координатным плоскостям O y z , O x z и O x y .
Координаты нормального вектора плоскости – нахождение координат нормального вектора плоскости из уравнения плоскости
Статья предназначена для того, чтобы научить находить координаты нормального вектора плоскости при известном уравнении плоскости прямоугольной системы координат О х у z . Для определения нормального вектора n → = ( A , B , C ) в плоскости необходимо наличие общего уравнения плоскости, имеющее вид A x + B y + C z + D = 0 . То есть достаточно иметь уравнение плоскости, тогда появится возможность для нахождения координат нормального вектора.
Найти координаты нормального вектора, принадлежащего плоскости 2 x — 3 y + 7 z — 11 = 0 .
По условию имеем уравнение плоскости. Необходимо обратить внимание на коэффициенты, так как они и являются координатами нормального вектора заданной плоскости. Отсюда получаем, что n → = ( 2 , — 3 , 7 ) — это нормальный вектор плоскости. Все векторы плоскости задаются при помощи формулы t · n → = 2 · t , — 3 · t , 7 · t , t является любым действительным числом не равным нулю.
Ответ: n → = ( 2 , — 3 , 7 ) .
Определить координаты направляющих векторов заданной плоскости x + 2 z — 7 = 0 .
По условию имеем, что дано неполное уравнение плоскости. Чтобы увидеть координаты, необходимо преобразовать уравнение x + 2 z — 7 = 0 к виду 1 · x + 0 · y + 2 z — 7 = 0 . Отсюда получим, что координаты нормального вектора данной плоскости равны ( 1 , 0 , 2 ) . Тогда множество векторов будет иметь такую форму записи ( t , 0 , 2 · t ) , t ∈ R , t ≠ 0 .
Ответ: ( t , 0 , 2 · t ) , t ∈ R , t ≠ 0 .
При помощи уравнения плоскости в отрезках, имеющего вид x a + y b + z c = 1 , и общего уравнения плоскости возможна запись нормального вектора этой плоскости, где координаты равны 1 a , 1 b , 1 c .
Знания о нормальном векторе позволяют с легкостью решать задачи. Часто встречающимися задачами являются задания с доказательствами параллельности или перпендикулярности плоскостей. Заметно упрощается решение задач на составление уравнений заданной плоскости. Если имеется вопрос о нахождении угла между плоскостями или между прямой и плоскостью, то формулы нормального вектора и нахождения его координат помогут в этом.
Нормальный вектор трех точек
Эй, математические выродки, у меня есть проблема, которая ставила меня в тупик некоторое время. Это для личного проекта.
У меня три точки: красная, зеленая и синяя. Они расположены на картонной карточке так, что красная точка находится в левом нижнем углу (0,0), синяя точка-в правом нижнем углу (1,0), а зеленая точка-в левом верхнем углу. Представьте, что вы отступаете назад и фотографируете карту под углом. Если вы должны были найти центр каждой точки На картинке (скажем, единицы пиксели), как бы вы нашли нормальный вектор лица карты на картинке (относительно камеры)?
теперь несколько вещей, которые я подобрал об этой проблеме:
- точки (в реальной жизни) всегда под прямым углом. На картинке они только под прямым углом, если камера была повернута вокруг красной точки вдоль » оси » (ось-линия, созданная красными и синими или красными и зелеными точками).
- есть точки только на одной стороне карта. Таким образом, вы знаете, вы никогда не будете смотреть на это.
- расстояние карты до камеры не имеет значения. Если бы я знал глубину каждой точки, это было бы намного проще (просто простое перекрестное произведение, нет?).
- вращение карты не имеет никакого отношения к тому, что я ищу. В том, что я делал, чтобы попытаться понять это, вращение можно найти с помощью нормального вектора в конце. Будет ли вращение часть (или произведение) нахождения нормального вектора мне неизвестна.
надеюсь, что есть кто-то, кто либо сделал это, либо является математическим гением. Двое моих друзей помогают мне в этом, и до сих пор нам это не удавалось.
6 ответов
Я разработал его в своей старой версии MathCAD:
Edit: неверная формулировка на скриншоте MathCAD: «Known:g и b are перпендикулярно друг с другом»
в MathCAD я забыл последний шаг выполнения кросс-продукта, который я скопирую здесь из моего предыдущего ответа:
теперь мы решили для X-Y-Z переведенные точки g и b, ваши оригинальный вопрос хотел нормальный самолет.
Если крест g x b, мы получим вектор нормальный для обоих:
все значения известны, подключите их (я не буду писать версию с g3 и В3 заменить, так как это просто слишком длинный и уродливый, чтобы быть полезным.
но на практике, я думаю, вам придется решить его численно, регулируя gz и bz чтобы наилучшим образом соответствовать условиям:
g · b = 0
поскольку пиксели не являются алгебраически совершенными.
пример
используя изображение астронавтов Apollo 13, оснащающих один из квадратов командного модуля Канистра с гидроксидом лития для работы в Лэм, я расположил углы:
используя их в качестве основы для плоскости X-Y:
Я записал местоположения пикселей с помощью Photoshop, с положительным X справа и положительным Y вниз (чтобы сохранить правое правило Z»на» картинка):
пробивание двух начальных формул в Excel и использование пакета инструментов анализа для»свернуть » ошибка при регулировке gz и bz, он придумал два значения Z:
b = (-110.8, -62.8, 56.2)
что позволяет мне вычислить другие интересные значения.
длина g и b в пикселях:
g x b = (3710, -15827, -10366)
единица нормальные (длина 1):
масштабирование нормально до той же длины (в пикселях), что и g и b (138.9):
теперь, когда у меня есть нормальный, который имеет ту же длину, что и g и b, я нарисовал их на той же картинке:
Я думаю, у вас будет новая проблема: искажение, введенное объективом камеры. Три точки не идеально проецируются на 2-мерную фотографическую плоскость. Существует сферическое искажение, которое делает прямые линии более не прямыми, делает равные длины более не равными и делает нормали немного отклоненными от нормы.
Microsoft research имеет алгоритм, чтобы выяснить, как исправить для камеры искажение:
но это выше моего понимания:
мы предлагаем гибкий новый метод к легко откалибруйте камеру. Это хорошо подходит для использования без специализированных знание 3D геометрии или компьютер видение. Техника только требует камера для наблюдения за плоским рисунком показано на нескольких (не менее двух) разные ориентации. Либо камера или плоскостная картина могут быть свободно перемещаться. Движение не должно быть известный. Радиальное искажение объектива моделированный. Предлагаемая процедура состоит из решения закрытой формы, с последующим нелинейным уточнением на основе максимального правдоподобия критерий. Оба компьютерного моделирования и реальные данные были использованы для проверки предлагаемая техника и очень хорошая получены результаты. Сравнимый с классическими методами, которые используют дорогие оборудования как 2 или три ортогональные плоскости, предлагаемые техника проста в использовании и гибкий. Он продвигает 3D компьютерных видения один шаг от лабораторных условий к реальное использование.
у них есть образец изображения, где можно увидеть искажение:
Примечание
- вы не знаете, видите ли вы «верхнюю» часть картона или «нижнюю», поэтому Нормаль может быть отражена вертикально (т. е. z = — z)
обновление
Гай нашел ошибку в производных алгебраических формулах. Исправление этого приводит к формулам, которые я, не думаю, имеют простую закрытую форму. Это не так уж плохо, так как его все равно нельзя решить точно; но численно.
вот скриншот из Excel, где я начинаю с двух правил knowns:
g · b = 0
запись 2-го в качестве разницы (сумма» ошибка»), вы можете добавить оба и использовать это значение в качестве числа, чтобы иметь решатель excel свернуть:
Это означает, что вам придется написать свой собственный числовой итерационный решатель. я смотрю на свой численные методы для инженеров учебник из университета; я знаю, что он содержит алгоритмы для решения рекурсивных уравнения без простой замкнутой формы.
из его звуков, у вас есть три точки p1, p2 и p3 определение плоскости, и вы хотите, чтобы найти нормальный вектор к плоскости.
представление точек в виде векторов от начала координат, an уравнение нормального вектора будет
n = (p2 — p1) x (p3 — p1)
(где x-перекрестное произведение двух векторов)
Если вы хотите, чтобы вектор указывал наружу от перед карты, затем Ала правое правило, установить
p1 = красная точка
p2 = синяя (внизу справа) точка
p3 = зеленый (вверху слева) точка
@ Ian Boyd. Мне понравилось ваше объяснение, только я застрял на Шаге 2, Когда вы сказали, чтобы решить для bz. У тебя все еще было bz в вашем ответе, и я не думаю, что вы должны есть!—1—>bz в вашем ответе.
bz должно быть +/- квадратный корень gx 2 + gy 2 + gz 2 — bx 2 — by 2
после того, как я сделал это сам, мне было очень трудно заменить bz в первое уравнение, когда вы решили для гz, потому что при замене bz, сейчас вы получите:
часть, которая затрудняет это, заключается в том, что есть gz в квадратном корне, поэтому вы должны отделить его и объединить gz вместе, и решить для gz что я и сделал, только я не думаю, что мой способ решения был правильным, потому что, когда я написал свою программу для расчета gz для меня, я использовал свой gx и gy значения, чтобы увидеть, соответствует ли мой ответ вашему, и это не так.
так что я подумал, не могли бы вы мне помочь, потому что мне действительно нужно, чтобы это сработало для одного из моих проектов. Спасибо!
просто думаю на ногах здесь.
ваши эффективные входы-это кажущееся соотношение RB / RG [+], кажущийся угол BRG и угол, который (скажем) RB делает с вашей координатной осью Y экрана (я что-то пропустил). Вам нужны компоненты нормализованного нормального (heh!) вектор, который я считаю только двумя независимыми значениями (хотя у вас остается двусмысленность спереди-сзади, если карта просматривается).[++]
поэтому я предполагаю, что это вероятный.
отсюда я работаю над предположением, что кажущийся угол RB всегда равен 0, и мы можем повернуть окончательное решение вокруг оси z позже.
начните с карты, расположенной параллельно плоскости просмотра и ориентированной «естественным» способом (т. е. вы верхний против Нижнего и левого против правого назначений уважаются). Мы можем достичь всех интересных позиций карты, вращаясь на theta вокруг начальной оси x (для -pi/2 ), а затем поворачивать на phi вокруг начальной оси y (для -pi/2 ). Заметим, что мы сохранили видимое направление вектора RB.
следующий шаг вычислить кажущееся отношение и кажущийся угол после в терминах theta и phi и инвертирует результат.[+++]
нормальным будет R_y(phi)R_x(theta)(0, 0, 1) на R_i примитивная матрица вращения вокруг оси i .
[+] абсолютные длины не учитываются, потому что это просто говорит вам расстояние до карты.
[++] Еще одно предположение: расстояние от карты до плоскости просмотра намного больше, чем размер карты.
[++ + ] здесь важна проекция, которую вы используете от трехмерного пространства до плоскости просмотра. Это трудная часть, но не то, что мы можем сделать для вас, если вы не скажете, какую проекцию вы используете. Если вы используете реальную камеру, то это перспективная проекция и освещается практически в любой книге по 3D-графике.
правильный, нормальный вектор не изменяется по расстоянию, но проекция картона на картинке тут изменение по расстоянию (просто: если у вас есть небольшой картон, ничего не меняется. Если у вас есть картон шириной в 1 милю и высотой в 1 милю, и вы поворачиваете его так, чтобы одна сторона была ближе, а другая-дальше, ближняя сторона увеличивается, а дальняя сторона сокращается на картинке. Вы можете сразу увидеть, что прямоугольник не остается прямоугольником, а трапеция)
наиболее точный способ для малых углов и камеры, центрированной на середине, — измерить соотношение ширины / высоты между «нормальным» изображением и угловым изображением на средних линиях (потому что они не деформированы).
мы определяем x как слева направо, y как вниз до вверх, z как далеко до Ближнего.
затем
x = arcsin (measuredWidth/normWidth) красно-синий
y = arcsin (measuredHeight/normHeight) красно-зеленый
Зет= sqrt (1.0-x^2-y^2)
я рассчитаю завтра более точное решение, но сейчас я слишком устал.
вы можете использовать u,v, n co-oridnates. Установите точку обзора в положение «глаза» или «камеры», затем переведите координаты x,y,z в u,v,n. Оттуда вы можете определить нормали,а также перспективные и видимые поверхности,если хотите (u’, v’, n’). Кроме того, имейте в виду, что 2D = 3D с z=0. Наконец, убедитесь, что вы используете однородные координаты.
http://zaochnik.com/spravochnik/matematika/prjamaja-ploskost/normalnyj-vektor-ploskosti-koordinaty-normalnogo-v/
http://askdev.ru/q/normalnyy-vektor-treh-tochek-370805/
Как найти нормальный вектор к плоскости
Нормальным вектором плоскости (или нормалью плоскости) называют вектор, перпендикулярный данной плоскости. Одним из способов задать плоскость является указание координат ее нормали и точки, лежащей на плоскости. Если плоскость задана уравнением Ax+By+Cz+D=0, то нормальным к ней является вектор с координатами (A;B;C). В других случаях для вычисления нормального вектора придется потрудиться.

Инструкция
Пусть плоскость задана тремя принадлежащими ей точками K(xk;yk;zk), M(xm;ym;zm), P(xp;yp;zp). Чтобы найти нормальный вектор, составим уравнение этой плоскости. Обозначьте произвольную точку, лежащую на плоскости, буквой L, пусть у нее будут координаты (x;y;z). Теперь рассмотрите три вектора PK, PM и PL, они лежат на одной плоскости (компланарны), поэтому их смешанное произведение равно нулю.
Найдите координаты векторов PK, PM и PL:
PK = (xk-xp;yk-yp;zk-zp)
PM = (xm-xp;ym-yp;zm-zp)
PL = (x-xp;y-yp;z-zp)
Смешанное произведение этих векторов будет равно определителю, представленному на рисунке. Этот определитель следует вычислить, чтобы найти уравнение для плоскости. Вычисление смешанного произведения для конкретного случая смотрите в примере.
Пример
Пусть плоскость задана тремя точками K(2;1;-2), M(0;0;-1) и P(1;8;1). Требуется найти нормальный вектор плоскости.
Возьмите произвольную точку L с координатами (x;y;z). Вычислите векторы PK, PM и PL:
PK = (2-1;1-8;-2-1) = (1;-7;-3)
PM = (0-1;0-8;-1-1) = (-1;-8;-2)
PL = (x-1;y-8;z-1)
Составьте определитель для смешанного произведения векторов (он на рисунке).
Теперь разложите определитель по первой строке, а затем подсчитайте значения определителей размера 2 на 2.
Таким образом уравнение плоскости -10x + 5y — 15z — 15 = 0 или, что то же, -2x + y — 3z — 3 = 0. Отсюда легко определить вектор нормали к плоскости: n = (-2;1;-3).
Источники:
- Уравнение плоскости, проходящей через три точки
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
есть 3 точки нужно найти нормаль плоскости в которой они лежат
-
Вопрос заданболее года назад
-
1577 просмотров
1
комментарий
Решения вопроса 1
@Rsa97
Для правильного вопроса надо знать половину ответа
Нормаль к плоскости вычисляется как векторное произведение двух векторов, задающих плоскость. Для точек A, B, C можно взять векторы AB и AC.
Комментировать
Пригласить эксперта
Ответы на вопрос 1
@samodum
Какой вопрос — такой и ответ
Похожие вопросы
-
Показать ещё
Загружается…
25 мая 2023, в 12:25
2000 руб./в час
25 мая 2023, в 12:09
3000 руб./за проект
25 мая 2023, в 11:42
1000 руб./за проект
Минуточку внимания
Как нормировать вектор
wikiHow работает по принципу вики, а это значит, что многие наши статьи написаны несколькими авторами. При создании этой статьи над ее редактированием и улучшением работали авторы-волонтеры.
Количество просмотров этой статьи: 21 763.
Вектор является геометрическим объектом, он характеризуется направлением и величиной. Его можно представить в виде отрезка с начальной точкой на одном конце и стрелкой на втором, при этом длина отрезка соответствует величине вектора, а стрелка указывает на его направление. Нормирование вектора является стандартной операцией в математике, на практике она используется в компьютерной графике.
Вектор нормали: расчет и пример
В нормальный вектор Он определяет направление, перпендикулярное рассматриваемому геометрическому объекту, который может быть, например, кривой, плоскостью или поверхностью.
Это очень полезная концепция для позиционирования движущейся частицы или какой-либо поверхности в пространстве. На следующем графике можно увидеть, как вектор нормали к произвольной кривой C:
Рассмотрим точку P на кривой C. Точка может представлять движущуюся частицу, которая движется по траектории C. Касательная линия к кривой в точке P нарисована красным.
Обратите внимание, что вектор Т касается C в каждой точке, а вектор N перпендикулярно Т y указывает на центр воображаемого круга, дуга которого является сегментом C. Векторы выделены жирным шрифтом в печатном тексте, чтобы отличать их от других не векторных величин.
Вектор Т он всегда указывает, куда движется частица, следовательно, указывает ее скорость. Вместо вектора N всегда указывает в том направлении, в котором вращается частица, отмечая, таким образом, вогнутость кривой C.
Как получить вектор нормали к плоскости?
Вектор нормали не обязательно является единичным вектором, то есть вектором с модулем 1, но если это так, он называется нормальный единичный вектор.
Во многих приложениях необходимо знать вектор нормали к плоскости вместо кривой. Этот вектор показывает ориентацию указанной плоскости в пространстве. Например, рассмотрим самолет п (желтый) рисунка:
К этой плоскости есть два нормальных вектора: п1 Y п2. Использование того или другого будет зависеть от контекста, в котором находится упомянутый самолет. Получить вектор нормали к плоскости очень просто, если вы знаете его уравнение:
ах + по + cz + d = 0, с участием к, б, c Y d вещественные числа.
Ну, нормальный вектор к указанной плоскости задается следующим образом:
N = а я + b j + c k
Здесь вектор N Он выражается через единичные векторы и перпендикулярно друг другу. я, j Y k, направленных по трем направлениям, определяющим пространство X и Zсм. рисунок 2 справа.
Вектор нормали из векторного произведения
Очень простая процедура нахождения вектора нормали использует свойства векторного произведения между двумя векторами.
Как известно, три разные точки, не лежащие на одной прямой, определяют плоскость Р. Теперь можно получить два вектора или Y v которые принадлежат упомянутой плоскости, имеющей эти три точки.
Когда у вас есть векторы, векторный продуктили Икс v — операция, результатом которой, в свою очередь, является вектор, который имеет свойство быть перпендикулярным плоскости, определяемой или Y v.
Известный этот вектор, он обозначается как N, и из него можно будет определить уравнение плоскости благодаря уравнению, указанному в предыдущем разделе:
N = или Икс v
На следующем рисунке показана описанная процедура:
пример
Найти уравнение плоскости, определяемой точками A (2,1,3); В (0,1,1); С (4.2.1).
Решение
Это упражнение иллюстрирует описанную выше процедуру. Имея 3 точки, одна из них выбирается как общее начало двух векторов, которые принадлежат плоскости, определенной этими точками. Например, точка A устанавливается в качестве начала координат и строятся векторы AB Y AC.
Вектор AB — вектор, начало которого — точка A, а конец — точка B. Координаты вектора AB определяются соответственно вычитанием координат B из координат A:
AB = (0-2) я + (1-1) j + (1-3) k = -2я + 0j -2 k
Таким же образом поступаем и находим вектор AC:
AC = (4-2) я + (2-1) j + (1-3) k = 2я + j -2 k
Расчет векторного произведения AB x AC
Существует несколько процедур для нахождения векторного произведения между двумя векторами. В этом примере используется мнемоническая процедура, которая использует следующий рисунок для поиска векторных произведений между единичными векторами. я, j Y k:
Для начала следует помнить, что векторные произведения между параллельными векторами равны нулю, поэтому:
я Икс я = 0; j Икс j = 0; k Икс k = 0
А поскольку векторное произведение — это еще один вектор, перпендикулярный участвующим векторам, двигаясь в направлении красной стрелки, мы имеем:
я Икс j = k ; j Икс k = я; k Икс я = j
Если вам нужно двигаться в направлении, противоположном стрелке, добавьте знак (-):
j Икс я = – k; k Икс j = –я; я Икс k = –j
Всего можно составить 9 векторных произведений с единичными векторами. я, j Y k, из которых 3 будут нулевыми.
AB Икс AC = (-2я + 0j -2 k) х (2я + j -2 k)= -4(я Икс я) -2(я Икс j)+4 (я Икс k)+0 (j Икс я) + 0 (j Икс j) – 0 (j Икс k) – 4 (k Икс я)-2 (k Икс j) + 4 (k Икс k) = -2k-4j-4j+2я = 2я -8j-2k
Уравнение плоскости
Вектор N был определен с помощью предварительно рассчитанного векторного произведения:
N = 2я -8j-2k
Следовательно, a = 2, b = -8, c = -2, искомая плоскость:
ах + по + cz + d = 0 → 2x-8y-2z + d = 0
Значение d. Это легко сделать, если значения любой из имеющихся точек A, B или C подставить в уравнение плоскости. Выбор C, например:
2,4 — 8,2 — 2,1 + d = 0
Вкратце, искомая карта:
Пытливый читатель может задаться вопросом, был бы такой же результат, если бы вместо выполнения AB Икс AC они бы предпочли произвести AC Икс AB. Ответ: да, плоскость, определяемая этими тремя точками, уникальна и имеет два вектора нормали, как показано на рисунке 2.
Что касается точки, выбранной в качестве исходной точки векторов, нет проблем с выбором любого из двух других.
Векторы в пространстве и метод координат
Первый — классический — требует отличного знания аксиом и теорем стереометрии, логики, умения построить чертеж и свести объемную задачу к планиметрической. Способ хорош тем, что развивает мозги и пространственное воображение.
Другой метод — применение векторов и координат. Это простые формулы, алгоритмы и правила. Он очень удобен, особенно когда времени до экзамена мало, а решить задачу хочется.
Если вы освоили векторы на плоскости и действия с ними — то и с векторами в пространстве разберетесь. Многие понятия окажутся знакомыми.
Система координат в пространстве
Выберем начало координат. Проведем три взаимно перпендикулярные оси X, Y и Z. Зададим удобный масштаб.
Получилась система координат в трехмерном пространстве. Теперь каждая его точка характеризуется тремя числами — координатами по X, Y и Z. Например, запись M(−1; 3; 2) означает, что координата точки M по X (абсцисса) равна −1, координата по Y (ордината) равна 3, а координата по Z (аппликата) равна 2.
Векторы в пространстве определяются так же, как и на плоскости. Это направленные отрезки, имеющие начало и конец. Только в пространстве вектор задается тремя координатами x, y и z:
Как найти координаты вектора? Как и на плоскости — из координаты конца вычитаем координату начала.
Длина вектора в пространстве – это расстояние между точками A и B. Находится как корень квадратный из суммы квадратов координат вектора.
Пусть точка M – середина отрезка AB. Ее координаты находятся по формуле:
Для сложения векторов применяем уже знакомые правило треугольника и правило параллелограмма
Сумма векторов, их разность, произведение вектора на число и скалярное произведение векторов определяются так же, как и на плоскости. Только координат не две, а три. Возьмем векторы />и />.
Произведение вектора на число:
Скалярное произведение векторов:
Косинус угла между векторами:
Последняя формула удобна для нахождения угла между прямыми в пространстве. Особенно если эти прямые – скрещиваются. Напомним, что так называются прямые, которые не параллельны и не пересекаются. Они лежат в параллельных плоскостях.
1. В кубе ABCDA1B1C1D1 точки E и K — середины ребер соответственно A1B1 и B1C1. Найдите косинус угла между прямыми AE и BK.
Если вам достался куб — значит, повезло. Он отлично вписывается в прямоугольную систему координат. Строим чертеж:
Длина ребра куба не дана. Какой бы она ни была, угол между AE и BK от нее не зависит. Поэтому возьмем единичный куб, все ребра которого равны 1.
Прямые AE и BK — скрещиваются. Найдем угол между векторами />и />. Для этого нужны их координаты.
Запишем координаты векторов:
и найдем косинус угла между векторами />и />:
2. В правильной четырехугольной пирамиде SABCD, все ребра которой равны 1, точки E, K — середины ребер SB и SC соответственно. Найдите косинус угла между прямыми AE и BK.
Лучше всего выбрать начало координат в центре основания пирамиды, а оси X и Y сделать параллельными сторонам основания.
Координаты точек A, B и C найти легко:
Из прямоугольного треугольника AOS найдем
Координаты вершины пирамиды:
Точка E — середина SB, а K — середина SC. Воспользуемся формулой для координат середины отрезка и найдем координаты точек E и K.
Найдем координаты векторов и
и угол между ними:
Покажем теперь, как вписать систему координат в треугольную призму:
3. В правильной треугольной призме ABCA1B1C1, все ребра которой равны 1, точка D — середина ребра A1B1. Найдите косинус угла между прямыми AD и BC1
Пусть точка A — начало координат. Возьмем ось X параллельно стороне BC, а ось Y перпендикулярно ей. Другими словами, на оси Y будет лежать отрезок AH, являющийся высотой треугольника ABC. Нарисуем отдельно нижнее основание призмы.
Запишем координаты точек:
Точка D — середина A1B1. Значит, пользуемся формулами для координат середины
отрезка.
Найдем координаты векторов />и />, а затем угол между ними:
Смотрите, как легко с помощью векторов и координат найти угол между прямыми. А если требуется найти угол между плоскостями или между прямой и плоскостью? Для решения подобных задач нам понадобится уравнение плоскости в пространстве.
Плоскость в пространстве задается уравнением:
Здесь числа A, B и C — координаты вектора, перпендикулярного этой плоскости. Его называют нормалью к плоскости.
Вместо x, y и z можно подставить в уравнение координаты любой точки, принадлежащей данной плоскости. Получится верное равенство.
Плоскость в пространстве можно провести через любые три точки, не лежащие на одной прямой. Поэтому для того, чтобы написать уравнение плоскости, берем координаты трех принадлежащих ей точек. Подставляем их по очереди в уравнение плоскости. Решаем полученную систему.
Покажем, как это делается.
Напишем уравнение плоскости, проходящей через точки M (1; 0; 1), N (2; −2; 0) и K (4; 1; 2).
Уравнение плоскости выглядит так:
Подставим в него по очереди координаты точек M, N и K.
То есть A + C + D = 0.
Аналогично для точки K:
Получили систему из трех уравнений:
В ней четыре неизвестных: A, B, C и D. Поэтому одну из них мы выберем сами, а другие выразим через нее. Правило простое — вместо одной из переменных можно взять любое число, не равное нулю.
Пусть, например, D = −2. Тогда:
Выразим C и B через A и подставим в третье уравнение:
Решив систему, получим:
Уравнение плоскости MNK имеет вид:
Умножим обе части уравнения на −3. Тогда коэффициенты станут целыми:
Вектор — это нормаль к плоскости MNK.
Уравнение плоскости, проходящей через заданную точку имеет вид:
Угол между плоскостями равен углу между нормалями к этим плоскостям:
Не правда ли, знакомая формула? Скалярное произведение нормалей поделили на произведение их длин.
Заметим, что при пересечении двух плоскостей вообще-то образуется четыре угла.
Мы берем меньший из них. Поэтому в формуле стоит модуль скалярного произведения — чтобы косинус угла был неотрицателен.
4. В кубе ABCDA1B1C1D1 точки E и F — середины ребер соответственно A1B1 и A1D1. Найдите тангенс угла между плоскостями AEF и BDD1.
Строим чертеж. Видно, что плоскости AEF и BDD1 пересекаются где-то вне куба. В классическом решении пришлось бы строить линию их пересечения. Но векторно-координатный метод значительно всё упрощает. Не будем ломать голову над тем, по какой прямой пересекаются плоскости. Просто отметим координаты нужных нам точек и найдем угол между нормалями к плоскостям AEF и BDD1.
Сначала — нормаль к плоскости BDD1. Конечно, мы можем подставить координаты точек B, D и D1 в уравнение плоскости и найти коэффициенты, которые и будут координатами вектора нормали. А можем сделать хитрее — увидеть нужную нормаль прямо на чертеже. Ведь плоскость BDD1 — это диагональное сечение куба. Вектор перпендикулярен этой плоскости.
Итак, первый вектор нормали у нас уже есть:
Напишем уравнение плоскости AEF.
Берем уравнение плоскости и по очереди подставляем в него, вместо x, y и z, соответствующие координаты точек A, E и F.
Пусть С = -1. Тогда A = B = 2.
Уравнение плоскости AEF:
Нормаль к плоскости AEF:
Найдем угол между плоскостями:
5. Основание прямой четырехугольной призмы BCDA1B1C1D1 — прямоугольник ABCD, в котором AB = 5, AD = √33. Найдите тангенс угла между плоскостью грани AA1D1D и плоскостью, проходящей через середину ребра CD перпендикулярно прямой B1D, если расстояние между прямыми A1C1 и BD равно √3.
Эта задача наглядно показывает, насколько векторный метод проще классического. Попробуйте, для разнообразия, построить необходимые сечения и провести все доказательства — как это делается в «классике» 🙂
Строим чертеж. Прямую четырехугольную призму можно по-другому назвать «параллелепипед».
Замечаем, что длина и ширина параллелепипеда у нас есть, а вот высота — вроде не дана. Как же ее найти?
«Расстояние между прямыми A1C1 и BD равно √3». Прямые A1C1 и BD скрещиваются. Одна из них — диагональ верхнего основания, другая — диагональ нижнего. Вспомним, что расстояние между скрещивающимися прямыми равно длине их общего перпендикуляра. Общий перпендикуляр к A1C1 и BD — это, очевидно, OO1, где O — точка пересечения диагоналей нижнего основания, O1 — точка пересечения диагоналей верхнего. А отрезок OO1 и равен высоте параллелепипеда.
Плоскость AA1 D1 D — это задняя грань призмы на нашем чертеже. Нормаль к ней — это любой вектор, перпендикулярный задней грани, например, вектор />или, еще проще, вектор />.
Осталась еще «плоскость, проходящая через середину ребра CD перпендикулярно прямой B1D». Но позвольте, если плоскость перпендикулярна прямой B1D — значит, B1D и есть нормаль к этой плоскости! Координаты точек B1 и D известны:
Координаты вектора — тоже:
Находим угол между плоскостями, равный углу между нормалями к ним:
Зная косинус угла, находим его тангенс по формуле
Угол между прямой m и плоскостью α тоже вычисляется с помощью скалярного произведения векторов.
Пусть — вектор, лежащий на прямой m (или параллельный ей), — нормаль к плоскости α.
Находим синус угла между прямой m и плоскостью α по формуле:
6. В кубе ABCDA1B1C1D1 точка E — середина ребра A1B1. Найдите синус угла между прямой AE и плоскостью BDD1.
Как всегда, рисуем чертеж и выбираем систему координат
Находим координаты вектора .
Нужно ли нам уравнение плоскости BDD1? В общем-то, без него можно обойтись. Ведь эта плоскость является диагональным сечением куба, а значит, нормалью к ней будет любой вектор, ей перпендикулярный. Например, вектор .
Найдем угол между прямой и плоскостью:
Расстояние от точки M с координатами x0, y0 и z0 до плоскости α, заданной уравнением Ax + By + Cz + D = 0, можно найти по формуле:
7. В основании прямоугольного параллелепипеда BCDA1B1C1D1 лежит прямоугольник ABCD со сторонами AB = , AD = . Высота параллелепипеда AA1 = . Найдите расстояние от точки A до плоскости A1DB.
Построим чертеж и выпишем координаты точек:
Запишем уравнение плоскости A1DB. Вы помните, как это делается — по очереди подставляем координаты точек A1, D и B в уравнение Ax + Be + Cz + D
Решим эту систему. Выберем
Уравнение плоскости A1DB имеет вид:
Дальше все просто. Находим расстояние от точки A до плоскости A1DB:
В некоторых задачах по стереометрии требуется найти расстояние от прямой до параллельной ей плоскости. В этом случае можно выбрать любую точку, принадлежащую данной прямой.
Щебетун Виктор
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Для начала стоит напомнить, как выглядит общее уравнение плоскости:
$Ax cdot + By + Cz + D = 0left(1right)$,
при этом: ${A; B; C}$ — координаты нормального вектора данной плоскости, а $D$ — свободный член.
В общем уравнении коэффициенты $A, B, C$ не могут быть одновременно равны нулю, если же один из коэффициентов нулевой — уравнение называется неполным. При $D=0$ плоскость проходит через центр осей координат.
Также в дальнейшем нам пригодится уравнение плоскости, заданной точкой, лежащей в данной плоскости и нормальным вектором:
$A(x-x_0)+B(y-y_0) + C(z-z_0)=0left(2right)$,
здесь $(x_0; y_0; z_0)$ — координаты точки плоскости.
Теперь непосредственно к делу.
Уравнение плоскости через три точки можно выразить несколькими способами: с помощью смешанного произведения векторов и выразив сначала нормальный вектор плоскости и используя одну точку.
Сдай на права пока
учишься в ВУЗе
Вся теория в удобном приложении. Выбери инструктора и начни заниматься!
Получить скидку 3 000 ₽
Уравнение плоскости, проходящей через 3 точки, через смешанное произведение векторов
Рассмотрим три точки $M_1, M_2, M_3$, не находящиеся на одной прямой. Соответственно аксиоме стереометрии о том, что три точки задают плоскость, и притом только одну, все эти точки лежат в одной плоскости $α$.
Рисунок 1. Плоскость через 3 точки. Автор24 — интернет-биржа студенческих работ
Рассмотрим точку $M$, лежащую в плоскости $α$. Если описать плоскость $α$ как множество точек $M$, вектора $vec{M_1M_2}$, $vec{M_1M_3}$ и $vec{M_1M}$ должны быть компланарны между собой. А как известно, вектора компланарны между собой если их смешанное произведение равно нулю.
Соответственно, для того чтобы вычислить это смешанное произведение, необходимо вычислить определитель третьего порядка, каждая строка которого является координатами вышеперечисленных векторов.
«Уравнение плоскости через 3 точки» 👇
Пусть координаты точек $M, M_1, M_2, M_3$ — $(x; y; z), (x_1;y_1; z_1), (x_2;y_2; z_2), (x_3;y_3;z_3)$ соответственно. Тогда координаты каждого из вышеперечисленных векторов составят:
$vec{M_1M_2}={x_2-x_1; y_2-y_1; z_2-z_1}$;
$vec{M_1M_3}= {x_3-x_1; y_3-y_1; z_3-z_1}$;
$vec{M_1M} = {x-x_1; y-y_1; z-z_1}$.
Составим определитель, описывающий смешанное произведение векторов:
$begin{array}{|ccc|} x-x_1 && y-y_1 && z-z_1 \ x_2-x_1 && y_2-y_1 && z_2-z_1 \ x_3-x_1 && y_3-y_1 &&z_3-z_1 \ end{array}=0$ — уравнение плоскости через 3 точки.
При вычислении этого определителя получается общее уравнение плоскости, проходящей через три точки. Это можно увидеть, раскрыв определитель по первой строке:
$begin{array}{|cc|} y_2-y_1 && z_2-z_1 \ y_3-y_1 &&z_3-z_1 \ end{array} cdot ( x-x_1) + begin{array}{|cc|} x_2-x_1 && z_2-z_1 \ x_3-x_1 &&z_3-z_1 \ end{array} cdot (y-y_1) + begin{array}{|cc|} x_2-x_1 && y_2-y_1 \ x_3-x_1 && y_3-y_1 \ end{array} cdot (z-z_1) = 0left(3right)$.
Коэффициенты из уравнения $(3)$ также совпадают с координатами векторного произведения $vec{M_1M_2}×vec{M_1M_3}$ и, так как два этих вектора неколлинеарны и параллельны рассматриваемой плоскости $α$, данное векторное произведение представляет собой нормальный вектор к плоскости, для которой составляется уравнение.
Уравнение плоскости, заданной 3 точками, через нормальный вектор и точку
Другим альтернативным методом задания плоскости является использование нормального вектора плоскости и точки, принадлежащей данной плоскости.
Для того чтобы воспользоваться данным методом, найдём векторное произведение векторов $vec{M_1M_2}$ и $vec{M_1M_3}$:
$[vec{M_1M_2} × vec{M_1M_3}]= begin{array}{|ccc|} vec{i} &&vec{j} &&vec{k} \ x_2-x_1 &&y_2-y_1 &&z_2-z_1 \ x_3-x_1 &&y_3-y_1 &&z_3-z_1 \ end{array}=0$.
Данное произведение является нормальным вектором плоскости, для которой составляется уравнение. Полученные координаты нормального вектора можно использовать непосредственно для составления уравнения плоскости.
Зная точку, принадлежащую этой плоскости, можно подставить координаты нормального вектора и координаты точки в уравнение $(2)$ и получить уравнение плоскости:
$n_x(x-x_3)+n_y(y-y_3)+n_z(z-z_3)=0$.
В этом уравнении $n_x; n_y; n_z$ — координаты нормального вектора, определённого из векторного произведения векторов $vec{M_1M_2}$ и $vec{M_1M_3}$, а $(x_3; y_3; z_3)$ — некая точка, принадлежащая данной плоскости.
Замечание 1
По сути, два вышеприведённых метода представляют одно и то же, так как в обоих необходимо найти координаты нормального вектора и затем, используя их и координаты третьей неиспользованной точки, получить уравнение самой плоскости.
К данной задаче можно также свести задачу с нахождением уравнения плоскости по уравнениям лежащих в ней параллельных и пересекающихся прямых.
Пример 1
Cоставить уравнение плоскости, проходящей через 3 точки $M_1,M_2, M_3$ c координатами $(1;2;3), (1;2;4)$ и $(4;2;-1)$ соответственно.
Воспользуемся вторым способом и найдём координаты вектора через векторное произведение. Для этого сначала выразим координаты векторов:
$M_1M_2={1-1;2-2;4-3}={0;0;1}$
$M_1M_3={4-1;2-2;-1-3}={3;0;-4}$
Найдём их векторное произведение:
$[vec{M_1M_2} × vec{M_1M_3}]= begin{array}{|ccc|} vec{i} && vec{j} && vec{k} \ 0 &&0 &&1 \ 3 &&0 &&-4 \ end{array}=vec{i} cdot begin{array}{|cc|}\ 0 &&1 \ 0 &&-4 \ end{array} + vec{j} cdot begin{array}{|cc|} \ 0 &&1 \ 3 &&-4 \ end{array} + vec{k} cdot begin{array}{|cc|} \ 0 &&0 \ 3 &&0 \ end{array}=0+(-3) cdot vec{j} + 0 Rightarrow vec{n}={0;-3;0}$.
Подставим координаты нормального вектора в уравнение $(2)$:
$0cdot(x-4)+(-3) cdot (y-2)+0 cdot(z+1)=0$.
$-3y+6=0$ — искомое уравнение плоскости.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме