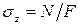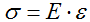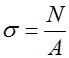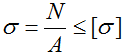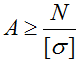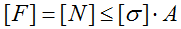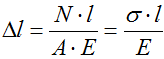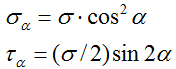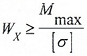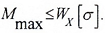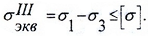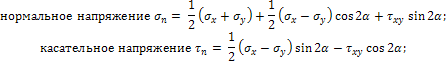Привет! В этом уроке начнём знакомиться с таким видом деформации, как растяжение (сжатие). Обычно, с этой темы и начинают изучать сопротивление материалов — объясняются основные понятия, которые дальше используются на протяжении всего обучения.
Задание, которое будем рассматривать в этой статье, как правило, дается студентам в первую очередь в качестве домашней работы. После изучения материалов этого урока ты научишься строить следующие эпюры: продольных сил, нормальных напряжений, а также осевых перемещений поперечных сечений. Не пугайся мудрёных названий, на самом деле, все эти эпюры строятся очень просто!
Что же давай приступим к изучению!
Построение эпюры продольных сил
В качестве примера возьмём простенькую расчётную схему стержня (также часто ступенчатый стержень, который работает на растяжение или сжатие, называют брусом). Загрузим наш стержень сосредоточенными силами, вот так:

Теперь наша первостепенная задача – построить эпюру продольных сил. И давай сразу будем разбираться в терминологии.
Что такое эпюра?
Эпюра – это график, который принято строить для визуализации распределения какой-либо величины. В нашем случае, продольной силы.
Построив такой график, мы можем увидеть, где определённая величина достигает максимальных или минимальных значений, что может быть полезно при проведении прочностных расчётов и других. Кроме того, эпюры могут служить вспомогательными инструментами для построения других эпюр, о чём мы будем говорить далее.
Что такое продольная сила?
Продольная сила – это внутренняя сила, которая возникает в сечениях стержня, работающего на растяжение или сжатие под действием внешней нагрузки.
Расчёт эпюры продольных сил
Чтобы построить эпюру продольных сил, нужно разбить брус на несколько участков, где эпюра будет иметь постоянное значение. Конкретно, для этого стержня, границами участков служат те точки, где прикладываются сосредоточенные силы.
То есть для нашего примера, нужно рассмотреть всего 2 участка:

Важно! Эпюра продольных сил, никак не зависит от формы бруса, в отличие от других эпюр, которые будем дальше рассчитывать.
Правило знаков для продольных сил
Правило знаков для продольных сил следующее:
- если внешняя сила (F) растягивает брус, то продольная сила (N) в сечениях будет положительная;
- если внешняя сила (F) сжимает брус, то продольная сила (N) в сечениях будет отрицательная.

Расчёт продольных сил на участках
На первом участке сила F1 растягивает брус на величину 5 кН, поэтому на этом участке, продольная сила будет положительной и равной:
Откладываем это значение на графике — эпюре. Эпюры, принято заштриховывать перпендикулярно к нулевой линии, а также указывать знак продольной силы:

На втором же участке, помимо силы F1, также действует сила F2, которая сжимает брус, поэтому в уравнении ее нужно учесть со знаком «минус»:
Откладываем полученное значение на эпюре:

Расчёт реакции в жёсткой заделке
Прежде всего, следует разобраться с тем, что вообще такое реакция. Всё дело в том, что помимо внутренних усилий, возникающих внутри нагруженного элемента конструкции, в том месте, где закреплён этот элемент, также возникают некоторые силы (сила), которые являются реакцией на внешнюю нагрузку и удерживающие эту конструкцию в состоянии статического равновесия.
Например, стул на котором ты сейчас сидишь и давишь на него своим весом, сопротивляется, чтобы удерживать тебя в состоянии равновесия. Если переводить на язык сопромата, твой вес в этом случае это внешняя сила, а сила с которой стул реагирует на твой вес – это реакция опоры, равная по модулю этой силе, но противоположно направленная.
Так и в нашей конструкции, в жёсткой заделке, также возникает реакция! Осталось только научиться — определять эту силу. Так как она должна компенсировать всю нагрузку, которая приложена к стержню, условие равновесия для нашей схемы можно записать так:
То есть, так как система находится в состоянии равновесия, то сумма всех сил, действующих на конструкцию, будет равна нулю.
Из этого условия равновесия и найдём искомую реакцию. Приложим некоторую силу R в месте, где закреплён наш стержень, при этом направить её можно в любую сторону, хоть влево, хоть вправо, главное, чтобы она была направлена горизонтально, так как у нас вся нагрузка, направлена так, то и реакция в заделке будет возникать исключительно — горизонтальная:

Чтобы составить уравнение равновесия, введём продольную ось – x, относительно неё будем составлять это уравнение, при этом силы, которые будут совпадать с положительным направлением оси x, в уравнении будем учитывать с «плюсом», а противоположно направленные с «минусом»:

Находим из этого уравнения реакцию в заделке:
А теперь, давай обсудим, что можем делать с этим теперь. В нашей конкретной задаче реакция может помочь проверить эпюру продольных сил. Если в первом уроке, считали стержень, строго справа налево, то теперь, зная численное значение реакции, можно рассчитать стержень и слева направо. Или как минимум увидеть, что левый участок эпюры, был построен верно.
Да, можно было вполне обойтись, без расчёта этой реакции конкретно в этом случае. Но, чаще всего, решение задач по сопромату начинается как раз с определения реакций, потому что без этого в большинстве случаев, невозможно определить внутренние усилия, а тем самым произвести какие-либо дальнейшие расчёты. Но с этим мы ещё многократно будем сталкиваться в следующих уроках, особенно в задачах на изгиб.
Построение эпюры нормальных напряжений
В отличие от продольных сил, нормальные напряжения уже зависят от формы бруса, а если точнее, то от площади его поперечных сечений.
Формула для определения нормальных напряжений выглядит так:

Таким образом, чтобы найти нормальное напряжение в любом сечении бруса, нужно: продольную силу в этом сечении разделить на площадь сечения.
Нормальные напряжения, как и продольные силы, изменяются по одному закону в пределах участков. Однако, так как форма бруса сказывается на распределении нормальных напряжений, здесь границами участков также служат места изменения геометрии бруса. Таким образом, для нашей расчетной схемы, нужно рассмотреть три участка и вычислить напряжения, соответственно, 3 раза:

Будем считать, что по условию задачи нам известны все параметры бруса, включая площади поперечных сечений: на первом участке площадь поперечного сечения A1=2 см2, а на втором и третьем A2 = A3 = 4 см2.

Вычисляем напряжения на каждом участке:

По полученным значениям строим эпюру нормальных напряжений:

По полученной эпюре нормальных напряжений, можно определить те поперечные сечения, в которых напряжения будут максимальными (все сечения на участке 1), что полезно при проведении прочностного расчёта.
Построение эпюры осевых перемещений поперечных сечений
Под действием внешней нагрузки поперечные сечения бруса перемещаются вдоль продольной оси. Под нагрузкой брус может как удлиниться, так и укоротиться. И в этом разделе будем учиться определять эти перемещения.
Для начала подготовимся к расчету и расставим точки в характерных сечениях. Чтобы потом к ним привязываться по ходу решения:

Если для первых двух эпюр, расчет начинался справа налево, от свободного конца. То здесь нам нужно начать считать с закрепленного конца, с жесткой заделки и так как сечение A, закреплено жестко, то никакие перемещения этого сечения невозможны, поэтому сразу можем записать:
Эпюра перемещений так же, как и остальные эпюры, меняется по одному закону, в пределах участков. Поэтому, чтобы построить эпюру, достаточно определить эти перемещения в характерных точках.
Перемещение точки B будет складываться из перемещения предыдущего расчетного сечения:
А также удлинения (или укорочения) участка между расчетными сечениями:
В свою очередь, удлинение (или укорочение) любого участка, можно определить по следующей формуле:

Поэтому формулу, для нахождения перемещения сечения B, можно записать и в другом виде:

Подставив все численные значения, найдем искомое перемещение:

Откладываем полученное значение на эпюре:

Также важно отметить, что при вычислении удлинения или укорочения участка (Δl), фактически площадь эпюры продольных сил (ω) делится на жесткость при растяжении или сжатии (EA).


Это свойство нам еще пригодится, когда будем рассматривать более сложную задачу.
Для точек C и D перемещения находятся аналогичным способом, так же как и для точки B, поэтому подробно комментировать не буду, приведу решение.
Точка C

Точка D

Откладываем полученные значения на эпюре:

По полученной эпюре, можно увидеть — в какую сторону и насколько переместится любое поперечное сечение стержня. Наиболее интересной характеристикой здесь является перемещение сечения D, то есть перемещение свободного конца бруса или фактическое удлинение. Как видим, сечение D переместится вправо на величину WD (т. к. значение WD — положительное). То есть, под действием всей нагрузки брус удлинится на 0.575 мм.
Учёт распределённой нагрузки
А теперь предлагаю рассмотреть немного измененную задачу. Приложим к нашему брусу дополнительно распределенную нагрузку q с интенсивностью равной 2 кН/м. После чего рассчитаем и построим все те же эпюры: продольных сил, нормальных напряжений и перемещений.

Чтобы учесть распределенную нагрузку, необходимо интенсивность нагрузки (q) умножить на длину участка, на котором действует нагрузка. В чистом виде, только от распределенной нагрузки, эпюра продольных сил будет треугольная.

Расчет продольных сил
На первом участке, сила по-прежнему растягивает стержень, записываем ее в уравнение с «плюсом», а распределенная нагрузка сжимает, соответственно, ее учитываем с «минусом»:
Найдем значения продольной силы на границах первого участка:

Откладываем рассчитанные значения:

На втором участке, распределенная нагрузка будет действовать точно так же, как и сосредоточенная сила:
Рассчитываем продольную силу на третьем участке:
Строим окончательную эпюру продольных сил:

Расчет нормальных напряжений
Нормальные напряжения рассчитываются точно так же, как и для первой задачи, единственное отличие только в том, что на первом участке необходимо рассчитать напряжения два раза — на границах участка:

По полученным значениям строим эпюру нормальных напряжений:

Расчет перемещений
Для точек A, B и С перемещения рассчитываются аналогично, как в первой задаче:


Строим эпюру перемещений на втором и третьем участке:

Чтобы рассчитать удлинение на первом участке, нужно вычислить площадь эпюры продольных сил на этом участке и разделить на жесткость (EA):


Так как на этом участке, эпюра состоит из двух одинаковых прямоугольных треугольников, но по разные стороны от нулевой линии, с учетом знаков, ожидаемо, получим, что перемещение точки D, будет равно перемещению точки C.



Однако, необходимо учесть еще одну особенность. На участках, где действуют распределенные нагрузки, эпюры перемещений изменяются не по линейному закону, а по квадратичному.
То есть на участке с распределенной нагрузкой, эпюра перемещений всегда будет иметь либо выпуклость, либо вогнутость:

Чтобы понять, как же будет выглядеть эпюра перемещений, на участке с распределённой нагрузкой, нужно проанализировать эпюру продольных сил.
Как видим, начиная от точки C и до пересечения нулевой линии, эпюра продольных сил – отрицательна, а это значит, что эпюра перемещений, на этом отрезке, также должна убывать, как показано зелёной пунктирной линией. Поэтому изображаем эпюру перемещений следующим образом:

Но чтобы окончательно убедиться в верности наших рассуждений, можно также определить экстремум на эпюре перемещений (там, где эпюра достигает своего максимального значения). Или в той точке, где эпюра продольных сил пересекает нулевую линию:


Отмечаем найденное значение на эпюре перемещений:

Распределение и формула нормальных напряжений
Из гипотезы плоских сечений следует: все продольные волокна стержня деформируются одинаково. Поэтому можно считать, что при растяжении (сжатии) напряжения во всех точках поперечного сечения стержня одинаковы и направлены по нормали к сечению. Такие напряжения, как уже отмечалось, называются нормальными напряжениями.
Из вышеизложенного вытекает формула нормальных напряжений при растяжении (сжатии):
где N – продольное усилие, возникающее в данном поперечном сечении стержня, а F – площадь этого поперечного сечения.
Правило знаков для нормального напряжения (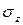
Как определить нормальное напряжение?
Автор: Константин Вавилов · Опубликовано 02.02.2016 · Обновлено 28.11.2017
Сегодня будем говорить о том, как определить нормальное напряжение при растяжении (сжатии). Долго говорить не придется, так как определяется оно элементарно.
Формула для нахождения нормального напряжения следующая:
То есть это отношение продольной силы (N) к площади поперечного сечения (A), на которой действует эта сила.
Пример определение нормальных напряжений
Посмотрим, как на практике пользоваться этой формулой. Например, возьмем брус с постоянным поперечным сечением, на который действует кучка внешних сил. Вас просят найти максимальное нормальное напряжение, возникающее в поперечных сечениях бруса.
Ваша тактика будет такой: Сначала нужно определить продольные силы и по-хорошему построить эпюру, чтобы видеть наиболее опасное сечение, то есть сечение, в котором внутренняя сила максимальная.
В нашем случае продольную силу берем равной трем килоньютонам и делим на площадь поперечного сечения:
Итого получили максимальное напряжение равное 15 мегапаскалям, что для стального бруса совсем пустяк.
Источник
iSopromat.ru
Подборка формул для расчета элементов и конструкций на растяжение-сжатие и решения задач сопротивления материалов по расчету нормальных напряжений, деформаций и перемещения сечений стержней при продольном нагружении.
Формула для расчета напряжений в поперечном сечении стержня
Расчет минимальной площади поперечного сечения бруса
Расчет допустимой величины внешней растягивающей/сжимающей силы (определение грузоподъемности)
Расчет перемещения сечений
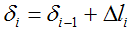
Здесь: δ i — перемещение рассматриваемого сечения,
δ i-1 — перемещение предыдущего сечения,
Δ li — деформация участка между указанными сечениями.
Здесь α — угол отклонения сечения от поперечного.
Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах
Источник
Нормальные напряжения. Формула Навье
Нормальные напряжения. Формула Навье
При изгибе происходит искривление оси балки. При этом часть сечения подвергается деформациям растяжения, другая часть – деформациям сжатия. Между этими частями находится нейтральный слой, продольные деформации в котором равны нулю. Таким образом, при изгибе нейтральный слой не изменяет своей длины.
– продольные волокна не давят друг на друга;
– напряжения и деформации распределяются равномерно по ширине сечения.
Абсолютное удлинение слоя, который находится на расстоянии $y$ от нейтрального слоя
$Delta dx = left( <rho + y>right) cdot dvarphi — rho cdot dvarphi = y cdot dvarphi $.
Относительное удлинение точек на расстоянии $y$ от нейтрального слоя
$varepsilon left( y right) = frac<rho >$ – закон Гука при изгибе.
$sigma = Evarepsilon = Efrac<rho >$.
Таким образом, продольные напряжения и деформации точек балки при изгибе прямо пропорциональны их расстоянию от нейтрального слоя.
При этом неизвестным остается положение нейтрального слоя. Для его определения воспользуемся тем фактом, что при изгибе в сечении не возникает продольной силы ($N = 0$).
$N = intlimits_A^<> sigma ,dA = intlimits_A^<> <rho >> ,dA = frac<rho >intlimits_A^<> y ,dA = frac <rho >cdot = 0$,
где $$ – статический момент площади сечения относительно оси $z$.
Как следствие, $ = 0$, то есть ось $z$ должно быть центральной, то есть нейтральный слой проходит через центральные оси сечений .
Запишем выражение изгибающего момента $$ в сечении в зависимости от напряжений $sigma $. На элементарной площадке $dA$ возникает усилие $dF = sigma dA$. Момент от этого усилия относительно оси $z$ (оси изгиба)
Интегрируем по площади сечения
где $ = intlimits_A <dA> $ – момент инерции сечения относительно оси изгиба.
$E,$ – жесткость сечения при изгибе.
Таким образом, нормальные напряжения при изгибе определяются как
Максимальные нормальные напряжения в сечении будут возникать в наиболее удаленных от оси изгиба точках сечения.
где $ = frac<<>><<>>>$ – момент сопротивления сечения относительно оси изгиба.
Источник
Формулы по сопромату
Приветствую, Вас на проекте — «СопроМат». Эта страничка будет навигатором по самым ходовым формулам сопромата, которые используются при расчетах на прочность, жесткость или устойчивость. Все формулы по сопромату классифицированы по виду деформации: растяжение или сжатие, кручение и изгиб.
Навигация по формулам:
Формулы по теме поперечный изгиб
В рамках этого раздела опубликованы основные формулы по теме «Поперечный изгиб». Также его часто называют простым или прямым изгибом.
Формулы для определения напряжений при поперечном изгибе
Формула для определения нормальных напряжений в точках поперечного сечения:
где Mx — изгибающий момент в поперечном сечении, Ix — момент инерции относительно центральной оси, y — расстояние от центральной оси до точки в которой вычисляется напряжение.
Формула для определения максимального (минимального) нормального напряжения в наиболее опасных точках поперечного сечения:
где Mx — изгибающий момент в поперечном сечении, Wx — момент сопротивления относительно центральной оси.
Формула для определения момента сопротивления поперечного сечения:
где Ix — момент инерции относительно центральной оси, y m ax — расстояние до наиболее удаленных точек поперечного сечения.
Формула для определения касательных напряжений в точках поперечного сечения:
где Q y — поперечная сила в рассматриваемом сечении, S отс — статический момент относительно центральной оси отсеченной части поперечного сечения, Ix — момент инерции относительно центральной оси, b — ширина поперечного сечения на высоте h, где рассчитываются касательные напряжения.
Формула для определения главных напряжений (максимальное и минимальное) при поперечном изгибе:
Источник
iSopromat.ru
Важнейшим критерием оценки прочности балок при изгибе являются напряжения.
Рассмотрим способы расчета напряжений при плоском поперечном изгибе балки
Расчет напряжений
Возникающий в поперечных сечениях при чистом прямом изгибе изгибающий момент Mx 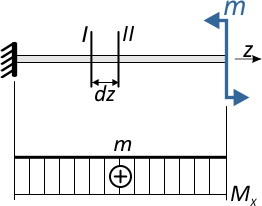
представляет собой равнодействующий момент внутренних нормальных сил, распределенных по сечению и вызывающих нормальные напряжения в точках сечения. 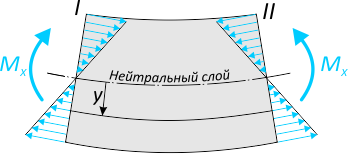
Закон распределения нормальных напряжений по высоте сечения выражается формулой: 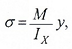
где:
M — изгибающий момент, действующий в рассматриваемом сечении относительно его нейтральной линии X;
Ix — осевой момент инерции поперечного сечения балки относительно нейтральной оси;
y – расстояние от нейтральной оси до точки, в которой определяется напряжение.
Нейтральная ось при изгибе проходит через центр тяжести поперечного сечения.
По вышеуказанной формуле, нормальные напряжения по высоте сечения изменяются по линейному закону.
Наибольшие значения имеют напряжения у верхнего и нижнего краев сечения.
Например, для симметричного относительно нейтральной оси сечения, где y1=y2=h/2: 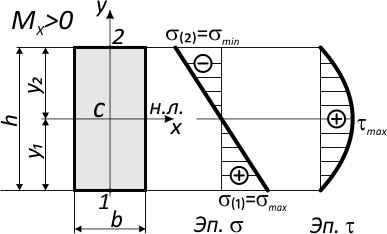
Напряжения в крайних точках по вертикали (точки 1 и 2) равны по величине, но противоположны по знаку. 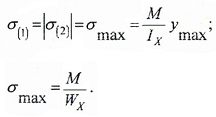
Для несимметричного сечения 
напряжения определяются отдельно для нижней точки 1 и верхней точки 2: 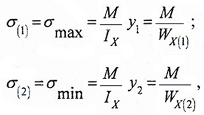
где: 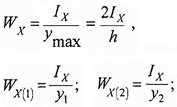
WX — осевой момент сопротивления симметричного сечения;
WX(1) и WX(2) — осевые моменты сопротивления несимметричного сечения для нижних и верхних слоев балки.
Знаки нормальных напряжений при их расчете, рекомендуется определять по физическому смыслу в зависимости от того, растянуты или сжаты рассматриваемые слои балки.
Условия прочности при изгибе
Прочность по нормальным напряжениям
Условие прочности по нормальным напряжениям для балок из пластичного материала записывается в одной крайней точке. 
В случае балки из хрупких материалов, которые, как известно, по-разному сопротивляются растяжению и сжатию – в двух крайних точках сечения. 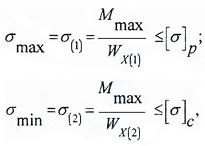
Здесь:
Mmax — максимальное значение изгибающего момента, определяемого по эпюре Mx;
[ σ], [ σ]р, [ σ]с — допустимые значения напряжений для материала балки (для хрупких материалов – на растяжение (р) и сжатие (с)).
Для балки из хрупкого материала обычно применяют сечения, несимметричные относительно нейтральной оси. При этом сечения располагают таким образом, чтобы наиболее удаленная точка сечения размещалась в зоне сжатия, так как [ σ]с>[ σ]р. 
В таких случаях, проверку прочности следует обязательно проводить в двух сечениях: с наибольшим положительным изгибающим моментом и с наибольшим по абсолютной величине (модулю) отрицательным значением изгибающего момента.
При расчете элементов конструкций, работающих на изгиб, с использованием вышеуказанных условий прочности решаются три типа задач:
- Проверка прочности
- Подбор сечений
- Определение максимально допустимой нагрузки
Прочность по касательным напряжениям
В случае прямого поперечного изгиба в сечениях балки, кроме нормальных напряжений σ от изгибающего момента, возникают касательные напряжения τ от поперечной силы Q.
Закон распределения касательных напряжений по высоте сечения выражается формулой Д.И. Журавского 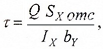
где
Sx отс — статический момент относительно нейтральной оси отсеченной части площади поперечного сечения балки, расположенной выше или ниже точки, в которой определяются касательные напряжения;
by — ширина поперечного сечения балки на уровне рассматриваемой точки, в которой рассчитывается величина касательных напряжений τ.
Условие прочности по касательным напряжениям записывается для сечения с максимальным значением поперечной силы Qmax: 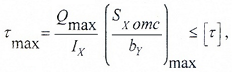
где [ τ] – допустимое значение касательных напряжений для материала балки.
Полная проверка прочности
Полную проверку прочности балки производят в следующей последовательности:
- По максимальным нормальным напряжениям для сечения, в котором возникает наибольший по абсолютному значению изгибающий момент M.
- По максимальным касательным напряжениям для сечения, в котором возникает наибольшая по абсолютному значению поперечная сила Q.
- По главным напряжениям для сечения, в котором изгибающий момент и поперечная сила одновременно достигают значительных величин (или когда Mmax и Qmax действуют в одном и том же сечении балки).
При анализе плоского напряженного состояния главные напряжения при изгибе, примут вид: 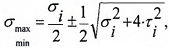
так как нормальные напряжения в поперечном направлении к оси балки принимаются равными нулю.
Проверка прочности осуществляется с помощью соответствующих гипотез прочности, например, гипотезы наибольших касательных напряжений:
Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах
Источник
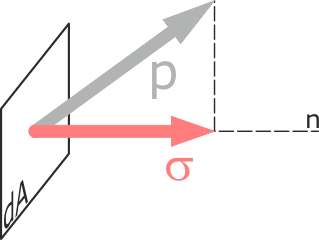
Нормальными напряжениями называют проекции полного напряжения, на нормаль к площадке рассматриваемого элемента.
Т.е. они расположены перпендикулярно (нормально) грани элемента.
- Обозначение – σ (сигма)
- Размерность – Паскаль [Па] и кратные ему, например [МПа]
Главные напряжения являются нормальными.
Нормальные напряжения могут быть как растягивающими так и сжимающими.
Вообще говоря, нормальное напряжение это составляющая полного напряжения p полученная ее проекцией на нормаль к площадке элемента.
Здесь n — нормаль к элементарной площадке.
См. также:
- Примеры расчета напряжений
- Правило знаков для нормальных напряжений
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее
Решение задач и лекции по технической механике, теормеху и сопромату
Напряжением называется
интенсивность действия внутренних сил
в точке тела,
то есть, напряжение — это внутреннее
усилие, приходящееся на единицу площади.
По своей природе напряжение —
это поверхностная
нагрузка,
возникающая на внутренних поверхностях
соприкасания частей тела.
Деформацией называется
изменение размеров и формы тела под
действием приложенных сил.
Напряжением называется
отношение действующего усилия к площади
поперечного сечения тела или образца σ
= P/F.
В
зависимости от направления действия
силы нормальные напряжения подразделяют
на растягивающие и сжимающие.
Различают временные и остаточные напряжения.
Временные
напряжения возникают
под действием внешней нагрузки и исчезают
после ее снятия, остаточные —
остаются в теле после прекращения
действия нагрузки.
Если
после прекращения действия внешних сил
изменения формы, структуры и свойств
тела полностью устраняются, то такая
деформация называется упругой.
При
возрастании напряжений выше предела
упругости деформация становится
необратимой. При снятии нагрузки
устраняется лишь упругая составляющая
деформации, оставшаяся часть
называется пластической
деформацией.
Норм
напряжение:
Составляющая
напряжений, направленных по нормали к
площадке ее действия.
Касат
напряжение:
Составляющая
напряжений, лежащих в плоскости сечения.
Правила
знаков:
Нормальные
напряжения σ принимаются
положительными (т.е. σ>0),
если они растягивают выделенный элемент
бруса.
Касательные
напряжения τ принимаются
положительными (т.е. τ>0),
если они стремятся повернуть рассматриваемый
элемент бруса по ходу часовой стрелки.
При
растяжении-сжатии
Внутренняя
продольная сила N,
которая стремится растянуть рассматриваемую
частьбруса,
считается положительной. Сжимающая
продольная сила имеет отрицательный
знак.
При
кручении
Внутренний
скручивающий момент T считается
положительным, если он стремится
повернуть рассматриваемую часть бруса
против хода часовой стрелки, при взгляде
на него со стороны внешней нормали.
При
изгибе
Внутренняя
поперечная сила Q считается
положительной, в случае, когда она
стремится повернуть рассматриваемую
часть бруса по ходу часовой стрелки.
Внутренний
изгибающий момент M положителен, когда
он стремится сжать верхние волокна
бруса.
Деформация
при растяжении-сжатии Δl считается
положительной, если длина стержняпри
этом увеличивается.
При
плоском поперечном изгибе
Вертикальное
перемещение сечения бруса принимается
положительным, если оно направлено
вверх от начального положения.
Правило
знаков при составлении уравнений статики
—
для проекций сил на оси системы координат
Проекции
внешних сил на оси системы координат
принимаются положительными, если их
направление совпадает с положительным
направлением соответствующей оси.
—
для моментов
Сосредоточенные
моменты и моменты сил в уравнениях
статики записываются с положительным
знаком, если они стремятся повернуть
рассматриваемую систему против хода
часовой стрелки.
Правило
знаков при составлении уравнений статики
для неподвижных систем
При
составлении уравнений равновесия
статичных (неподвижных) систем (например,
приопределении
опорных реакций),
последние два правила упрощаются до
вида:
Проекции
сил и моменты, имеющие одинаковое
направление принимаются положительными,
а соответственно проекции сил и моменты
обратного направления – отрицательными.
ПЛОСКОЕ
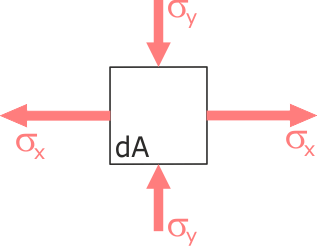
НАПРЯЖЕННОЕ СОСТОЯНИЕ
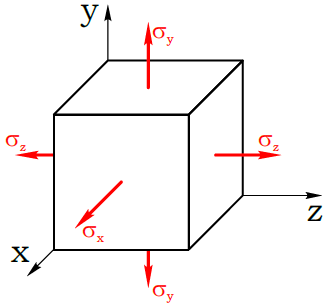
Если
все векторы напряжений параллельны
одной и той же плоскости, напряженное
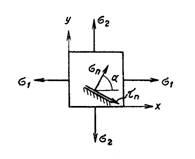
состояние называется плоским (рис. 1).
Иначе: напряженное состояние является
плоским, если одно из трех главных
напряжений равно нулю.
Рисунок
1.
Плоское
напряженное состояние реализуется в
пластине, нагруженной по ее контуру
силами, равнодействующие которых
расположены в ее срединной плоскости
(срединная плоскость — плоскость, делящая
пополам толщину пластины).
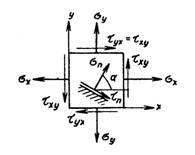
Направления
напряжений на рис. 1 приняты за
положительные. Угол α положителен, если
он откладывается от оси х к оси у. На
площадке с нормалью n:
|
|
(1) |
при .
Нормальное
напряжение σn положительно,
если оно растягивающее. Положительное
напряжение показано
на рис. 1. Правило знаков дляпо
формуле (1) то же самое, что для
напряженийпо
формуле (1).
Данное
здесь правило знаков относится к
наклонным площадкам. В статье «Объёмное
напряженное состояние» сформулировано
правило знаков для компонентов напряжений
в точке, т. е. для напряжений на площадках,
перпендикулярных осям координат. Это
правило знаков принято в теории упругости.
Главные
напряжения на площадках, перпендикулярных
плоскости напряжений:
|
|
(2) |
(Поскольку
здесь рассматриваются только два главных
напряжения, они обозначены через σ1 и
σ2,
хотя может оказаться, что σ2<0,
т. е. σ2 не
будет средним из трех главных напряжений).
Угол α1 составляемый
нормалью к первой главной площадке с
осью х, находится из равенства:
|
|
(3) |
Наибольшее
и наименьшее касательные напряжения
|
|
(4) |
Эти
напряжения действуют на площадках,
расположенных под углом 45° к первой и
второй главным площадкам.
Если
главные напряжения σ1 и
σ2 имеют
одинаковый знак, то наибольшее касательное
напряжение действует на площадке,
расположенной под углом 45° к плоскости
напряжений (плоскости ху). В этом случае:
В
стенке балки (здесь имеется в виду
обычная балка, а не балка-стенка) при
ее изгибе силами реализуется частный
случай плоского напряженного состояния.
В стенках балки одно из нормальных
напряжений σy равно
нулю. В этом случае напряжения получатся
по формулам (1), (2) и (4), если в этих формулах
положить σy=0.
Положение первой главной площадки
определяется формулой (3).
РАСТЯЖЕНИЕ
ПО ДВУМ НАПРАВЛЕНИЯМ (рис
2):
Рисунок
2.
При
σ1>0
и σ2<0
При
σ1>0
и σ2>0
При
σ1<0
и σ2<0
ЧИСТЫЙ
СДВИГ (рис.
3)
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #