Как найти нормаль функции в точке - Avtoru.top - решение различных проблем

Найдем производную, дифференцируя функцию $ y(x) $ по переменной $ x $:

$$ (x^2)’_x+ (2xy^2)’_x + (3y^4)’_x = (6)’_x $$

Учитывая, что $ y^2 $ и $ y^4 $ сложные функции продолжаем:

$$ 2x + 2y^2 + 4xyy’ + 12y^3 y’ = 0 $$

Выражаем $ y’ $ из полученного уравнения:

$$ 4xyy’ + 12y^3 y’ = -2x — 2y^2 $$

Выносим $ y’ $ за скобки:

$$ y'(4xy + 12y^3) = -2x — 2y^2 $$

Делим обе части уравнения на выражение $ 4xy+12y^3 $:

$$ y’ = -frac{2x+2y^2}{4xy + 12y^3} = -frac{x+y^2}{2xy+6y^3} $$

Теперь вычисляем значение $ y’ $:

$$ y’ = -frac{1 + (-1)^2}{2cdot 1 cdot (-1) + 6cdot (-1)^3} = -frac{2}{-8} = frac{1}{4} $$

Зная, что $ y’ = frac{1}{4} $ и $ y(x_0) = y(1) = -1 $ составляем уравнения касательной и нормали к кривой в точке $ M(1;-1) $.

Получаем уравнение касательной:

$$ y — (-1) = frac{1}{4} (x — 1) $$

Записываем в красивой форме:

$$ y = frac{1}{4} x — frac{3}{4} $$

Получаем уравнение нормали:

$$ y — (-1) = -frac{1}{frac{1}{4}} (x — 1) $$

Раскрываем скобки и записываем в красивой форме, полученное уравнение:

$$ y+1 = -4(x-1) $$

$$ y = -4x + 3 $$

Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!

Источник

Вывод уравнения нормали к графику функции

Евгений Николаевич Беляев

Эксперт по предмету «Математика»

Задать вопрос автору статьи

Замечание 1

Нормаль — это прямая, которая образует с касательной к графику функции угол в $90°$.

Рисунок 1. Нормальный перпендикуляр к графику касательной. Автор24 — интернет-биржа студенческих работ

В связи с тем, что нормаль перпендикулярна к касательной, её угловой коэффициент будет величиной, обратной к угловому коэффициенту касательной:

$k_{норм}=- frac{1}{k_{к}}= -1 frac{1}{f’(x_0)}$.

Пользуясь полученным выводом, запишем уравнение нормали к графику функции:

$y – y_0 = — frac{1}{f’(x_0)} cdot (x – x_0) left(1right) $, здесь $x_0$ и $y_0$ — координаты точки для которой строится искомая линия, при этом производная в этой точке $f’(x_0) ≠ 0$.

Порядок действий при поиске уравнения нормальной прямой если задана координата $x_0$:

Вычисляется, чему равен нулевой игрек $y(x_0)$ для функции.
Затем нужно определить производную.
Нужно высчитать затем, чему равен $f’(x)$ в точке $x_0$, найденное значение — коэффициент касательной.
Все найденные значения подставляются в формулу $(1)$.

Напомним также как выглядит само уравнение касательной:

$y – y_0 = f’(x_0) cdot (x – x_0)$.

Пример 1

Найдите уравнение нормали для функции $y=x^2$ в точке $x_0=2$.

Решение:

Производная данной функции составит $y’(x) = 2x$, затем найдём, чему равен наш подопытный кролик-функция в заданной точке $y_0= x^2 = 2^2 = 4$.

Теперь нужно высчитать производную функции в точке $x_0$: $y’(2) = 2 x = 2 cdot 2= 4$.

Все полученные значения расставляем по своим местам в формулу $(1)$:

$y-4=-frac{1}{4} cdot (x – 2)$

Уравнение нормали найдено.

Находи статьи и создавай свой список литературы по ГОСТу

Поиск по теме

Дата последнего обновления статьи: 07.05.2023

Источник

Задание. Найти тангенс угла между кривыми $y=x^2-1$ и
$y=x^3-1$ в точке их пересечения, которая имеет большую абсциссу.

Решение. Вначале найдем точки пересечения графиков заданных функций, для этого совместно разрешим уравнение заданных кривых:

$$begin{array}{c}
left{begin{array}{l}
y_{1}=x^{2}-1 \
y_{2}=x^{3}-1
end{array} Rightarrow x^{2}-1=x^{3}-1 Rightarrow x^{3}-x^{2}=0 Rightarrowright. \
Rightarrow x_{1,2}=0, x_{3}=1
end{array}$$

Таким образом, искомая точка $x=1$.

Далее находим производные заданных функций в найденной точке:

$$begin{array}{c}
y_{1}^{prime}=left(x^{2}-1right)^{prime}=left(x^{2}right)^{prime}-(1)^{prime}=2 x-0=2 x, y_{1}^{prime}(1)=2 \
y_{2}^{prime}=left(x^{3}-1right)^{prime}=left(x^{3}right)^{prime}-(1)^{prime}=3 x^{2}-0=3 x^{2}, y_{2}^{prime}(1)=3
end{array}$$

Итак, искомый тангенс:

$$operatorname{tg} phi=frac{3-2}{1+2 cdot 3}=frac{1}{7}$$

Ответ. $operatorname{tg} phi=frac{1}{7}$

Источник

Онлайн калькуляторы

На нашем сайте собрано более 100 бесплатных онлайн калькуляторов по математике, геометрии и физике.

Справочник

Основные формулы, таблицы и теоремы для учащихся. Все что нужно, чтобы сделать домашнее задание!

Заказать решение

Не можете решить контрольную?!
Мы поможем! Более 20 000 авторов выполнят вашу работу от 100 руб!

Уравнение нормали

Определение и уравнение нормали

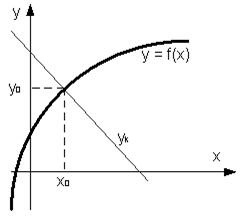
Уравнение нормали имеет вид:

$[y-y_{0} =-frac{1}{f'left(x_{0} right)} left(x-x_{0} right),; y_{0} =yleft(x_{0} right)]$

В случае параметрического задания функции $left{begin{array}{l} {x=xleft(tright),} \ {y=yleft(tright),} end{array}right.$ нормаль задается уравнением: