Как найти неопределенный интеграл 5dx - Avtoru.top

Заказать задачи по любым предметам можно здесь от 10 минут

Онлайн калькулятор неопределенного интеграла

Неопределенные интегралы отличаются от определенных тем, что не заданы пределы интегрирования. Поэтому ответ записывается в аналитическом виде. Данный онлайн калькулятор решает неопределенный интеграл в символьной форме, что отлично помогает студенту проверить правильность ответа своего решения и исправить все ошибки в случае необходимости.

Введите функцию

Пределы интегрирования (необязательно)
от a = до b =

Пример 1 Пример 2 Правила ввода

Пример 1

Вычислить интеграл: $ int x^3 dx $

Решение

Подынтегральная функция представляет собой показательную функцию. В таблице интегрирования находит формулу: $$ int x^p dx = frac{x^{p+1}}{p+1} $$

Ищем аналогию и делаем вывод о том, что к степени нужно прибавить единицу, а затем полученную функцию разделить на эту же степень.

$$ int x^3 dx = frac{x^{3+1}}{3+1} + C = frac{x^4}{4} + C $$

Теперь вводим неопределенный интеграл в онлайн калькулятор и сравниваем ответ.

Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!

Ответ

$$ int x^3 dx = frac{x^4}{4} + C $$

Пример 2

Найти неопределенный интеграл онлайн с помощью калькулятора и вручную. Сравнить полученные ответы: $$ int x sin x dx $$

Решение

Сначала решим сами, а затем в онлайн калькуляторе. Видим, что выражение под неопределенным интегралом представляет собой произведение двух простейших функций. Это значит можно применить формулу интегрирования по частям: $ int udv = uv — int vdu $

$$ int x sin x dx = begin{vmatrix} u = x & du = dx \ dv = sin x dx & v = -cos x end{vmatrix} = $$

$$ = -xcos x — int -cos x dx = -xcos x + sin x + C $$

Стоит заметить, что когда мы находили чему равно $ v $, то мы интегрировали функцию равенство $ dv = sin x $, то есть $ v = int sin x dx = -cos x $

Теперь вставляем в онлайн калькулятор неопределенный интеграл в формате: $ x*sin(x) $ и получаем ответ тот же, что и при ручном решении. Значит решение выполнено верно!

Ответ

$$ int xsin x dx = -x cos x + sin x + C $$

Найти неопределенный интеграл онлайн в калькуляторе не составляет никаких проблем. В ответе можно не сомневаться.

Источник

Неопределенным интегралом от заданной функции

называется множество всех её первообразных:

Для того чтобы вычислить неопределенный интеграл от некоторой функции необходимо использовать таблицу элементарных интегралов и правила интегрирования или воспользоваться нашим бесплатным онлайн сервисом.

Наш онлайн калькулятор способен найти подробное решение для очень многих типов интегралов. Решение, полученное у нас, содержит описание действий полностью на русском языке и соответствует стандартам образования, принятым в российских ВУЗах и учебных заведениях бывшего постсоветского пространства.

Со всеми преимуществами подробного решения Вы можете ознакомиться
здесь.
Посмотреть пример подробного решения можно
здесь.

Источник

Неопределенный интеграл онлайн

В школе говорят, интеграл – это значок ∫, а вычисление интеграла, то есть процесс интегрирования, – это операция обратная дифференцированию. Согласитесь скучно!

Разумеется, у школьников возникает резонный вопрос: а нафиг он нам нужен?

Но если бы учитель уделил несколько минут на вводную про интегралы, такой вопрос всё равно бы возник, но уже не у всех!

Вводная к интегралам

В далеком 17 веке были на тот момент нерешенные насущные проблемы, а именно изучались закономерности движения тел. Много трудов было проделано Ньютоном, чтобы понять, как вычисляется скорость тела в любой момент времени. Но чем дальше, тем оказалось интереснее.

Допустим, мы знаем закон изменения скорости тела – это некая функция. Тогда площадь фигуры, ограниченная этой кривой и осью координат, будет равна пройденному пути. Вычисляя неопределенный интеграл от функции, мы как раз находим общий закон движения.

В этом заключается один из физических смыслов интеграла.

Как вы уже поняли, геометрический смысл интеграла – это площадь криволинейной трапеции. Соответственно с помощью кратного интеграла вычисляется объем тела.

Решение интегралов

Лейбниц и Ньютон заложили основы дифференциального и интегрального исчисления. В последующие десятилетия было много великих открытий, связанных с вычислением интегралов.

Поскольку подынтегральная функция может принимать различные виды, естественно это привело к разделению интегралов на свои типы, а главное были отрыты многочисленные методы решения интегралов.

Но не все так безоблачно. На практике часто происходит так, что в аналитическом виде вычислить интегралы невозможно, то есть используя какой-либо известный метод. Конечно, получить аналитическое решение это здорово, но, с другой стороны, главное ведь вычислить точное значение интеграла. В этом случае интегралы решаются численными методами. Благодаря компьютерным мощностям, такие задачи не представляют особых сложностей для современного человека.

Калькулятор решения интегралов

Теперь самое интересное. Еще каких-то 15 лет назад школьник и помыслить не мог, что под рукой будут такие калькуляторы интегралов, как, например, наш. Это безусловно облегчает процесс обучения. Можно проверять свои решения, находить допущенные ошибки и лучше усваивать образовательный курс.

И тут в который раз повторяем, калькулятор решения интегралов – это только ваш безотказный помощник, к которому можете обратиться в любое время. Но никак не подмена вашей головы. Старайтесь самостоятельно решать задачи, только так можно развивать мышление, а компьютер будет в помощь.

Источник

bold{mathrm{Basic}}

bold{alphabetagamma}

bold{mathrm{ABGamma}}

bold{sincos}

bold{gedivrightarrow}

bold{overline{x}spacemathbb{C}forall}

bold{sumspaceintspaceproduct}

bold{begin{pmatrix}square&square\square&squareend{pmatrix}}

bold{H_{2}O}

square^{2}

x^{square}

sqrt{square}

nthroot[msquare]{square}

frac{msquare}{msquare}

log_{msquare}

theta

infty

int

frac{d}{dx}

ge	le	cdot	div	x^{circ}	(square)	\|square\|	(f:circ:g)	f(x)	ln	e^{square}
left(squareright)^{‘}	frac{partial}{partial x}	int_{msquare}^{msquare}	lim	sum	sin	cos	tan	cot	csc	sec

alpha	beta	gamma	delta	zeta	eta	theta	iota	kappa	lambda	mu
nu	xi	pi	rho	sigma	tau	upsilon	phi	chi	psi	omega

A	B	Gamma	Delta	E	Z	H	Theta	K	Lambda	M
N	Xi	Pi	P	Sigma	T	Upsilon	Phi	X	Psi	Omega

sin	cos	tan	cot	sec	csc	sinh	cosh	tanh	coth	sech
arcsin	arccos	arctan	arccot	arcsec	arccsc	arcsinh	arccosh	arctanh	arccoth	arcsech

begin{cases}square\squareend{cases}	begin{cases}square\square\squareend{cases}	=	ne	div	cdot	times	<	>	le	ge
(square)	[square]	▭:longdivision{▭}	times twostack{▭}{▭}	+ twostack{▭}{▭}	— twostack{▭}{▭}	square!	x^{circ}	rightarrow	lfloorsquarerfloor	lceilsquarerceil

overline{square}	vec{square}	in	forall	notin	exist	mathbb{R}	mathbb{C}	mathbb{N}	mathbb{Z}	emptyset
vee	wedge	neg	oplus	cap	cup	square^{c}	subset	subsete	superset	supersete

int	intint	intintint	int_{square}^{square}	int_{square}^{square}int_{square}^{square}	int_{square}^{square}int_{square}^{square}int_{square}^{square}	sum	prod
lim	lim _{xto infty }	lim _{xto 0+}	lim _{xto 0-}	frac{d}{dx}	frac{d^2}{dx^2}	left(squareright)^{‘}	left(squareright)^{»}	frac{partial}{partial x}

(2times2)	(2times3)	(3times3)	(3times2)	(4times2)	(4times3)	(4times4)	(3times4)	(2times4)	(5times5)
(1times2)	(1times3)	(1times4)	(1times5)	(1times6)	(2times1)	(3times1)	(4times1)	(5times1)	(6times1)	(7times1)

mathrm{Радианы}	mathrm{Степени}	square!	(	)	%	mathrm{очистить}
arcsin	sin	sqrt{square}	7	8	9	div
arccos	cos	ln	4	5	6	times
arctan	tan	log	1	2	3	—
pi	e	x^{square}	0	.	bold{=}	+

Подпишитесь, чтобы подтвердить свой ответ

Войдите, чтобы сохранять заметки

Войти

Номер Строки

Примеры

int e^xcos (x)dx
int cos^3(x)sin (x)dx
int frac{2x+1}{(x+5)^3}
int x^2ln(5x)
int frac{1}{x^2}dx
int frac{e^{2x}}{1+e^{2x}}
неполные:дроби:int_{0}^{1} frac{32}{x^{2}-64}dx
подстановка:intfrac{e^{x}}{e^{x}+e^{-x}}dx,:u=e^{x}
Показать больше

Описание

Поэтапное решение неопределенных интегралов

indefinite-integral-calculator

Блог-сообщения, имеющие отношение к Symbolab

Advanced Math Solutions – Integral Calculator, advanced trigonometric functions

In the previous post we covered substitution, but substitution is not always straightforward, for instance integrals…

Введите Задачу

Сохранить в блокнот!

Войти

Источник

Данный онлайн калькулятор позволяет найти неопределенный интеграл и получить ход решения.
Неопределенный интеграл — это множество первообразных функции f(x) называется неопределённым интегралом от этой функции и обозначается символом ∫f(x)dx.
Как следует из изложенного выше, если F(x) — некоторая первообразная функции f(x), то ∫f(x)dx = F(x)+C где C — произвольная постоянная.

Функцию f(x) принято называть подынтегральной функцией, произведение f(x) dx — подынтегральным выражением.

Свойства неопределённого интеграла, непосредственно следующие из определения:
1) d∫f(x)dx = ∫f(x)dx
2) ∫F'(x)dx = F(x)+C , или ∫dF(x)dx = F(x)+C

Для получения пошагового решение интеграла, в ответе необходимо нажать Step-by-step.

Основные функции

$x^{a}$ : x^a

модуль x: abs(x)

Интегралы

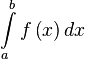Для того, чтобы найти неопределенный интеграл от функции f(x) нужно написать в строке: f[x], x. Найти определенный интеграл $intlimits_a^b {fleft( x right)dx}$ так же просто: f[x], {x, a, b} либо e f(x), x=a..b.