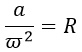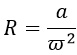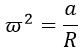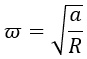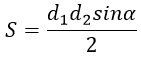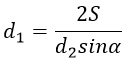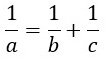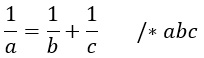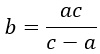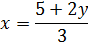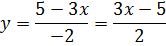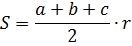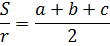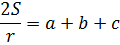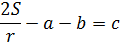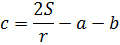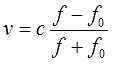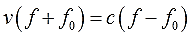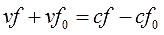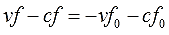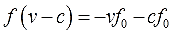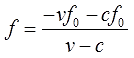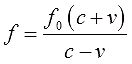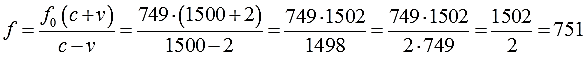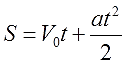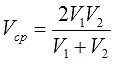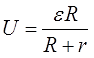Выведение переменной из формулы
Данную статью я начну с общего алгоритма выражения переменной, а затем уже будем разбираться на конкретных примерах.
Пусть дана какая-то формула…
1) Если она содержит скобки, то раскрываем их и приводим подобные слагаемые;
2) Если есть знаменатель, то избавляемся от него, умножив обе части формулы на этот знаменатель (если знаменателей несколько, то умножаем обе части равенства на общий знаменатель);
3) Если есть корни, то обе части возводим в степень, равную показателю корня;
4) Переносим все члены с нужной нам переменной в одну сторону;
5) Если таких членов несколько, то выносим нужную нам переменную за скобку в качестве общего множителя. Если нет, то этот шаг пропускаем.
6) Делим обе части формулы на все сомножители нужной нам переменной.
7) Если нужная переменная возведена в n-ую степень, то нужно из обеих частей формулы извлечь корень n-ой степени.
На самом деле, всё не так ужасно) На ОГЭ так вообще простые задания.
Вот парочка примеров.
1) Центростремительное ускорение при движении по окружности вычисляется по формуле a=ω2R, где ω — угловая скорость, R — радиус окружности. Выразим из этой формулы R и ω.
Выразим радиус R, разделив обе части на его сомножитель ω2:
Но обычно пишут так, чтобы искомая переменная была слева:
Теперь выразим угловую скорость. Разделим обе части равенства на сомножитель угловой скорости (на R, короче говоря):
Получается вот такая запись:
Нужная нам угловая скорость возведена в квадрат. Избавиться от степени нам поможет квадратный корень:
Теперь возьмем формулу с дробью.
2) Площадь четырехугольника можно вычислить по формуле
Выразим из нее d1.
Избавляемся от знаменателя, умножив обе части равенства на 2 (т.к. знаменатель равен двум).
Получим:
Чтобы выразить d1 разделим обе части на сомножители d2 и sinα.
Точно также выражаются d2 и sinα. Можешь даже самостоятельно попробовать.
Еще один пример. Последний.
3) Дана формула
Выразим из нее переменную b.
Формула содержит дроби, поэтому надо избавится от знаменателей. Умножим обе части равенства на общий знаменатель abc.
Получится такое выражение:
Перенесем все члены равенства, содержащие переменную b в левую часть.
Вынесем b за скобки как общий множитель.
Разделим обе части равенства на (с — а).
Что-то не выражается? Напиши мне свой пример. Используй функцию «Предложить новость».
https://vk.com/mymaths
Правила вывода величины из формулы
Формула – это правило вычисления одной величины через другие, записанное при помощи их буквенных обозначений.
Иногда для решения задач необходимо вывести неизвестную величину из формулы. Для этого существуют несколько правил.
Формулы можно преобразовывать по правилам математики. Рассмотрим примеры. В левой колонке таблицы вы видите исходные формулы. В средней колонке каждая из формул преобразована так, что «выражена» величина, обозначенная «b». В последней колонке выражена величина «с»
Примеры вывода физической величины из формулы
Физика
Тестирование онлайн
Учимся выражать
В каждой задаче по физике требуется из формулы выразить неизвестную, следующим шагом подставить численные значения и получить ответ. Лучше не решать физическую задачу по шагам: найти из одной формулы значение физической величины, затем подставлять ее во вторую формулу. Почему? Во-первых, получается неточный результат в вычислениях после многократного округления. Во-вторых, многие задачи нет возможности решить таким путем, из-за того, что нет значения некоторой физической величины. Но тупик часто заключается в том, что если бы мы подставляли в буквенном виде одну формулу в другую, то та неизвестная физическая величина сократилась бы. Поэтому учимся на примерах выражать из формулы необходимую физическую величину. Главное правило: букву, которую необходимо выразить, представляем в уме за x, остальные буквы представляем известными значениями. В этом случае получим совершенно обычное математическое уравнение.

Этот урок — полезное дополнение к предыдущей теме «Тождественные преобразования уравнений».
Умение делать такие вещи — штука не просто полезная, она — необходимая. Во всех разделах математики, от школьной до высшей. Да и в физике тоже. Именно по этой причине задания подобного рода обязательно присутствуют и в ЕГЭ и в ОГЭ. Во всех уровнях — как базовом, так и профильном.
Собственно, вся теоретическая часть подобных заданий представляет собой одну единственную фразу. Универсальную и простую до безобразия.
Удивляемся, но запоминаем:
Любое равенство с буквами, любая формула — это ТОЖЕ УРАВНЕНИЕ!
А где уравнение, там автоматически и тождественные преобразования уравнений. Вот и применяем их в удобном нам порядке и — готово дело.) Читали предыдущий урок? Нет? Однако… Тогда эта ссылочка — для вас.
Ах, вы в курсе? Отлично! Тогда применяем теоретические знания на практике.
Начнём с простого.
Как выразить одну переменную через другую?
Такая задача постоянно возникает при решении систем уравнений. Например, имеется равенство:
3x — 2y = 5
Здесь две переменные — икс и игрек.
Допустим, нас просят выразить x через y.
Что означает это задание? Оно означает, что мы должны получить некоторое равенство, где слева стоит чистый икс. В гордом одиночестве, безо всяких соседей и коэффициентов. А справа — что уж получится.
И как же нам получить такое равенство? Очень просто! С помощью всё тех же старых добрых тождественных преобразований! Вот и применяем их в удобном нам порядке, шаг за шагом добираясь до чистого икса.
Анализируем левую часть уравнения:
3x – 2y = 5
Здесь нам мешаются тройка перед иксом и —2y. Начнём с —2у, это попроще будет.
Перекидываем —2у из левой части в правую. Меняя минус на плюс, разумеется. Т.е. применяем первое тождественное преобразование:
3x = 5 + 2y
Полдела сделано. Осталась тройка перед иксом. Как от неё избавиться? Разделить обе части на эту самую тройку! Т.е. задействовать второе тождественное преобразование.
Вот и делим:
Вот и всё. Мы выразили икс через игрек. Слева — чистый икс, а справа — что уж получилось в результате «очищения» икса.
Можно было бы сначала поделить обе части на тройку, а затем — переносить. Но это привело бы к появлению дробей в процессе преобразований, что не очень удобно. А так, дробь появилась лишь в самом конце.
Напоминаю, что порядок преобразований никакой роли не играет. Как нам удобно, так и делаем. Самое главное — не порядок применения тождественных преобразований, а их правильность!
А можно из этого же равенства
3x – 2y = 5
выразить y через x?
А почему — нет? Можно! Всё то же самое, только на этот раз нас интересует слева чистый игрек. Вот и очищаем игрек от всего лишнего.
Первым делом избавляемся от выражения 3х. Перебрасываем его в правую часть:
–2y = 5 — 3x
Осталась двойка с минусом. Делим обе части на (-2):
И все дела.) Мы выразили y через х. Переходим к более серьёзным заданиям.
Как выразить переменную из формулы?
Не проблема! Точно так же! Если понимать, что любая формула — тоже уравнение.
Например, такое задание:
Из формулы
выразить переменную с.
Формула — тоже уравнение! Задание означает, что через преобразования из предложенной формулы нам надо получить какую-то новую формулу. В которой слева будет стоять чистая с, а справа — что уж получится, то и получится…
Однако… Как нам эту самую с вытаскивать-то?
Как-как… По шагам! Ясное дело, что выделить чистую с сразу невозможно: она в дроби сидит. А дробь умножается на r… Значит, первым делом очищаем выражение с буквой с, т.е. всю дробь целиком. Здесь можно поделить обе части формулы на r.
Получим:
Следующим шагом надо вытащить с из числителя дроби. Как? Легко! Избавимся от дроби. Нету дроби — нету и числителя.) Умножаем обе части формулы на 2:
Осталась элементарщина. Обеспечим справа букве с гордое одиночество. Для этого переменные a и b переносим влево:
Вот и всё, можно сказать. Осталось переписать равенство в привычном виде, слева направо и — ответ готов:
Это было несложное задание. А теперь задание на основе реального варианта ЕГЭ:
Локатор батискафа, равномерно погружающегося вертикально вниз, испускает ультразвуковые импульсы частотой 749 МГц. Скорость погружения батискафа вычисляется по формуле
где с = 1500 м/с — скорость звука в воде,
f0 — частота испускаемых импульсов (в МГц),
f — частота отражённого от дна сигнала, регистрируемая приёмником (в МГц).
Определите частоту отражённого сигнала в МГц, если скорость погружения батискафа равна 2 м/с.
«Многа букафф», да… Но буквы — это лирика, а общая суть всё равно та же самая. Первым делом надо выразить эту самую частоту отражённого сигнала (т.е. букву f) из предложенной нам формулы. Вот этим и займёмся. Смотрим на формулу:
Напрямую, естественно, букву f никак не выдернешь, она снова в дробь запрятана. Причём и в числитель и в знаменатель. Поэтому самым логичным шагом будет избавиться от дроби. А там — видно будет. Для этого применяем второе преобразование — умножаем обе части на знаменатель.
Получим:
А вот тут — очередные грабли. Прошу обратить внимание на скобки обеих частях! Частенько именно в этих самых скобочках и кроются ошибки в подобных заданиях. Точнее, не в самих скобочках, а в их отсутствии.)
Скобки слева означают, что буква v умножается на весь знаменатель целиком. А не на его отдельные кусочки…
Справа же, после умножения, дробь исчезла и остался одинокий числитель. Который, опять же, весь целиком умножается на буковку с. Что и выражается скобками в правой части.)
А вот теперь скобки и раскрыть можно:
Дальше дело нехитрое. Всё что с f собираем слева, а всё что без f — справа. Займёмся переносом:
Отлично. Процесс идёт.) Теперь буковка f слева стала общим множителем. Выносим её за скобки:
Осталось всего ничего. Делим обе части на скобку (v—c) и — дело в шляпе!
В принципе, всё готово. Переменная f уже выражена. Но можно дополнительно «причесать» полученное выражение — вынести f0 за скобку в числителе и сократить всю дробь на (-1), тем самым избавившись от лишних минусов:
Вот такое выражение. А вот теперь и числовые данные подставить можно. Получим:
Ответ: 751 МГц
Вот и всё. Надеюсь, общая идея понятна.
Делаем элементарные тождественные преобразования с целью уединить интересующую нас переменную. Главное здесь — не последовательность действий (она может быть любой), а их правильность.
В этих двух уроках рассматриваются лишь два базовых тождественных преобразования уравнений. Они работают всегда. На то они и базовые. Помимо этой парочки, существует ещё множество других преобразований, которые тоже будут тождественными, но не всегда, а лишь при определённых условиях.
Например, возведение обеих частей уравнения (или формулы) в квадрат (или наоборот, извлечение корня из обеих частей) будет тождественным преобразованием, если обе части уравнения заведомо неотрицательны.
Или, скажем, логарифмирование обеих частей уравнения будет тождественным преобразованием, если обе части заведомо положительны. И так далее…
Подобные преобразования будут рассматриваться в соответствующих темах.
А здесь и сейчас — примеры для тренировки по элементарным базовым преобразованиям.
Простенькая задачка:
Из формулы
выразить переменную а и найти её значение при S=300, V0=20, t=10.
Задачка посложнее:
Средняя скорость лыжника (в км/ч) на дистанции в два круга рассчитывается по формуле:
где V1 и V2 — средние скорости (в км/ч) на первом и втором кругах соответственно. Какова была средняя скорость лыжника на втором круге, если известно, что первый круг лыжник пробежал со скоростью 15 км/ч, а средняя скорость на всей дистанции оказалась равной 12 км/ч?
Задача на основе реального варианта ОГЭ:
Центростремительное ускорение при движении по окружности (в м/с2) можно вычислить по формуле a=ω2R, где ω — угловая скорость (в с-1), а R — радиус окружности. Пользуясь этой формулой, найдите радиус R (в метрах), если угловая скорость равна 8,5 с-1, а центростремительное ускорение равно 289 м/с2.
Задача на основе реального варианта профильного ЕГЭ:
К источнику с ЭДС ε=155 В и внутренним сопротивлением r=0,5 Ом хотят подключить нагрузку с сопротивлением R Ом. Напряжение на этой нагрузке, выражаемое в вольтах, даётся формулой:
При каком сопротивлении нагрузки напряжение на ней будет 150 В? Ответ выразите в омах.
Ответы (в беспорядке): 4; 15; 2; 10.
А уж где числа, километры в час, метры, омы — это как-нибудь сами…)
Как выразить величину из формулы
В физике величинами являются количественные характеристики предметов и показатели взаимодействий тел между собой и окружающей средой, например длина, масса, скорость, время, углы и проч. Эти параметры могут быть зависимыми или независимыми один от другого. Отношения многих связанных величин представлены в известных формулах, из которых всегда можно выразить любую переменную.

Инструкция
Выражение величины из формулы производится с помощью математических операций – переноса членов, деления на одно число обе части записи и др. То есть, следует упрощать и работать с формулой, как с алгебраическим уравнением. Выполняя данные действия, нужно также учитывать смену знака, правила вывода величины из под корня, возведения в степень.
В наиболее простом случае при наличии выражения вида v = 2*g + 11 для поиска величины g выполните следующие действия. Перенесите все члены, не содержащие переменную g в одну (лучше левую) часть данного уравнения, не забывая поменять их знак при переносе на противоположный: -2*g = 11 — v. Остальные величины и константы перенесите за знак равенства. Если при искомой величине стоит коэффициент, как в данном случае (-2), разделите на эту константу обе части уравнения: g = -(11 – v)/2.
При выражении из формулы величины, возведенной в степень, как, например, в следующем варианте: S = a*t²/4, выполните сначала выше описанные действия. Поставьте переменную в степени по левую сторону уравнения, причем для вывода константы из знаменателя дроби умножьте на это число обе части формулы: a*t² = 4*S. Поделите уравнение на переменную а и получится: t² = 4*S/а. Чтобы убрать степень искомой переменной, возьмите корень этой же степени (здесь квадратный) как с левой, так и с правой части выражения: t = √4*S/а. Встречается и обратная ситуация, когда искомая величина стоит под знаком корня, в этом случае требуется выполнить возведение всего уравнения в степень, указанную при корне. Так, выражение ³√S = v + g преобразуется в вид S = (v + g)³.
При наличии сложных выражений, полученных в результате многократных подстановок различных формул, часто возникают затруднения в выражении неизвестной величины. Например, в конструкции вида S = (√t²*k/(1+g))*f – 15 при поиске величины k желательно провести предварительное упрощение уравнения с помощью введения подстановочной переменной. Примите за х выражение в больших скобках: х = (√t²*k/(1+g)), тогда изначальное уравнение будет выглядеть так: S = х*f – 15. Отсюда легко находится х = (S + 15)/f. Далее верните вместо х скобочное выражение (√t²*k/(1+g)) = (S + 15)/f . После чего можно продолжать упрощения с помощью аналогичных подстановок или сразу выразить искомую величину: k = ((1+g)*(S + 15)/f )2/t².
Источники:
- выражение величин
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.